浊流对复杂构造地貌的水动力和沉积响应*

葛智渊 许鸿翔

1 中国石油大学（北京）地球科学学院，北京102249

2 油气资源与工程全国重点实验室，中国石油大学（北京），北京102249

1 概述

浊流（turbidity current）是水、泥、沙和各类陆缘碎屑等物质的混合物，其主要内在驱动力是沉积物颗粒与环境水之间的密度差，并以湍流支撑机制为主要特征，因而是一种典型的水下沉积物密度流（subaqueous sediment density flow；Kuenen，1937；Johnson，1939；Lowe，1982；Altinakaretal.，1996；Knelleretal.，1999；Mulder and Alexander，2001；Muttietal.，2009；Meiburg and Kneller，2010；Tallingetal.，2012）。单次浊流事件的持续时间从几分钟到几小时不等（Xu，2010；Xuetal.2014；Hughes Clarke，2016；Paulletal.，2018），更有甚者持续时间可长达数周（Azpiroz-Zabalaetal.，2017）。而且，单次浊流事件的流量可以数倍于全球河流的年径流量（Tallingetal.，2012，2022）。这样的快速搬运作用使浊流携带了大量陆源沉积物碎屑，经由海底峡谷进入数百甚至上千公里外的深水盆地之中，形成富含陆源有机物和营养物的海底扇（Tallingetal.，2013；李相博等，2013）。海底扇作为油气、矿藏、稀土等自然资源的潜在储集层，是地学界和工业界持续多年的研究重点（Kuenen and Migliorini 1950；Lowe，1982；庞雄等，2007；汪品先，2009；Tallingetal.2012；鲜本忠等，2014；龚承林等，2022；李华等，2023；田冬梅和姜涛，2023）。与此同时，浊流高达数米每秒甚至数十米每秒的流速（最大可达～19m／s，即～70 km／h）（Tallingetal.，2013）所带来的强大侵蚀力和破坏力，可对包括海底通信光缆、油气输送管道、隧道等在内的海底设施及钻井平台造成威胁。相关的海洋灾害研究也以浊流为重要的研究对象。

传统的浊流沉积模式往往考虑其在平坦深水区的沉积过程。但实际上，浊流所沉积的陆坡和各类构造盆地中往往具有复杂的地貌特征。在构造运动控制下的沉积盆地中，构造变形和不同构造单元间的组合形成了构造地貌。在这类盆地中，浊流沉积物的分布在整体和宏观上往往受到物源供给、构造活动、气候变化、海平面升降等因素的综合影响。但在局部和微观上，浊流的流动路径和沉积物分布主要受到构造地貌的控制（Gaw thorpe and Hurst，1993；Clark and Cartwright，2009）。因此，浊流对复杂构造地貌的响应越来越受到地学界和工业界的关注。

得益于大量的野外露头，数值模拟、物理模拟和近年来逐渐成熟的原位观测技术，浊流对地貌的水动力响应机制越来越明确。水槽实验揭示了浊流对地貌的水动力响应机制主要包括反射、偏转、水跃等，并在此过程中展现出不同的水动力和沉积特征。这些特征在野外露头、三维地震等资料上都得到了验证（Hiscott and Pickering，1984；Pantin and Leeder，1987；Garcia and Parker，1989；Edwardsetal.，1994；Clark and Cartw right，2009，2011，2012；How lettetal.，2021）。相比较而言，浊流对各类构造地貌的响应，尽管近年来取得了不少进展，但在细节上还有许多待完善的问题。这主要是由于构造地貌在三维上具有不断变化的特征，而多个类似构造形成的组合地貌又具有不同于单一构造地貌的复杂空间特点。例如，单个正断层在沿走向从断层中心到端点时，断层断距逐渐变小直至消失成为断层传播褶皱。但当2个同倾向的正断层互相影响时，则会形成以转换斜坡为代表的转换构造，影响浊流系统的运输与沉积（Geetal.，2017，2018）。

作者将以浊流对构造地貌的水动力响应机制为基础，梳理浊流对于褶皱、正断层、微盆地及坡折地貌响应的研究进展，总结当前的研究成果需要加强的方面，力图指明未来浊流对复杂构造地貌响应的研究可朝着定量化、真实化、构造—沉积耦合等方向发展。

2 浊流对地貌的水动力响应机制

浊流对地貌的水动力和沉积响应在微观上是浊流与不同三维坡度互相作用的结果。特别是对于浊流来说，由于其重力流的特性，沉积物重力势能在垂向上受到的坡度影响会直接影响浊流的流体状态和沉积物负载量。早期的浊流沉积模型以深水扇模型为主导（Normark，1970；Mutti and Ricci，1978），较少考虑复杂地貌对浊流沉积的影响。随着对浊流和其沉积物研究的不断深入，基于大量的野外露头（Hiscott and Pickering，1984；Pickering and Hiscott，1991；Clayton，1993；Haughton，1994；Greculadetal.，2003）、水槽实验（Alexander and Morris，1994；Edwardsetal.，1994；Amyetal.，2004；Abharietal.，2018；Farizanetal.，2019）、数值模拟（Nasr-Azadani and Meiburg，2014a，2014b；W ilsonetal.，2018；Goodarzietal.，2020）的研究，浊流对地貌的水动力响应机制越来越明确。从浊流的流体状态来说，当浊流遇到复杂地貌时，浊流可能会发生反射、偏转（发散型、汇聚型）甚至直接越过地貌于背流面发生水跃（图1）。从具体控制因素上来说，浊流对复杂构造地貌差异的水动力响应机制取决于浊流自身的特性（流速、流向、浓度、密度、厚度等）和地貌的几何形状及大小，并在此过程中展现出差异的水动力和沉积特征。

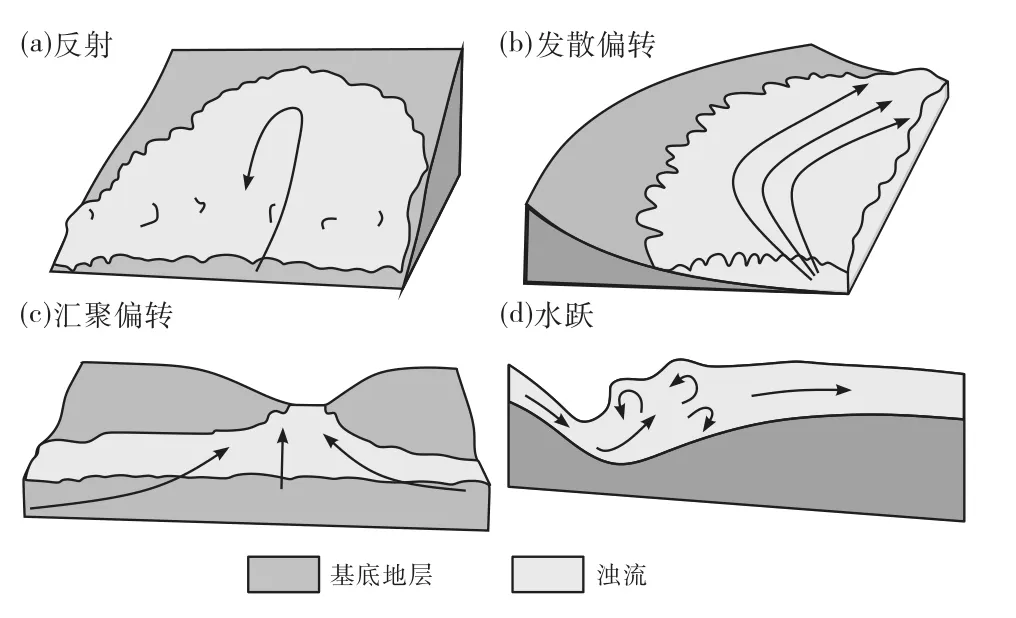
图1 浊流对复杂地貌的水动力响应机制模式（据Patacci et al.，2015；有修改）Fig.1 Hydrodynamic response model of turbidity current to complex topography（modified from Patacci et al.，2015）

由于水平面对浊流的重力势能变化基本无影响，因此在二维上，所有影响浊流能量的地貌都可被简化为2种：上坡与下坡。在不考虑侵蚀和沉积的简单情况下，浊流在流经上坡的过程中，重力势能增加、动能减少；在流经下坡的过程中，重力势能减少而动能增加。但从浊流的内部结构看，由于沉积物含量自下而上不断减少，因此地貌变化对浊流势能和动能的转换在浊流内部不同高度影响不同。如果考虑到浊流的沉积物本身也需要湍流作为支撑，其动能变化与沉积物含量也息息相关，流体水动力和沉积行为就更为复杂。因此，早期浊流对地貌的响应难以完全定量描述。直至Kneller和McCaffrey（1999）参考气象领域中气流对山体障碍物的研究，提出了利用内弗劳德数（Fri）判断浊流对障碍物响应的定量方法。其基本原理正是由于浊流内部分层，使得悬浮沉积物浓度在垂向上具一定的梯度，产生密度（浓度）和粒径分层（Stacey and Bowen，1988；Middleton，1993；Buckeeetal.，2009），且其底部常具高密度、高流速的基底 层（Hughes Clarke，2016；Paulletal.，2018；Popeetal.，2022）。构造地貌周围浊流的分层特征是浊流对于构造地貌具有复杂响应的关键所在，常用无量纲的参数——内弗劳德数（Fri）表征，其取决于流速、流体厚度和密度分层程度的倒数，计算方程如下（Kneller and McCaffrey，1999）：

式中：ρ为参考密度，此处为浊流周围环境水的密度。

低内弗劳德数会导致迎流面流体解耦形成一个分界流线（面），将流体分隔为2个部分：分界流线之下高沉积物浓度流体由于密度更高和距离地貌顶部较远，使得其所具有的动能不足以支撑流体上升至地貌顶部，转而在地貌周围偏转绕过；而分界流线之上的低沉积物浓度流体如具有足够的动能转化为重力势能，则可直接越过地貌起伏，如因动能不足则反射回流。分界流线高度hs计算方程如下（Kneller and McCaffrey，1999）：

式中：H为地貌高度；θ为地貌形状系数，取值范围为0.7～2.0，默认值为1（Baines，1979；Hunt and Snyder，1980；Snyderetal.，1985；Goodarzietal.，2020）。

依据伯努利原理（A llen，2012），流体遭遇地貌之后动能减少量与最大爬升高度（hmax）处流体的重力势能增加量相当，满足如下能量守恒公式：

对于分层明显流体，考虑垂向上流体密度的非均一性，其能量守恒公式如下（Muck and Underwood，1990；Kneller and McCaffrey，1999；Allen，2012）：

式中：uz为初始高度z处流体垂直于地貌方向的速度分量；ρz为初始高度z处流体的密度；ρz为初始高度z处流体与环境水之间的密度差；Eloss为摩擦能量损失率。

因此，从定量分析的角度，迎流面流体对于复杂地貌的差异响应受到分界流线高度hs、最大爬升高度hmax和地貌高度H的复合控制（Kneller and McCaffrey，1999）。hs小于0（Fri＞1／θ）时，流体内部不存在分界流线：若hmax＞H，则浊流具有足够多的动能克服重力在地貌起伏高度上做的功，整体直接向上越过地貌起伏；若hmax＜H，则浊流整体因动能不足在重力作用下反射回流，形成一系列的反射内波。hs大于0（Fri＜1／θ）时，流体内部存在分界流线：若hmax＞H，分界流线之下高浓度流体由于动能不足以支撑流体上升至地貌顶部，从而在周围偏转绕过地貌高点继续沿坡向下游流动，而分界流线之上低浓度流体因最大爬升高度大于地貌高度得以越过地貌起伏；若hmax＜H，分界流线之下高浓度流体同样在地貌周围偏转绕过，而分界流线之上低浓度流体沿着地貌起伏向上爬升，但因最大爬升高度小于地貌高度而最终反射回流至母流之中（图2，Kneller and McCaffrey，1999）。值得说明的是，hmax是浊流速度和密度剖面的复合函数，不可简单地一概而论。由于浊流在自然界是三维流体，具有很大的内部差异。因此，在同一次浊流事件中，垂向不同高度上和横向不同范围内，浊流的最大爬升高度可能具有较大的差异，从而同时导致部分流体hmax＞H，越过地貌起伏，而余下流体hmax＜H，反射回流至母流，此过程亦称为流体剥离（flow stripping）（Piper and Normark，1983）。此外，当地貌高度为流体厚度5倍以上时，无论浊流内部是否存在分界流线（Fri＞1／θ或Fri＜1／θ），流体皆被地貌完全封堵，流头高度最高可上升至流体厚度的4～5倍（Simpson，1982；Lane-Serffetal.，1995）。其中，当地貌起伏的高度大于流体厚度的2.5倍或流头厚度的1.5倍（Rottmanetal.，1985；Muck and Underwood，1990）时，地貌对浊流起到部分封堵作用，使其主体无法越过地貌（图2）。

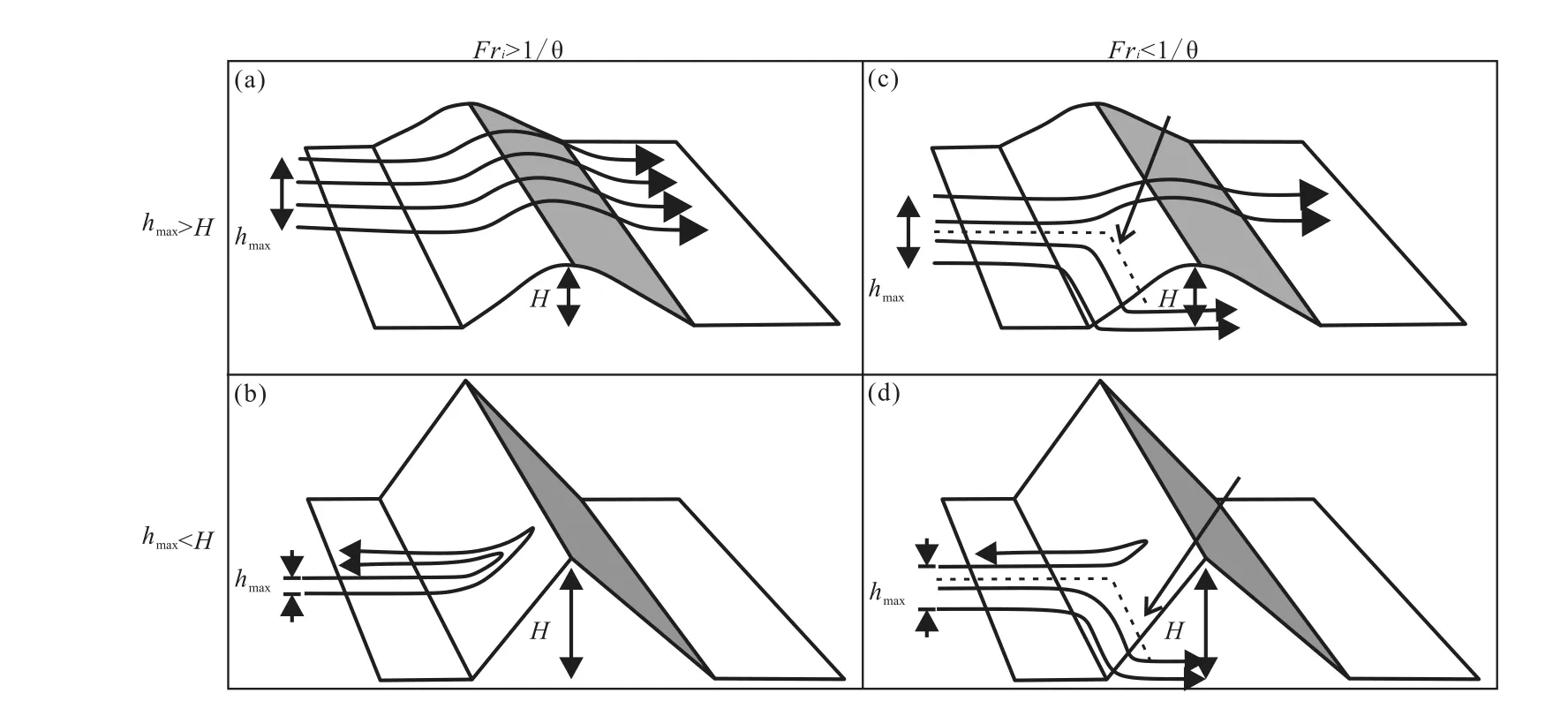
图2 分界流线（Fri）和限定程度（hmax／H）复合控制示意图（据Kneller and McCaffrey，1999；有修改）Fig.2 Schematic illustration of the joint controls of the dividing stream line（Fri）and the degree of confinement（hmax／H）（modified from Kneller and McCaffrey，1999）

越过地貌高点来到其背面的流体对于地貌的响应同样受到内弗劳德数的控制（图3）：（1）当流速足够大、微小地貌对浊流的影响微乎其微时，背流面流体Fri≫1／θ、未发生流体解耦，一体化的浊流流线在地貌起伏之上上凸后迅速下降、恢复至遭遇地貌之前的稳定状态，未产生更多的湍流扰动和阻塞效应（Long，1955）；（2）当背流面流体在越过类似于波纹、沙丘等小规模构造地貌时，Fri值开始低于1／θ，发生流体解耦现象，上部流体流线上凸后下降恢复稳定状态，而下部流体在流体内部密度梯度和地貌引起的重力加速作用下产生湍流扰动（Lawrence，1993）。随着Fri的减小，背流面下部流体的湍流耗散和混合作用将更加强烈（W inters and Arm i，2012）；（3）当地貌高度和流体密度梯度增大而流速继续降低时，背流面流体Fri进一步减小，在越过地貌背流面时在顺坡加速作用下转变为超临界流，随后在地貌下游方向产生一系列不断破碎的背流波（Castro and Snyder，1993），背流波具有与地貌相似的外形，其波长是Fri的函数（Miles and Huppert，1968），但所引起的巨大湍流扰动可能远高于地貌的高度；（4）当Fri达到最低值时，背流面顺坡加速下的超临界流体在坡脚地貌坡度急剧变化下，浊流内部发生水跃，地貌下游方向流体急剧减速、增厚，转变为亚临界流体。顺坡加速过程中重力势能转化为流体动能，随后水跃过程中动能又迅速转变为湍流的动能的耗散以及流体液面升高的重力势能（图3）。

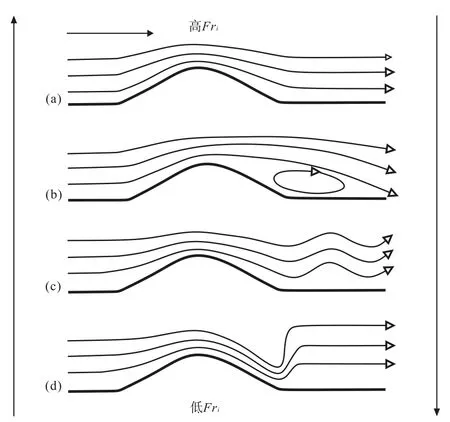
图3 内弗劳德数（Fri）对地貌下游流体的影响（据Kneller and Buckee，2000）Fig.3 Effect of internal Froude number（Fri）on the behavior of flows downstream of topography（after Kneller and Buckee，2000）

尽管地学界在浊流对地貌的水动力响应问题上已有较为完善的定量分析方法，但在实际工作中，由于直接观测浊流沉积的难度较高，对浊积岩的研究往往依赖于露头和岩心的解释。因此，把浊流在构造地貌下的水动力过程和沉积产物联系起来极为重要。这方面的研究主要基于水槽物理模拟和浊积岩的沉积过程推测。其中，主要的浊流响应过程包括：反射、偏转和水跃。

2.1 反射

在浊流反射中，与浊流沉积相关的沉积构造呈现出部分或完整的鲍玛序列Ta-e，表明沉积物来源于时空上能量逐渐减弱（速度逐渐减小）的单向流。Hiscott和Pickering（1984）在加大阿巴拉契亚山脉奥陶系盆地的深水平原野外露头中，通过槽模、爬升波纹交错层理、波痕等沉积构造所指示古水流方向的多次改变和递变层理的突然反转，首次识别出具有浊流反射过程的鲍玛序列。反射浊流具有与单向浊流相似的流动特征，在流速快速变化所导致沉积过程中产生相似但具组合特征的沉积序列。以此为标准，随后在达尔马提亚的新近系复理石（Marjanac，1990）、南设得兰群岛海沟（Porebskietal.，1991）、南海海槽（Pickeringetal.，1992）、马德拉深海平原（Rothwelletal.，1992）和亚平宁山脉北部（Tinterri and Tagliaferri，2015；Tinterri and Piazza，2019）等新近系、第四系浊积岩中均识别出浊流区域／局部反射的证据（图4；Hiscott and Pickering，1984；Pickering and Hiscott，1991）。

图4 加大阿巴拉契亚山脉奥陶系盆地的深水平原反射浊流野外露头与沉积模式（据Hiscott and Pickering，1984；有修改）Fig.4 Field outcrop and deposition model of reflected turbidity current on an Ordovician basin floor，Canadian Appalachians（modified from Hiscott and Pickering，1984）

基于大量浊流反射的野外露头证据，一系列水槽实验揭示了浊流反射的机制（Pantin and Leeder，1987；Edwardsetal.，1994）。浊流一经释放，在抵达斜坡前呈现出流头、主体和流尾的典型三段式分布。之后，浊流在斜坡处发生反射，流头由斜坡向上移动并迅速减速、变薄，浊流的主体同样减薄。同时，在流体下部可见远离斜坡的膨胀流体反向流动。流体的膨胀来源于反向流体流头的重力垮塌作用，使其裹挟顺向流体流尾并夹带悬浮沉积物。随后，膨胀的反向流体不断分解成一系列向上游迁移的内波（图5）。

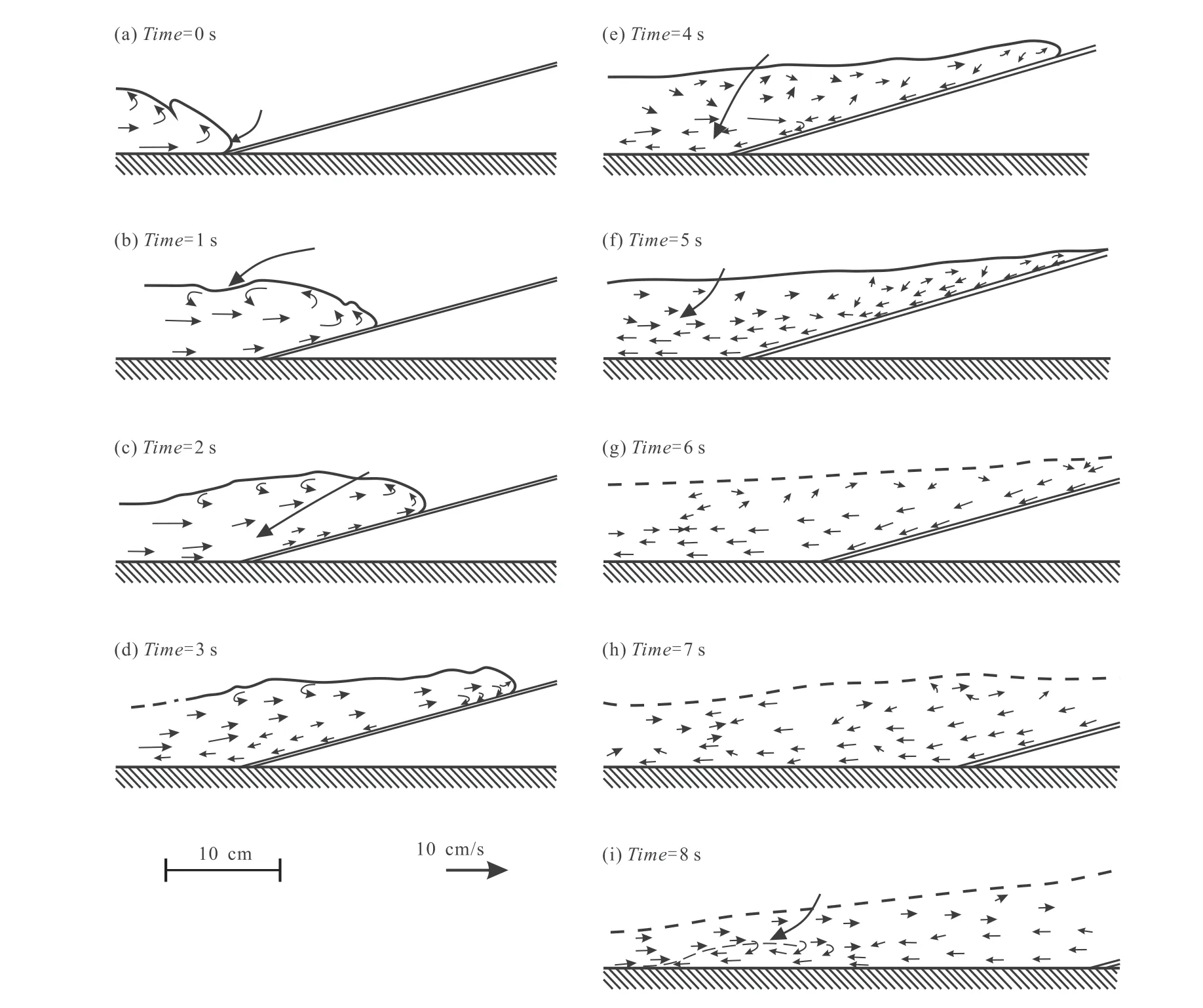
图5 水槽实验中浊流反射的内部流体运动示意图（据Edwards et al.，1994）Fig.5 Schematic diagram of internal fluid motions of reflected turbidity current during flume experiment（after Edwards et al.，1994）

无论浊流与反射面之间入射角的大小关系（垂直／倾斜入射），内波始终沿着反射面（斜坡）的垂直方向传播（Knelleretal.，1991；Edwardsetal.，1994；Kneller，1995）。在这一过程中，反射内波可以理解为浊流反射所形成的反向移动内部水跃：水跃过程中，流体厚度的突然增大伴随着流速的急剧减小，使原顺向流体的动能转化为水跃处的湍流动能、流体厚度增大所增加的重力势能以及反向传播的内波动能，在此过程中浊流的整体流态由超临界态转变为亚临界态。

反向流的速度Ub和流动距离dD（drag distance）计算方程如下（Pantin and Leeder，1987）：

式中：h为顺向流流尾的厚度；H为反向流的厚度；L为反向流的长度；g′为折算重力加速度，g［Δρ／ρa］；为流体上下界面的复合阻力系数；为与流头形状和大小相关的形状阻力系数。

因此，反向流的速度与厚度这二者和顺向流流尾厚度的比值呈正相关关系。浊流的反射除了由水跃形成上部的反射内波之外，在浊流减速、增厚使底部悬浮物浓度增加，并最终在形成的逆压梯度下，近底床区域出现流体边界层分离，地貌迎流面坡脚处会形成逆流而上的马蹄涡（horseshoe vortex）。对于由湍流支撑的、具高雷诺数的浊流，其反射内波移动距离大于马蹄涡的长度（Mignot and Riviere，2010；Nasr-Azadani and Meiburg，2014a；Geetal.，2017）。整体上，反射内波和马蹄涡的能量逐渐减弱，所运输的悬浮沉积物粒径逐渐变细，并形成与低底床剪切应力相关，并经过多次后期改造的底形（爬升波纹交错层理、波痕等），多次反射内波之间以细粒悬浮物沉降所形成的泥盖层所分隔（Edwardsetal.，1994；Tinterri and Tagliaferri，2015；Tinterri and Piazza，2019）。

2.2 偏转

偏转指浊流在流经地貌起伏时，流体的速度和方向随着流动距离的增加而不断变化以绕过地貌继续向下游方向流动的过程，其间浊流整体流动方向未发生180°的转变。

浊流的偏转涉及到浊流流体的稳定性和均匀性问题。其中，稳定流指流体连续通过空间中固定点具有相同的速度矢量，流体的流动随时间变化保持不变，即∂u／∂t＝0。与此相对应的是不稳定流：渐强流流速随时间变化逐渐增大，即∂u／∂t＞0；渐弱流流速随时间变化逐渐减小，即∂u／∂t＜0。均匀流指流体某一时间点连续通过空间中多个固定点具有相同的速度矢量，流体的流动随空间变化保持不变，即u·∂u／∂x＝0。与此相对应的是非均匀流：汇聚流流速随空间变化逐渐增大，即u·∂u／∂x＞0；发散流流速随空间变化逐渐减小，即u·∂u／∂x＜0（图6；Kneller，1995；Kneller and Branney，1995）。流体流动的净加速度计算方程如下：

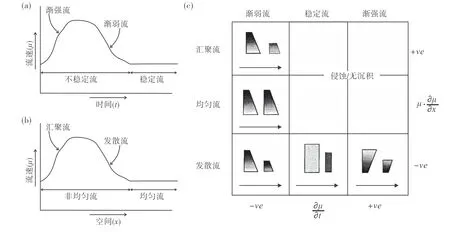
图6 稳定流／不稳定流和均匀流／非均匀流的定义草图和加速度矩阵（据Kneller，1995；有修改）Fig.6 Definition sketches and acceleration matrix for steady／unsteady flows and uniform／non-uniform flows（modified from Kneller，1995）

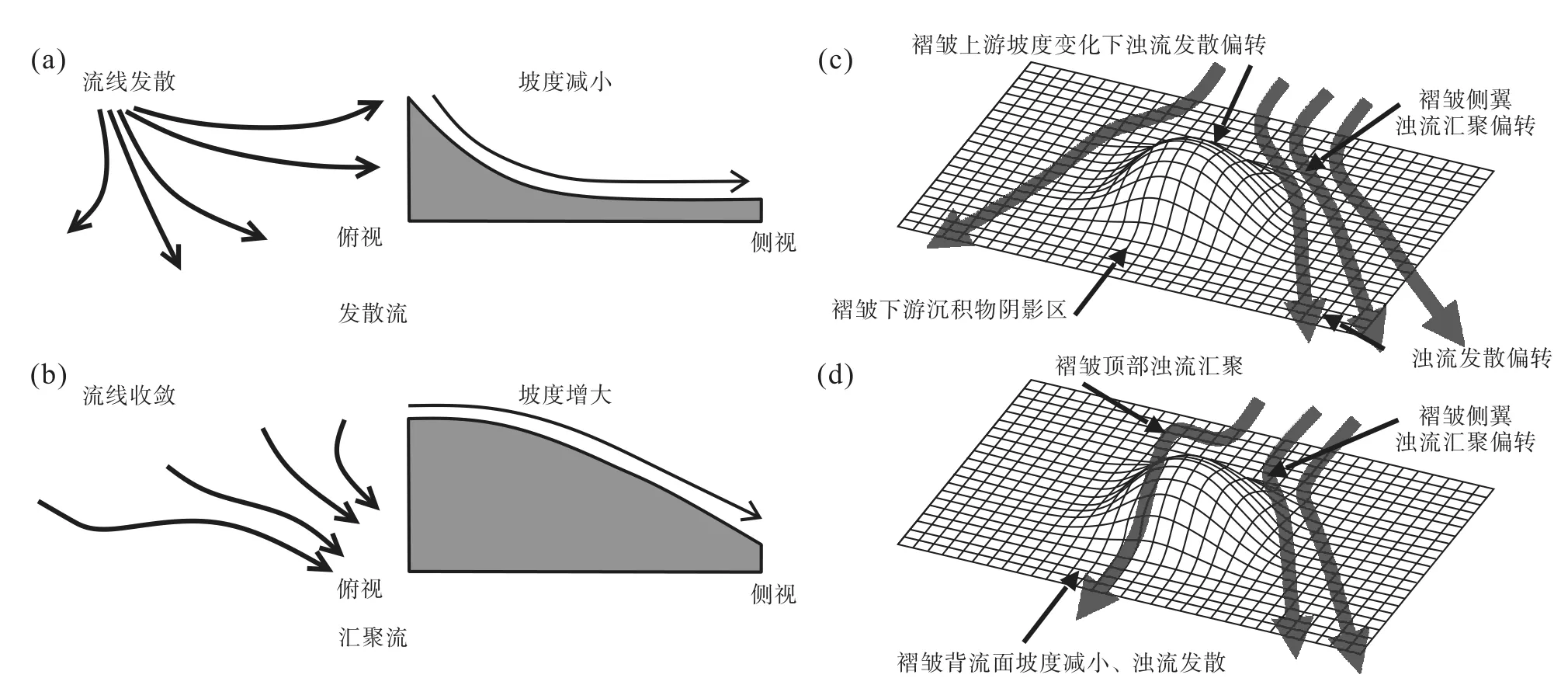
图7 产生发散流／汇聚流的情况（据Kneller and McCaffrey，1993；Kneller，1995；有修改）Fig.7 Situations producing divergent／convergent flows（modified from Kneller and McCaffrey，1993；Kneller，1995）

式中：∂u／∂t为浊流的时间加速度；u·∂u／∂x为浊流的空间加速度。

无论流体是稳定流／渐强流／渐弱流还是均匀流／汇聚流／发散流，其内悬浮物是否沉积的关键在于净加速度du／dt是否小于0。当du／dt＜0，在该时间点之后／空间点下游方向的时间点和空间点，流体的平均流速将开始低于最大颗粒的悬浮阈值，换言之湍流的动能无法继续支撑悬移质，沉积物总量超过流体的携带能力的上限，致使粒径大于粉砂的砂质和聚集成团的泥质由悬移质转变为推移质。直至后续流速小于推移质载荷的阈值，发生快速沉积。因此，净加速度du／dt是沉积是否发生的主要控制因素，但同时沉积物粒径垂向和横向变化将取决于流体不稳定性（时间加速度，∂u／∂t）和非均匀性（空间加速度，u·∂u／∂x）的正负和相对大小（图6；Kneller，1995）。

根据浊流偏转过程中流速随空间的变化（发散流／汇聚流），可划分为发散偏转和汇聚偏转。发散偏转过程中，浊流的空间加速度小于0，进一步细分可以发现：发散渐弱流和发散稳定流的净加速度一定小于0；而部分情况下，发散渐强流的净加速度也会小于0。因此，发散偏转整体上使浊流减速并沉积，主要发生于地貌坡度变缓处，如峡谷／水道出口的水道—朵叶过渡带、构造地貌迎流面的坡脚周围等。汇聚偏转过程中，浊流的空间加速度大于0，进一步细分：汇聚渐强流和汇聚稳定流的净加速度一定大于0；只有部分情况下，汇聚渐弱流的净加速度会小于0。因此，汇聚偏转整体上使浊流加速并侵蚀或过路，主要发生于地貌坡度变陡处，如构造地貌背流面、段边界的迎流面处、下伏塑性地层（盐岩／泥岩）的活动所形成的微盆地内等（图 6，图 7；Kneller and McCaffrey，1993；Kneller，1995）。

2.3 水跃

浊流中的水跃是指高流速的超临界浊流进入低流速或基本静止的亚临界环境水中，浊流流速急剧降低、厚度迅速增大，部分动能被湍流耗散或转换成重力势能使流体液面升高的水力跃迁现象（Komar，1971）。水跃是浊流对于地貌坡度剧变化的局部响应，导致地貌突变处湍流增强、侵蚀下切能力增加；同时水跃下游方向亚临界流体的剪切流速降低，悬浮物不断沉降、堆积，沉积区不断向上游方向扩张，水跃区域向上游方向迁移（图8）。因此，在悬浮物沉降的迟滞效应下，在水跃下游方向，浊流底床剪切速率与悬浮颗粒沉降速率比值U*／Us的减小，水跃下游方向沉积物堆积厚度不断增大，沉积物堆积区域往往位于水跃下游的一定距离内（Garcia and Parker，1989；Kostic and Parker，2006，2007；Postma and Cartigny，2014；Pohl，2019）。

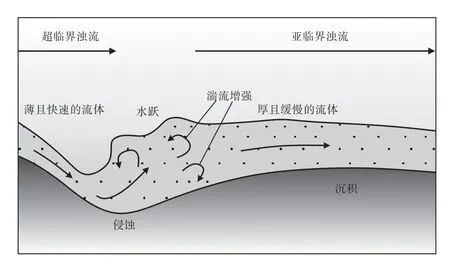
图8 浊流水力跃迁原理（据Postma and Cartigny，2014；Pohl，2019；有修改）Fig.8 Schematic diagram of a hydraulic jump of turbidity current（modified from Postma and Cartigny，2014；Pohl，2019）

3 浊流对构造地貌的响应

本质上，浊流对复杂地貌差异响应的微观机制决定了其对构造地貌的宏观响应。因此，浊流对地貌响应的微观机制研究能从理论上推导出宏观状态下的浊流沉积特征。然而，从微观机制到宏观沉积特征的定量描述依赖于较为完整的浊流水动力信息，包括但不限于浊流的速度、沉积物浓度和分布等参数。这对绝大多数浊流沉积物都是无法获得的参数，因形成浊积岩的流体已消逝而无法测量。同时，由于构造地貌过于复杂，单一浊流系统对单个构造地貌的响应通常已经包括了反射、偏转和水跃。当第2个类似或不同的构造出现时，浊流的水动力条件可能发生局部甚至大部分改变，从而调节沉积物的分布特征。因此，针对浊流对构造地貌的响应，目前的研究方式依然以较为简单的构造和沉积参数为前提，并在研究实例的基础上，构建特定地貌下具有代表性特征的浊流沉积模型。文中详述的构造地貌重点集中于挤压构造背景下产生的褶皱，拉张背景下产生的正断层，盐构造区域常见的微盆地和陆架边缘常见的坡折带。浊流对其他构造地貌的响应，一方面未见较为详细的定量研究，另一方面也能够在这些典型的构造区域找到相类似的地貌。例如，走滑断层形成的正花状凸起和负花状凹陷，在地貌上部分类似于褶皱突起和微盆凹陷。

3.1 浊流对褶皱地貌的响应

作为深水区最为典型的正地形，由逆冲断层、盐／泥底辟构造引起的褶皱地貌广泛分布于婆罗洲西北缘褶皱冲断带、尼日尔三角洲盆地、西非／巴西外海／墨西哥湾等被动大陆边缘盆地（Heiniöand Davies，2006；Morley，2007，2009；Morley and Leong，2008；Hesseetal.，2010；Mayalletal.，2010；Morleyetal.，2011；Oluboyoetal.，2014；赵晓明等，2018；How lettetal.，2021；Zhangetal.，2021）；褶皱所形成的正地形遮挡及其附近局部的负地形限定，直接影响了浊流（水道）的流动路径和相关沉积中心的形成，进而控制了沉积物分布模式。

流体动力学数值模拟研究揭示了非限定性浊流垂直流向不同规模褶皱构造的水动力响应过程和沉积物分布特征：浊流在褶皱后缘的反向斜坡上发生反射回流（逆流水跃）而减速、增厚，上部浊流反射形成稀疏的反向溢流，同时底部高密度沉积物负载下形成致密的反向底流。浊流的回流携带沉积物颗粒重新汇入母流之中，降低了母流的衰减速率，延长了母流的持续时间。大部分浊流沿着褶皱后缘发散偏转，并在绕过褶皱侧翼后继续顺坡而下输送沉积物；流体上部小部分低浓度浊流溢出褶皱，在褶皱前缘的坡脚处发生水跃并堆积沉积物。褶皱构造地貌下浊流所携带的沉积物主要分布于褶皱后缘和前缘2处沉积物堆积区（图9；How lettetal.，2019）。褶皱大小在很大程度上决定了浊流对褶皱地貌的差异响应：对于小型褶皱，浊流迅速包围整个褶皱区域，轴向部分流体减速增厚、膨胀，整体足以溢出至褶皱前缘并发生水跃；对于大型褶皱，浊流主要在褶皱后缘偏转绕过褶皱区域，只有少部分低浓度流体溢出至褶皱前缘并发生水跃，并在褶皱前缘形成沉积物堆积缺失的 “阴影区”（How lettetal.，2019）。此外，褶皱的遮挡使得浊流在褶皱后缘反向斜坡上膨胀减速、反射回流，往往还伴随着混合事件层（hybrid event beds）的形成（Tinterri and Tagliaferri，2015；操应长等，2017a；Tinterri and Piazza，2019）。浊流对褶皱的响应广泛分布于全球深水区。如婆罗洲西北缘褶皱冲断带之上发育的大型非限定性浊积扇，其在下伏不断生长的多段逆冲断层的持续作用下，沉积物分布明显受到逆冲褶皱的控制，广泛分布于褶皱侧翼和褶皱之间的背驮式盆地（图10；Morley，2007；Morley and Leong，2008；Morley，2009）。此 外，自然界浊流对褶皱的响应除了大型的非限定性浊积扇，还包括不同规模的水道—朵叶复合体。褶皱地貌对于水道—朵叶复合体的控制方式包括：限制（confinement）、改向（diversion）、偏转（deflection）和封堵（blocking）（图11；Clark and Cartwright，2009，2011，2012；陈亮等，2017）。上述4种响应模式体现出在重力和微观机制驱动下，浊流侵蚀及沉积作用形成的水道—朵叶复合体流动路径总是遵循湍流动能损失最小（正地形最低处）和重力势能减小最大（负地形最低处）的规律。在褶皱构造持续生长作用下，浊流对于褶皱的响应还体现在水道—朵叶复合体的长期演化：如尼日尔三角洲盆地距今15～3.7Ma逆冲断层侧向连接、生长、成熟和衰亡的长期演化过程中，水道—朵叶复合体先后经历了天然堤限定、垂向加积的沉积型单一水道→天然堤限定、侧向叠置的侵蚀型复合水道和局限性朵叶→水道化席状朵叶等多个阶段（图12；Pizzietal.，2020，2021，2023）。

图10 边缘检测属性图、RMS振幅属性图和区域地震剖面，示意了婆罗洲西北缘褶皱冲断带的主要构造和沉积特征（据Morley，2009；有修改）Fig.10 Edge map，RMS amplitude map of the seafloor and regional seismic lines，illustrating the main structural and sedimentary features of fold and thrust belt，NW margin of Borneo（modified from Morley，2009）

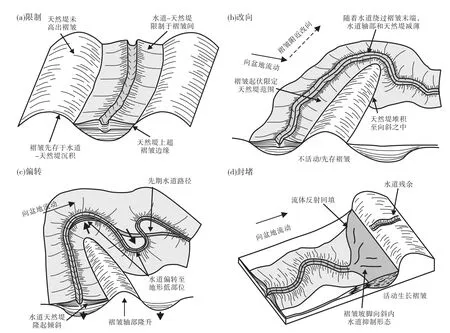
图11 海底水道发育与褶皱地形相互作用的概念模型（据Clark and Cartw right，2009，2011）Fig.11 Conceptualmodels of interactions between submarine channel development and fold topography（after Clark and Cartwright，2009，2011）

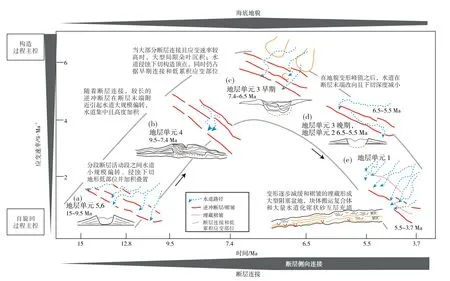
图12 应变率和断层连接随时间变化下，水道路径和构型的持续变化模式（据Pizzi et al.，2023）Fig.12 Synthetic diagram summarizing the key changes in channel pathways and architectures as a function of strain rate and fault linkage through time（after Pizzi et al.，2023）

在此基础之上，褶皱与浊积水道之间相互作用的控制因素更是近年来的研究热点。具体而言包括：构造上，褶皱的规模及外部形态特征；沉积上，浊积水道的规模、弯曲度、是否发育天然堤等。此外，褶皱构造的生长速率与浊积水道内部沉积物堆积速率的相对大小也极其重要：当褶皱生长速率大于浊流沉积速率时，根据褶皱形成的不同构造地貌，水道可能发生高角度改向、向褶皱段边界改向、向下游可容空间发生改向；朵叶受控于褶皱地形起伏的单侧／双侧限制作用阻塞了浊流沿斜坡而下的路线，形成局限性朵叶。当褶皱生长速率小于浊流沉积速率时，水道会绕过褶皱发生小角度（小规模）的改向；同时褶皱也不会对朵叶起到封堵及局限作用，其远端朵叶会不断叠置发育（图13；Oluboyoetal.，2014；Howlettetal.，2021）。此外，水槽模拟研究证实了浊流流向与褶皱走向之间的夹角在很大程度上决定了两者相互作用的方式、浊流的流态及其对浊流沉积的控制：浊流流向与褶皱走向近于平行时，褶皱单侧限制浊流的同时，浊流会侵蚀侧向褶皱遮挡物，轴向流速显著加快；浊流流向与褶皱走向斜交时，部分浊流沿着斜向褶皱发生偏转并加速，导致浊流在褶皱周围发生分叉，形成褶皱前缘及后缘浊流转向处2个主要沉积区；浊流近乎垂直流向褶皱时，褶皱正面直接限制浊流，部分浊流直接侵蚀、越过褶皱，在褶皱的前缘部位发生水跃与沉积，部分浊流受到褶皱的封堵作用，在褶皱后缘处发生反射回流分散并产生沉积物的堆积（Soutteretal.，2021）。

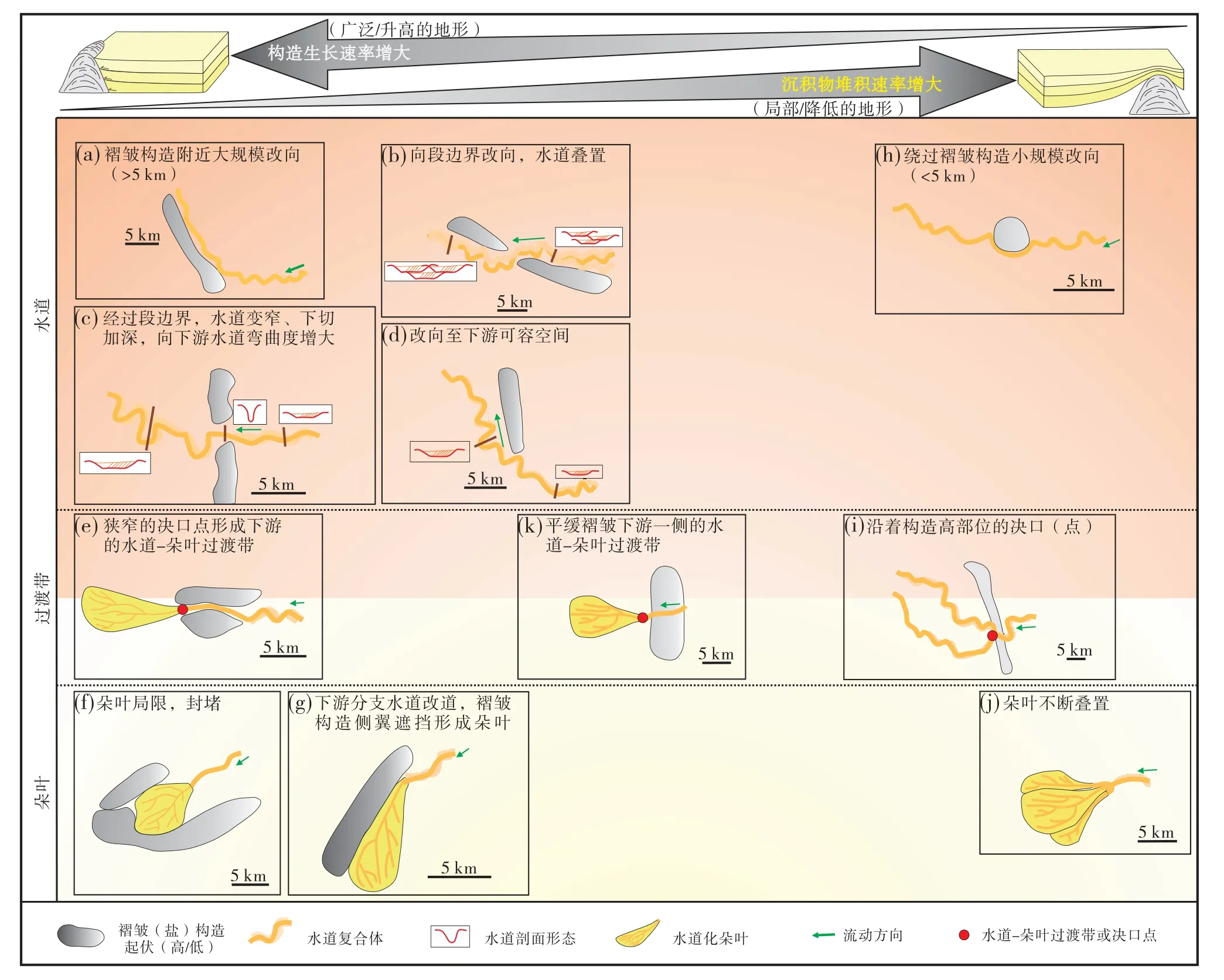
图13 盐底辟等盐核构造对深水沉积体系的主要影响总结图（据Howlett et al.，2021）Fig.13 Summary graph of the major influences of salt-cored structures such as salt diapirs on deep-water depositional systems（after Howlett et al.，2021）

水道形态演化对于褶皱生长响应的定量研究是近年来的另一研究热点。Jolly等先后对尼日尔三角洲褶皱冲断带的多个研究区采用定量方法恢复下伏逆冲褶皱构造的应变（率）和累积应变（率），同时对水道剖面形态（宽度、深度、宽深比、凹度等），平面形态（蛇曲度、曲率），满槽水力学参数预测（底床剪切应力、流速等）等进行统计学定量分析（Jollyetal.，2016，2017；Pizzietal.，2021；Mitchelletal.，2021a，2021b，2022）。相关研究成果揭示了浊流总是选取构造应变（率）最低处（即褶皱隆起相对最低点）侵蚀下切，在水道剖面形态上表现为下切深度显著增大，但水道宽度无明显变化，宽深比显著减小，水力学参数计算所预测的底床剪切应力和浊流流速显著增大；当底床剪切应力未达到阈值时，在生长褶皱的地形起伏作用下，水道发生改向或偏转，蛇曲度、曲率增大，且水道内部浊流更容易溢出天然堤形成决口扇。

尽管在主要的沉积模式上取得了相当的进展，当前浊流对褶皱的响应研究仍然存在一些不足之处。首先，水道能否下切褶皱的底床剪切应力与构造应变率之间相互的阈值及相关参数的控制作用仍不明确，亟需更多基于高精度海底测深数据的统计学定量研究。其次，受限于盐岩活动的多期性及复杂性，广泛分布于被动大陆边缘盐相关褶皱的生长速率恢复仍是构造地质学家们面临的棘手问题（Giles and Rowan，2012；Cumberpatchetal.，2021a，2021b）。同时，浊流对多期、持续性生长盐相关褶皱和底辟的响应仍不明确，缺乏水道形态演化与盐构造生长速率恢复的定量研究。最后，自然界中的褶皱带往往由多段褶皱所构成，褶皱之间的排列方式及连接方式具有时间和空间上的差异性与复杂性（图 10；Higginsetal.，2007；Morley，2009；Bretisetal.，2011；Grasemann and Schmalholz，2012；Fernandez and Kaus，2014；Collignonetal.，2014，2015）。但当前的定量研究往往局限于单一褶皱（图13；How lettetal.，2019；Soutteretal.，2021），缺乏浊流对多段褶皱地貌水动力和沉积响应的定量研究。

3.2 浊流对正断层地貌的响应

作为岩石圈拉张的产物，裂谷盆地接受了大量陆源碎屑沉积物。随着裂谷拉张，深水环境逐渐占据主导，浊流在输送沉积物的过程中也变得十分重要。深水裂谷盆地内浊流沉积物的分布受到多种盆外因素的控制，如裂谷盆地的地形、气候变化、物源区变化、海平面升降、相关水系变化等；但直接影响裂谷内沉积物分布的仍为盆内控制因素，其中众多正断层及其排列样式直接控制着半地堑地形的形成（Leeder and Gaw thorpe，1987；Ravnås and Steel，1998；Gaw thorpe and Leeder，2000）。因此，正断层的生长发育直接控制了与裂谷盆地相关的地貌变化，进而控制着盆内浊流沉积物的时空展布特征。

从构造的角度看，正断层具有典型的上盘下降、下盘上升的运动学特征，断距在断面中心处达到最大值，沿走向朝断层末端逐渐减小至零。断层走向上的断距变化使得断层下降盘沿走向有向斜构造，相对应地，断层上升盘具有背斜构造，同时断层两端常发育断层传播褶皱（Schlische，1995；Gawthorpe and Leeder，2000；Geetal.，2017）。流体力学数值模拟研究揭示了非限定、自然尺度的浊流垂直流向三维正断层的水动力响应过程和沉积物分布特征。浊流流经正断层地貌主要在以下3个区域发生沉积物的堆积：（1）正断层上升盘小型背斜处浊流反射回流所形成的横向沉积区；（2）正断层下降盘坡脚处水跃作用及下降盘前缘浊流反射回流所形成的横向沉积区；（3）正断层下降盘反向斜坡顶部沉积物与浊流二次反向底流改造作用相关的横向沉积区（图14；Geetal.，2017）。

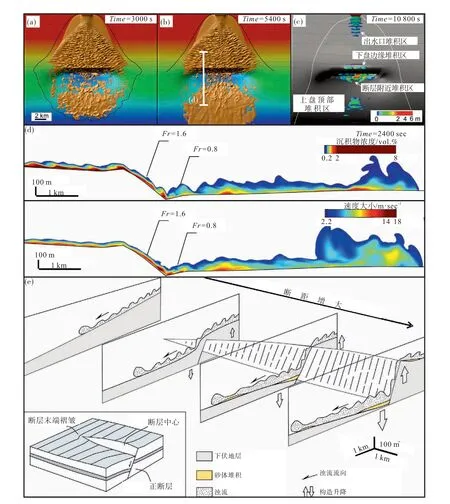
图14 非限定性浊流对正断层地貌响应的流体动力学数值模拟结果与原理示意图（据Ge et al.，2017；有修改）Fig.14 Computational Fluid Dynamics numerical simulation results and schematic diagram of response of unconfined turbidity current to normal fault topography（modified from Ge et al.，2017）

裂谷盆地初期至成熟期，多个呈雁列式分布的小型正断层往往在区域拉张应力作用下通过断层末端的断层传播褶皱不断相互连接、生长，最终形成大型贯穿式断层。生长过程中同倾向的断层之间多发育转换斜坡地貌（Cartwrightetal.，1995；Cowie，1998；Gawthorpe and Leeder，2000；Gupta and Scholz，2000；Walshetal.，2002；Nicoletal.，2005；Athmer and Luthi，2011；Fossen and Rotevatn，2016）。断层转换斜坡一方面能够在相邻断层之间传递构造应变，另一方面会成为相邻断层之间、从上升盘隆起处到下降盘沉积中心处重要的沉积物运输通道（Gawthorpe and Hurst，1993；Morley，1995；Imberetal.，2004；Athmer and Luthi，2011；Fossen and Rotevatn，2016）。

随着断层段生长连接过程中断距、重叠距离和分隔距离的持续变化，浊流对于转换斜坡也会形成具有差异的响应特征：对于早期转换斜坡，其垂向断距和重叠距离仍较小，浊流仅在转换斜坡处沉积过路，未发生明显的沉积；对于成熟期转换斜坡，其具有更大的垂向断距和重叠距离，当断层间分隔距离较小，则浊流对转换斜坡的响应与单个断层类似，但当断层间分隔距离较大，浊流逐渐倾向于在转换斜坡处发生转向并在断层下盘向斜处发生沉积物的堆积（图15；Geetal.，2018）。

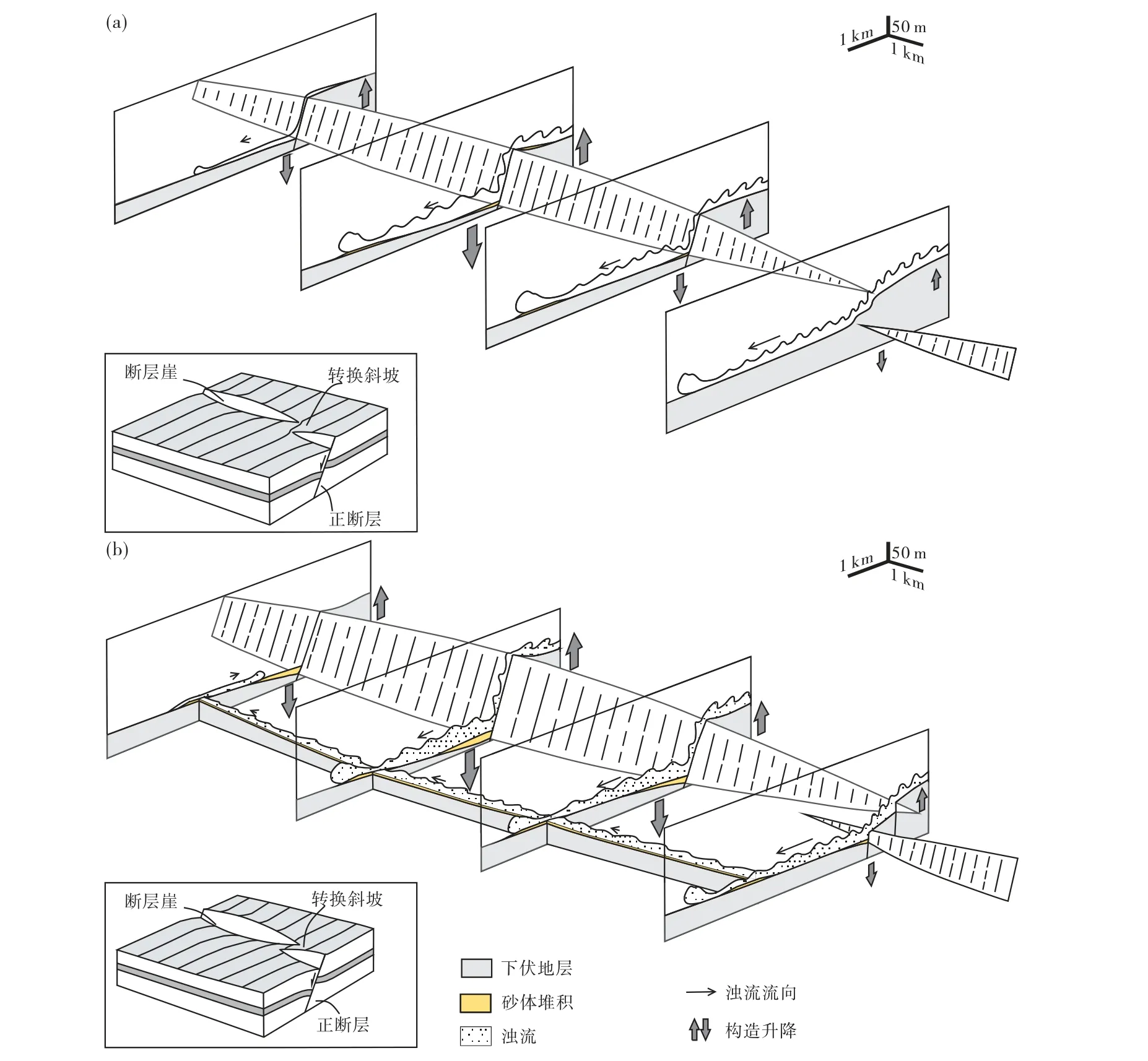
图15 非限定性浊流对转换斜坡地貌响应的模型示意图（据Ge et al.，2018；有修改）Fig.15 Schematic diagram of response of unconfined turbidity current to relay-ramp topography（modified from Ge et al.，2018）

与褶皱地貌类似，浊流流向与正断层（转换斜坡）走向之间的夹角同样决定了浊流的流态及正断层（转换斜坡）附近沉积物的分布模式。现有的研究大多采用野外露头（Cullenetal.，2020）、物理模拟与数值模拟相结合的方法（Athmeretal.，2010）等。野外露头的不足之处在于无法从盆地尺度定量分析入射角的控制作用；而物理模拟与数值模拟相结合的方法存在模型尺寸与自然尺度之间的放缩问题，无法做到真实的自然尺度模拟。因此，入射角的变化对于浊流在正断层（转换斜坡）附近的控制作用亟需高精度的流体动力学数值模拟甚至是浊流原位观测的结果来定量分析。另一方面，浊流对于正断层（转换斜坡）的复杂结构样式的差异响应研究仍可进一步细化，如定量分析正断层的断距、断面倾角、断层上下盘的坡度等，以及转换斜坡的破碎方式（下盘、上盘、双重和中心破碎）（Fossen and Rotevatn，2016；Plenderleithetal.，2022）等对于浊流沉积模式的控制作用。

3.3 浊流对微盆地地貌的响应

含盐（泥）盆地在重力滑脱与重力扩展作用下，使得下伏的塑性盐（泥）岩发生变形，盐（泥）岩由盐撤凹陷驱替至邻近的盐（泥）底辟，使得后期形成的沉积中心位于盐撤凹陷之上的小型“碟状”向斜即为微盆地（Hudecetal.，2009；Jackson and Hudec，2017）。微盆地是陆坡之上典型的海底构造地貌，其广泛分布于含盐（泥）等下伏塑性基底的被动大陆边缘盆地，如墨西哥湾盆地（Mayalletal.，2010；Wuetal.，2020）、西非下刚果盆地（Doughty-Jonesetal.，2017，2019）、巴西桑托斯盆地（Gamboa and Alves，2015；Rodriguezetal.，2018，2021）。而且其集中发育区域往往处于这些盆地的深水区，因而也往往发育了浊流沉积系统。微盆地内浊流的充填是沉积物供给与构造活动形成的可容空间共同控制下的结果。Prather等（1998）将墨西哥湾大陆坡上的微盆地划分成了3类可容空间：阻塞盆地可容空间（ponded-basin accommodation）、斜坡可容空间（slope accommodation）、愈合—斜坡可容空间（healed-slope accommodation）。在此基础之上，对微盆中浊流沉积模式进一步发展，形成了经典的微盆地充填模式——“充填—溢出”模式，其强调了微盆地内沉积物的充填是沉积物驱动、同时由微盆沉降来调节可容空间的一个动态过程。充填—溢出模式将微盆地的充填细化为4个阶段：（1）浊流阻塞阶段：流向微盆地的浊流被微盆地的强限制作用完全捕获，发生沉积物的堆积；（2）浊流剥离阶段：随着微盆地底部沉积物的堆积，其地形起伏相对减小，浊流中相对细粒的组分由上部低密度浊流所携带并越过地形的起伏阻挡，输送至下游的微盆地中；而相对粗粒的组分则在下部高密度浊流的自身重力作用下，在盆地边缘的反向斜坡处反射回流并快速堆积沉积物；（3）浊流过路阶段：浊流以下切、侵蚀的方式发生沉积过路，主体流入顺坡方向下游的微盆地之中，或在局部地形偏转或沉积物供给方向变化下，浊流流动路径改变使得先存微盆地可容空间废弃；（4）细粒沉积披覆阶段：微盆地及周围地形因基准面的上升而被细粒沉积物（深海披覆泥）所覆盖（图16；Badalinietal.，2000；Beaubouef and Friedmann，2000；Boothetal.，2000，2003；Sinclair and Tomasso，2002；Beaubouefetal.，2003；Beaubouef and Abreu，2006）。

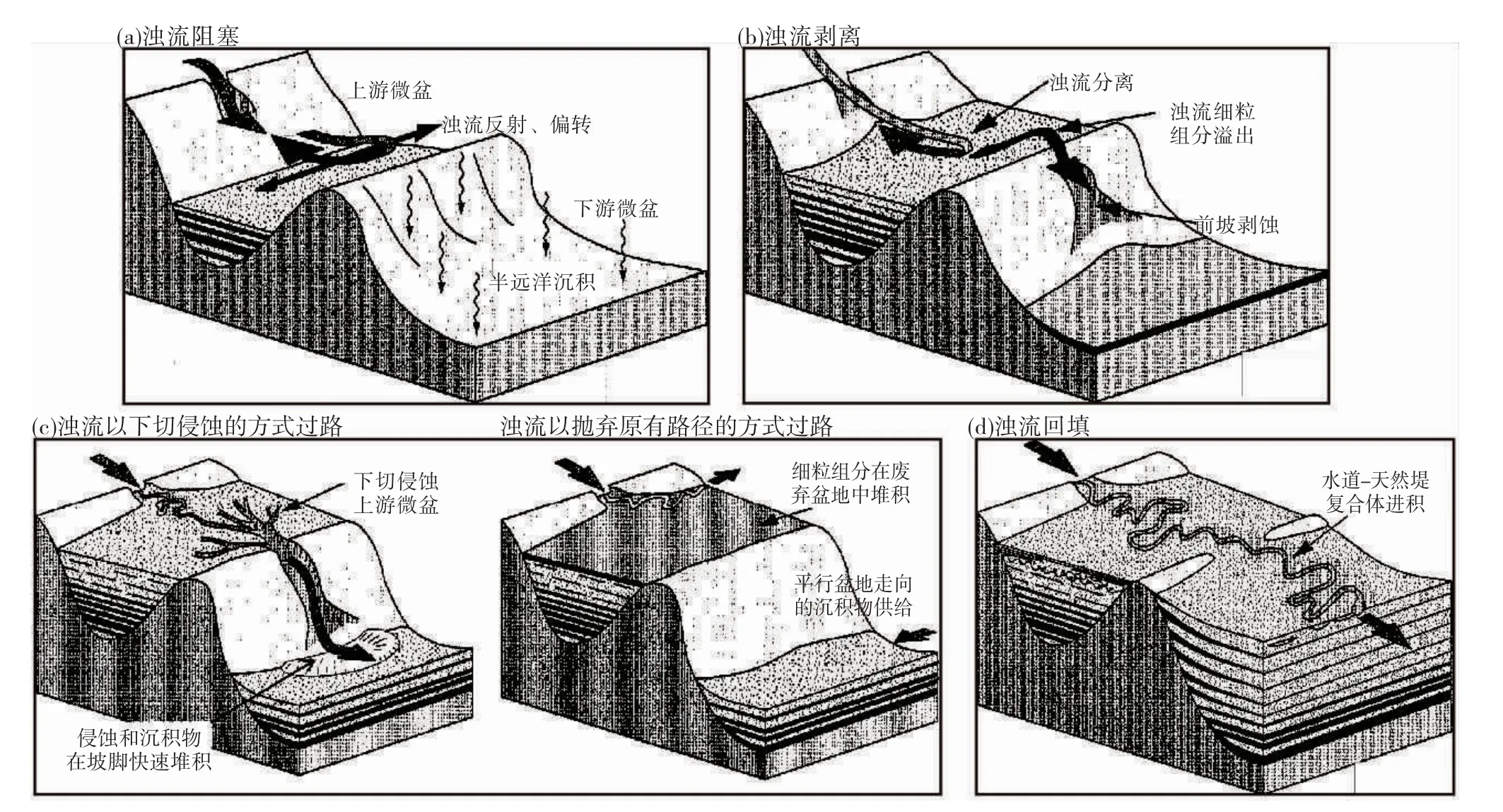
图16 限定性浊积盆地递进式充填及下游盆地坡底伴生沉积模式（据Sinclair and Tomasso，2002；有修改）Fig.16 Depositionalmodel for the progressive infill of a confined turbidite basin and associated deposits at the base of the slope of a lower basin（modified from Sinclair and Tomasso，2002）

经典微盆地 “充填—溢出”模式的不足之处在于其仅考虑了微盆地充填过程中的盆地沉降调节作用，而未考虑到这一过程中盐底辟活动性对于微盆地可容空间的动态控制。随着浊流携带的沉积物不断为微盆地所捕获，微盆地内部沉积物堆积速率存在一定差异性，沉积中心处沉积物堆积速率往往大于周边区域。同时，区域构造活动会导致盐岩变形，如挤压作用可驱替盐岩至两侧盐底辟导致微盆地深度加大，而在拉张作用下底辟顶部发生凹陷形成新的微盆地等。上述沉积物速率、构造活动结合区域水深变化共同控制了微盆地的沉降机制（Hudecetal.，2009）。考虑到微盆地与盐底辟的共同演化，在墨西哥湾微盆地内与浊流相关块体搬运复合体（MTCs）的沉积过程模型基础上发展出了“中心沉降—边缘滑塌”模式，其可划分为3个阶段：（1）浊流初始滞留阶段；（2）中心沉降—边缘隆升阶段：随着微盆地沉积中心处远源沉积物的堆积，在差异负载作用下，微盆地中心不断沉降，两翼盐底辟不断生长；（3）边缘滑塌阶段：随着两翼盐底辟的不断生长，微盆地边缘的盐底辟上覆地层发生滑塌断裂，产生近源的块体搬运复合体并被微盆地所捕获，促进微盆地的进一步沉降。上述3个阶段的不断循环使得微盆地内部充填了多期次的块体搬运复合体、泥质浊流沉积和半远洋沉积（图17，图18；Madofetal.，2009，2017；Wuetal.，2020）。虽然 “中心沉降—边缘滑塌”模式主要针对块体搬运复合体和泥质浊流（Doughty-Jonesetal.，2017，2019；Wuetal.，2020），但是其对于浊流在微盆地的沉积仍具借鉴意义。尤其是在浊流充填微盆过程中，微盆周围底辟活动及相关滑塌作用所形成近源浊流使浊流的沉积模式更为复杂。

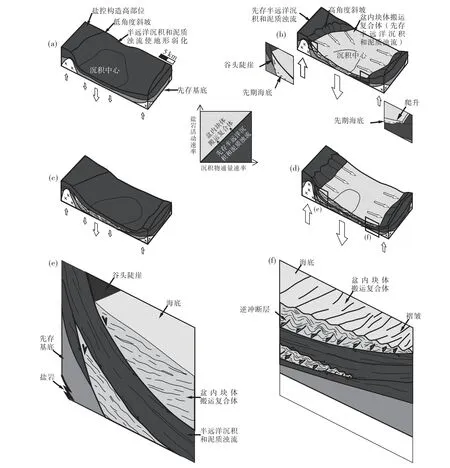
图17 盐构造控制下微盆地内块体搬运复合体循环形成的概念模型（沉降与隆升箭头的相对大小示意了构造活动的相对速率；据Madof et al.，2009）Fig.17 Conceptualmodel showing salt-controlled cyclic generation of intrabasinalmass transport complexes（MTCs）（the relative sizes of subsidence and uplift arrows indicate the relative rates of tectonic activity；after Madof et al.，2009）

图18 “充填—溢出”模式（a）与 “中心沉降—边缘滑塌”模式（b）的比较（据Madof et al.，2017；有修改）Fig.18 Comparison of fill-and-spillmodel（a）and subsidence and margin failure model（b）（modified from Madof et al.，2017）

微盆地内部浊流的水动力响应，早在本世纪初期就通过大量的水槽实验揭示了浊流整体呈现为近端水跃、远端反射回流的 “充填—溢出”模式（Lambetal.，2004，2006；Violetetal.，2005；Tonioloetal.，2006a，2006b；Maharaj，2012），但微盆地内部浊流多次反射回流可能形成的内部环流对于沉积物分布的控制作用仍不明确，仍需高精度的流体动力学数值模拟来定量研究自然尺度下浊流对微盆地的响应。此外，针对微盆地的充填模式，无论是偏向于微盆沉积特征的浊流事件水槽实验（Violetetal.，2005；Khan and Im ran，2008；Sequeirosetal.，2009；Spinewineetal.，2009；Maharaj，2012），还是偏向于微盆构造演化的砂箱物理模 拟（Callotetal.，2016；Mianaekere and Adam，2020），都无法同时考虑微盆地内浊流沉积与盐构造活动的相互作用。近年来取得长足发展的数值模拟方法，只揭示了静态微盆地内地层充填过程中沉积中心向上游方向退积叠置的现象（Wangetal.，2017；Bastianonetal.，2021）；Sylvester等（2015）为数不多地考虑了动态充填过程，但也仅是建立微盆地沉积过程中简易的沉积物质量平衡模型，聚焦于沉积物供给与盆地沉降之间的相互作用，但未考虑下伏盐岩活动所控制的微盆地可容空间的变化。因此，未来可综合利用基于地球动力学的构造数值模拟和基于盆地沉积动力学的沉积数值模拟，将二者联动起来，并通过改变相关构造参数（盐岩流动性、微盆地深度、平面长宽比、剖面纵横比等）和沉积参数（沉积物通量、水通量、降水量、沉积物输送系数等）在盆地尺度上定量分析构造—沉积耦合下微盆地内浊流的动态充填过程。

3.4 浊流对坡折地貌的响应

顺坡而下的浊流所流经的海底坡度往往发生一定变化，局部坡度迅速减缓处即为坡折（slope break；Mutti and Normark，1987）。在自然界中，坡折的分布非常广泛。例如，从大陆坡向深水盆地的过渡中，往往会出现坡折带。当浊流流经坡折处时，坡度减缓，产生以水道—朵叶转换带及伴生的周期阶坎为典型的自生地貌。因此，浊流在缓坡处发生水跃，逐渐由过路转变为沉积，并在坡折下游形成沉积物堆积区（Garcia and Parker，1989；郭彦英和黄河清，2013；Cartignyetal.，2014；Pohl，2019；杨宇平，2020；侯明才等，2022；Hodgsonetal.，2022；钟广法，2023）。

水槽实验揭示了浊流对坡折响应的机制：坡度的减小直接减少了重力作用于浊流下坡方向的分量，当该分量小于浊流所遇到的阻力时，浊流将在流速剖面上呈现出边界区减速和增厚。因此，浊流剪切力减小、携沙能力降低，最终形成沉积物的堆积。浊流流经坡折时，密度分层程度减弱，使得悬浮沉积物在垂向上混合程度更高，表明坡折所引起的湍流增强（Grayetal.，2005）。

在浊流携沙能力驱动与密度分层增强的复合作用下，坡折下游的沉积物堆积具有一定的粒径粗化现象；同时，坡折下游泥沙淤积和堵塞作用逐渐形成一个反向斜坡（坡折下坡坡度减小甚至为负值），超临界浊流减速增厚转变为亚临界浊流的过程中发生水跃，使得坡折所导致的沉积物堆积位于坡折下游方向的一定距离内（图19；Garcia and Parker，1989；Pohl，2019；Pohletal.，2022）。坡折控砂受到上坡坡度和下坡坡度的同时控制：砂体上倾尖灭点的位置受上坡坡度的控制，而沉积物堆积厚度的增加受下坡坡度的控制。上坡坡度的增加使得上倾尖灭点向下坡方向迁移，斜坡砂体与坡折底部砂体之间的连通性减弱；下坡坡度的增加使得沉积物堆积厚度逐渐减小，但不影响上倾尖灭点的位置（图19；Pohl，2019；Pohletal.，2020）。

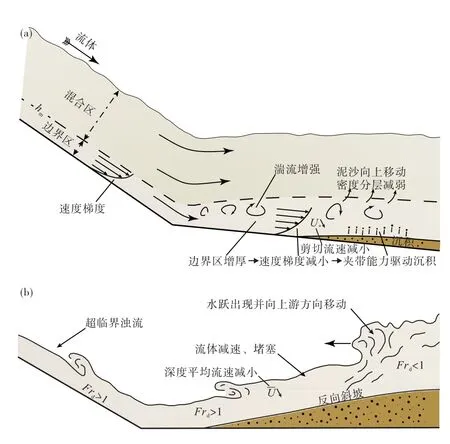
图19 浊流流经坡折（a）并在坡折下坡堆积沉积物形成反向斜坡（b）的流体与沉积动力学概念模型（据Pohl，2019；Pohl et al.，2020；有修改）Fig.19 Flow-dynamic model for a turbidity current crossing a slope break（a）and depositing on the lower slope，later the deposited sediment forms an adverse slope（b）（modified from Pohl，2019；Pohl et al.，2020）

在坡折及其下游方向水跃的诱发作用下，该区域多形成水道—朵叶转换带并伴生一系列以周期阶坎为典型特征的超临界流底形（Mutti and Normark，1987；Masellietal.，2021）。周期阶坎是由超临界流和亚临界流频繁交替产生水跃作用所引起的一系列向流体上游方向迁移的自生地层沉积序列（Zhongetal.，2015；操应长等，2017b；Slootman and Cartigny，2020；王大伟等，2020；钟广法，2023）。周期阶坎的坡度变化使得流经的浊流由超临界态向亚临界态转化，产生水跃。在此过程中，背流面的超临界浊流持续加速，使得底床的剪切应力增加，泥沙夹带速度逐渐大于泥沙沉降速度，从而在背流面发生侵蚀作用；当浊流抵达迎流面的反向斜坡时，浊流流速逐渐降低，转变成亚临界流，使得底床的剪切应力减小，泥沙夹带速度逐渐小于泥沙沉降速度，从而在迎流面发生沉积作用（图20；Cartignyetal.，2014；Zhongetal.，2015；王大伟 等，2018，2020；Slootmana and Cartigny，2020）。根据周期阶坎背流面与迎流面的沉积速率与侵蚀速率的相对大小，可将周期阶坎划分为：完全沉积型、部分沉积型、过渡型、部分侵蚀型与完全侵蚀型（Slootman and Cartigny，2020；钟广法，2023）。

图20 周期阶坎形成的示意图和水槽实验快照（据Postma et al.，2009，2014；Slootmana and Cartigny，2020）Fig.20 Definition diagram and snapshot during flume experiment of cyclic steps（after Postma et al.，2009，2014；Slootmana and Cartigny，2020）

值得说明的是，浊流对于周期阶坎的响应研究是迄今为止唯一得到浊流原位观测证明的。Hughes Clarke于2013年6月对加拿大斯阔米什河河口前缘的前三角洲进行了长达6天的原位观测，期间直接记录到多次涌浪式浊流流经平面呈新月形的周期阶坎时，流体厚度在迎流面突然增厚发生水跃的现象，且观测期间的多次多波束测深证实了浊流流经周期阶坎的前后其背流面侵蚀、迎流面沉积、整体向上游方向迁移的现象（Hughes Clarke，2016）。

4 结论与展望

浊流对复杂构造地貌的响应特征是在对浊流不断深入研究中发现的科学问题。尽管大量的模拟实验研究和多种水动力分析方法使在复杂地貌区预测浊流沉积成为可能，但由于获取浊流流态和沉积物浓度等参数过于困难，同时实际地貌又过于复杂。因此，从浊流在各类地貌下的微观水动力响应机制到构造盆地内的宏观沉积分布仍然存在着较大的鸿沟。因此，浊流对各类构造地貌的宏观响应模式仍然是目前相关研究的重点。总的来说，浊流对多种复杂构造地貌的响应集相似性与差异性为一体。在褶皱后缘等地貌的相对高点处，浊流重力势能增加，浊流反射回流在上游方向堆积沉积物，反向流的强度控制沉积物堆积范围；在褶皱前缘等地貌的相对低点处浊流重力势能减小，浊流水跃并在下游方向堆积沉积物，水跃强度控制沉积物堆积范围。同时，由于不同地貌的样式差异，浊流在不同地貌中的沉积特征又有不同：

1）由逆冲断层／盐（泥）底辟构造引起的褶皱地貌中，浊流整体在褶皱后缘发散偏转，在前缘汇聚偏转，部分浊流反射回母流，部分浊流从褶皱顶部溢出至下游，形成褶皱后缘和前缘2处沉积物堆积区。

2）由正断层及其组合引起的正断层地貌中，浊流整体在断层上盘水跃，部分浊流由于断层上、下盘的三维构造差异发生局部反向流动，形成断层下盘边缘、上盘坡脚及斜坡顶部3处沉积物堆积区。

3）由下伏塑性地层（盐岩／泥岩）的活动所形成的微盆地地貌，浊流整体呈现为近端水跃、远端反射回流的 “充填—溢出”模式。

4）由坡折引起、以水道—朵叶转换带及伴生的周期阶坎为典型的自生地貌中，浊流在缓坡处发生水跃并形成沉积物堆积区。

尽管在浊流对复杂地貌的响应上取得了相当的进展，但当前的研究结果仍以基于野外露头、三维地震、水槽实验的定性—半定量研究为主，缺乏定量的浊流原位观测和数值模拟研究。因此，未来研究重点可朝着定量化、真实化、构造—沉积耦合等方向发展：

1）在当前基于原位观测明确浊流流体结构的基础之上，对全球范围内、典型构造地貌进行定量化原位观测研究。

2）在原位观测获得更多浊流流体参数基础之上，通过流体动力学数值模拟揭示浊流对于多个组合型复杂真实构造地貌的响应，在机理上更好地了解浊流的水动力过程，为深水油气勘探建立真实可靠的自然尺度地质模型。

3）由于盆地演化的复杂性，可以考虑构造与沉积之间的相互控制作用，例如可以采用构造砂箱模拟与水槽物理模拟相结合、地球动力学构造数值模拟与盆地沉积动力学数值模拟相结合等综合方法，定量揭示构造—沉积耦合作用下浊流对构造地貌的响应机制。