核心素养视角下广东中考数学试题的比较研究

郭金秋

【关键词】数学核心素养；比较研究；中考

一、问题提出

当前教育工作中关注的重中之重是如何培养学生的数学核心素养，而课程改革、教学实践、教育评价是落实学生核心素养发展的三个重要渠道．破解中国学生发展核心素养评价难题，更好地培养学生的数学核心素养，亟须研制核心素养为本的评价技术．毋庸置疑，中考是初中阶段最具权、最具说服力的教育评价，同时是检验学生学习效果、教学质量的主要手段，因此中考数学试题是初中数学核心素养的优秀测评案例，然而广东省中考数学试题核心素养测评的实证研究几乎没有．为此，笔者基于喻平教授的核心素养评价框架，对2020年3套广东中考试卷进行比较研究，并在测评的基础上探究出中考命题建议和教学策略．

二、试卷概述

2020年广东省共有三份中考数学试题，分别是2020年广东省初中学业水平考试（简称广东省卷）、2020年广州市初中毕业生学业考试（简称广州市卷）、深圳市2020年初中毕业生学业考试（简称深圳市卷）．广东省卷共25题，满分120分；广州市卷共25题，满分150分；深圳市卷共23题，满分100分．广东省共21个地级市，除广州市和深圳市自主命题外，其余市皆考查广东省卷．与往年不同的是2020年广东省教育考试院不再颁布广东省初中学业水平考试大纲，坚持以课程标准为命题依据．

三、测量体系与测量框架

（一）测量体系

数学核心素养的评价是数学学习评价的一种，因此数学核心素养的评价属于数学学习评价的范畴，成熟的学习评价模型有以下几个：（1）布鲁姆模型，（2） PISA测试，（3）SOLO分类理论，（4）《普通高中数学课程标准（2017年版2020年修订）》对核心素养划分为“毕业水平”和“高考水平”．喻平教授吸取布卢姆模型、PISA模型的长处后提出了数学核心素养的评价框架，该评价框架具有比较充分的理论基础和可操作性，朱先东与吴增生利用喻平的数学核心素养评价框架对2017年浙江省10份中考试题进行分析；何萍与章才岔对温州市2017年中考数学试题进行分析．本文采用喻平的数学核心素养评价框架，对广东省2020年3份中考试题进行数据对比分析，并提出以核心素养为导向的中考命题建议和教学策略．

（二）测量框架的确定

喻平的核心素养评价框架将六大数学核心素养划分为“知识理解”“知识迁移”“知识创新”三个水平，如表1．

根据文献[3]中六大核心素养水平的标定，具体试题赋予相应指标的值，接下来笔者介绍一道典型例题的赋值过程，其余题目标定规则相同不再一一列举，

【评注】设BE=x，学生想象和挖掘出折叠变化前后的结构和数量关系，用含x的代数式表示出AE，AB．EB'的长度，演绎推理出AEB'=60°，最终结合三角函数知识构造等量关系．本题既考查直观想象水平2．又考查逻辑推理水平2．该题共3分，考虑到侧重用数学符号表示图形变化前后的特征和數量关系，因此赋值为12-2，R2-1.

四、测量结果

（一）不同素养不同水平的权重汇总

笔者通过对广东省2020年3份中考试卷中每张试题的每道小题的素养赋值，将对应的素养水平相加，得到不同素养的不同水平权重（保留小数点两位），如表2．

数学运算（C）、逻辑推理（R）、直观想象（I）三个素养的考查权重最高，平均值分别为27.67%，23.89%，20.83%．这说明广东省3套中考试卷从数学运算、逻辑推理、直观想象素养出发，考查数学基本数学思想，数学建模和数学抽象考查权重占比较低且相近，分别是9.11%，8.34%．数学抽象和数学建模关系密切，数学建模蕴含数学抽象的过程，所以二者考查权重相近，但二者所占比例较低．这表明广东省中考试题在考查学生理解和创新利用数学模型解决实际情境问题的能力上表现力不足．

（二）各套试卷核心素养的相似程度分析

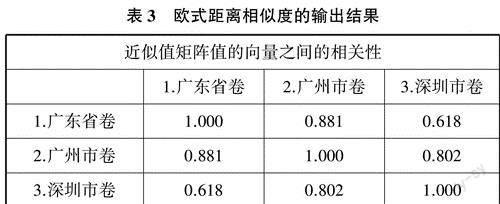
为了进一步探究不同试卷类型中数学核心素养水平考查的相似程度，笔者采用SPSS26.0对表2数据进行相似度测度分析，欧式距离相似度的输出结果如表3．

总体上，不同试卷对数学核心素养的考核大部分相同．由上表可知，各市的试卷在核心素养考核的相似度在60%以上，广东省卷和广州市卷相似度高达88.1%，广东省卷和深圳市卷相似度为61.8%，广州市卷和深圳市卷相似度为80.2%．

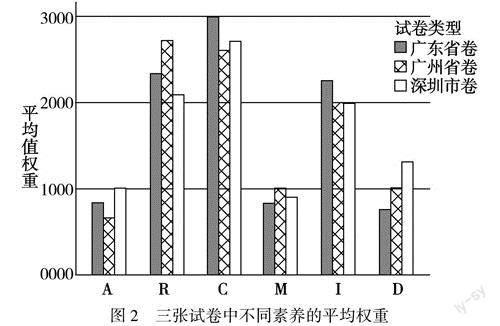
由图2可知，与其他试卷相比，广东省卷更注重数学运算和直观想象能力的考查，对数学建模和数学分析能力的考查所占比重较低．广州市卷对逻辑推理和数学建模的考查比重高于其他试卷的考查，数学抽象能力的考查较低，深圳市卷对数学抽象和数据分析的考查比重高于其他试卷，逻辑推理能力的考查较低．

（三）试卷中核心素养不同水平的分析

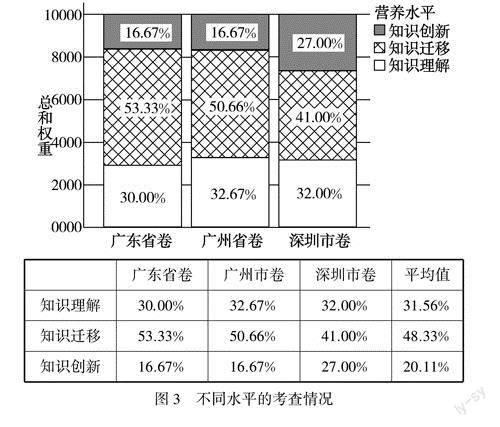
为进一步探究3套试卷对核心素养知识理解、知识迁移、知识创新三种水平的考查情况，采用SPSS26.0软件画得图3．

根据图3三套试卷核心素养的权重总计数据可知，广东省卷、广州市卷、深圳市卷对知识迁移水平的考查分别为53.33%，50.66%，41.00%．这表明知识迁移水平下的核心素养考查是中考试卷命题的主要方向．除此之外，深圳市卷对知识迁移和知识创新水平的考查与其他试卷有较大区别，深圳市卷知识迁移水平的考查比例低于其他试卷，知识创新水平的考查比例明显高于其他试卷，占比为27.00%．同时由表2可知，深圳市卷对数学抽象A3、逻辑推理R3、数学运算C3、数学建模M3、直观想象13的考查都高于广东省卷和广州市卷．

五、命题建议和教学策略

（一）命题建议

第一，认真研读课程标准是中考命题的基础，中考数学命题需符合中国人才培养目标和方向．2020年广东省教育考试院不再颁布广东省初中学业水平考试大纲，坚持以课程标准为中考命题依据，其在评价建议中指出：“在设计试题时，应该关注并且体现本标准的设计思路中提出的几个核心词：数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想，以及应用意识和创新意识，因此加强核心知识与数学核心素养的考查是中考命题的主导方向．

第二，中考命题要处理好知识水平、知识迁移、知识创新三者之间的关系，命题前要通过讨论、研究等方式明确核心素养不同水平的层次划分，以防出现不同试卷对核心素养的水平考查出现分歧的情况.2020年深圳市卷知识迁移水平的考查低于其他试卷，知识创新水平的考查明显高于其他试卷，高出十个百分点．

第三，中考试题设计要注重真实情境化，设置更多以现实生活为背景的题目，进一步提高数学抽象和数学建模素养的考查，将数学思想方法和现实生活相结合，体现“数学源于生活，也服务于生活”．数学核心素养评价注重基础知识，但更关注学生养成运用数学知识阐释、解决实际生活问题的能力．

（二）教学策略

1．注重数学运算素养的培养

麦克斯韦认为：数可以说成是统治整个量的世界，而算术的四则可以被认为是作为数学家的完全装备．首先，解决数学问题离不开数学运算，特别是试卷中难度系数较高的题目都需要大量且复杂的数学运算，其次，每套试卷中都有计算题单独考查学生的数学运算能力，如广东省卷11题、18题、广州市卷12题、13题、17题、深圳市卷17题、18题等，所以3套试卷中考查权重最高的素养是数学运算，教师应保证学生在课堂上的数学运算时间，不能仅仅是引导学生理顺解题思路后将数学运算过程留给课后完成，这将弱化学生对理解算理、选择运算方法，简化运算过程，总结运算技巧的能力，课堂上的限时训练和典型例题示范都不失为提高学生准确、高效、灵活运算的好方法．

2．增强对逻辑推理和直观想象素养的培养

中考对学生思维的灵活性有较高的要求，主要体现在逻辑推理和直觀想象素养的考查上，2020年广东3套中考试卷的压轴题都考查了逻辑推理和直观想象素养的知识创新水平．因此，教师要注重培养学生逻辑思维的系统性，帮助学生把握数学概念的本质并构建知识点之间的关联，包括异同性、所属关系、递进关系等，

具体可以通过变式教学和一题多解培养学生逻辑思维的系统性．变式教学可从变化条件、探求讨论、等价变化、逆向探索、推广等进行多角度、多方位探索，变更事物的非本质属性的表现形式，突出事物的本质属性和隐蔽的本质要素，帮助学生掌握事物本质属性．此外，一题多解帮助学生提高思维的灵活性、变通性和创造性，如深圳市卷中一题多解的题型有15题、22题、23题．

3．创设真实情境，立足能力培养

随着时代的发展，数学与社会经济、科学发展、生态环境等联系日益紧密，对学生关注现实生活，发现生活问题，利用课堂上的知识灵活解决现实生活问题的能力要求越来越高．增强对现实世界现象的理解，获得适应终身发展和社会发展需要的品格和能力是培养学生数学核心素养的功能性目的．学生解决问题往往是从身边的现实问题和自身经验开始，教师应该创造真实的教学情境，基于学生的经验，启发学生思考，引导学生用数学的眼光观察世界，用数学的思维分析世界、用数学的语言表达世界．

例如，在学习函数最值问题时，教师利用“市面上易拉罐的形状大体相近，高度一般是底面直径的2倍，这是巧合还是某种原因呢？”的问题作为引入，通过学生讨论和教师引导提出“当容积一定时，如何设计使得所用材料最省呢？”，将其抽象为函数最值模型进而求解；在学习“锐角三角函数”时，可利用“一架梯子若要架在墙上，有时感觉陡一些，有时感觉平缓一些”为真实情境引入，和学生一起探讨出“陡”和“平”需要用三角函数来刻画，