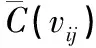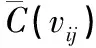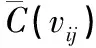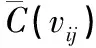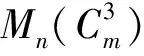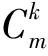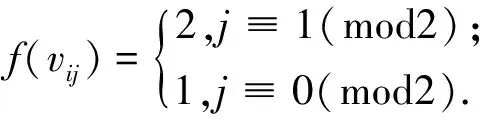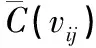广义Mycielski图的邻和可区别全染色

白 羽,强会英

(兰州交通大学 数理学院,甘肃 兰州 730070)

0 引言

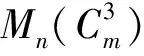
1 预备知识

定义1[2]对简单图G,存在映射f:V(G)∪E(G)→{1,2,…,k},若同时满足:

1) ∀uv∈E(G),f(u)≠f(v);

2) ∀uv,vw∈E(G)且u≠w,f(uv)≠f(vw);

3) ∀uv∈E(G),f(u)≠f(uv),f(v)≠f(uv);

定义2[3]设G是m阶简单图,V(G)={v01,v02,…,v0m},m,n∈N+,图G的Mycielski图Mn(G)是指

1)V(Mn(G))={v01,v02,…,v0m;v11,v12,…,v1m;…;vn1,vn2,…,vnm};

2)E(Mn(G))=E(G)∪{vijv(i+1)k|v0jv0k∈E(G),1≤i≤n,1≤j≤m}.

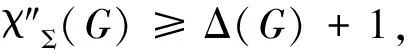
2 主要结论

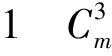
情形1 当m≡0(mod5)时,(0≤i≤n,1≤j≤m),令f为

f(v01v0m)=7,f(v01v0,m-2)=4,f(v02v0,m-1)=5,f(v03v0m)=1.

其余边染法如下:

当i≡0(mod2)时,

f(vi1vi+1,m)=f(vimvi+1,1)=9,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=5,

f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=1,f(vi3vi+1,m)=f(vimvi+1,3)=2.

当i≡1(mod2)时,

f(vi1vi+1,m)=f(vimvi+1,1)=7,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=4,

f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=5,f(vi3vi+1,m)=f(vimvi+1,3)=1.

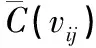
表1 当m≡0(mod5)时,S(vij)和的情况

情形2 当m≠0(mod5)时,(0≤i≤n,1≤j≤m),令f为

其中p

情形2.1m≡1(mod5)时,

f(v01v0,m-2)=5,f(v02v0,m-1)=f(v03v0m)=1,f(v01v0m)=9.

其余边染法如下.

当i≡0(mod2)时,

f(vi1vi+1,m)=f(vimvi+1,1)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=10,

f(vi3vi+1,m)=f(vimvi+1,3)=2,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=7,f(vi1vi+1,2)=f(vi2vi+1,1)=8.

当i≡1(mod2)时,

f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=1,

f(vi1vi+1,m)=f(vimvi+1,1)=9,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=5.

表2 当m≡1(mod5)时,S(vij)和的情况

情形2.2m≡2(mod5)时,令f为

f(v01v0,m-2)=8,f(v02v0,m-1)=9,f(v03v0m)=2,

f(v0,m-2v0,m-1)=1,f(v0,m-1v0m)=3,f(v01v0m)=4.

其余边染法如下.

当i≡0(mod2)时,

f(vi1vi+1,2)=f(vi2vi+1,1)=5,f(vi2vi+1,3)=f(vi3vi+1,2)=1,

f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=f(vi2vi+1,m-1)=

f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=10,f(vi1vi+1,m)=f(vimvi+1,1)=9,

f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=2,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=8.

当i≡1(mod2)时,

f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=9,f(vi3vi+1,m)=f(vimvi+1,3)=2,

f(vi1vi+1,m)=f(vimvi+1,1)=4,f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=8,

f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=1,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=3.

表3 当m≡2(mod5)时,S(vij)和的情况

情形2.3m≡3(mod5)时,令f为

f(v01v0,m-2)=f(v02v0,m-1)=f(v03v0m)=9,f(v0,m-2v0,m-1)=2,f(v0,m-1v0m)=4,f(v01v0m)=5.

其余边染法如下.

当i≡0(mod2)时,

f(vi1vi+1,2)=f(vi2vi+1,1)=8,f(vi2vi+1,3)=f(vi3vi+1,2)=1,

f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=10,

f(vi1vi+1,m)=f(vimvi+1,1)=7,f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=3,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=6.

当i≡1(mod2)时,

f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=9,

f(vi1vi+1,m)=f(vimvi+1,1)=5,f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=2,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=4.

表4 当m≡3(mod5)时,S(vij)和的情况

情形2.4m≡4(mod5)时,令f为

f(v01v0,m-2)=f(v02v0,m-1)=f(v03v0m)=6,f(v01v02)=5,

f(v0,m-2v0,m-1)=f(v01v0m)=4,f(v0,m-,3v0,m-2)=f(v0,m-1v0m)=3.

其余边染法如下.

当i≡0(mod2)时,

f(vi1vi+1,m)=f(vimvi+1,1)=f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=10,

f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=8,f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=5,

f(vi,m-3vi+1,m-2)=f(vi,m-2vi+1,m-3)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=9,

f(vi2vi+1,3)=f(vi3vi+1,2)=1,f(vi1vi+1,2)=f(vi2vi+1,1)=f(vi3vi+1,m)=f(vimvi+1,3)=7.

当i≡1(mod2)时,

f(vi,m-3vi+1,m-2)=f(vi,m-2vi+1,m-3)=f(vi,m-1vi+1,m)=f(vimvi+1,m-1)=3,

f(vi1vi+1,2)=f(vi2vi+1,1)=5,f(vi1vi+1,m)=f(vimvi+1,1)=f(vi,m-2vi+1,m-1)=f(vi,m-1vi+1,m-2)=4,

f(vi1vi+1,m-2)=f(vi,m-2vi+1,1)=f(vi2vi+1,m-1)=f(vi,m-1vi+1,2)=f(vi3vi+1,m)=f(vimvi+1,3)=6.

表5 当m≡4(mod5)时,S(vij)和的情况

情形1 当k≡1(mod2)时,(0≤i≤n,1≤j≤2k).

f(v0jv0,j+k)=3,f(v01v0,2k)=7,

当i≡0(mod2)时,

f(vi1vi+1,2k)=f(vi,2kvi+1,1)=8,

f(vijvi+1,j+k)=f(vi,j+kvi+1,j)=4,

当i≡1(mod2)时,

f(vi1vi+1,2k)=f(vi,2kvi+1,1)=7,

f(vijvi+1,j+k)=f(vi,j+kvi+1,j)=3,

情形2 当k≡0(mod2)时,(0≤i≤n,1≤j≤2k).

令f为f(vik)=1,f(vi,k-1)=f(vi,2k)=3.

当i≡0(mod2)时,

f(vi1vi+1,2k)=f(vi,2kvi+1,1)=8,

f(vijvi+1,j+k)=f(vi,j+kvi+1,j)=4,

当i≡1(mod2)时,

f(vi1vi+1,2k)=f(vi,2kvi+1,1)=7,

表6 当k≡0(mod2)时,S(vij)和的情况