一维驻波场增强的里德堡原子微波测量
2023-10-08李可田建飞张好景明勇张临杰
李可,田建飞,张好,景明勇,张临杰
(1 山西大学 量子光学与光量子器件国家重点实验室 激光光谱研究所,太原 030006)
(2 山西大学 极端光学协同创新中心,太原 030006)
0 引言
在光与原子分子相互作用研究领域,相干和干涉一直是重要的研究焦点。电磁诱导透明(Electromagnetically Induced Transparency, EIT)是光与物质相互作用中表现出的一种典型的(线性)量子光学效应[1-2],EIT 效应诱导的介质折射率色散增强[3-4]在量子信息存储[5]、微波探测[6]及高分辨激光光谱[7-8]等领域具有巨大的应用前景[9-14]。目前人们已经在碱金属原子[3]、锶原子[15]、铅原子[16]以及红宝石[17]等多种介质中实现了EIT 光谱的测量。近年来,利用双光子激发形成里德堡原子的阶梯型三能级系统,在实现光子相位门[18-19]、量子模拟[20-21]、原子磁力计[22-23]等领域有着极高的研究价值,特别是基于里德堡原子EIT 光谱的微波测量[24]正在成为新的研究热点。
利用空间模式匹配且传输方向相反的耦合光可在原子气室中形成驻波,驻波的空间强度分布由两束耦合光的强度和波长决定。此外,由于驻波场强度由两束耦合光相干合成,因此可有效降低耦合光激光器输出功率。在三能级阶梯型EIT 量子干涉效应中,探测光的吸收和色散系数依赖于耦合光的强度[25-26]以及耦合光的传输方向[27],因此研究耦合光一维驻波场EIT 效应具有重要价值。本文在高增透镀膜的原子气室中,利用反射模式匹配光路形成里德堡铯原子三能级体系中耦合光的一维驻波特征分布,并在此基础上进行了一维驻波耦合光场增强的微波电场测量。其次,探究了不同耦合光场增强效应下电磁诱导透明光谱强度与线宽的变化。最后在不同微波功率下,对比分析了不同耦合光场增强微波电场测量的信噪比以及频率响应曲线表现。
1 实验装置
里德堡原子EIT 耦合光一维驻波场相干增强的微波测量实验系统如图1(a),里德堡EIT 光谱微波测量的能级图如图1(b),852 nm 探测光将Cs 原子从6S1/2激发至6P3/2,510 nm 耦合光将Cs 原子从6P3/2激发至48D5/2,微波电场作用在相邻里德堡态48D5/2及49P3/2。探测光由852 nm 半导体激光器提供,耦合光由510 nm 光纤倍频激光器提供,探测光和耦合光在原子气室内部共线反向传播,探测光经双色片DM1 进入光电探测器。利用透镜组(Lens1 及Lens2)形成近平行耦合光光束,束腰位置被调整到原子气室中心。耦合光光束在通过原子气室后,由双色镜DM2 反射并经透镜(Lens3)使得光束腰位置在全反镜,实现反射光束匹配调节,耦合光反射回原子气室后与入射耦合光形成一维驻波场,一维驻波场的平均光束直径约为800 μm。耦合光反射光路中插入四分之一波片保证耦合光偏振态与入射光保持一致。实验中探测光和耦合光均为竖直线偏振光,偏振方向与被测微波电场的极化方向保持一致。由于里德堡原子能级间跃迁几率较低,为尽量减少原子气室对耦合光的散射,实验中采用高增透镀膜的原子汽室,耦合光单次通过透射率达到98%以上,耦合光经过模式匹配和反馈光学系统后返回原子汽室的光强为入射光强的80%。
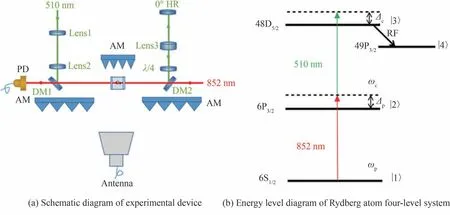
图1 实验装置及能级图Fig.1 Experimental setup and energy level diagram
空间微波电场由微波射频源输出,通过喇叭天线辐射至原子气室中与里德堡原子进行作用,微波频率近共振于48D5/2⇔49P3/2能级谐振频率。为了减少微波天线入射场多径散射的影响,在实验平台周围布置了射频吸波材料,同时尽量保证天线口面与原子汽室之间无电磁反射物。
2 实验测量结果
如图1(b),在实验中探测光频率锁定在6S1/2到6P3/2的共振跃迁线,耦合光的频率在6P3/2到48D5/2的共振跃迁频率附近扫描,构成阶梯型三能级系统。耦合光频率扫描至6P3/2到48D5/2的共振跃迁频率时,探测光透射强度出现吸收减弱的现象形成一个透射峰,即电磁诱导透明现象。实验结果如图2,图中红色三角为耦合光无增强的实验数据,蓝色方块为耦合光一维驻波场增强实验数据,实线为Voigt 函数的拟合结果。虚线为耦合光无增强0 失谐位置。探测光光强为100 μW,可以看到随着耦合光一维驻波场的形成,EIT 光谱幅度提升1.5 倍,线宽提升1.8 倍。同时,由于耦合光一维驻波场功率增强,EIT 光谱中心出现明显的频移。

图2 不同耦合光场增强下的EIT 光谱信号Fig.2 EIT spectrum signal with different enhancement of coupling light
首先,为了研究耦合光功率与EIT 光谱线型的关系,通过增加耦合光激光器功率输出,实验测量了耦合光功率5 mW 到70 mW 的EIT 光谱,如图3(a)中插图所示,图中黑色三角形为实验数据,红色三角数据对应耦合光功率为36 mW,蓝色方块对应数据为耦合光20 mW 情况下形成一维驻波场测得EIT 信号的结果;红色实线为三能级理论拟合结果。利用Voigt 函数对EIT 光谱进行拟合获得EIT 光谱的幅度、线宽及中心频率。图3(a)为EIT 光谱的信号幅度与耦合光功率的关系,当耦合光功率增加至50 mW,EIT 光谱接近饱和;如图3(b),随着耦合光功率的增加,EIT 光谱线宽表现出线性增加,实验结果可定性解释为耦合光AC-Stark效应引起48D5/2里德堡态展宽正比于光功率[28]。图3(a)和3(b)中蓝色方块为入射耦合光功率20 mW,反射光功率为16 mW 情况下形成的一维驻波场测量得到的EIT 光谱信号幅度与线宽。

图3 不同耦合光功率下EIT 光谱信号强度与线宽Fig.3 EIT spectra signal intensity and linewidth at different coupling optical powers
图中可以看到相较于耦合光功率36 mW 时,一维驻波场增强EIT 信号的幅度增加1.2 倍,线宽增加1.4 倍。实验结果表明通过耦合光的空间模式匹配以及偏振对准,入射光与反射光在原子气室内形成了相干叠加,其光强可近似表示为
式中,Ii为入射光强,Ir为反射光光强,φ(z)为两束光的相对相位,z为光传输方向的相位位置。实验中Ir=0.8Ii,由式(1)可得一维驻波场的形成使得原子气室内的等效光强增加约3.6 倍,入射光强度20 mW 情况下原子气室内等效光强约为72 mW。从图3(a)及3(b)中可以看到,耦合光直接输出功率为70 mW 时对应的EIT 信号幅度和线宽仍然低于一维驻波场形成后得到的信号强度,因此需要进一步考虑室温原子热运动的多普勒效应对EIT 光谱信号的影响。
对于阶梯型里德堡原子三能级体系,在弱探测光近似下,原子介质的极化率表示为χ=χ'+iχ″, 实部χ'和虚部χ″分别与原子介质的色散和吸收特性相联系。极化率χ的表达式[29]为
式中,ω21和ω32分别为图1(b)中能级跃迁|1>⇔|2>和|2>⇔|3>的频率,g21为基态到中间态跃迁的矩阵元,衰减率γij=(Γi+Γj)/2,Γi(j)为能级|i>的自发辐射衰减率,Δp为6S1/2⇔6P3/2跃迁的失谐量,Δc为其对应于6P3/2⇔48D5/2跃迁的失谐量。Ωc=2γ32Ec是耦合光的拉比频率,N(ν)为麦克斯韦玻尔兹曼速度分布。
由于气体中原子或分子时刻处于无规则的热运动状态,不同原子的运动速度和方向各不相同,因而多普勒效应所产生的频移也各不相同。由于一维驻波耦合光场增强中,既存在与探测光同向的耦合光,又存在与探测光反向的耦合光,两种情况下考虑原子热运动导致的多普勒效应,对耦合光的的失谐是不同的,通常耦合光与探测光的频率失谐量需要加入多普勒补偿项。对于耦合光与探测光同向传输情况,有
对于耦合光与探测光反向传输情况,有
实验中对探测光频率进行了锁定,扫描耦合光频率获得EIT 信号。由于多普勒效应导致的补偿项正好符号相反,因此当同向传输和反向传输两种情况同时存在时,EIT 信号分别由不同速度群的原子所贡献,表现为一维驻波场增强的EIT 信号幅度更高同时线宽展宽更为显著。
为研究不同耦合光功率下里德堡原子微波电场测量的特性,首先测量微波电场作用下EIT-AT 分裂光谱,如图4。图4(a)对应的耦合光功率为20 mW,图4(b)对应的耦合光功率为36 mW,图4(c)对应的是20 mW 耦合光形成一维驻波场增强情况下的EIT-AT 分裂光谱,图中实线为双峰拟合结果。理论上分裂光谱的双峰拟合对应频率间隔Δf正比于微波电场强度E[24]。

图4 不同耦合光场增强下微波共振位置处EIT-AT 分裂光谱Fig.4 EIT-AT splitting spectrum at microwave resonance position under different coupling optical field enhancement
对于相同的微波输出功率,图4 中测得的分裂间隔如表1。可以看到随着耦合光功率的增加,双峰的分裂间隔有所增加。这是由于较大的耦合光功率将引起里德堡能级移动,从而导致微波频率与相邻里德堡原子能级的失谐δRF[30],因此A-T 分裂光谱间隔表示为
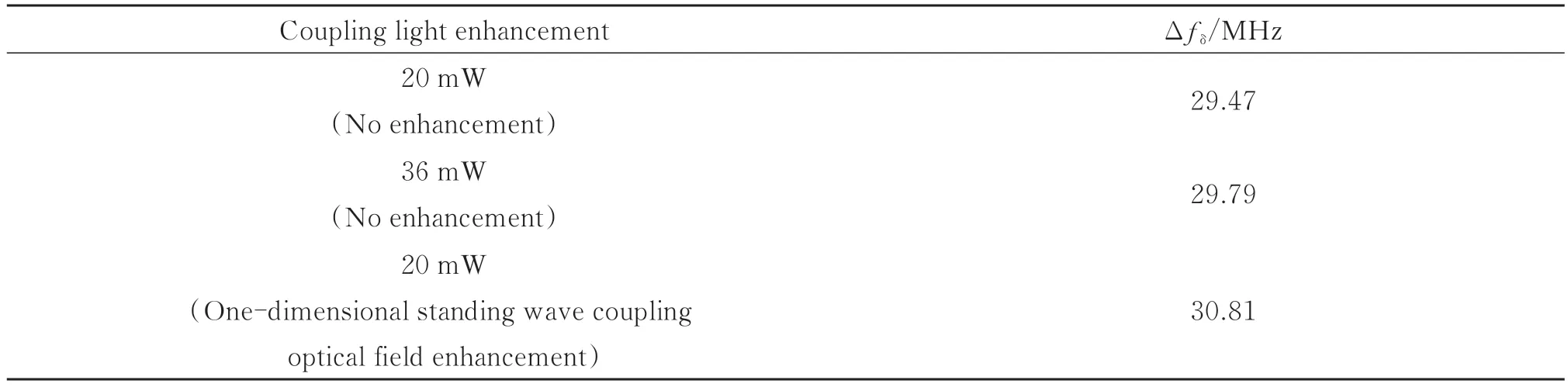
表1 不同耦合光场增强下A-T 分裂间隔Table 1 A-T splitting interval under different coupling light enhancements
式中,Δƒδ是实测A-T 分裂间隔,δRF是微波失谐量,Δƒ0是微波频率共振下A-T 分裂间隔。由式(7)可以计算得到,耦合光功率从20 mW 增加到36 mW,引起了里德堡态的能级移动了0.35 MHz,而一维驻波场增强情况下,里德堡能级移动约1.38 MHz。
为研究不同耦合光场增强在不同微波功率下对微波电场测量的影响,实验中耦合光与探测光频率分别锁定在原子能级共振位置,测量了幅度调制下的微波信号,调制信号的频率为100 kHz。光电探测器的输出信号接入频谱分析仪,在分析频率100 kHz 处记录功率谱信号。在微波源输出功率为-8 dBm 与0 dBm 下,测量不同微波频率下微波电场测量的信噪比如图5 和图6。在图5 与图6 中(a)对应的耦合光功率为20 mW,(b)对应的耦合光功率为36 mW,(c)对应的是20 mW 耦合光形成一维驻波场增强时不同微波频率下微波电场测量的信噪比。微波电场测量的信噪比最大值下降3 dB 对应的微波频率范围由橙色标出。
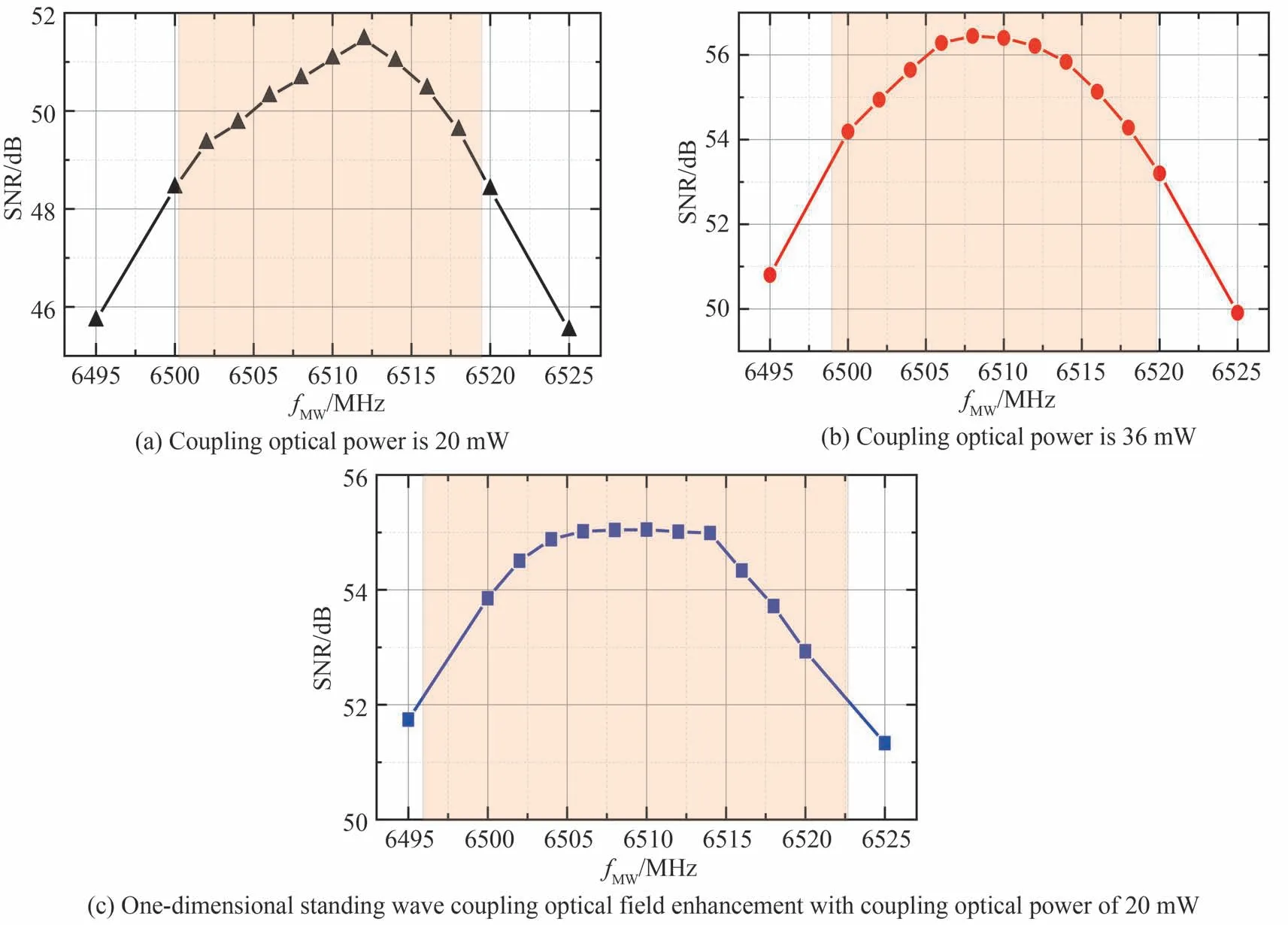
图5 不同耦合光场增强下微波电场测量的信噪比随微波频率的变化关系,微波功率为-8 dBmFig.5 The relationship between signal-to-noise ratio of microwave field and microwave frequency was measured under different coupling optical field enhancements. The microwave power is -8 dBm
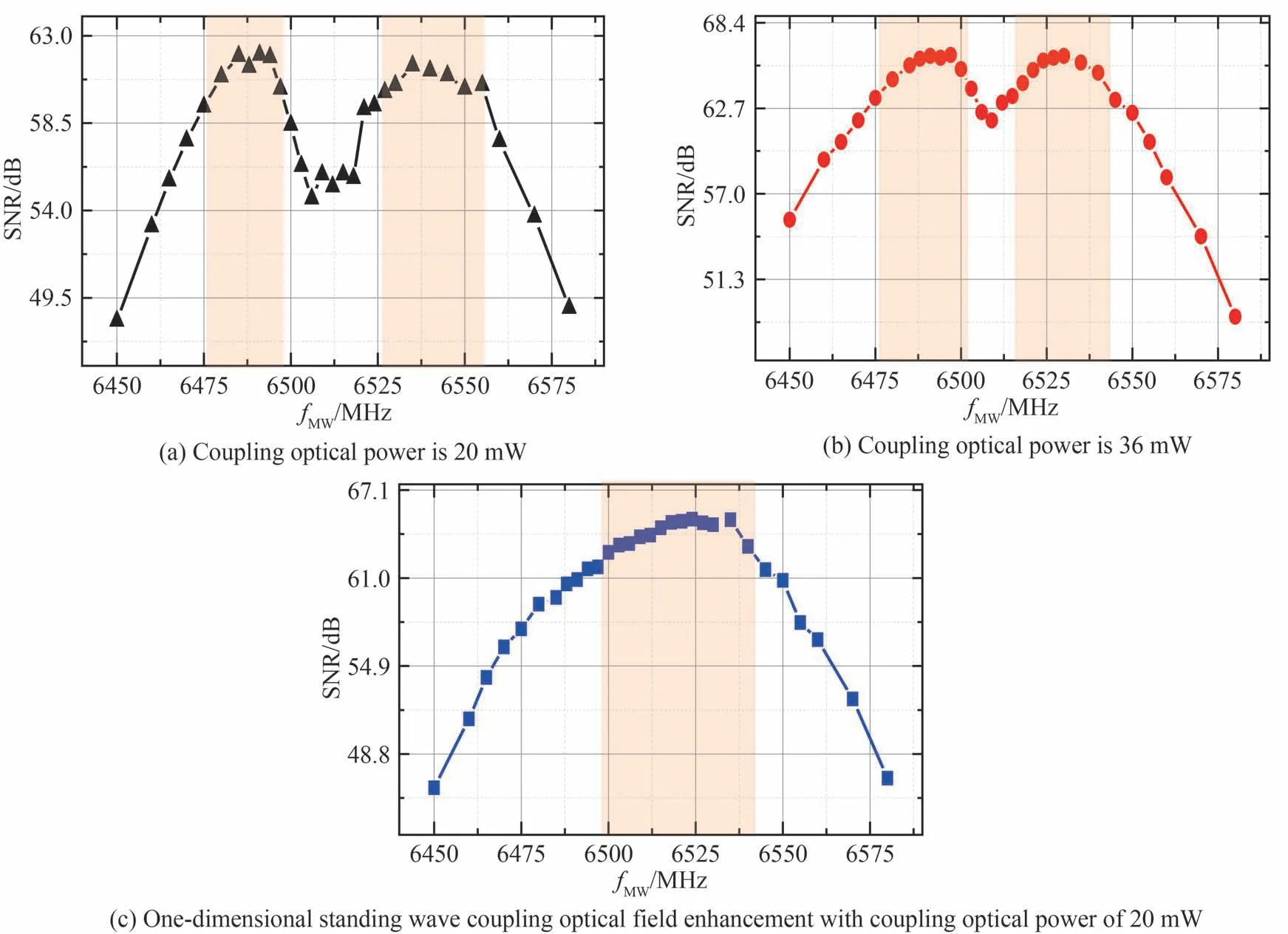
图6 不同耦合光场增强下微波电场测量的信噪比随微波频率的变化关系,微波功率为0 dBmFig.6 The relationship between signal-to-noise ratio of microwave field and microwave frequency was measured under different coupling optical field enhancements, the microwave power is 0 dBm
实验结果表明:在微波功率较低时,耦合光功率为36 mW 对比耦合光功率为20 mW 测量微波频率信噪比提升约5 dB,带宽提升107%;而耦合光功率同样为20 mW 时,一维驻波场的存在使测量微波频率信噪比提升约4 dB,带宽提升138%。在微波功率较高时,无驻波场存在的微波响应曲线呈现出明显的双峰形态,而一维驻波场的形成可有效消除双峰特征,表现为平坦响应特征。
3 结论
本实验通过基态、激发态和里德堡态构成阶梯型三能级系统,在高增透镀膜的原子汽室中,利用反射匹配光路实现里德堡铯原子三能级体系中耦合光的一维驻波特征分布,在室温原子气室中获得了里德堡原子的EIT 光谱信号,研究不同耦合光场增强对EIT 光谱信号的影响,保证入射耦合光光强不变的情况下,在原子汽室中形成一维驻波耦合光场增强可实现电磁诱导透明光谱强度提升150%和线宽提升180%。在此基础上通过射频电场耦合相邻的原子里德堡态,在实验中观察到EIT 信号的分裂。对比分析了不同耦合光场增强微波电场测量的信噪比以及频率响应曲线表现,实现了一维驻波耦合光场增强的微波电场测量。在保证入射耦合光光强不变的情况下,一维驻波耦合光场增强在较低微波功率下可使测量微波频率信噪比提升约4 dB,带宽提升138%,同时在较高微波功率下一维驻波场的形成可有效消除双峰特征,表现为更平坦的响应特征。里德堡原子的量子相干效应提供了一种测量射频电场的新方法,而里德堡原子EIT 一维驻波耦合光场相干增强可为进一步研制低功耗、频率响应曲线平坦,动态范围更大的自校准电场测量传感器提供新思路,对发展相应的计量标准等具有重要的应用价值。
