相位自校准的光纤微波频率绝对相位传递

张晋铂，胡亮，李奇，陈建平，吴龟灵

（上海交通大学 电子信息与电气工程学院 区域光纤通信网与新型光通信系统国家重点实验室， 上海 200240）

0 引言

时间和频率作为基本物理量，是诸多应用领域的研究基础，例如基础物理学验证、基于时钟的大地测量、定位和导航等领域［1-4］。光纤凭借其损耗低、带宽大、抗电磁干扰强等优点，成为了高稳定时频传递理想介质的选择。目前主流频率传递方案可大致分为光学频率、光频梳以及射频传递三种［5-9］。然而，绝大多数现有的时间频率传递系统只能保证在系统运行的过程中相位差恒定，而忽略了当系统重启或改变了系统链路长度时，在重新锁定后有可能会发生的相位差变化。这种情况无法满足某些相干应用的需要，比如分布式相控阵雷达、射电望远镜阵列等。这些应用不仅需要在运行过程中具有稳定的相位差，而且要求多次重启后相位差的值不发生改变［10-13］，可以在不同站点之间提供同频同相的参考信号，实现更有效的相干处理［14-16］。

2020 年SI Hongwei 等提出了一种光纤绝对相位传递方案［17］。该方案基于相位共轭的补偿方法，多次重启的情况下相位波动占一个周期的2%。但是该方案采用多级电路混频，会引入额外的噪声。2021 年，WU Rui 提出了一种基于时间测量的绝对相位传递方案，使用往返的时间差对频率信号进行校准，从而消除相位周期模糊度，使得相位波动占一个完整周期的1%［18］。但是其采用了波分复用的方案进行传递，时间信号与频率信号使用不同的光波长进行传输，这会导致传输信号时延出现差异，使得时间信号测量得到的链路时延不能准确反映出频率信号通过的时延，需要对系统进行复杂的标定。

本文提出一种基于可调光延迟线的光纤微波频率绝对相位传递方案。该方案充分利用时间信号的往返传输延时来确定频率信号相位的整数个周期，结合对微波频率的高精度相位测量，在系统多次关机重启的情况下，能够在远端获得与本地端信号相位差固定的微波频率信号。由于方案采用窄带的声表面波滤波器的输出信号［19-20］作为时间测量信号，可以通过频分复用方式将时间信号与微波频率信号耦合在同一个波长信道中进行传输，从而避免了在不同波长传输引入的时延差等问题。相较于其它时间频率同传方式［21-23］，该方案系统更加简单，无需采用多种调制方式，也不直接对1PPS 信号进行调制，采用窄带滤波器即可将时间信号与微波频率信号分离使其互不影响。实验结果表明，当系统经历多次重启，相位差的波动在0.008 rad 左右，约占一个周期的0.15%，可保证较高的相位一致性。

1 基本原理

1.1 时间信号的获得以及链路时延的测量原理

通过使用声表面波滤波器的输出信号作为时间信号计算得到链路时延，其原理如图1。首先在预处理阶段使用雪崩三极管将1PPS 信号转化为脉冲信号，其电路如图2。

图1 时间信号产生及测量原理Fig. 1 Time signal generation and measurement principle

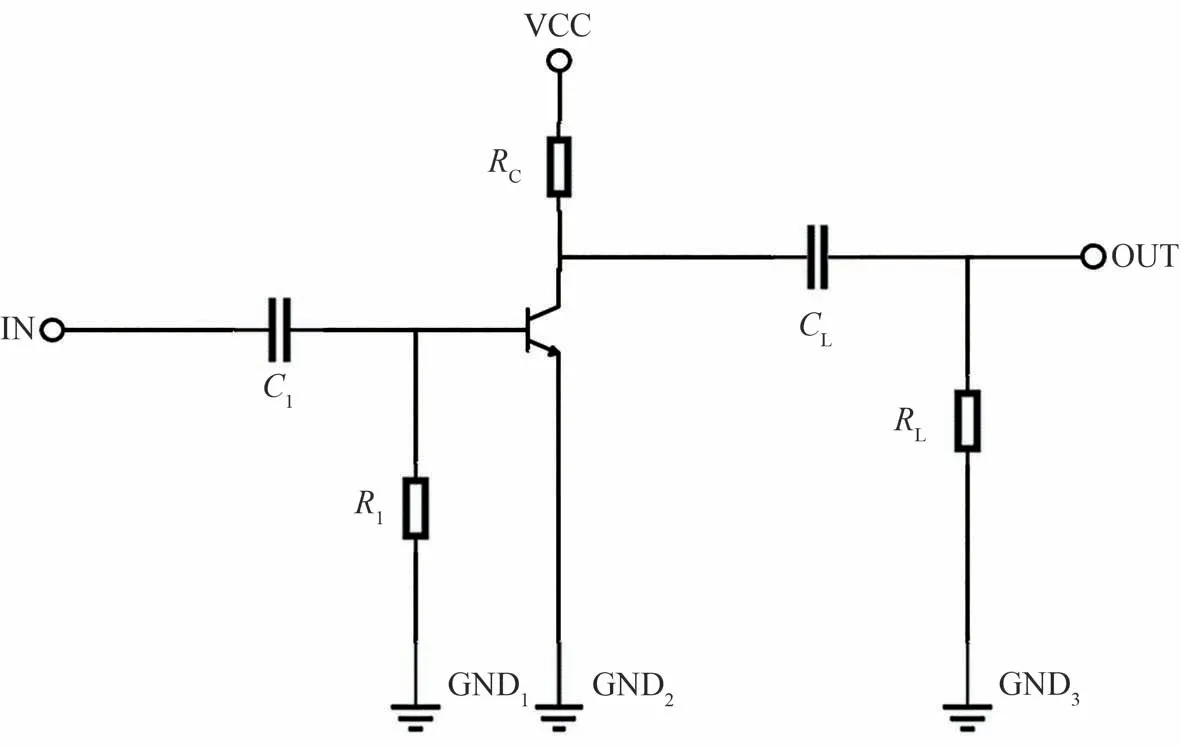
图2 雪崩三极管脉冲产生电路图Fig. 2 Circuit diagram of pulse generation using avalanche triode

在输入端，电容C1与电阻R1构成了一个RC 微分电路。在没有触发脉冲时，雪崩三极管没有正向偏压同时保持截止状态，此时电源VCC 通过集电极电阻RC对电容CL进行充电使CL的电压等于VCC 的电压，达到雪崩临界状态。当输入端输入一个方波信号，经过RC 电路后触发的电流到达基极，使三极管基极电流发生改变，三极管发生雪崩击穿效应产生突然增加的雪崩电流，储能电容CL通过负载电阻RL进行放电。CL储存的电荷有限，在大的雪崩电流的作用下会形成一个峰值较大，宽度较小的窄脉冲信号。由于雪崩三极管内部电感作用，放大电流逐渐提高到峰值形成窄脉冲前端，电容上电荷逐渐放电，电流由峰值逐渐减小形成窄脉冲的后端，这样负载电阻RL则会在每一次触发脉冲作用下形成窄脉冲信号［24］。

得到脉冲信号后使用声表面带通滤波器后的信号作为时间参考信号。声表面波滤波器的主要作用是将输入的脉冲信号转化为窄频带外高度抑制的信号。理想的带通滤波器冲激响应在频域上表现为通带内为常数而通带外为0，忽略幅值可以表示为

式中，B为滤波器的带宽，rect()为矩形窗函数。根据傅里叶变换可得其在时域上为

最终得到的时间信号时域和频域如图3。由图可知经过声表面波滤波器得到了一个时域上类似抽样函数的包络信号，在频域上表现为窄带信号，中心频率为70.5 MHz，3 dB 带宽为4 MHz。

图3 时间信号时域及频域结果Fig.3 Frequency domain results and time domain results of time signal

采用广义互相关法计算时间差，将用于测量时延的两路时间信号分别使用模数转换器（Analog to Digital Converter， ADC）进行采集，采集后的信号发送到现场可编程逻辑门阵列（Field Programmable Gate Array， FPGA）中进行插值重构以提高时间测量的精度。使用重构后的时间信号做互相关可得

两路信号的附加噪声与重构信号不相关，而附加噪声之间只有当τ较小时才部分相关，随着τ的增大，附加噪声的相关函数会减小，当其值趋于0 时̂(τ)取得最大值，此时对应的τ值记为待测时延，即

由于互相关的平均效果，可以消除两路信号中的附加噪声成分，降低系统本底噪声，提高时间测量的精度［20］。

1.2 绝对相位传递原理

相位自校准的光纤频率绝对相位传递的原理如图4。本地端信号源用于输出时间参考信号（Ts）和频率基准信号（Fs）。不考虑其幅度，频率基准信号可以表示为余弦函数，记为

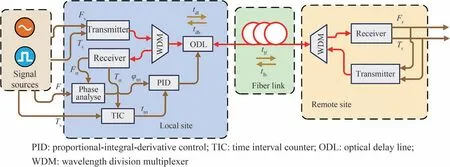
图4 相位自校准的光纤频率绝对相位传递原理Fig.4 Schematic of absolute phase of radio frequency transfer on fiber with phase self-calibration

式中，ω0和φ0为待传递频率信号的角频率和初始相位。使用功分器将时间参考信号与频率基准信号进行合束后调制到光上，输入到波分复用器（Wavelength Division Multiplexer， WDM）和可调光延迟线（Optical Delay Line， ODL）后经光纤传输到远端。在远端经过另一个WDM 与光电探测器后通过带通滤波器恢复出时间信号（Tr）和频率信号（Fr）。Fr可以表示为

式中，tf正向传输引入的总延时，φf为链路正向传输引入总相位，根据相位与时延的关系有φf=ω0tf。tdf和tlf为光延迟线引入延时和链路正向传输引入延时。在远端将恢复的时间和频率信号合束后调制到另一波长上，沿相同光纤链路发送回本地端，在本地端恢复出往返时间信号（Trt）和频率信号（Frt）。携带有链路噪声信息的Frt可以表示为

式中，tb为链路中反向传输引入的总延时，φb是链路中反向传输引入的总相位，φb=ω0tb。tdb和tlb是链路中反向传输引入的延时和反向信号通过光延迟线引入的延时，这里假设往返链路的正向传输时延等于反向传输时延，即tb=tf，φb=φf。因此往返的时延（ttrt）和相位（φtrt）可以表示为

在本地端，通过混频获得Frt和Fs之间的相位差φtrt。利用Trt和Ts得到往返的链路时延ttrt。由于有相位周期模糊的存在，所以得到的φtrt只是在一个周期之内的相位差。使用所得的相位差作为误差信号对光延迟线进行比例-积分-微分（Proportion-Integration-Differentiation， PID）控制，当相位补偿装置工作在稳定状态时，有如下关系

将式（12）代入式（6）可知在远端恢复出了相位稳定的频率信号。

若想重启之后保证远端微波信号相位保持不变，首先需要选取未重启时的往返相位差为基准，记为φre，在系统多次重启之后，期望每一次重启有如下关系成立

此时，φf可表示为

要实现上述功能，首先需要选择未重启时的往返时延作为参考基准，记为tre，当ttrt=tre时，φtrt=φre，此时。当系统多次重启后，若是往返时延和基准时延的差（Δtrt）为偶数个频率信号周期，即满足

式中，T0为频率信号的周期，m为整数，且，此时，意味着在一个相对周期内，无需调整。若是往返时延与基准时延的差是奇数个频率信号的周期，即Δtrt满足

式中，m仍为整数。此时需要控制光延迟线改变链路时延直到Δtrt满足式（15），可以得到

式中，φre是选定的参考基准，与链路无关且不会发生改变。这样就实现了绝对相位传递。

2 实验系统搭建

根据图4 实验原理图搭建实验系统。待传递的频率信号为使用微波源（Rigol Inc， DSG830）产生的1 GHz 的信号，同时将微波源的参考10 MHz 信号作为整个系统的频率参考。声表面波滤波器输出的窄带信号作为时间信号。将频率基准信号和时间参考信号使用功分器耦合之后，由调制到电吸收调制器的分布式反馈（Distributed-feedback， DFB）激光器（波长为λ1=1 551.72 nm，线宽为10 kHz，一天内波长漂移小于2 pm）进行光纤链路传输。光信号通过WDM 以及 ODL 后进入光纤链路传输到远端，在远端通过另一个WDM 后由光电探测器（Photodetector， PD）将时间信号和频率信号解调出来，然后分别使用中心频率为1 GHz、带宽为70 MHz 和中心频率为70 MHz、带宽为10 MHz 的两个带通滤波器进行滤波，分别得到所接收的时间信号和频率信号。同样地，将恢复出的时间信号和频率信号使用功分器耦合后加载到另一个内调制的DFB 激光器（波长为λ2=1 550.12 nm）上进行光纤反向传输。在本地端使用同样的方式将时间信号以及频率信号恢复后，使用ADC 采集回传的时间信号和本地时间基准信号进行计算得到链路往返时延。同时利用回传的频率信号和本地频率基准信号进行混频低通滤波后得到误差信号，根据得到的误差信号驱动单片机控制光延迟线（补偿速度）对链路进行补偿。

3 结果与分析

由图3 可得，时间信号是一个中心频率为70.5 MHz，3 dB 带宽为4 MHz 的窄带信号，其中心频率与频率信号的频率并无倍数关系，所以理论上不会影响频率信号的传递。为了对其进行验证，在10 km 链路上对有无时间信号的情况进行频率传输性能测试，所得结果如图5。有时间信号时，频率稳定度为4.95×10-14@1 s，3.21×10-17@10 000 s，之后使本地端产生时间信号的源停止工作，测得无时间信号时频率稳定度为4.01×10-14@1 s，2.16×10-17@10 000 s。可以看出时间信号并不会影响微波频率信号传递的性能。

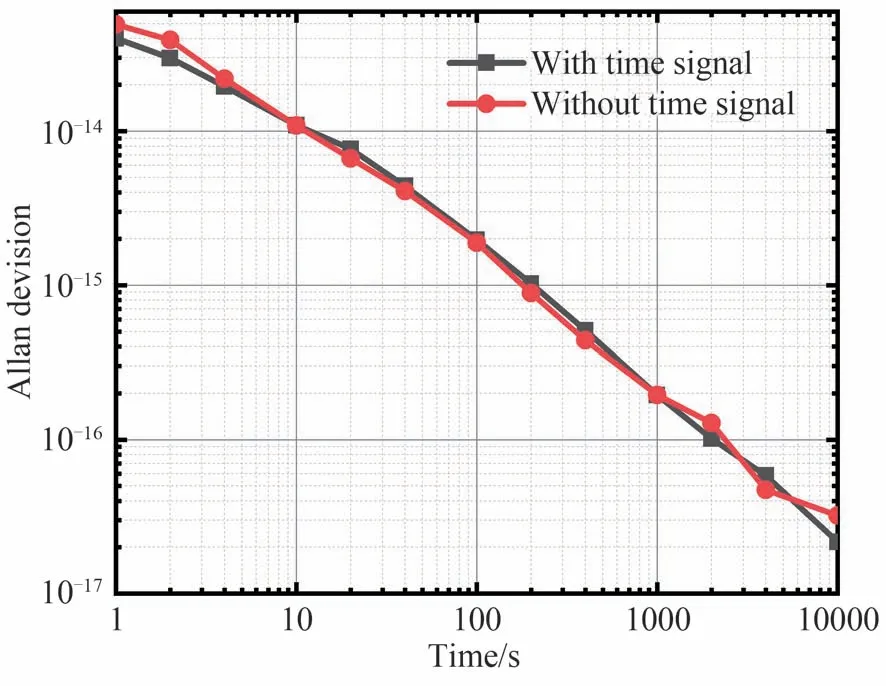
图5 有无时间信号时频率传递性能测试结果Fig.5 Frequency transmission performance test results with or without time signal

实验室环境下，在60 km 光纤链路上进行实验。首先控制ODL 使系统进入稳定状态，根据本地端和远端的数据计算相对频率稳定度，结果如图6。实验采用1 GHz 的微波信号，经过测试相位的均值为0.793 rad，在10 000 s 的时间内测得的相位变化为0.005 rad，系统的频率稳定度优于4×10-14@1 s，5×10-17@10 000 s。与未补偿时的链路相比，万秒稳提升了两个数量级。以上结果证明系统具有较好的补偿效果。

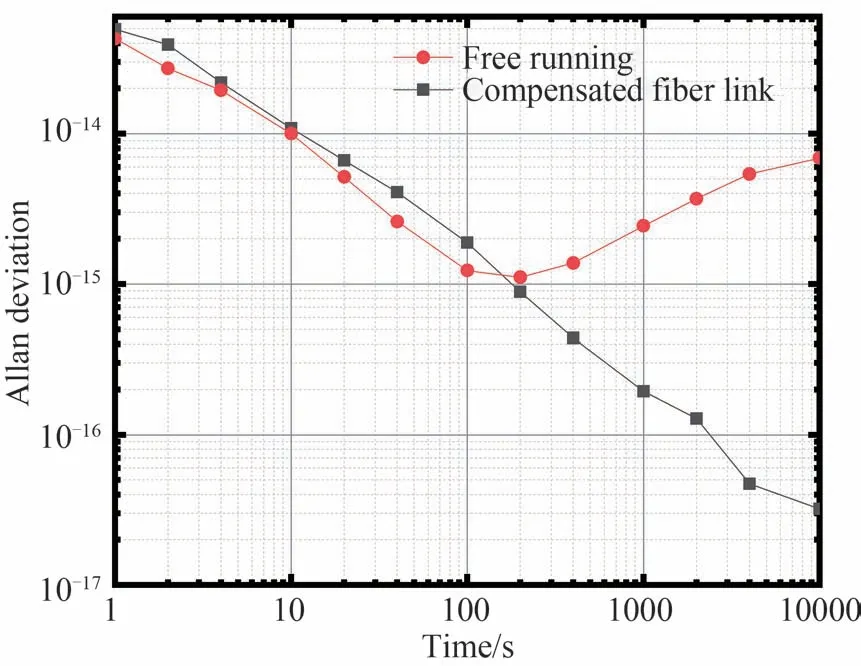
图6 60 km 光纤链路频率稳定度测试结果Fig. 6 Frequency stability test results of 60 km optical fiber links

同时，当系统稳定工作时也可以在远端恢复出稳定的时间信号，图7 给出了稳定前后时间测量的结果。相较链路未稳定时，稳定后的链路测量所得时间稳定度在长稳方面有着明显改善，可达10 ps@1 s，0.3 ps@10 000 s。

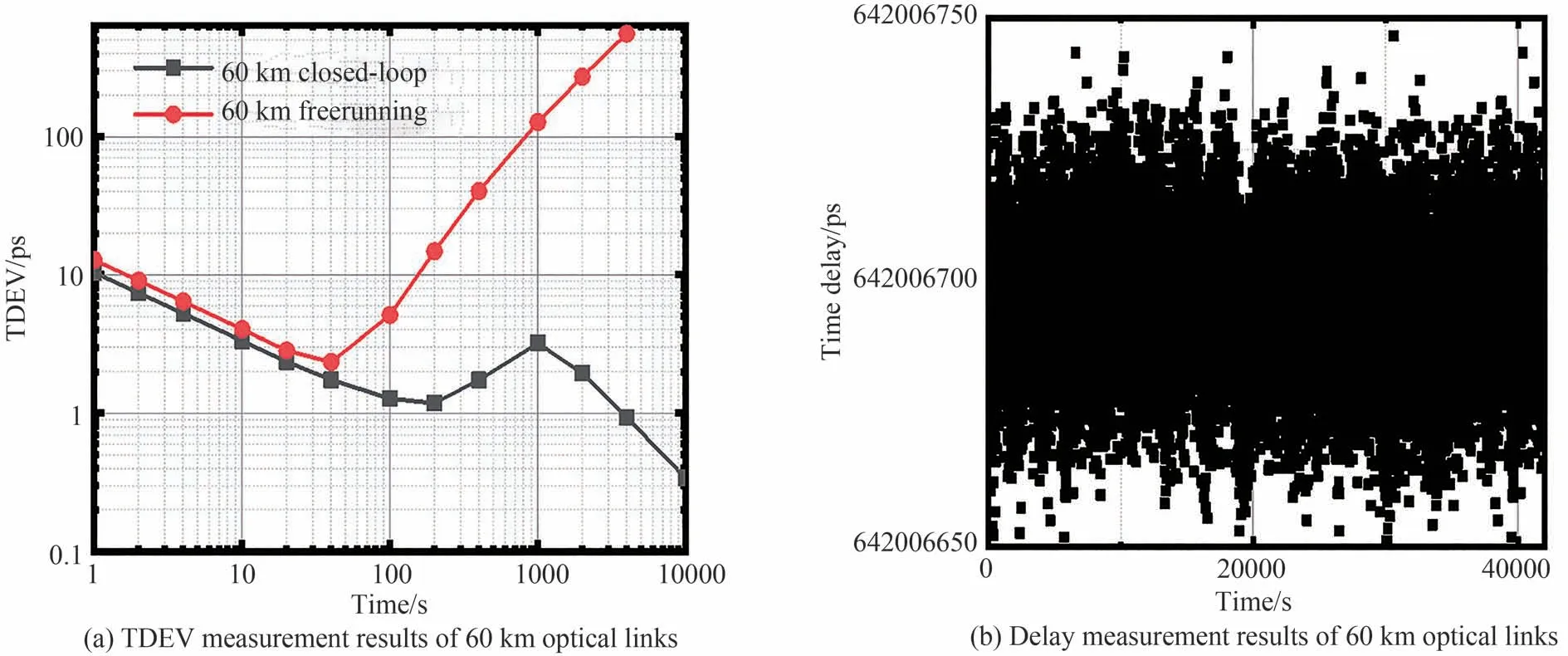
图7 60 km 光纤链路时延测量结果Fig.7 Delay measurement results of 60 km optical links

接着测试了在系统多次关机重启的情况下，光纤绝对相位传递系统能否得到可重复的相位差。首先，采用往返时延来判断是否需要进行校准，并将第一次测量得到的链路时延作为参考基准。由于直接测量的链路时延包含了系统本身的时延，所以要先进行背靠背标定，即使用一段短光纤连接主从两端测量往返时延，在之后的计算中将其扣除以得到链路带来的往返时延。经过多次测量取平均值可获得系统本身时延为671.483 ns。接下来，多次进行重启，每次重启等待链路稳定后重新测量此时的往返时延并与基准进行比较，若是结果相差1 000 ps，则由第一节的原理可知远端与本地端信号相位相差半个周期，此时需要控制光延迟线延迟半个周期即500 ps；若是相差偶数个周期则无需进行操作。经过多次重启后的结果如图8。

图8 60 km 链路时延测试结果以及绝对相位传输结果Fig. 8 Delay test results and absolute phase transmission results of 60 km link

由于本文采用波分复用的方式进行双向传输，前后传输的波长不一致导致双向传输不对称性，需要对波长不一致性进行校准。不对称性带来的双向时延差可表示为

式中，D是色散系数，其值为17 ps/（km·nm），L为光纤长度，Δλ为前后向传输光信号波长差，利用波长计测得前后向传输的光波长差为1.556 nm，从而计算出链路前后向时延差值为1 587.12 ps。

相比于时间的测量，微波频率相位的测量更为精确，所以可以通过频率及式（19）对时间测量进行更精确的标定，可表示为

式中，τ为根据频率计算得到的时延，Δφ为测量得到的相位差，f0为待传输频率信号的频率，本文中信号频率为1 GHz。以时间信号测量所得结果确定整数周期，同时以频率测量结果确定更精确的时间记为τ，结果如表1。

表1 测量得到的往返时延以及标定后结果Table 1 The measured round-trip time delay and the calibration results

如表1 所示，未重启时测得的链路往返时延均值为595 054 101 ps，扣除系统本身时延以及消除波长不对称性所带来的影响后，可以得到单向的链路时延为297 190 515 ps，第一次重启后测得的往返时延均值为595 056 107 ps，与基准相比相差2 006 ps。同时计算得到的单向时延与基准相比相差1 003 s。若时间只考虑整数周期，则第一次重启后往返时延与基准之间相差两个周期，远端得到的信号与基准相差一个周期，这种情况下可认为第一次重启得到的相位差与基准是相同的。同理，第二次重启后所得往返时延为595 055 103 ps，与基准相差一个周期，同时在远端得到的信号与基准相差半个周期，故此时需要控制光延迟线使得延时增大或者减小500 ps。之后再次测量往返时延，直到与基准相差偶数个周期，此时调整完毕。最终调整后结果如图9。图9（a）和（b）展示了第一次和第五次重启调整后的结果，图9（c）展示了经过多次重启之后最终稳定时相位均值的情况。最终多次重启后相位差锁定在0.792 rad 附近，抖动为0.008 rad，而文献［14］中方案以及文献［17］中方案在多次关机重启后相位差抖动分别为0.006 6 rad 以及0.006 rad，与本文结果相差不大，充分说明绝对相位传递系统的良好稳定效果。

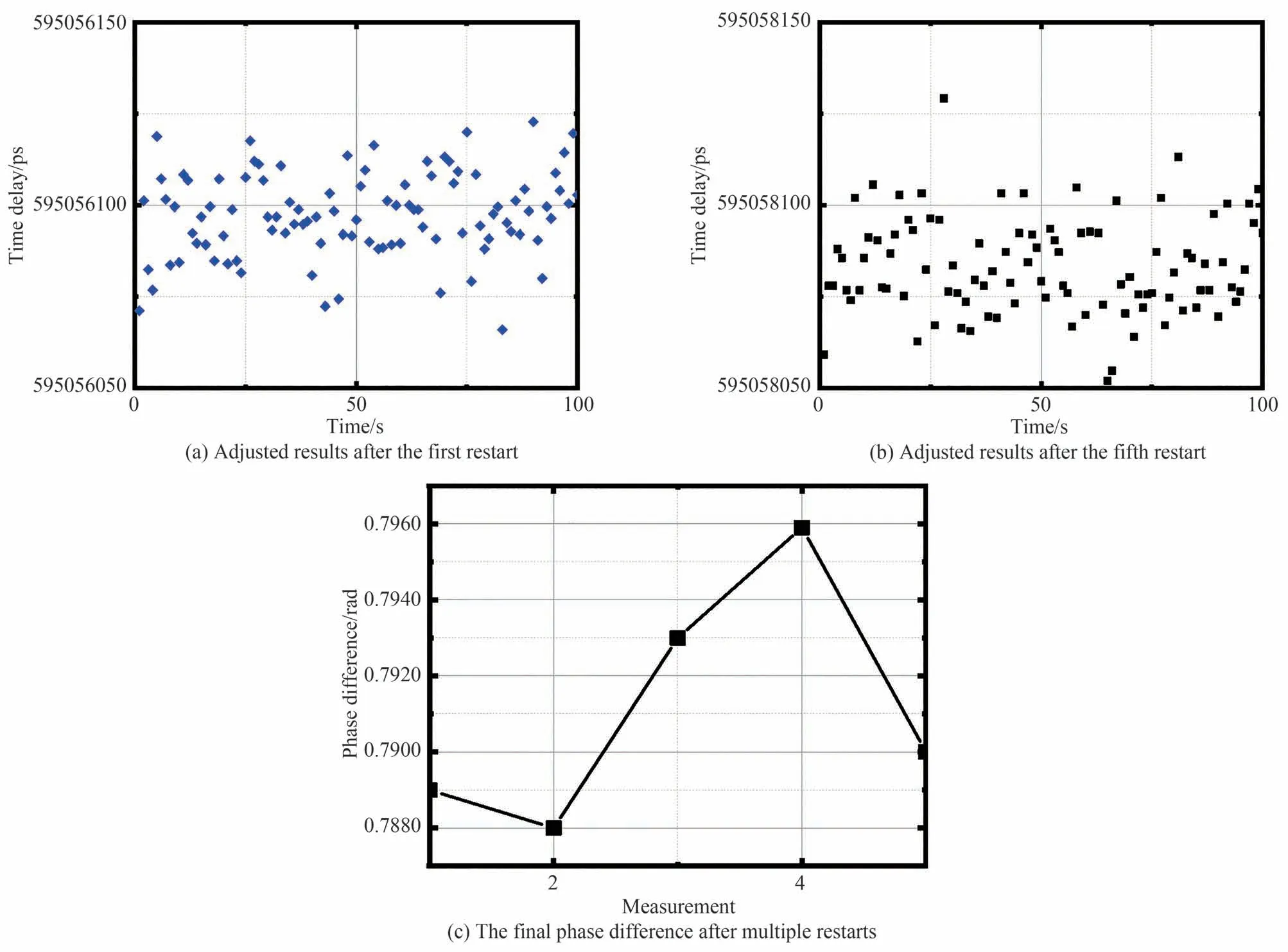
图9 调整后的时延以及最终得到的多次重启后的相位差Fig.9 The adjusted delay and the final phase difference after multiple restarts

4 结论

本文提出了一种光纤绝对相位传递技术，利用往返与本地的频率信号混频滤波后作为误差信号进行补偿，同时将时间信号与频率信号使用同一波长进行传输，避免了因波长不同而导致传输时延不同的问题。此外，利用测量精度较高的微波频率相位来对时间测量结果进行校准，提高了测量精度，实现了光纤链路上本地端与远端可重复的相位差，经60 km 光纤链路传递后系统获得了优于4×10-14@1 s，5×10-17@10 000 s 的频率稳定度。链路稳定后，测得时间传递的稳定度为10 ps@1 s，0.3 ps@10 000 s，表明该方案具有较好的链路补偿效果。当系统多次重启后，远端与本地端的相位差均值的波动在0.008 rad 之内，约占一个周期的0.15%。