非对称振荡并联扑翼能量采集特性数值模拟研究

2023-10-08王宇璐郭凯伦王丽春崔慧娟

机械与电子 2023年9期

王宇璐,郭凯伦,王丽春,崔慧娟

(1.咸阳职业技术学院机电学院,陕西西安 712046;2.西安交通大学能源与动力工程学院,陕西西安 710049)

0 引言

振荡扑翼作为一种可利用流体能的新型清洁能源转换装置,丰富了人们对可再生能源的利用手段。但由于风能、海洋能等流体能具有分散程度高和品质低等问题,导致流体能的能量转换效率很大程度上依赖于扑翼装置的性能好坏,如何优化振荡扑翼装置的能量采集性能成为研发和推广扑翼装置的技术难题[1-2]。扑翼振荡的运动控制参数和振荡模式是决定装置采集效果的关键因素[3-7],而运动控制参数有时受实际应用环境限制,难以有效提升扑翼性能,因此,需要对振荡模式影响扑翼采集效果的规律进行研究。

Ashraf等[8]提出一种扑翼风能与水能采集装置,对比正弦和非正弦振型下的扑翼采集性能;杜晓旭等[9]基于双自由度分析模型研究4种振荡模式下的扑翼水动力特性。以上研究讨论的是向内冲程与向外冲程2个阶段振型对称的振荡模式,尚未针对2个振荡阶段采用不同振型展开研究。

针对上述问题,本文提出一种非对称振荡模式下并联扑翼振荡控制与分析方法。

1 扑翼模型与数值方法

1.1 并联双扑翼计算模型

并联双扑翼结构在流场中的布置形式如图1中虚线框部分所示。扑翼类型选取NACA 0012,弦长c为1 m,初始时刻两扑翼间隔δ为1c。图1以向外冲程为例,展示了并联扑翼在不同振荡时刻的姿态分解。向外冲程时,两扑翼由初始位置分别开始运动,过程中均以沉浮运动耦合俯仰运动的形式振荡,且两扑翼始终保持相反的运动姿态(如图1中纵向箭头所指)。在t/T=0.5时,两扑翼分别到达各自沉浮振荡极限位置,完成向外冲程运动,此时沉浮速度降为0。扑翼由极限位置反向振荡至初始位置的过程即为向内冲程。图1中,参数H和θout分别表示扑翼的沉浮振幅和向外冲程俯仰振幅。

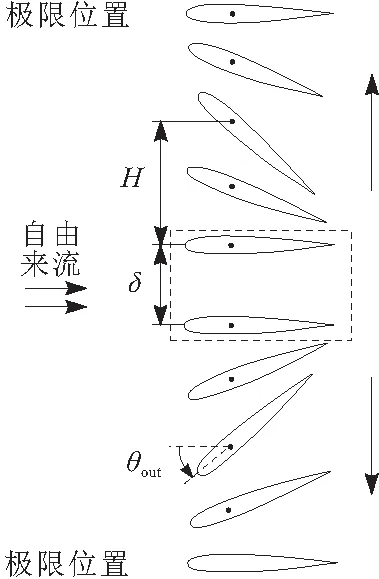
图1 并联扑翼向外冲程运动

针对非对称振荡模式对并联扑翼能量采集过程的影响展开讨论,分析扑翼在不同非对称俯仰振幅振型下的能量采集性能,非对称俯仰运动的控制方程如式(1)所示,α(t)为振荡过程某时刻扑翼的俯仰角;沉浮运动采用对称振型形式,其控制方程如式(2)所示,h(t)为某时刻扑翼沉浮方向位移。

(1)

h(t)=H0csin(2πft+φ+β*)

(2)

θin为向内冲程时的俯仰振幅。当讨论θout对能量采集过程的影响时,保持θin为70°;同理,当讨论θin的影响时,保持θout为70°。f为振荡频率;t为扑翼运动时刻;β*为区分两扑翼控制方程的参数,当描述上侧扑翼时,β*=180°,当描述下侧扑翼时,β*=0;φ为沉浮运动和俯仰运动的相位差,根据Kinsey等[10]的研究,选取φ为90°,俯仰中心轴取距离翼型前端点c/3处。

1.2 数值方法与网格

本文采用空气作为流体介质,由于其不可压缩及粘性特性,空气流动需满足连续性方程和动量方程,其表达式为:

(3)

(4)

ρ为空气密度;u、v、w分别为x、y、z方向的空气流动速度;Fi为i方向上控制体所受体积力;μ为动力粘性系数;Sij为应变率张量形式;g为重力加速度;p为控制体所受压力。

采用层流模型,基于CFD软件和SIMPLE算法对连续性方程和动量方程进行求解,通过二阶迎风格式对空间项进行离散,通过二阶隐式时间步法对瞬态项进行离散。

网格策略直接影响数值模拟的精度和效率。为了以较小计算代价获得满足计算精度要求的模拟结果,对计算域进行内域和外域的分区。图2给出了并联扑翼的计算域和网格划分策略。计算内域为扑翼附近边长为10倍弦长的正方形区域,其外部环绕区域为计算外域。如图2中扑翼表面网格所示,在靠近翼型表面的内域区域划分结构化网格,保障翼型表面流动特性的准确模拟。在内域的其他区域划分较密的非结构化网格,可实现快速更新高质量网格,避免在扑翼振荡过程中发生网格畸变。

图2 并联扑翼计算网格

计算外域距翼型较远,在扑翼振荡过程中出现网格畸变的可能性小,划分较为稀疏的结构化网格,在满足计算精度要求的前提下减少计算量,节省计算资源。内外域交界处网格节点设置一一对应。计算域网格总数为7.6万。采用动网格技术模拟并联扑翼的沉浮俯仰耦合振荡过程,通过C语言程序控制扑翼实现向内冲程与向外冲程不对称的振荡姿态。计算域入口、出口分别设为速度入口、压力出口,上、下边界均设为滑移边界。

1.3 扑翼输出参数

振荡扑翼通过沉浮俯仰耦合运动采集流场能量,所采集到的能量P为

P=Fy(t)Vy(t)+M(t)ω(t)

(5)

Fy(t)为沉浮方向的气动升力;Vy(t)为沉浮振荡速度;M(t)为扑翼所受扭矩;ω(t)为俯仰振荡速度。

为了对不同工况下的扑翼采集性能进行有效对比,故采用无量纲功率系数CP衡量扑翼采集性能的优劣,即

(6)

U∞为自由来流流速;L为翼型展向长度。本文针对二维计算模型,故取L为单位长度。

扑翼整体采集性能通常以1个振荡周期内的功率系数平均值CPm表示,即

CPm=CPhm+CPθm=

(7)

CPhm和CPθm分别为扑翼通过沉浮振荡和俯仰振荡采集的无量纲功率系数;T为振荡周期;Cl和CM分别为升力系数和扭矩系数,分别定义为:

(8)

(9)

扑翼采集来流能量的效率η以所采集到的功率与扑翼扫略范围内的来流总功率之比表示,即

(10)

d为扑翼扫略过的垂直高度,根据Xiao等[11]的研究取d=2H0c。

1.4 网格无关性验证

为了保证所选用的网格划分策略不影响数值计算结果的准确性,对网格进行无关性验证。以f=0.159 Hz,H0=1.0,θ0=80°,δ=1 m工况为例,对网格数为4.9万、7.6万、11.3万时的扑翼计算模型的振荡过程展开讨论。图3给出了3种网格策略下1个振荡周期内振荡扑翼的功率系数CP曲线。由图3可知,不同网格策略下扑翼的功率系数基本一致,网格方案的选取对整体结果的影响很小。因此,为了节省计算资源且同时保证计算精度,研究选取网格数为7.6万的网格策略。

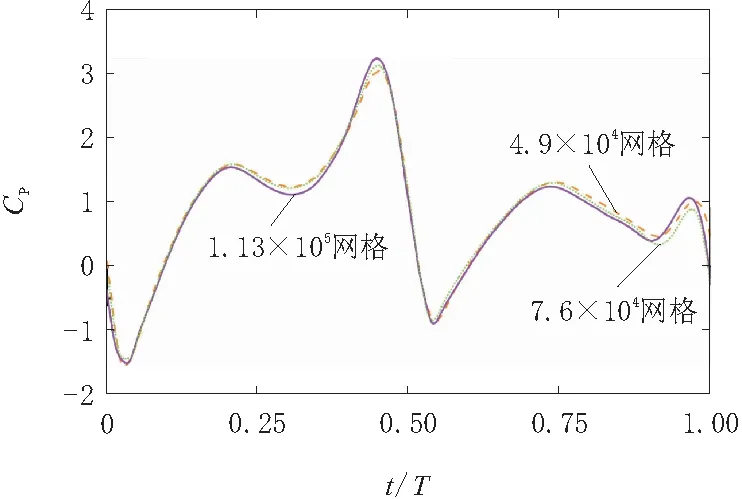
图3 不同网格划分下的CP曲线

2 数值结果与分析

2.1 能量采集特性

为了剖析非对称俯仰振幅振型对并联扑翼能量采集性能的影响,本文分别针对f=0.159 Hz时不同向内冲程俯仰振幅θin和向外冲程俯仰振幅θout下的扑翼不对称振荡过程展开研究。图4为多种非对称俯仰振幅振型下的平均功率系数曲线。由图4可知,当向内冲程俯仰振幅θin逐渐增大时(即θout=70°曲线),扑翼的平均功率系数先增大后减小,最优采集性能出现在θin=80°,θout=70°的振型下,此时CPm为0.828。与对称振型(θin=θout=70°)相比,采用非对称振型使CPm提升约14.25 %。这说明合理采用向内、向外冲程的非对称振荡模式能够有效提升扑翼能量采集性能。随着向外冲程俯仰振幅θout逐渐增大(即θin=70°曲线),CPm曲线同样表现出先增大后减小的变化趋势,这说明合理增大俯仰振幅能一定程度上提高扑翼的能量采集性能,但俯仰振幅过大时会因为在沉浮极限位置附近较大俯仰速度引起扑翼能量消耗,导致CPm不增反降。

图4 不同非对称俯仰振幅振型下CPm的变化曲线

扑翼采集效率η是衡量其能量采集性能的重要指标之一。图5展示了不同非对称振型下采集效率的变化曲线。可以看到,不同俯仰振幅振型下扑翼的采集效率变化曲线与平均功率系数曲线趋势基本一致,最大效率出现在θin=80°,θout=70°振型下,此时η=0.414。

图5 不同非对称俯仰振幅振型下η的变化曲线

根据前期对扑翼能量采集机理的研究[12]发现,扑翼主要通过沉浮振荡过程完成对来流能量的采集。图6展示了并联扑翼在多种非对称振型下通过沉浮振荡所采集能量CPhm的变化曲线。由图6可知,随着俯仰振幅的增大,CPhm先增大后减小,沉浮振荡过程的最佳能量采集性能出现在θin=80°,θout=70°振型时,此时CPhm=0.968,约为最差采集性能(θin=50°,θout=70°振型)的2倍。也就是说,通过控制并联扑翼的振荡振型能够较大提升其沉浮振荡过程的能量采集性能。图7所示为θout=70°时不同俯仰振幅振型下升力系数Cl的变化曲线。可以看到,随着θin的增大,翼型所受气动升力明显增大。这是因为随着俯仰振幅增大,扑翼俯仰角速度逐渐增大,对翼型表面涡的形成和脱落具有促进作用,有利于形成更大的气动升力,进而提升了沉浮振荡采集性能。当俯仰振幅增大到一定程度时CPhm开始下降,这是大俯仰角速度下扑翼在沉浮极限位置处调整振荡姿态需要消耗更多能量导致的。

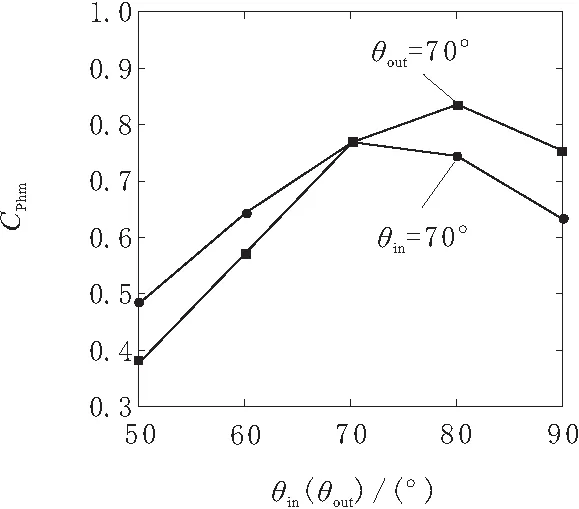
图6 不同非对称俯仰振幅振型下CPhm的变化曲线

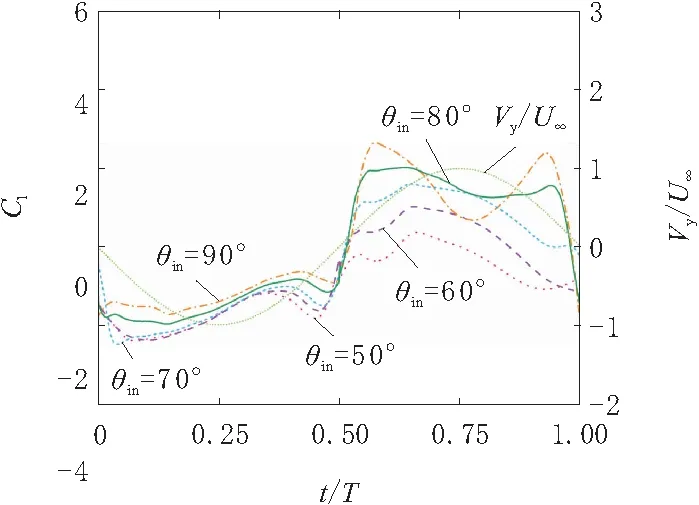
图7 θout=70°时,不同非对称俯仰振幅振型下Cl的变化曲线

2.2 流场分析

在振荡过程中,并联扑翼表面会因其振荡姿态变化形成涡结构,涡结构的演变和脱落与翼型采集特性紧密相关。图8分别展示了扑翼在向内冲程和向外冲程不对称振荡的θout=70°、θin=80°振型,θout=80°、θin=70°振型,θout=60°、θin=70°振型下的流场涡量云图。由图8可知,在t/T=0时刻,扑翼表面涡结构位于翼型中部和尾部,尾缘涡即将在来流作用下脱落。以图8a所示工况为例,随着扑翼向外冲程运动,翼型压力面首先发生流动再附(t/T=0.1～0.2区间),之后在吸力面出现新的前缘涡(t/T=0.3时刻)。此后,前缘涡在振荡运动和来流的共同作用下尺度逐渐增大并向尾缘移动,在t/T=

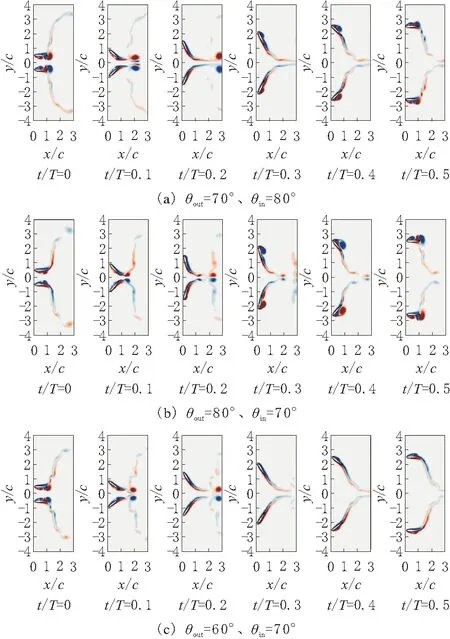
图8 不同非对称俯仰振幅振型下并联扑翼的流场涡量云图

0.5时即将脱落。结合图7所示升力系数变化曲线可知,脱落涡会引起翼型所受升力发生明显波动。

由图8可知,扑翼向外冲程俯仰振幅θout越大,翼型在向外冲程过程中前缘涡出现的时刻越早,涡发展越成熟,尾缘涡尺寸越大。结合图8b、图8c和图4所示功率系数曲线可知,在向内冲程俯仰振幅θin相同时,更大的向外冲程俯仰振幅具有更大的有效攻角,所形成的脱落涡尺寸更大,产生更大的气动升力,进而显著提升并联扑翼的平均功率系数。

为进一步剖析不对称振荡过程中涡的形成和演变规律,以θout=70°、θin=80°振型为例对其压力场演变过程进行分析,如图9所示。结合图8可知,在振荡起始时刻(t/T=0),并联扑翼由于结构特点两扑翼尾缘涡相距较近, 在翼型中后部形成较大的低压区域,有利于产生更大的气动升力和能量采集效果,这也是并联扑翼结构性能优于传统单扑翼结构的原因之一。t/T=0.1时,并联扑翼形成收缩通道,对流体具有一定的阻碍作用,出现压力较大的区域,压力面流体发生流动再附;t/T=0.2时,翼型吸力面前缘出现低压区域,这是前缘涡出现的萌芽状态,随后在沉浮俯仰耦合振荡过程中,该低压核心区域范围和强度增大,并逐渐向翼型尾缘移动,翼型吸力面出现流动分离现象。当扑翼运动到沉浮极限位置处,翼型表面更大范围的低压区域对应着充分发展并且即将发生脱落的涡结构,翼型因两侧压差形成气动升力,进而实现来流能量采集。