稳定跟车状态驾驶风格识别及迁移特性
2023-10-08彭金栓赵文超
彭金栓,赵文超,刘 潞,刘 通,张 磊
(重庆交通大学 交通运输学院,重庆 400074)
0 引 言
据统计,85%左右的道路交通事故与驾驶人因素有关,且所有的事故形态中,大约有1/4~1/3的道路交通事故和90%的高速公路事故是由于自车追尾前车而引起[1]。追尾碰撞作为最常见的跟车事故类型,已成为道路交通事故重要诱因之一。跟车是一个动态、复杂的过程,直接影响道路通行能力及效率,且与道路交通安全密切相关[2]。相关学者针对跟车过程阶段划分进行了研究。徐进等[3]基于实车试验对跟车过程中车头时距和车头间距进行分析,将车辆的跟车状态划分为强跟驰、过渡阶段、弱跟驰3种状态;郭景华等[4]采用相关系数法分析了跟车间距、相对速度等因素,将跟车工况分为3种;H.OZAKI[5]基于实车数据对跟车模型参数进行标定,且将跟车过程划分成加速、稳定、减速3个阶段;袁伟等[6]通过相对速度作为分界点将跟车阶段分为加速、稳定和减速3个阶段;G.MARSDEN[7]对跟车阶段进行划分,并将相对速度位于±1.5 m/s之间的数据定义为稳定跟车阶段。
驾驶风格作为驾驶行为评价研究的重要组成部分,是指驾驶人的驾驶习惯或长期养成的模式较为固定的驾驶方式[8]。驾驶风格一般可分为保守型、一般型和激进型,且激进型驾驶人发生交通事故的概率是一般型驾驶人的4倍以上[9]。因此,亟需针对不同驾驶风格的识别和划分开展研究。现今关于驾驶风格的研究主要包括问卷调查、驾驶模拟器、实车试验3种研究方法[10]。驾驶人填写问卷时,可能会出现高估或低估自身技术水平,难以保证自评结果的可靠性[11]。亦有借助驾驶模拟器开展的相关研究[12],不过存在驾驶体验真实感与现实不符、仍与驾驶人的实际驾驶操作区别较大等不足。此外,WANG Wenshuo等[13]通过开展实车试验,对不同风格驾驶人进行识别与划分。此类研究基于实车试验数据分析,所得驾驶人分类结果可靠性更高,更能真实反映驾驶人实际驾驶过程中的行为特点与个性化驾驶特征。因此,笔者通过开展实车试验,并基于实车数据对驾驶风格进行划分及特性分析。
不少学者进一步针对驾驶风格识别与划分方法开展研究。Z.CONSTANTINESCU等[14]使用分层聚类及主成分方法对驾驶风格进行分析和划分;侯海晶等[15]基于K均值及主成分方法对驾驶风格进行聚类分析和类型划分;郝景贤等[16]采用K均值方法对混动汽车的驾驶风格进行聚类,并采用支持向量机识别划分结果;刘通等[17]基于实车数据,选取跟车时距和制动时距均值为聚类指标,基于K均值聚类结果的高斯混合模型将驾驶人划分为3种不同的驾驶风格;吴振昕等[18]基于K均值算法和D-S证据理论方法对所建跟车及换道模型进行聚类和验证;李立治等[19]使用3种聚类方法划分实车数据类型,并采用神经网络识别分类结果,样本识别率均为100%。
目前关于跟车及驾驶风格方面的研究虽然较多,但鲜有学者将驾驶风格与跟车过程中稳定跟车状态结合起来开展研究。因此,笔者基于高速工况下的实车试验数据,重点分析稳定跟车状态下驾驶人风格划分识别及特性分析,研究影响驾驶人稳定跟车指标及理解学习不同风格驾驶人的稳定跟车特性,可为高速工况下自动驾驶系统跟车预警及控制策略的设计与制定提供参考。
1 试 验
1.1 被试驾驶人
试验共招募20名驾驶人(8名女性驾驶人),驾驶人年龄范围为20~52岁,驾龄范围为1~28 a。试验时,被试驾驶人只需按照自己平时的驾驶习惯自然驾驶即可。
1.2 试验仪器
采用的VBOX传感器可通过CAN总线获得车辆速度、航向角等数据。陀螺仪用于获取车辆横向及纵向加速度。毫米波雷达用于探测前后车辆相对速度、距离及角度等。Mobileye车道线识别系统可获取车辆距离左右车道线边缘的距离及速度等信息。踏板开度传感器可获得车辆加速踏板开度数据。行车记录仪采集的视频信息可为驾驶人操作特征参数及车辆运动特征参数等数据筛选提供辅助验证。
1.3 试验路段
选取重庆市周边道路条件良好、交通流量适中、弯道较少且曲率较小的路段作为试验路线。试验路线由两段道路构成:城市内环快速道路和高速公路。其中,城市内环快速道路全长21 km(江南立交-南环互通,双向四车道),限速70~90 km/h;高速公路G75(巴南-綦江段,双向四车道)全程37 km,限速100~110 km/h。
1.4 跟车数据筛选
跟车数据筛选基于以下原则[6,17]:选择连续跟车时长大于10 s的跟车数据;由于笔者旨在分析车辆高速行驶时的稳定跟车状态,自车行驶速度不小于60 km/h;前后车距离区间为20~150 m。将跟车过程分为加速、稳定及减速3个阶段,如图1。
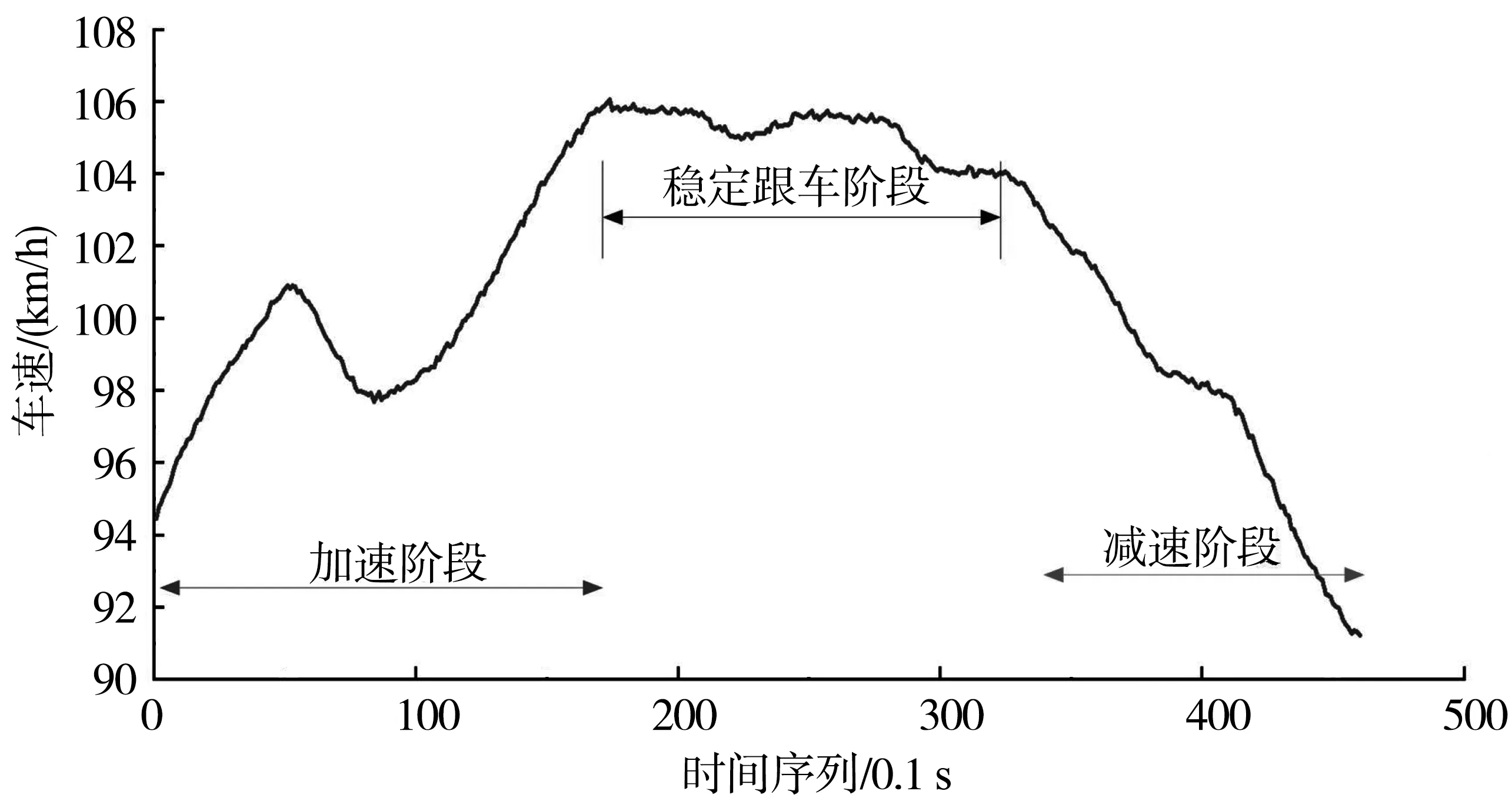
图1 跟车过程阶段划分
在加速阶段,自车车速不断增加直至接近或达到驾驶人期望车速,与前车距离不断缩小,达到驾驶人期望跟车距离。稳定跟车为相对距离接近驾驶人期望间距,相对速度及加速度等均处于较为稳定的阶段。跟车距离变小直至低于期望间距,自车会适当制动以保持安全跟车距离,此过程为减速阶段。笔者重点研究稳定跟车阶段。参考相关定义,选取相对速度为±1.5 m/s的跟车数据为稳定跟车事件[7]。通过筛选,共获取301段连续稳定跟车数据。
2 稳定跟车特性
跟车间距、跟车时距、碰撞时间(time to collision,TTC)均为常用的跟车行为分析指标。跟车间距过小易引发后车追尾,跟车间距过大则会减小快速路或高速路的容量,降低道路通行能力。跟车时距与跟车间距及自车速度有关,与自车驾驶行为关系密切,可为跟车行为特性研究提供参考。考虑到笔者重点分析稳定工况下的跟车特性,自车与前车相对速度差距较小,TTC值及变化范围均较大,故不将TTC作为文中跟车行为分析指标。
2.1 跟车间距与跟车时距
图2、图3分别为所有稳定跟车样本跟车间距及跟车时距的分布情况。从图2、图3中可看出,二者均基本符合正态分布特性,且分布频次最高的跟车间距为60~80 m,平均跟车间距为66.3 m;分布频次最高的跟车时距为2~3 s,平均跟车时距为2.65 s,且跟车时距大于6 s的样本较少。

图2 跟车间距分布
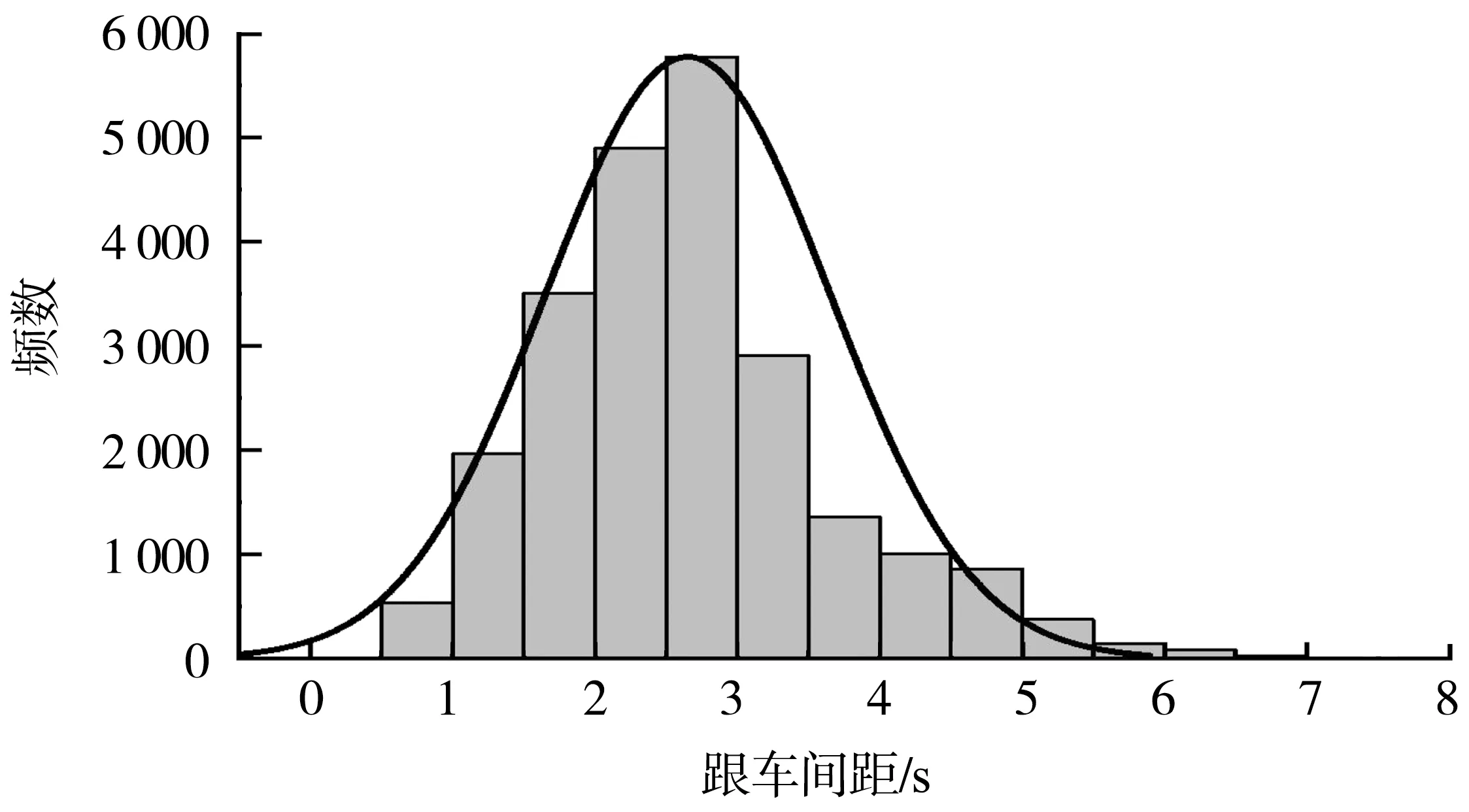
图3 跟车时距分布
2.2 自车速度
自车速度是车辆行驶过程中驾驶人易于感知、可体现驾驶风格的一种指标。谨慎保守的驾驶人往往会以较为稳定或接近自己的期望速度跟随前车,而冒进的驾驶人则会频繁变更车道或调整车速至与限速值较为接近的速度。稳定跟车样本自车速度分布情况如图4。
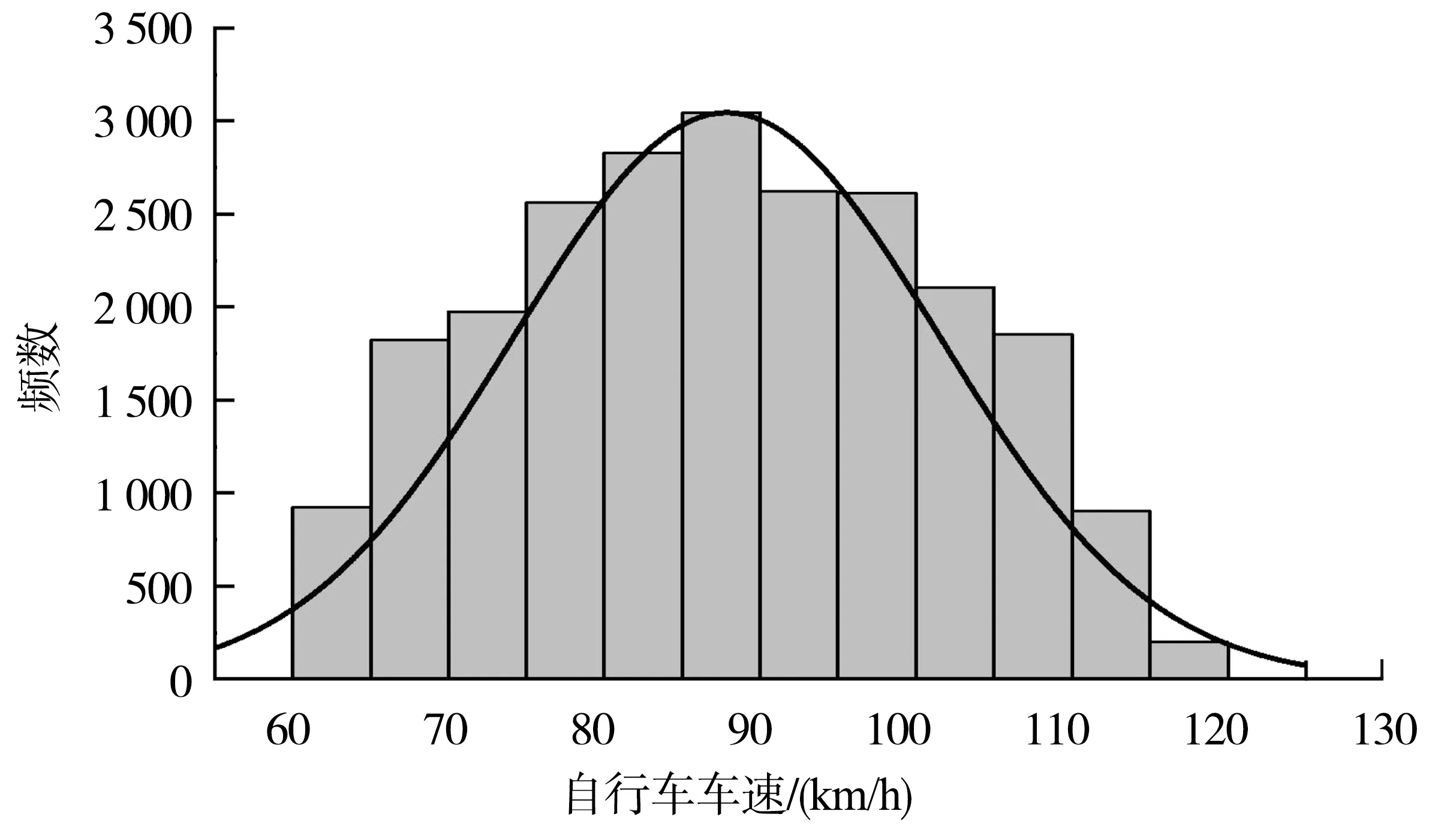
图4 自车速度分布
从图4可看出,自车速度分布频次最高的区间为70~100 km/h,平均速度为87.5 km/h。将自车速度按10 km/h的间隔划分为6个区间,进一步对各纵向指标在不同速度区间下的规律进行分析。
2.3 加速踏板开度与速度
加速踏板开度可直观反映速度控制情况,分析并统计各速度区间下的加速踏板开度分布(图5)。由图5可知,随着自车速度的增加,加速踏板开度均值亦呈现增加态势,符合日常驾驶规律。此外,使用单因素方差法对样本进行显著性检验,结果表明,不同车速区间加速踏板开度具有显著性差异(P=0<0.05)。表明随着车速提升,若要继续保持稳定跟车状态,须加大加速踏板开度以提高自车速度。

图5 不同速度区间加速踏板开度分布
2.4 跟车间距与速度
分别对不同速度区间下的跟车间距进行统计(图6),随着速度区间的提升,平均跟车间距也呈现增加态势。其中,70~80 km/h和80~90 km/h两个速度区间的平均跟车间距较为接近,而90 km/h及以上的速度区间的跟车距离增加较为明显。原因可能为自车速度相对较低时,驾驶人有足够信心保持更近的跟车距离,而车速较高时,驾驶人为保证行车安全通常选择增加跟车间距。此外,根据方差检验结果可知,不同速度区间跟车距离亦具有显著差异(P=0<0.05)。
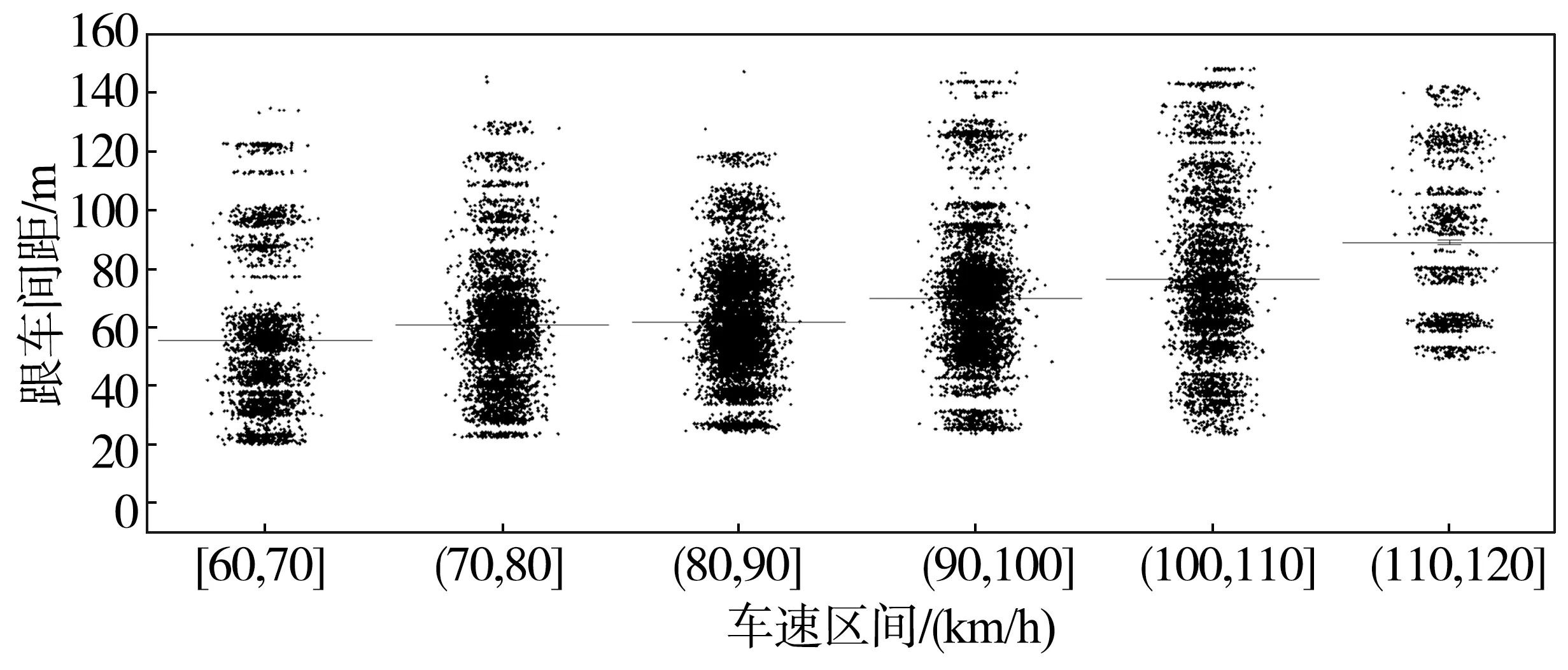
图6 不同速度区间跟车间距分布
2.5 跟车时距与速度
同样地,分析并统计各速度区间下的跟车时距分布(图7)。由图7可知,驾驶人跟车时距受速度变化的影响较小,表明高速行驶条件下驾驶人更愿与前车保持比较稳定的相对运动关系。此外,对样本进行单因素方差检验,结果表明,不同速度条件下跟车时距分布无显著性差异(P=0.095>0.05)。
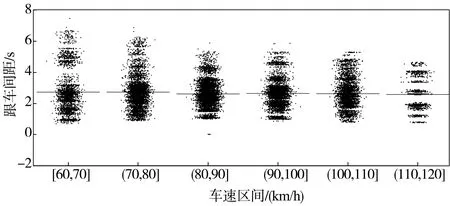
图7 不同速度区间跟车时距
3 驾驶风格分类识别
3.1 基于K均值的驾驶风格识别划分
通过选取合适的驾驶风格表征指标,使用K均值方法完成样本分类识别。跟车间距和跟车时距均可作为跟车行为分析指标,且加速踏板开度可间接表征稳定跟车过程中的速度及纵向加速度变化情况[20]。因此,笔者采用跟车时距、跟车间距和加速踏板开度作为表征驾驶人稳定跟车时的驾驶风格识别参数。
运用K均值聚类算法对301段稳定跟车事件进行聚类分析,根据已有研究,将20名驾驶人划分为保守型、一般型和激进型3类[17]。由于跟车间距、跟车时距及加速踏板开度3个指标量纲和单位不同,且跟车间距与其余2个指标数值大小差异较大,会导致其余2个指标在聚类时贡献度较低。因此,为消除差异性对K均值聚类造成的影响,先对3个指标进行z分数(z-score)标准化,z分数标准化公式如式(1):
(1)

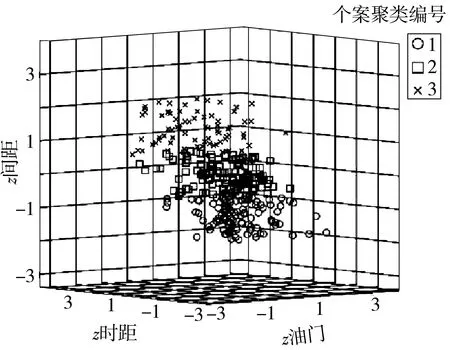
图8 K均值聚类结果
由图8可知,类型1属于激进风格,类型2属于一般风格,类型3属于保守风格。在此基础上,根据每个驾驶人驾驶样本中不同风格类型出现的频数及所占比例,按照隶属度最大原则将20名驾驶人划分为保守型(驾驶人序号:2、5、9、10、14、17)、一般型(驾驶人序号:1、4、6、12、13、15、16)和激进型(驾驶人序号:3、7、8、11、18、19、20)共3类。
3.2 决策树聚类结果验证及不同驾驶人跟车特性
进一步通过CART决策树对已有风格聚类结果进行可行性分析与验证,选用与K均值相同的聚类数目及输入指标进行数据决策与分类,结果如图9。CART决策树分类准确率达到99.7%,表明基于K均值的驾驶风格分类识别结果可行。在此基础上,分别对基于K均值得到的不同风格驾驶人稳定跟车特性及分布规律进行分析。
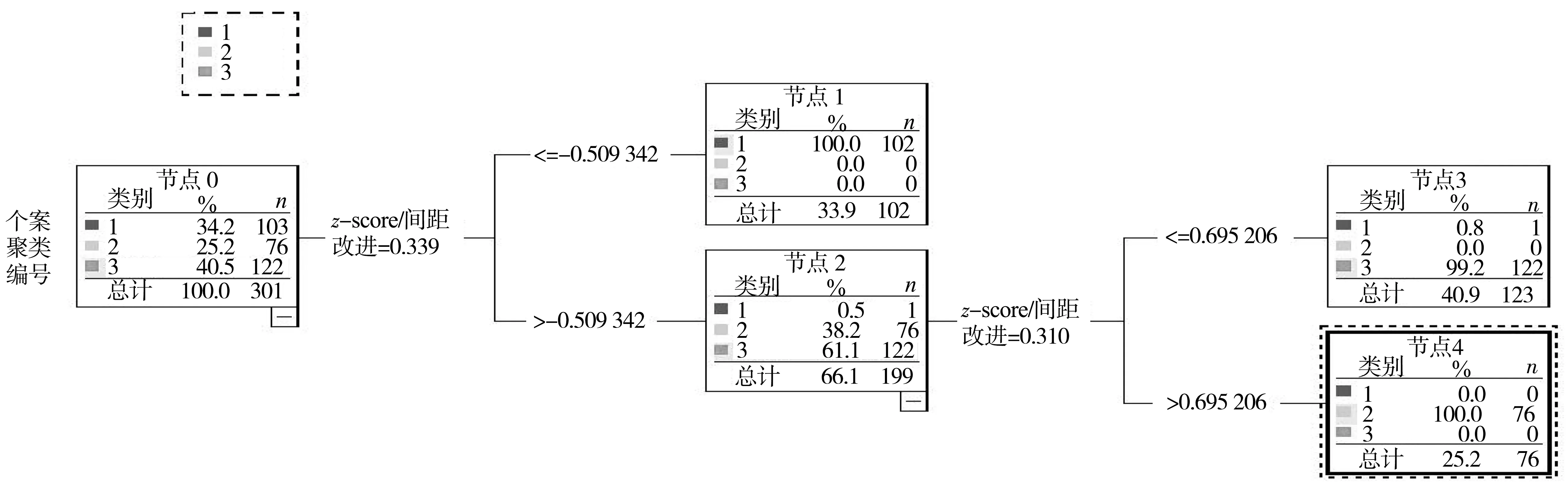
图9 CART决策树分类结果
3.2.1 加速踏板开度与速度
驾驶人通过加速踏板可直接控制和影响车速变化,3种风格驾驶人在稳定跟车过程中的自车速度及加速踏板开度分布情况如图10、图11。激进型驾驶人车速及油门踏板开度均值最大,一般型次之,保守型最小。进一步地,通过单因素方差检验可知,不同风格驾驶人的自车速度(P=0<0.05)及油门踏板开度(P=0.04<0.05)均存在显著性差异。

图10 不同风格驾驶人自车速度分布

图11 不同风格驾驶人油门踏板开度分布
3.2.2 跟车间距与跟车时距
考虑到试验数据是在高速行驶条件下且为稳定跟车状态下的数据,因此,跟车间距和跟车时距普遍较大。不同风格驾驶人跟车间距、跟车时距分布如图12、图13。由图12、图13可知,保守驾驶人跟车间距均值为97.2 m,一般型次之为76.5 m,激进型为61.1 m;跟车时距均值分别4.4、3.2、2.3 s。由此表明,激进型驾驶人通过更近的跟车间距来满足自己的心理需求,而保守型则会保持较远的跟车间距来保证行车安全。分别对其进行单因素方差及K-W检验可知,不同风格驾驶人跟车间距(P=0.00<0.05)及跟车时距(P=0.00<0.05)分布呈显著性差异。由此亦可反映,使用基于K均值算法对不同风格驾驶人的聚类效果良好。
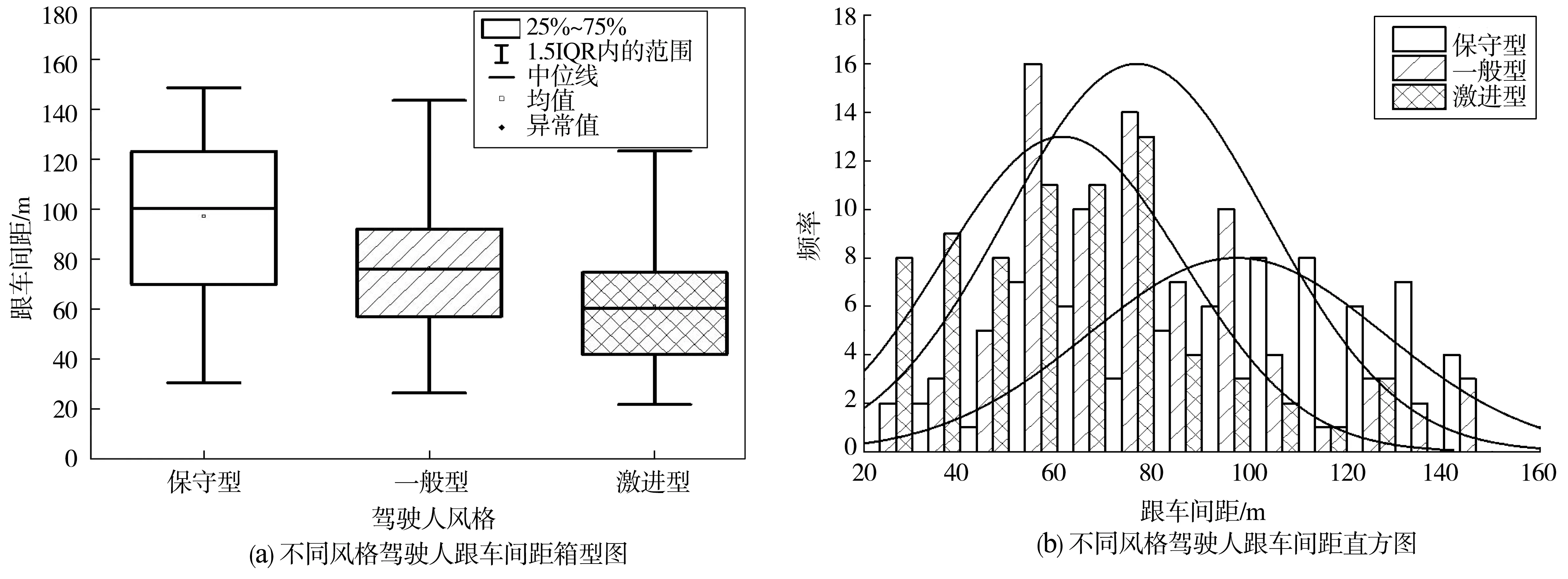
图12 不同风格驾驶人跟车间距分布
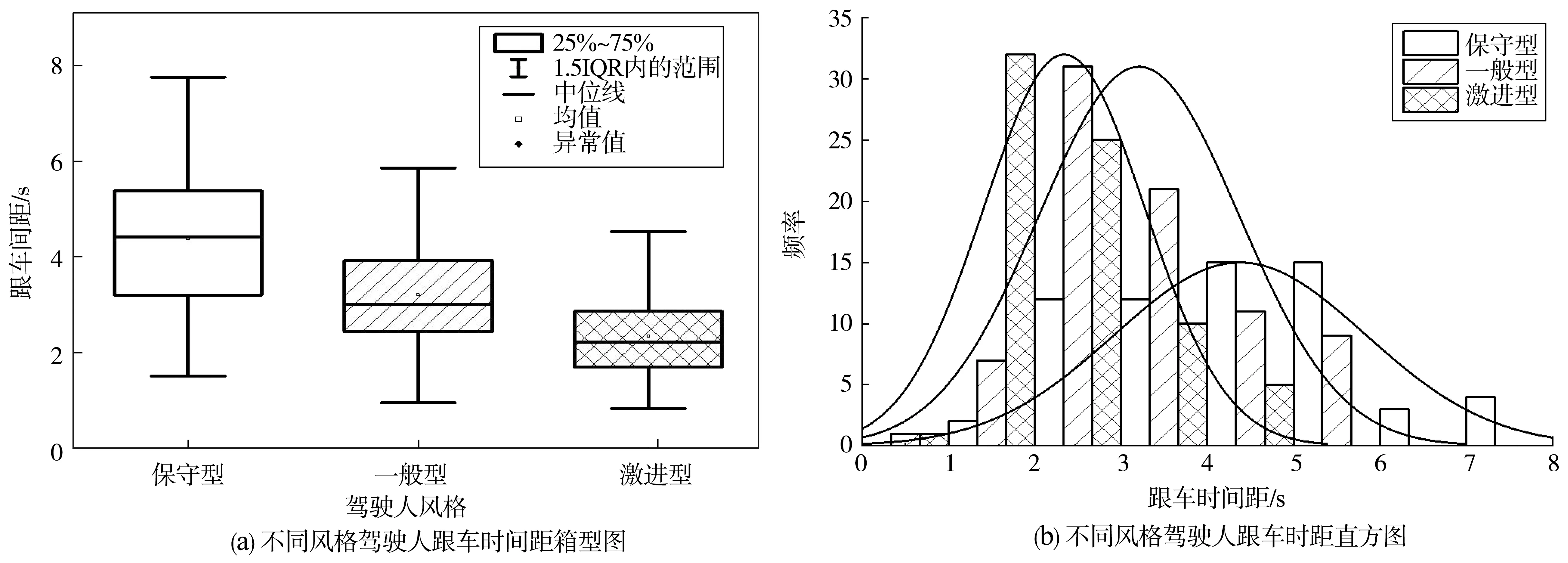
图13 不同风格驾驶人跟车时距分布
3.3 长时间稳定跟车驾驶风格迁移特性
实际行驶过程中,随着驾驶时间的持续增加,生理心理因素及周围环境的变化、驾驶人跟车风格是否会发生漂移是一项值得探析的假设命题。选取不同风格中具有代表性的3位驾驶人,对试验过程中驾驶人样本风格水平变化及偏向进行统计。数字1、2、3分别表示激进型、一般型及保守型。对驾驶人所有跟车样本的驾驶风格属性采取算术平均处理,基于时间序列将试验分为1(试验前半段)、2(试验中段)和3(试验后半段)共3个阶段,并计算各阶段风格水平均值(图14)。
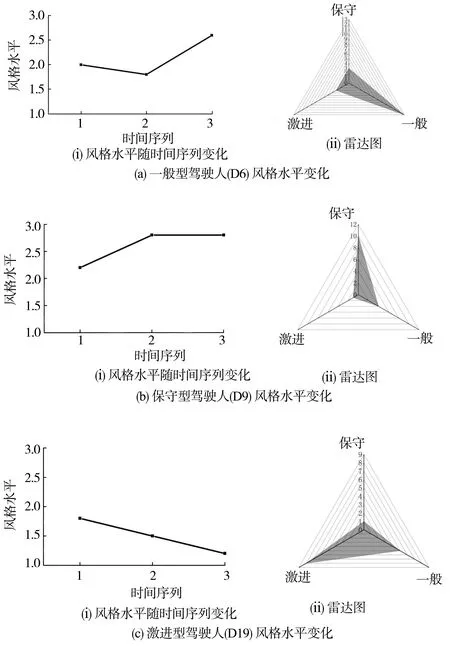
图14 长时间稳定跟车驾驶风格水平变化
图14中,风格水平位于1.0~1.5时风格偏激进,位于1.5~2.0时风格为激进偏一般,位于2.5~3.0时风格趋于保守,位于2.0~2.5时风格为保守偏一般。保守型驾驶人(D9)在试验初期为保守偏一般,随后逐渐趋于保守。激进型驾驶人(D19)在试验初期为激进偏一般,随后逐渐趋于激进。一般型驾驶人(D6)基本保持一般型驾驶风格,后半段试验过程中为一般偏保守。同样地,进一步统计3类驾驶人在3个试验阶段的驾驶风格算术平均数,如图15。可见,随驾驶时间序列推进,保守型驾驶人趋于保守;激进型驾驶人趋于激进;一般型驾驶人在整个试验过程中的表现相对较为稳定,在一般型风格附近波动,且随试验推进,呈现逐渐趋于保守的变化趋势。笔者对稳定跟车过程中的驾驶风格水平变化按时间序列划分为3个阶段进一步细化评估,针对不同数量规模及道路环境条件下采集的实车试验数据,亦可不局限于使用3个试验阶段的粗略分类。此外,长时间稳定跟车状态下的驾驶风格变化指数可为自动驾驶车辆实时动态识别周围驾驶人驾驶风格及驾驶意图预测等决策依据提供参考。

图15 驾驶人不同阶段驾驶风格水平变化
4 结 语
分析了稳定跟车状态下跟车时距、跟车间距和自车速度分布特性,以及不同速度区间下跟车时距、跟车间距和加速踏板开度的变化规律,发现随自车速度的提高,跟车间距与加速踏板开度均呈现增大的趋势,且在不同速度区间下均具有显著性差异。不同速度区间下的跟车时距均值则稳定分布于2.57~2.72 s,且无显著性差异。
将跟车间距、跟车时距和加速踏板开度作为聚类分析指标,基于K均值算法,计算不同风格类型频数及比例,将驾驶人划分为激进、一般及保守3种类型。使用CART决策树算法验证聚类结果,总体识别率为99.7%。
分析了不同风格驾驶人的油门踏板开度、跟车距离与时距分布规律。发现不同风格驾驶人在稳定跟车过程中跟车间距、跟车时距、自车速度、加速踏板开度共4项驾驶指标的分布均存在显著差异。通过分析稳定跟车阶段驾驶风格的迁移特性,发现随时间推移,激进型驾驶人趋于激进,保守型驾驶人更加保守,一般型驾驶人风格变化相对较为稳定。
文中研究方法和分析结果对稳定跟车状态下的驾驶风格识别与迁移特性分析具有一定的理论意义,可为自动驾驶汽车对周围驾驶员驾驶风格识别和车辆行驶轨迹预测提供理论依据。不过由于所选试验路段路况相对较好,无法体现不同行车场景下的稳定跟车特性,且被试驾驶人数量相对较少,有待进一步招募更多驾驶人进行模型验证。
