重载曲线缓和段钢轨滚动接触疲劳机理

栗杨，白彬亨，莫日格吉勒，赵鑫，温泽峰，王卓

(1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.内蒙古包钢钢联股份有限公司 制造部，内蒙古 包头 014010；3.中国铁路呼和浩特集团有限公司 工务处，内蒙古 呼和浩特 010000)

重载铁路曲线钢轨滚动接触疲劳(rolling contact fatigue, RCF)是世界性问题[1].在重载铁路钢轨由热轧升级为热处理材质的过程中，RCF加重现象[2]是轮轨系统不同步升级引发的问题[3-4].某重载铁路曲线轨道的现场调研表明[5]，圆曲线段钢轨的RCF最严重，在缓和曲线段上的RCF逐渐减轻直至消失，但入/出缓和段的RCF存在显著差异.本研究旨在展示此差异现象，为全面阐明重载曲线钢轨RCF机理奠定基础.

外曲线钢轨RCF研究多针对圆曲线段开展，缓和曲线段这一重要过渡部分的RCF研究匮乏.通过现场调研，Zhou等[6]发现钢轨磨耗速率增加，可减缓某重载铁路上曲线半径R=500～600 m圆曲线段外轨轨距角鱼鳞纹的发生；周清跃等[7]发现钢轨RCF集中发生在某重载铁路R≤800 m圆曲线段上，表现为外轨轨距角裂纹及剥离掉块和内轨轨顶中心裂纹，建议对应铺设合适等级钢轨并辅以预防性打磨；Matsuda等[8]发现某重载铁路R=800～1 800 m圆曲线段发生钢轨RCF，并伴有剥离.截取某重载铁路R=800 m圆曲线段U75V材质钢轨，寇沙沙等[9]的金相分析表明，外轨RCF区内伴有明显的剪切塑性变形.在JD-1轮轨模拟试验机上，钟雯[10]开展不同材质钢轨对比试验，发现抗疲劳性能更优的U71Mn材质适于磨损轻微的高速铁路，硬度更大的U75V材质适合磨损严重的重载铁路.模拟研究也广泛见于文献，焦彬洋等[11]通过轮轨静态接触模拟发现，过低的轨底坡会加剧轨距角鱼鳞纹，轨距加宽、黏着系数提升及钢轨预打磨可有效抑制其萌生与发展；梁喜仁等[12]模拟解释了某地铁R≤2 000 m圆曲线段外轨轨距角与内轨轨顶RCF；徐万华等[13]分析了钢轨廓形对重载铁路R≤800 m圆曲线段钢轨RCF的影响.

本研究以某重载铁路缓和曲线段的钢轨RCF为对象，展示R=580～1 000 m曲线入/出缓和段钢轨RCF差异，建立包含机车、货车的重载列车动力学模型，预测实际轮轨廓形匹配下的列车曲线通过行为，并利用损伤函数，揭示研究对象曲线入/出缓和段钢轨RCF差异的萌生机理.

1 入/出缓和曲线段现场观测

现场观测某轴重25 t运煤重载铁路，R=580 m曲线外、内轨均于2022年3月上道并于同年4月进行预打磨，曲线入/出缓和段的轨面状态如图1所示，选取位置均为超高62 mm处.由图1(a)可见，入/出缓和段外轨接触光带内存在2个疲劳区，且出缓和段伴有肉眼可见的剥离，但未见于入缓和段，即出缓和段滚动接触疲劳更严重；由图1(b)可见，内轨仅在轨顶中心处存在1个疲劳区，较相应外轨轻微，但出缓和段疲劳更严重的问题同样存在.

图1 某轴重25 t运煤重载铁路上某半径580 m曲线入/出缓和段超高62 mm处的钢轨表面状态对比Fig.1 Rail surface condition at 62 mm superelevation in entering/leaving transition section of R=580 m curve on 25 t axle load heavy haul railway

如图2所示为R=580 m曲线的分段示意图，圆曲线段超高为75 mm，其中圆缓点表示圆曲线与缓和曲线的交汇处，直缓点表示直线与缓和曲线的交汇处.如图3所示为使用涡流探伤仪测得的不同超高处外、内轨轨面裂纹深度峰值结果.图中，L为缓和曲线上测量位置到直缓点的纵向距离，c为裂纹深度峰值，h为测量位置的外轨超高；纵向距离与超高间关系为三次抛物线方程[14].在R=580 m曲线整个缓和段内，相同超高处的出缓和段轨面裂纹深度始终高于入缓和段，这与现场肉眼观测的出缓和段疲劳更严重的事实一致.

图2 半径580 m曲线入/出缓和段以及圆曲线段示意图Fig.2 Schematic diagram of entering/leaving transition section and circular section for R=580 m curve

图3 半径580 m曲线入/出缓和段不同超高处测量的轨面裂纹深度峰值Fig.3 Peak crack depth of rail surface measured at different superelevations in entering/leaving transition section of R=580 m curve

如图4所示为同一线路另外2条曲线上入/出缓和段的钢轨表面状态对比，半径分别为800、1 000 m，选取位置的超高分别为72、40 mm（圆曲线段超高分别为80、50 mm），外、内轨于2019年4月上道，并在2022年4月进行修复性打磨.篇幅限制，仅展示外轨.对比图1发现，随着曲线半径增大，入/出缓和段同一超高饱和度（实际超高与圆曲线段超高的比值）处附近的外轨RCF逐渐减轻，R=800 m和R=1 000 m曲线外轨轨面的疲劳区数量降为1个，且轨面剥离正趋于消失，但疲劳差异依然存在.

图4 相同重载线上不同半径曲线入/出缓和段外轨表面状态Fig.4 Rail surface on same heavy haul line with different radius curves entering/leaving transition section

钢轨RCF与轮轨廓形密切相关[15]；测量R=580、800、1 000 m曲线缓和段，圆曲线段不同超高处的钢轨廓形；随机测量运行于该重载线上的主力机、货车车轮廓形.考虑超高，绘制圆曲线段钢轨廓形测量结果对比如图5所示，z1、z2分别为外轨、内轨廓形的测量结果.某型8轴大功率电力机车和主力货车各一个转向架的车轮廓形测量结果如图6所示.图中，y为钢轨横向位置，w1、w2分别为机车、货车车轮廓形的测量结果.所调研机、货车车轮磨耗均不严重，且现场服役车轮状态普遍如此，同时上述线路均采用60 kg/m的U75V淬火钢轨且上道后均被打磨为60N廓形.所调研重载线路的轨距、枕距以及超高等参数均维护良好，枕木、道砟均保持着良好的使用状态，说明本研究关注的钢轨疲劳差异与R=580、800、1 000 m曲线轨道几何状态相关性不强.如图7所示，测取R=580 m曲线的轨道轨向、高低不平顺，其中A1、A2分别为轨向、垂向不平顺的测量结果，采样间隙为0.25 m.

图5 不同半径曲线圆曲线段实测钢轨廓形对比Fig.5 Measured rail profiles in curves with different radii

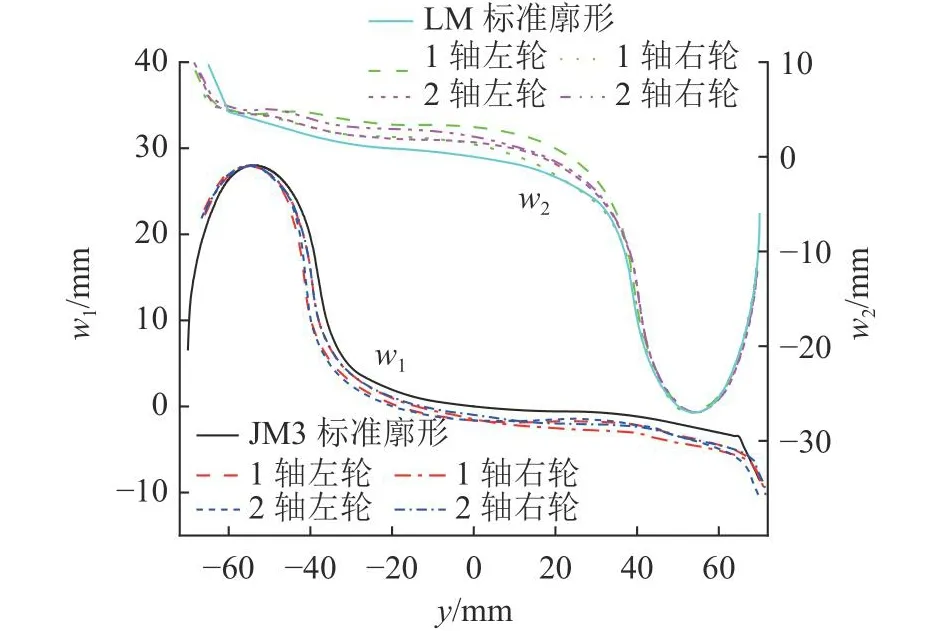
图6 运行于所调研重载线的机、货车车轮廓形随机测量结果Fig.6 Random measurements of locos and wagons running on investigated line

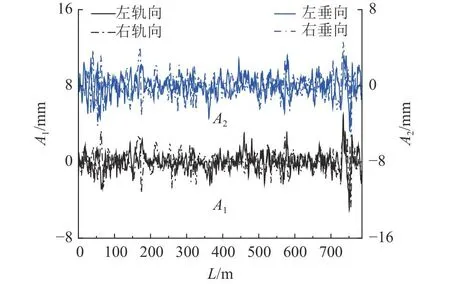
图7 某半径580 m曲线入/出缓和段与圆曲线段的实测轨道不平顺Fig.7 Measured track irregularity of entering/leaving transition section and circular curve section of R=580 m curve

2 钢轨滚动接触疲劳预测模型

2.1 列车曲线通过模型

2021年底，重载线上主力机车由轴重21 t功率7 200 kW的6轴电力机车全部更换为轴重25 t功率9 600 kW的8轴电力机车，牵引轴重25 t运煤专列货车以108节编组形式为主.因此，图1、3所示的状态（2022年5月）均可被认为是8轴机车（2节内重联）牵引的运煤专列作用的结果.针对所调研重载线上运行的108节货运运煤专列，在Simpack环境中建立包含2节机车和1节货车的列车动力学模型，如图8所示.机车子模型由1个车体、2个构架和4个轮对等组成，共54个自由度，货车子模型由1个车体、4个侧架、4个轮对、承载鞍及摇枕等组成，共68个自由度.机车与机车、机车与货车间车钩以图8中所示力元模拟[16].车体与转向架之间由二系悬挂连接，转向架与轮对间则由一系悬挂连接，相关弹簧和减振器等元件均由力元模拟，机车、货车设计参数如表1所示.表中，m为质量，J1、J2、J3分别为轮对、构架、车体的转动惯量，E1、E2分别为一系、二系悬挂刚度.引入现场实测轮轨廓形与轨道不平顺数据，未直接建模的107节货车以等效总阻力Fb的形式施加于货车模型尾部车钩处.考虑现场实际，模拟工况均假设匀速通过，即机车牵引力与列车总阻力平衡，具体施加方法见文献[17].其中，Fa、Ft分别表示单台机车与单节货车所受的总阻力，Ft为后接107节货车总阻力的等效.R=580、800、1 000 m曲线的相关几何参数如表2所示，速度v由现场测量得到，其他参数则取自线路LKJ系统（列车运行监控装置），p为线路坡度，L1、L2分别表示缓和曲线与圆曲线长度.3条曲线日通过总质量为5.0×105t，同时曲线均处于相邻区段内且非靠近车站，意味着其列车通过车次、速度及重量相同，这是本研究仿真工况的前提.模拟中线路均假设为左曲线，缓和曲线采用三次抛物线型[18]设计，即缓和曲线任意位置处超高h（s）与其距离直缓点纵长s间关系为

表1 机车与货车动力学模型建立所用主要参数Tab.1 Main parameters used for establishing dynamic models of locos and wagons

表2 模拟曲线的主要参数Tab.2 Main parameters of simulation curves

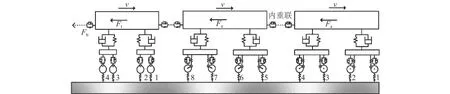
图8 列车动力学模型示意图Fig.8 Schematic diagram of train dynamics model

式中：h1、h2分别为最小与最大超高，分别对应图2中直缓点与圆缓点的超高；直线段超高为0，因此取h1=0，h2为所测圆曲线段超高值.

2.2 损伤函数模型

基于列车动力学预测结果，使用损伤函数模型[19]预测钢轨滚动接触疲劳的萌生.损伤函数主变量为磨耗数：

式中：Tx、Ty分别为纵、横向的轮轨蠕滑力，γx、γy分别为纵、横向的蠕滑率.如图9所示，假设损伤函数的疲劳发生门槛值FA和磨耗发生门槛值FB与硬度正相关，且损伤速率（图中折线斜率）不随材质变化，则U75V淬火钢（平均硬度H=369 HB）[20]的损伤函数模型关键参数由英国BS11钢（H=240 HB）相应取值[21]正比例得到.图中，D为车轮单次通过钢轨产生的损伤，Nf-1为车轮通过转数的倒数，当计算损伤量累计达到1时，意味着裂纹萌生.2种钢轨材料损伤函数的关键参数如表3所示.表中，ε1、ε2分别为裂纹萌生速率与磨耗速率.不同材质钢轨的损伤函数拓展方法，源自其发明者的推荐[19]，其适用性有待深入研究，本研究围绕不同工况下的对比分析开展，不过分关注预测的绝对数值.

表3 2种钢轨钢材料的损伤函数关键参数Tab.3 Main parameters of damage function of two rail steel materials

图9 2种钢轨钢材质的损伤函数示意图Fig.9 Schematic diagram of damage function of two rail steel materials

在模拟曲线上，纵、横向蠕滑力的大小可比，在滚动接触疲劳具体计算中，不再假设纵向蠕滑力与车轮滚动同向时裂纹不扩展[22]，即任何方向的蠕滑力均可导致滚动接触疲劳.损伤函数预测的不同车轮导致的总损伤，按照文献[23]介绍的方法，离散到轮轨接触斑内，叠加得到滚动接触疲劳在钢轨表面上的损伤分布.离散时，设置空间离散尺寸为0.1 mm，时间积分等效为沿纵向几何积分，即将短时内稳态损伤分布的假设隐含.

3 滚动接触疲劳预测结果

基于钢轨滚动接触疲劳预测模型，预测列车通过表2中不同半径曲线时外、内轨的RCF损伤.机车所致损伤为2台机车单侧所有车轮所致损伤之和，货车所致损伤为模型中货车单侧各车轮所致总损伤的108倍，即忽略各货车之间的差异.

3.1 半径580 m曲线

3.1.1 滚动接触疲劳萌生 如图10所示为重载列车通过半径580 m曲线时，外、内轨RCF的损伤预测云图.圆曲线段结果仅展示与缓和曲线等长的中间一段.图中灰色区域表示预测未发生滚动接触疲劳（损伤值为零），彩色区域为预测RCF发生区，横向零值表示轨面中心，轨面任意位置处损伤值为列车所有轮对通过时所产生RCF损伤值的代数和.动力学模拟的时间步长取0.02 s，速度67 km/h对应移动距离为0.37 m，制图时，假设任意2个连续时刻间的钢轨损伤保持不变，即与前一时刻结果一致，实现结果连续化展示.由图10中外轨结果可见，随着入缓和段内超高的不断增加，RCF从无到有，并逐渐增至圆曲线段内近似稳定波动的损伤分布，最大值为1.5×10-4Nf-1，到出缓和段RCF又逐渐降低直至为零.同时，相较入缓和段，出缓和段发生RCF的区域纵向更长，且相同超高处的疲劳严重程度明显更高.以超高62 mm处为例，入缓和段2个疲劳区的损伤峰值分别为2.4×10-6、5.6×10-5Nf-1，出缓和段各自为2.5×10-6、7.1×10-5Nf-1，即出缓和段疲劳损伤更严重，这一预测结果与图1(a)中所示现象吻合.在超高62 mm处，入缓和段外轨疲劳区的横向范围预测为[-27, -3]mm，出缓和段相应为[-23, -1]mm，这分别与图1(a)中[-26, -2]、[-24, 1]mm疲劳区范围吻合.由图10中内轨疲劳损伤云图可见，疲劳损伤量变化与外轨呈现出相同的趋势，圆曲线段内轨的疲劳区稳定在轨顶中心处，最大疲劳损伤量为1.3×10-4Nf-1，略低于外轨.

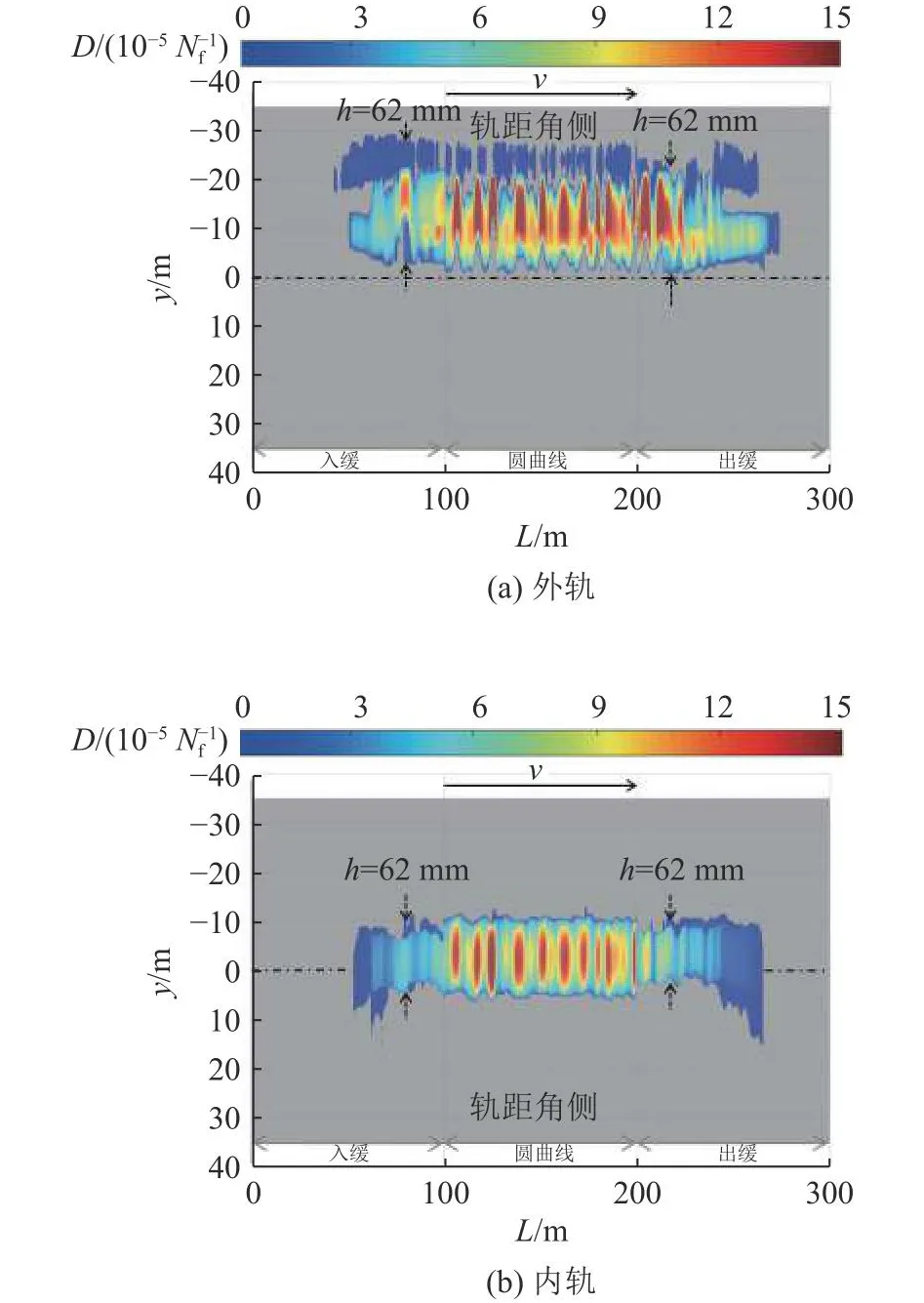
图10 半径580 m曲线外、内轨滚动接触疲劳损伤值预测结果Fig.10 Prediction of rolling contact fatigue value of R=580 m curve in high and low rails

入/出缓和段外、内轨疲劳区分布及疲劳严重程度差异等现象，均与观测现象吻合（例如图1）.为了清晰展示入/出缓和段的钢轨疲劳损伤差异，绘制R=580 m曲线缓和段每一横截面内的预测疲劳损伤峰值随纵向位置的变化图如图11所示.可以看出，出缓和段外、内轨疲劳损伤量总是高于入缓和段，且出缓和段的疲劳区纵向更长.具体而言，入、出缓和段外轨分别在25、14 mm超高处开始出现RCF损伤，内轨RCF损伤对应的纵向萌生位置分别为32、26 mm超高处.预测结果所展现的入/出缓和段疲劳损伤差异及疲劳严重程度沿纵向的变化趋势，与图3中现场实测的入/出缓和段RCF差异及疲劳纵向变化趋势吻合，验证了本研究建立模型预测该线路钢轨RCF的精确性.如无特殊说明，本研究展示的RCF预测结果均对应真实轮轨廓形匹配与实测轨道不平顺.

图11 损伤函数预测的半径580 m曲线入/出缓和段外、内轨滚动接触疲劳纵向分布Fig.11 Longitudinal distribution of rolling contact fatigue in high and low rails of R=580 m curve entering/leaving transition section predicted by damage function

3.1.2 入/出缓和曲线段疲劳差异机理 将图10中的疲劳损伤结果按机、货车贡献分解，得到如图12所示的入/出缓和曲线段的疲劳损伤对比结果.由图可见，入、出缓和段的滚动接触疲劳损伤差异均由108节货车通过主导，前2台机车通过时对疲劳损伤差异的贡献可以忽略.鉴于外、内轨疲劳损伤差异的趋势基本相同，限于篇幅，机车所致损伤仅展示外轨的预测结果.将图12（b）中108节货车所致外轨疲劳损伤按转向架的导向（1、3轴）与非导向轮对（2、4轴）进行分解，结果如图13所示.由图可知，不管是导向轮对还是非导向轮对，对入、出缓和段的疲劳损伤差异均有贡献，但导向轮对疲劳损伤幅值的贡献明显更大，主宰入/出缓和段的钢轨RCF差异.由于前后转向架的导向、非导向轮对贡献的差异并不明显，因此展示其各自代数和.选取货车前转向架，通过上述曲线入/出缓和段时，导向（1轴）和非导向（2轴）轮对外轨侧磨耗数Tγ沿纵向的变化如图14所示，钢轨滚动接触疲劳模型关键参数FA、FB和FC示于图中.由图可知，无论导向、非导向轮对，出缓和段磨耗数均大于入缓和段，且出缓和段高于疲劳门槛值FA（Tγ=26 N）的范围纵向更长，意味着出缓和段的RCF更严重.入/出缓和段的RCF损伤差异主要由导向轮对贡献，其磨耗数在超高16 mm处增至门槛值FA，更高超高下不断增大，且均处于门槛值FA和FC之间的疲劳发生区，使得疲劳损伤值随超高增大呈递增.非导向轮对因磨耗数明显低于导向轮对，仅有缓和曲线中段区域的幅值略高于疲劳门槛值，因此对疲劳的贡献低，不是入/出缓和段RCF差异的主因.

图12 仅机、货车通过半径580 m曲线入/出缓和段时，预测钢轨滚动接触疲劳沿纵向分布Fig.12 Prediction of rolling contact fatigue along longitudinal direction when only locos and wagons pass through R=580 m curve entering/leaving transition section

图13 货车转向架导向、非导向轮对通过半径580 m曲线入/出缓和段时，外轨疲劳损伤的纵向分布Fig.13 Longitudinal distribution of high-rail rolling contact fatigue,when wagon leading and non-leading wheelsets pass through entering/leaving transition section of R=580 m curve

货车前转向架导向轮对（1轴）通过上述曲线入/出缓和段时，外轨侧蠕滑力/率沿纵向分布的结果如图15所示.由图可知，相同超高处，由于出缓和段的纵、横向蠕滑力/率均明显高于入缓和段，直接导致图14中入/出缓和段磨耗数差异，以及图13中滚动接触疲劳差异.综合对货车转向架导向轮对分析可知，磨耗轮轨匹配下货车通过小半径曲线时，转向架导向轮对在出缓和段上作用的蠕滑力、率均明显高于入出缓和段，使得出缓和段产生更大的磨耗数，最终导致出缓和段的RCF更加严重.非导向轮对的结果呈现类似的规律，但幅值明显低于导向轮对，对RCF差异的影响有限.

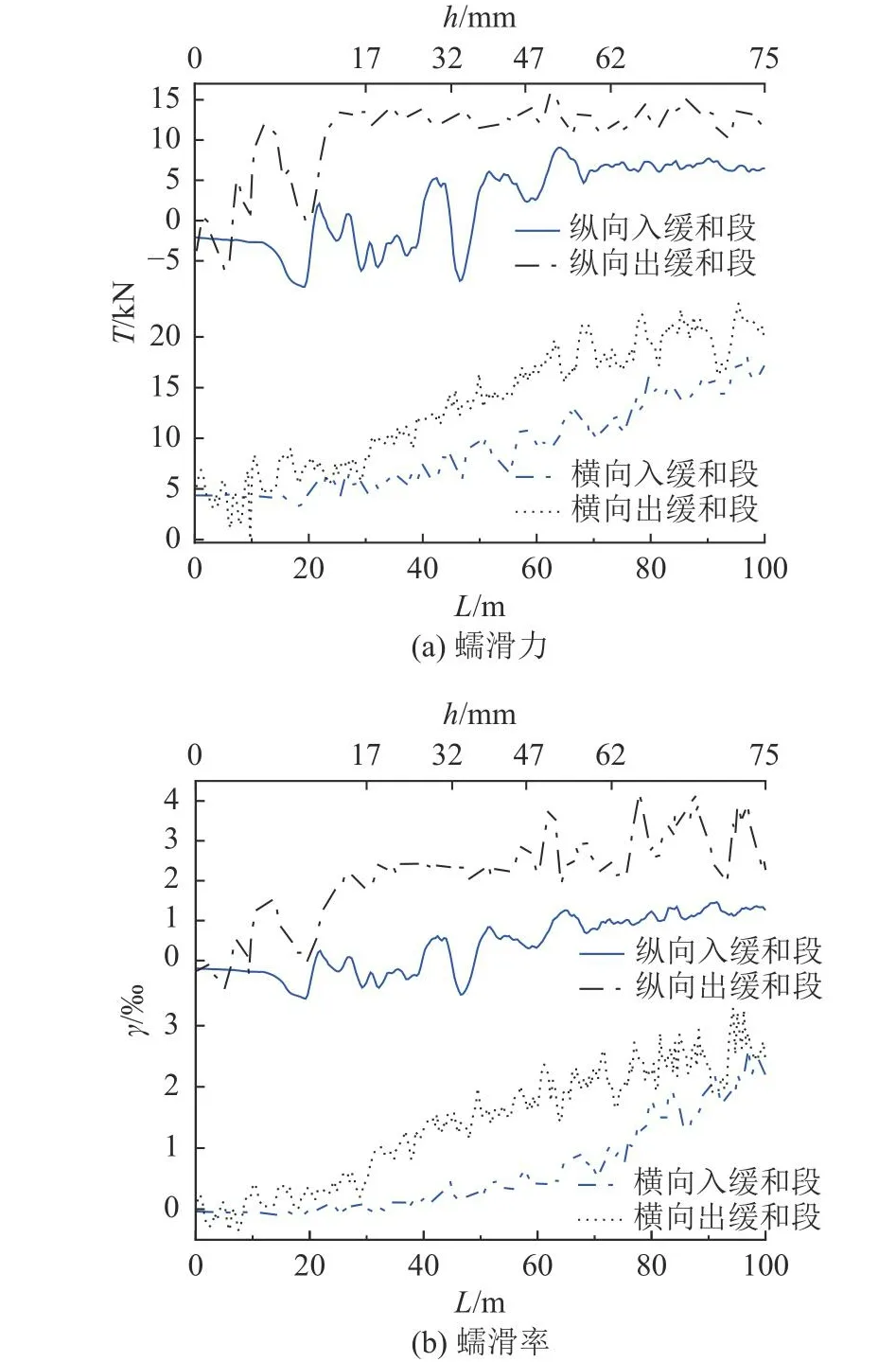
图15 货车前转向架导向轮通过半径580 m入/出缓和段时，外轨纵、横向蠕滑力/率绝对值的纵向分布Fig.15 Longitudinal distribution of absolute value of creep force and creep rate of high rail, when front bogie leading wheelsets of wagon passes through R=580 m entering/leaving transition section

3.2 轮轨廓形对疲劳差异的影响

由于轮轨磨耗失形会直接影响蠕滑力/率和滚动接触疲劳损伤[24]，仍以R=580 m缓和曲线段为例，进一步考虑磨耗轮-标准轨、标准轮-磨耗轨及标准轮-标准轨3种匹配条件，分析其对入/出缓和段滚动接触疲劳差异的影响.所调研线上机车与货车车轮对应标准轮为JM3廓形与LM廓形，钢轨对应标准轨为60N廓形.整列车通过后，入/出缓和段外轨RCF损伤差值沿纵向的分布如图16所示.定义疲劳损伤差值为相同超高处，出缓和段与入缓和段上的RCF损伤峰值之差.可见，磨耗轮-标准轨匹配工况的预测结果与磨耗轮-磨耗轨大致相同，标准轮-磨耗轨与标准轮-标准轨匹配工况的预测结果接近，但预测疲劳差的幅值明显低于前2个工况.在标准轮-标准轨匹配工况下，入/出缓和段钢轨的RCF损伤差值在零值上下波动，原因是模型中这2段考虑的不同轨道不平顺造成的轮轨蠕滑力/率波动差异，其对滚动接触疲劳的影响显然不及车轮磨耗失形.综合不同轮轨廓形匹配的滚动接触疲劳结果可知，在标准轮-标准轨匹配工况下，入/出缓和段的轮轨滚动接触和疲劳损伤行为无显著差异，随着车轮廓形因磨耗不断演化，逐渐出现入/出段钢轨RCF差异.

图16 不同轮轨廓形匹配工况下，半径580 m曲线外轨侧的入/出缓和段滚动接触疲劳损伤差值Fig.16 Difference of rolling contact fatigue of entering/leaving transition section of high rail of R=580 m curve under different wheel-rail profile matching conditions

3.3 曲线半径对疲劳差异的影响

进一步预测R=800 m与R=1 000 m曲线的钢轨滚动接触疲劳损伤，结果如图17所示.由于2条曲线的缓和段长度与R=580 m的不一致，图中均按各自的实际缓和曲线长度绘制.对比图10中R=580 m曲线结果可见，随着曲线半径增大，整条曲线的滚动接触疲劳损伤逐渐减轻，但始终存在出缓和段RCF比入缓和段严重的现象.例如，R=580 m曲线入、出缓和段的疲劳损伤峰值分别为10.0×10-5、12.5×10-5Nf-1，对应纵向疲劳萌生的临界超高为25、14 mm；R=800 m曲线入、出缓和段上，疲劳损伤峰值分别降为5×10-5、6.5×10-5Nf-1，对应临界超高为45、40 mm；R=1 000 m曲线入、出缓和段上，疲劳损伤峰值进一步分别降至2.0×10-5、3.9×10-5Nf-1，对应临界超高为30、28 mm.另外，预测R=800 m曲线入、出缓和段超高72 mm处，外轨疲劳区分别为[-20 , -5]、[-19 , -6]mm，与图4(a)中[-19 , -4]、[-18 , -5]mm吻合；R=1 000 m曲线入、出缓和段超高40 mm处，外轨疲劳区分别为[-21 , -10]、[-21 , -9]mm，同样与图4(b)中[-20 , -11]、[-21 , -10]mm疲劳区对应，再次验证了所建模型的准确性.所研究重载线路上入、出缓和段钢轨RCF差异主要由车轮磨耗廓形主导的结论表明，其他线路上不同的车轮磨耗行为可能会导致与本研究所关注线路不同的结果.换句话说，其他线路不一定发生出缓和段钢轨RCF比入缓和段更严重的现象.

不同半径曲线上入/出缓和段RCF损伤差值如图18所示，其中超高饱和度U（实际超高与圆曲线段超高的比值）分别为30%、60%、90%.可以看出，随着曲线半径增大，入/出缓和段疲劳损伤差值逐渐降低.以超高饱和度90%处为例，损伤差值由R=580 m曲线的5.2×10-5Nf-1，降低至R=800 m曲线的2.6×10-5Nf-1，再至R=1 000 m曲线的1.6×10-6Nf-1.

图18 各半径曲线入/出缓和段不同超高处的外轨疲劳损伤差值对比Fig.18 Rolling contact fatigue differences of high rails for different superelevations for entering/leaving transition section of each radius curve

4 结 语

针对某轴重25 t运煤重载铁路半径580～1 000 m曲线上入/出缓和段钢轨滚动接触疲劳存在差异的现象，建立考虑实测轮轨廓形与轨道不平顺因素的重载列车动力学模型，利用考虑滚动接触疲劳与磨耗竞争机制的损伤函数，分析差异的萌生机理.主要结论如下：1）模型预测的入/出缓和段滚动接触疲劳差异、疲劳区横向位置均与现场观测吻合，验证了本研究所建模型的合理性.2）入/出缓和曲线段钢轨疲劳差异由货车导向轮对的通过行为主导，货车非导向轮对与机车轮对的贡献较小.在标准轮轨廓形匹配下，入/出缓和段钢轨滚动接触疲劳差异不明显，待货车车轮磨耗失形后，作用于出缓和段的轮轨蠕滑率/力高于入缓和段，导致入/出缓和曲线钢轨的滚动接触疲劳差异，钢轨磨耗失形与轨道不平顺入/出缓和曲线钢轨滚动接触疲劳差异的影响不显著.3）随着曲线半径增大，入/出缓和段钢轨滚动接触疲劳的差异逐渐降低，半径1 000 m曲线上缓和段轨面剥离趋于消失，但入/出段差异依然存在.综上所述，上述入/出缓和曲线段钢轨滚动接触疲劳差异是货车车轮失形的结果.本研究针对重载曲线入/出缓和段的钢轨滚动接触疲劳差异现象开展分析，为全面阐释重载铁路曲线段钢轨滚动接触疲劳的萌生机理和治理措施提供了可行的研究与评估手段.未来计划进一步结合实际钢轨打磨与运量情况开展研究.