脆塑性迭代逼近算法的改进
2023-10-08金俊超景来红杨风威宋志宇尚朋阳
金俊超,景来红,杨风威,宋志宇,尚朋阳
(1.黄河勘测规划设计研究院有限公司,河南 郑州 450003;2.水利部黄河流域水治理与水安全重点实验室(筹),河南 郑州 450003;3.中水北方勘测设计研究有限责任公司,天津 300222)
数值算法是有限元计算的关键,对计算结果的准确性和稳定性有直接影响.研究者已在岩石弹塑性及黏弹塑性算法上取得很多成果,如Clausen等[1-4]针对理想弹塑性积分算法中M-C(Mohr-Coulomb)准则和H-B(Hoek-Brown)准则屈服面拐点问题开展研究,Kindrachuk等[5-6]研究了黏弹性和黏塑性积分算法.由于应力-应变关系曲线表现为负斜率,导致刚度矩阵非正定,使得应变软化行为的有限元数值模拟较为困难[7].Sørensen等[8]将应力状态转换为主应力空间,提出基于H-B准则的弹塑性应变软化隐式积分算法,但文献[8]并未给出有限元求解过程的详细说明,考虑到经典塑性力学对软化速率有限制[7],其提出的隐式积分算法可能无法求解峰后软化速率较大的情况.Karavelić等[9]以线性强度准则为例,提出弹塑性应变强化-软化隐式积分算法,但该算法也可能无法求解峰后软化速率较大的情况[7].虽然Jia等[10-17]提出各自的弹塑性损伤模型,并编写UMAT子程序将模型嵌入软件Abaqus,但是当损伤变量为0时,模型退化为弹塑性应变软化模型,所提积分算法也将遇到可能无法求解峰后软化速率较大情况的问题[7].
当岩石强度弱化过程分解为一系列的脆性与塑性交互发生的过程时,软化求解问题可以转化为一系列脆塑性求解问题,规避经典塑性力学求解中对于软化速率的限制[18].Wang等[18]假设应力跌落过程中最小主应力不变,应力从峰值强度跌落至残余强度时Lode参数也不变,提出脆塑性迭代逼近算法及相应的有限元求解过程.虽然脆塑性迭代逼近算法概念明确、方法简单,具有很强的工程应用价值,但是最小主应力不变跌落方法能否正确描述岩石脆塑性变形破坏过程中的应力变化,引入其他应力跌落方法是否必要,都有待进一步分析论证.沈新普等[19]假定应力跌落过程中各应力偏量分量的原有比例保持不变,即应力跌落是从初始屈服面沿着径向向后继屈服面跌落的,提出偏应力等比例跌落方法,并推导弹脆塑性本构积分的数值格式.Zheng等[7]认为跌落时塑性应变增量的方向符合塑性位势理论,提出塑性位势跌落方法,推导给出岩块D-P(Drucker-Prager)准则和结构面M-C准则的塑性跌落因子的计算方法.舒芹等[20]基于带拉伸截断的M-C准则,假设应力跌落过程中应力球量不变,推导破坏粒子应力的计算方法.但是上述最小主应力不变跌落方法、偏应力等比例跌落方法、塑性位势跌落方法等能否正确描述岩石脆塑性应力跌落过程中的应力变化,不同方法各存在什么问题,仍缺少系统性的论证分析.
在脆塑性迭代逼近算法[18]中,采用正确的应力跌落方法是应变软化计算模拟的关键.金俊超等[21]初步分析了不同应力跌落方法的合理性,但理论推导过程中主应力和应力张量概念不清,未分析应力球量不变跌落方法合理性.本研究1)对已有不同方法存在的问题进行系统严谨的论证分析;2)考虑脆塑性变形破坏过程中的泊松效应,改进塑性位势跌落方法,克服已有脆塑性迭代逼近算法中缺陷,在此基础上实现弹塑性变形破坏全过程的模拟;3)通过数值算例验证研究结果的正确性.
1 不同应力跌落方法的问题分析
1.1 已有方法的理论假定与表达式
偏应力等比例跌落方法[19]假设应力由峰值屈服面径向跌落至残余屈服面上,有且仅有各向应力偏量按同一比例β衰减.设峰值强度面应力张量为σp,残余强度系数为β,跌落过程的应力偏量变化量
式中:sp为峰值强度面偏应力张量.跌落后的残余强度面应力张量
最小主应力不变跌落方法[18]针对以压应力为正的情况,假设应力跌落过程中最小主应力不变,应力从峰值强度跌落至残余强度时Lode参数不变.对于以拉应力为正的情况,有
式中:下标1、2、3分别为最大主应力方向、中间应力方向和最小主应力方向;上标p、r分别对应峰值强度面和残余强度面.
Zheng等[7]通过理论推导,证实在脆塑性变形破坏过程中应力的功不负,脆塑性材料仍满足Il’yushin公设.在此基础上,假定跌落过程产生的塑性应变增量Δεp的方向满足塑性位势理论:
式中:Δa为塑性流动因子;考虑到通常采用剪胀角来衡量岩体的剪胀变形,采用M-C准则型式塑性势函数.假定脆塑性应力跌落过程中总应变保持不变,则弹性应变的增加等于负的塑性应变,以主应变形式表示为
根据式(5)计算跌落过程中的应力增量Δσ,以主应力、主应变形式表示为
式中:λ为Lamé参数,G为切变模量.
应力球量不变跌落方法[20]假设应力由峰值屈服面径向跌落至残余屈服面上,应力跌落前后的应力圆半径发生变化,圆心保持不变,且应力跌落过程中应力主轴不旋转,对于以拉应力为正的情况,有
1.2 不同方法存在的问题分析
如图1所示,岩石的变形破坏分为单轴拉伸破坏、拉剪破坏、纯剪破坏及压剪破坏.由于直接从三维应力空间对已有应力跌落方法存在的问题进行理论推导分析较为困难,本研究以经典的线性M-C准则为例,从单轴拉伸破坏、单轴压缩破坏及二向纯剪破坏特征点,分析现有方法的模拟正确性.如果单轴压缩破坏、单轴拉伸破坏及二向纯剪破坏不能正确计算,那么拉剪、压剪等复合破坏类型也无法正确计算.从主应力空间推导不同方法的脆塑性应力跌落计算过程,理论公式如表1~4所示.可以发现,已有脆塑性应力跌落方法,虽然能描述某种脆塑性变形破坏过程,但无法正确模拟全部破坏方式.在实际工程中,围岩变形破坏往往多种破坏方式并存,已有方法无法适用于不同破坏方式的计算,阻碍了计算模拟的正确性.

表2 最小主应力不变跌落方法存在的问题Tab.2 Defects of existing calculation method based on constant minor principal stress in brittle-plastic process

表3 塑性位势跌落方法存在的问题Tab.3 Defect of existing calculation method based on plastic potential theory

表4 球量不变跌落方法存在的问题Tab.4 Defect of existing calculation method based on invariant spherical stress

图1 岩石破坏分类Fig.1 Schematic of rock failure types
2 塑性位势跌落方法的改进及验证
偏应力等比例跌落方法[19]、最小主应力不变跌落方法[18]及应力球量不变跌落方法[20]均采用人为假定应力跌落路径.塑性位势跌落方法[7]满足弹塑性理论中的Il’yushin公设,无需人为假定应力跌落路径,理论更为严谨,本研究将针对塑性位势跌落方法存在的不足,考虑泊松效应进行方法改进.
2.1 脆塑性变形破坏过程中的泊松效应分析说明
原有塑性位势跌落方法[7]假设脆塑性变形破坏过程中总应变保持不变,这与如图2所示的试验结果一致.Zheng等[7]未考虑泊松效应,简单认为弹性应变的增加等于负的塑性应变,由此得到式(6).事实上,岩石作为弹塑性材料,存在泊松效应.以主应力、主应变型式进行说明,在脆塑性变形破坏过程中,某个主方向发生弹性变形(等于负的塑性应变)由于泊松效应,必然在其他2个正交主方向产生横向弹性应变,对应的回弹应变增量

图2 红砂岩单轴拉伸试验结果[22]Fig.2 Uniaxial tension test of red sandstone[22]
因此,脆塑性变形破坏过程中的弹性应变增量Δεe应为该方向上负的塑性变形Δεp和泊松效应引起的回弹应变增量Δεde的叠加:
式(6)与式(9)存在显著差异,证明考虑脆塑性变形破坏过程中的泊松效应后,弹性应变增量计算公式发生变化,应力增量计算公式也相应改变:
在岩石弹塑性变形破坏过程中泊松比存在一定变化,为了简化,本研究以泊松比v为定值进行理论推导,对于考虑泊松比变化的情况,理论推导过程一样,只要将v考虑为非定值.
如表5所示,考虑脆塑性变形破坏过程中的泊松效应,分别针对单轴拉伸破坏、单轴压缩破坏和二向纯剪破坏等破坏类型进行计算理论推导.可以发现,此时塑性位势跌落方法可以正确计算多种情况下的岩石脆塑性变形破坏过程.
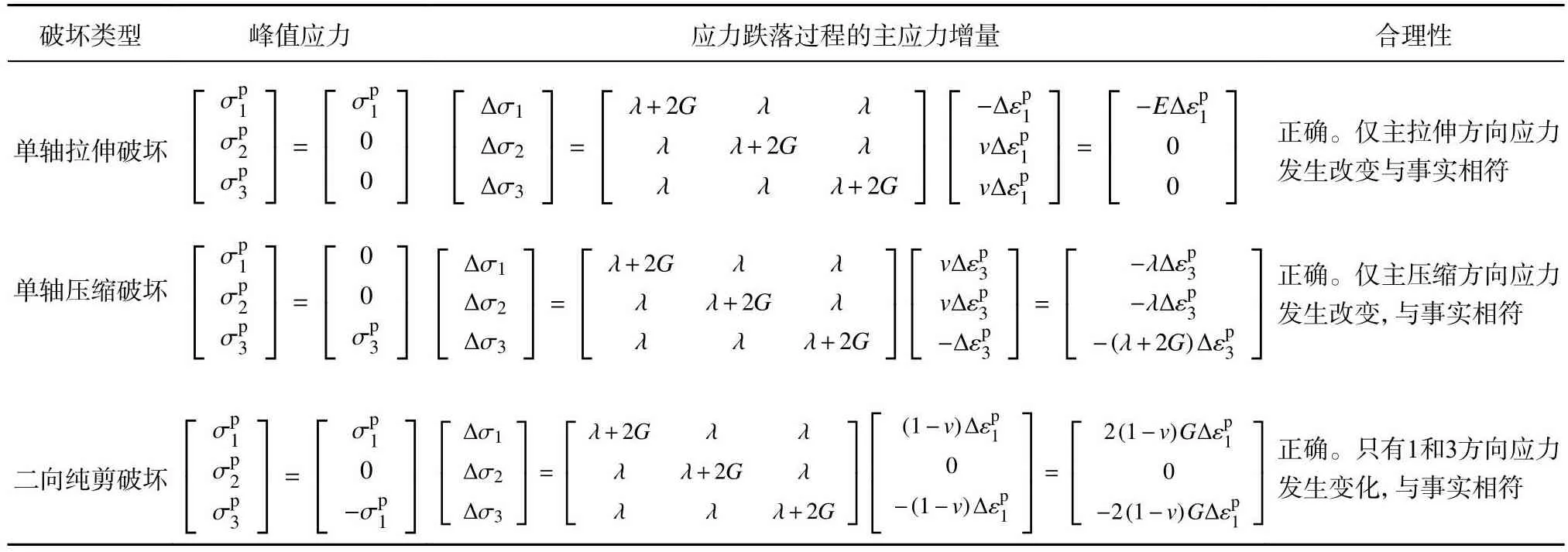
表5 基于泊松效应的改进塑性位势跌落方法的合理性Tab.5 Rationality of improved calculation method based on plastic potential theory considering Poisson’s effect
2.2 塑性位势跌落方法的改进
在三维应力空间考虑脆塑性变形破坏过程中的泊松效应,对原有塑性位势跌落方法进行改进.塑性应变增量Δεp、回弹应变增量Δεde及弹性应变增量Δεe的计算公式分别为
跌落过程应力增量
式中:D为弹性刚度矩阵,由弹性模量E和泊松比v构成.残余应力
式中:n+1、n表示第n+1和第n次迭代;p1、p3为以主应力表示的迭代过程应力增量.设Δa0=0,当不超过预设精度时,跳出迭代;将Δan+1代入式(11),计算得到脆塑性应力跌落过程的塑性应变增量Δεp;根据式(12),计算得到回弹应变增量Δεde;根据式(13),计算得到弹性应变增量Δεe;根据式(14)、(15),计算得到跌落过程应力增量Δσ及最终残余应力σr.根据上述计算步骤编制UMAT子程序,将改进塑性位势跌落方法嵌入软件Abaqus,实现脆塑性变形破坏问题的有限元求解.
2.3 室内试验模拟验证
2.3.1 红砂岩单轴拉伸试验模拟验证 根据红砂岩试验资料[22],构建标准圆柱体有限元模型,试件直径为50 mm,高为100 mm.在模型底部设置法向链杆约束,顶部施加位移荷载,进行单轴拉伸试验模拟.如图3所示为本研究所提方法模拟结果与试验结果的对比.可以看到,虽然由于将峰前简化为线弹性,导致模拟结果与试验结果存在一定差异,但整体上,本研究所提方法可以正确模拟红砂岩单轴拉伸脆塑性变形破坏过程,模拟的残余阶段轴向及横向应力均为0(点B、B'),与试验结果一致.将原有塑性位势跌落方法模拟的跌落后应力点绘于图中(点C、C' ).对于脆塑性变形破坏过程,在峰值及残余强度参数给定的情况下,不同脆塑性应力跌落方法的模拟结果主要的差异是跌落后的应力模拟结果,因此本研究将分析重点放在跌落后的应力模拟结果正确性上.原方法计算的跌落后轴向拉应力为-0.03 MPa,横向应力变为-0.20 MPa,与试验结果不符,证明原有塑性位势跌落方法不能正确模拟岩石单轴拉伸脆塑性变形破坏过程.

图3 红砂岩单轴拉伸应力-应变模拟曲线对比Fig.3 Comparison of simulated stress-strain curves of red sandstone under uniaxial tension
2.3.2 花岗岩三轴压缩试验模拟验证 根据花岗岩试验资料[23],构建标准圆柱体有限元模型,在模型底部设置法向链杆约束.在顶部及环向施加静水压力至额定围压,再在顶部施加位移荷载,进行三轴压缩试验模拟.如图4所示为本研究所提方法模拟结果与试验结果的对比.由于残余强度参数拟合值与试验结果的误差,导致本研究模拟的残余强度点与试验结果存在差异(点B1-B3和B′1-B′3).如表6所示为提取残余强度模拟结果与试验数据拟合值.由表可知,模拟的残余阶段轴向应力与拟合结果一致,模拟的横向应力始终与围压保持一致,证明本研究所提方法能够正确模拟岩石三轴压缩脆塑性变形破坏过程.将原有塑性位势跌落方法计算的跌落后应力绘于图中(点C1-C3、C1′-C3′),相应数据见表6,原方法在不同围压的跌落后应力模拟结果,均与试验数据拟合值存在很大差异,证明原有塑性位势跌落方法不能正确模拟岩石三轴压缩脆塑性变形破坏过程.

表6 2种应力跌落计算方法的残余应力模拟结果对比Tab.6 Simulated residual stress of two stress-drop calculation method MPa

图4 花岗岩三轴压缩应力-应变模拟曲线对比Fig.4 Comparison of simulated stress-strain curves of granite under triaxial compression
2.3.3 砂岩压剪试验模拟验证 根据砂岩压剪试验资料[24],构建40 mm×40 mm×40 mm的立方体试件.试件的底面采用法向链杆约束,顶面施加压应力1.5 MPa;再在试件上部施加法向链杆约束,试件下部施加水平位移荷载,进行压剪试验模拟.如图5所示为改进方法与原有塑性位势跌落方法的应力-应变模拟曲线对比,点A、A′为峰值和残余剪应力试验点,点B为本研究所提方法模拟的残余应力点,点C为原方法模拟的残余应力点.可以看到,本研究所提方法模拟的残余阶段剪应力与试验结果一致,证明本研究所提方法可以正确模拟砂岩压剪脆塑性变形破坏过程;原有方法模拟的残余剪应力与试验值相差33.5%,验证了原方法不能正确模拟砂岩压剪脆塑性变形破坏过程.其中σn为法向压应力.

图5 砂岩压剪应力-应变模拟曲线对比Fig.5 Comparison of simulated stress-strain curves of sandstone under compression and shear
单轴拉伸试验、三轴压缩试验及压剪试验模拟涵盖主要的变形破坏类型,充分证实了改进塑性位势跌落方法能够正确模拟多种情况下的岩石脆塑性变形破坏过程;原方法存在缺陷,无法正确模拟多种情况下的岩石脆塑性变形破坏过程.
3 脆塑性迭代逼近法的改进及验证
3.1 脆塑性迭代逼近法的改进
脆塑性迭代逼近法的核心是脆塑性应力跌落过程的模拟[18].塑性强化及理想塑性积分算法研究较为成熟,Clausen等[1-4,21]通过建立强度参数随塑性应变的演化方程,在向后欧拉隐式积分算法的基础上引入塑性硬化参与迭代计算,使得屈服面在迭代过程中与应力一同更新(屈服面的大小会随着塑性损伤的更新而变化)直至应力回到屈服面上.本研究将对如何在所提改进塑性位势跌落方法基础上实现应变强化-软化数值模拟展开说明.
如图6所示,将改进塑性位势跌落方法与理想塑性流动算法结合,通过多级脆塑性跌落-塑性流动,实现弹塑性应变软化的数值模拟,克服已有脆塑性迭代逼近算法[18]中应力跌落方法不正确的缺陷.将改进的弹塑性应变软化算法与塑性强化算法结合,实现岩石塑性强化-峰后软化-残余强度的变形破坏全过程模拟.通过编译UMAT子程序,将计算过程在软件Abaqus中实现,其中塑性强化和理想塑性流动过程采用向后欧拉隐式积分算法,具体参见文献[21].

图6 岩石弹塑性变形破坏全过程计算流程Fig.6 Numerical procedures of full elasto-plastic deformation and failure process
3.2 算例验证
已有脆塑性应力跌落方法均存在不足,以此为基础建立的脆塑性迭代逼近算法也存在缺陷;所提改进塑性位势跌落方法具备正确性,以此为基础建立的脆塑性迭代逼近算法具备正确性.本研究将通过室内三轴压缩试验和应变软化圆隧围岩力学响应规律模拟,检验所提方法的正确性,不再与原方法的模拟结果进行对比.
1.3.3 潜在生态危害指数法。瑞典科学家Hakanson[10]提出的生态危害指数法是目前最为流行的一种对土壤或沉积物中土壤重金属污染进行评价的方法。该法将重金属的生态效应、环境效应与毒理学联系在一起,不仅反映了某一特定环境中各种污染物对环境的影响,及多种污染物的综合效应,而且用定量的方法划分出了潜在生态风险的程度。其计算公式为:
3.2.1 室内三轴压缩试验模拟验证 韩建新等[25]基于M-C准则,假设黏聚力和内摩擦角为最大主应变的分段线性函数,提出岩石应变软化模型,并模拟Tennessee大理岩三轴压缩试验;沈华章等[26]分别假定峰前和峰后阶段强度参数随软化参数按照指数函数演化,塑性变形遵守非关联流动法则,对三峡花岗岩的三轴压缩试验进行数值模拟.如图7所示为Tennessee大理岩及三峡花岗岩三轴压缩试验结果和模拟结果的对比.可以看到,模拟结果与试验数据具有良好的可比性,实现了Tennessee大理岩峰后塑性软化-残余强度变形破坏全过程的正确计算,也实现了三峡花岗岩塑性强化-峰后脆性跌落-塑性软化-残余强度变形破坏全过程的正确计算.对比结果验证了所提弹塑性变形破坏全过程数值算法的正确性.

图7 Tennessee大理岩及三峡花岗岩的三轴压缩试验模拟Fig.7 Experimental simulation of triaxial compression for Tennessee marble and Sanxia granite
3.2.2 应变软化圆隧围岩力学响应规律模拟 如图8所示,假定强度参数和剪胀角随塑性剪应变分段线性演化规律,Lee等[27]将潜在塑性区围岩按等围压释放划分为若干同心圆,采用塑性区按相等的应力增量划分、围压逐渐递减的差分方法,给出了应变软化圆隧围岩力学响应规律解析解;Park[28]用一阶常微分方程代替应力平衡、本构关系和一致性条件的偏微分方程,采用Runge-Kutta求解常微分方程,给出圆隧围岩力学响应规律解析解.如图9所示为圆隧收敛位移及应力分布解析解和本研究有限元模拟结果对比.可以看到,本研究所提方法计算的围岩特征曲线与Lee等[27]和Park[28]的解析解十分接近,所提方法计算的支护应力pi=0时的围岩径向及切向应力分布与Park[28]的解析解也具有较好的可比性,证明所述的数值实现工作在整体模型层次正确有效.
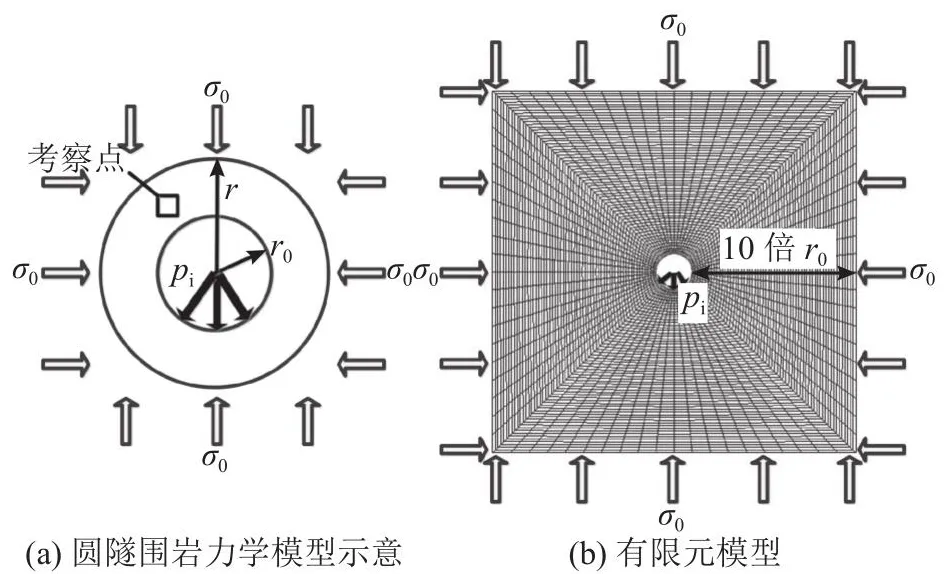
图8 圆隧围岩挖掘及有限元模型Fig.8 Example of circular tunnel excavation and FEM

图9 圆隧力学响应有限元模拟结果与解析解对比Fig.9 Comparisons of numerical and theoretical results of circular tunnel excavation
4 工程算例
4.1 Mine-by试验洞破坏区模拟
Mine-by试验圆洞长46 m,直径3.5 m,埋深420 m,围岩为Lac du Bonnet花岗岩.试验洞采用非爆破的机械开挖方法,开挖过程中围岩不断发生脆性剥落破坏,形成典型的V形脆性破坏区[29].由于监测资料完整,已被包括Hajiabdolmajid等[29-30]在内的多位学者用以验证所建力学模型的合理性.本研究将利用所提有限元计算程序引用已有本构模型和参数,对试验洞进行开挖模拟,并与监测结果对比,验证所提方法的正确性.Mine-by隧洞的有限元模型如图10所示,水平方向和竖直方向各取17.5 m,沿隧洞轴线方向取1 m;共划分单元18 732个,开挖面附近单元宽度为0.1 m,厚度方向划分3层网格;在模型底部及四周表面采用法向约束;围岩计算参数如表7所示.
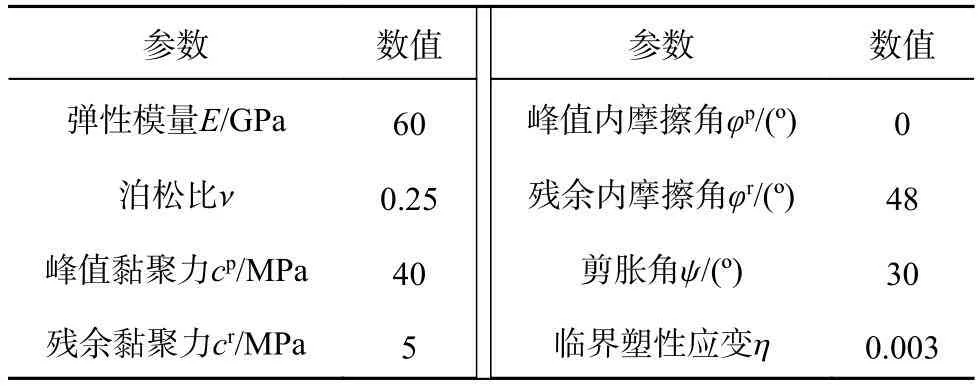
表7 Mine-by隧洞围岩计算参数Tab.7 Model parameters of surrounding rock of Mine-by tunnel

图10 Mine-by隧洞有限元模型Fig.10 Numerical model of Mine-by tunnel
如图11所示,图中εep为等效塑性应变,c为黏聚力.开挖导致高地应力集中在巷道顶部和底板,这些部位的强度参数变化最为明显.模拟的顶拱塑性区最大深度为2.56 m,如图12(a)所示,微震数据确定的最大深度为2.57 m,数值与分布区域基本一致.模拟的顶拱破坏区最大深度为2.27 m,如图12(b)所示,接近实测的破坏区最大深度2.3 m,形状与实测情况基本吻合.
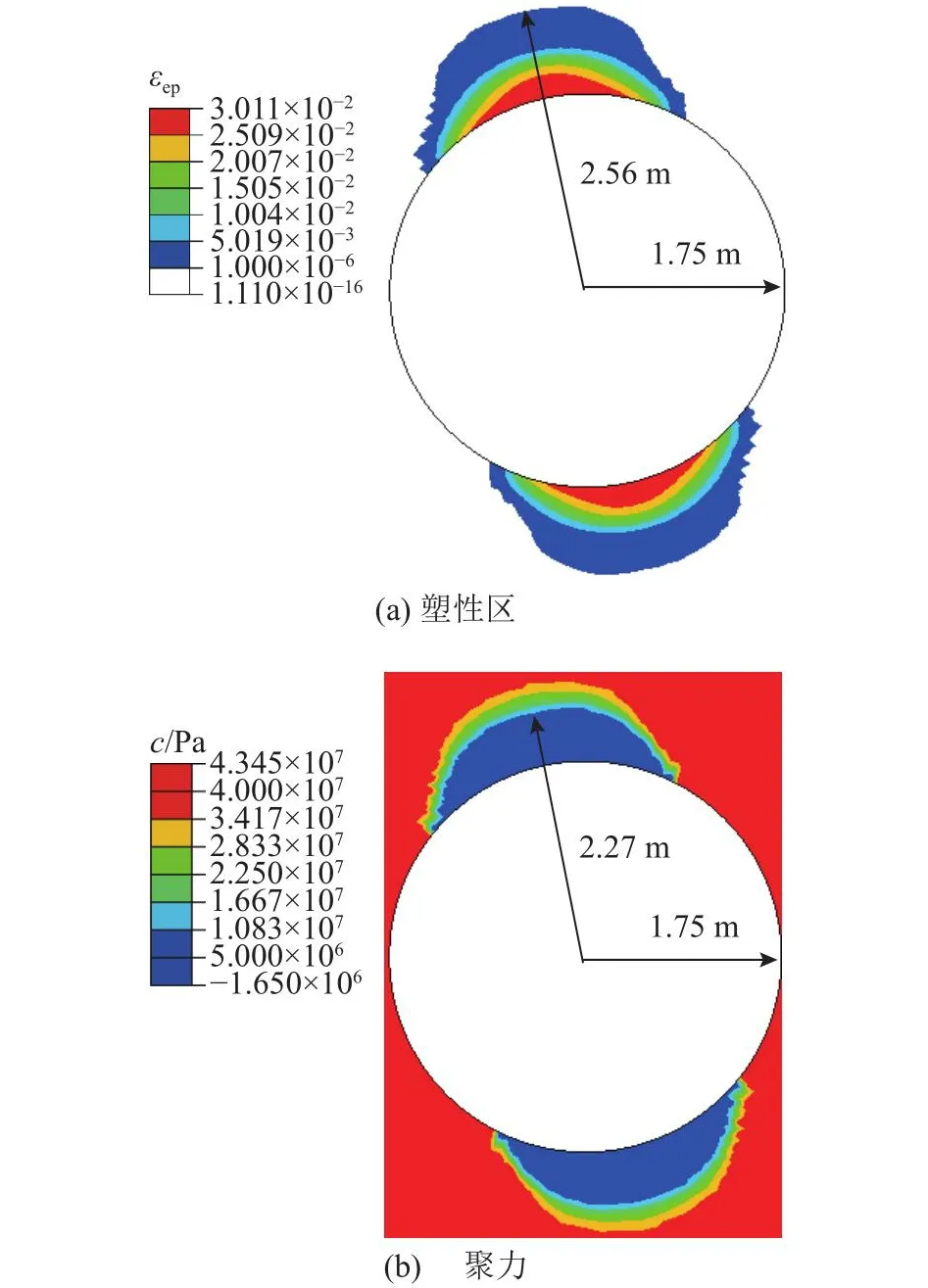
图11 模拟的隧洞塑性区和破坏区Fig.11 Simulated plastic and failure zones by proposed method

图12 监测的隧洞塑性区和破坏区[29]Fig.12 Monitored plastic and failure zones[29]
4.2 某水电站引水隧洞辅助洞松动圈模拟
为了了解围岩在开挖扰动下的损伤区范围,在某水电站引水隧洞辅助洞A和辅助洞B的多个断面进行声波测试.以辅助洞A中的AK10+900断面为研究对象,根据声波测试结果确定的开挖松动圈[31]如图13所示,通过本研究所提应变软化有限元计算程序模拟开挖塑性区,检验本研究所提方法的正确性.辅助洞的有限元模型如图14所示,水平方向和竖直方向各取70 m,隧洞轴向取3 m;共划分单元55 170个,开挖面附近单元宽度为0.2 m;模型底部及四周表面采用法向约束.初始地应力场为σx=-48.98 MPa,σy=-55.67 MPa,σz=-66.16 MPa,τxy=-2.52 MPa,τyz=-0.30 MPa,τxz=7.17 MPa[31].参考已有研究及室内试验结果[31-32],综合确定围岩计算参数如表8所示.

表8 辅助洞围岩计算参数Tab.8 Model parameters of surrounding rock of auxiliary tunnel

图13 AK10+900断面开挖松动圈[31]Fig.13 Plastic zone at section AK10+900[31]

图14 辅助洞有限元模型Fig.14 Numerical model of auxiliary tunnel
如图15所示,开挖导致高地应力集中在两侧边墙及拱角位置,这些部位的强度参数变化最为明显.本研究所提方法模拟的松弛深度平均值为1.35 m,现场试验监测平均值为1.66 m,相差0.31 m.与已有模型相比,文献[31]模拟的测线塑性区深度与监测结果的总方差为8.30,文献[32]模拟的总方差为10.96,本研究所提方法模拟的为7.11,较已有研究分别减小了16.59%和32.13%.对比结果表明,本研究所提方法能够较为合理地描述辅助洞围岩的弹塑性变形破坏现象.
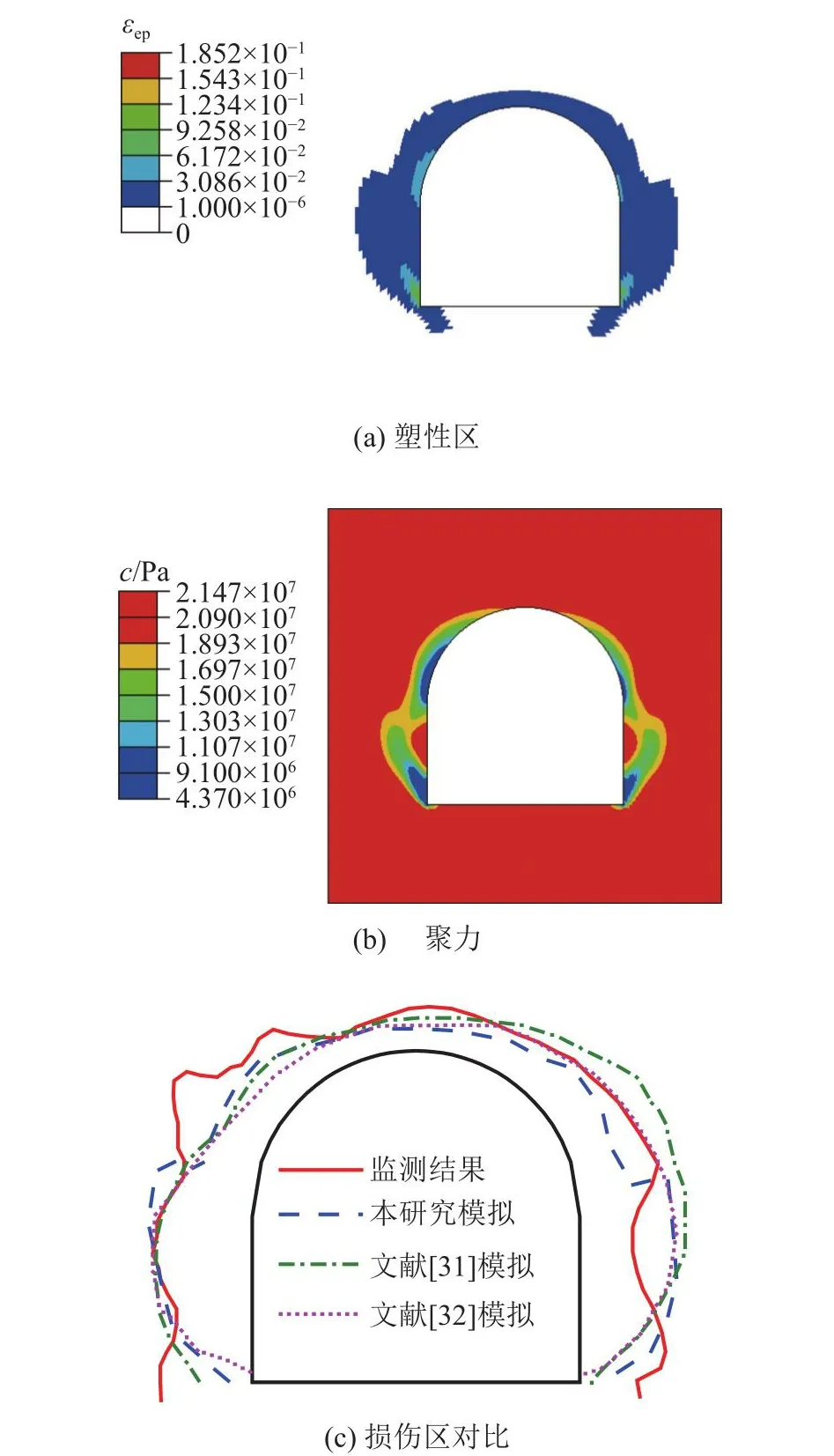
图15 开挖模拟结果Fig.15 Simulated results by proposed method
5 结 论
(1)在主应力空间,结合特征点变形破坏特征,论证偏应力等比例跌落方法、最小主应力不变跌落方法及塑性位势跌落方法均存在不足:不能正确模拟多种情况下岩石脆塑性变形破坏过程.
(2)考虑脆塑性变形破坏过程中的泊松效应,提出改进塑性位势跌落方法,推导具体应力更新过程,并嵌入软件Abaqus.
(3)岩石室内多种类型破坏试验模拟结果证实:改进塑性位势跌落方法能够正确模拟多种情况下的岩石脆塑性变形破坏过程.改进塑性位势跌落方法克服了原有塑性位势跌落方法的缺陷,为脆塑性迭代逼近算法的改进奠定了基础.
(4)采用所提改进塑性位势跌落方法替换原有脆塑性迭代逼近算法中的应力跌落计算方法,能够实现弹塑性应变软化过程的数值模拟.引入塑性强化算法,实现了弹塑性变形破坏全过程的正确计算.
(5)不同地质条件的Mine-by试验洞和某水电站引水隧洞辅助洞开挖模拟结果与现场监测结果均吻合良好,证明本研究所提方法能够合理模拟工程中围岩弹塑性变形破坏现象.
(6)本研究基于线性M-C准则,提出了改进塑性位势迭代逼近算法,实现了弹塑性应变软化过程的数值求解.非线性Hoek-Brown准则、岩石弹塑性损伤变形破坏过程,有待在本研究基础上深入拓展.
