电路等效变换的性质及其应用

田社平 张 峰

(上海交通大学 电子信息与电气工程学院, 上海 200240)

电路的等效变换和等效电路是电路理论中重要的概念。所谓等效电路,是指如果端子一一对应的n端电路N1和N2具有相同的VCR,即相同的两组端电压分别代入两个电路的端口VCR会得出相同的两组端电流,或者将相同的两组端电流代入两个电路的端口VCR会得出相同的两组端电压,则两者互称等效电路。从一个电路变换为与之等效的另外一个电路的过程则称为等效变换。利用等效变换和等效电路的概念,可以极大地简化电路的分析。在电路理论教学中,为讲授、证明诸如电阻的串联和并联、T形电路和Π形电路、戴维南电路和诺顿电路等之间的等效关系,现行教材大多基于等效电路的定义,亦即,如果所求得的两个电路的端口VCR相同,则这两个电路就是等效的[1-4]。显然,这样的讲授、证明方法无疑是正确的、合理的,也是基本的。这只是问题的一个方面,采用定义来证明电路的等效性有时显得较为繁复,证明过程中涉及较为复杂的运算,从而增加了学生理解的负担。因此,有必要探讨更为简洁、容易理解的证明两个电路等效的讲授方法。

任何一个对象,赋予其定义后,它一定具有相应的性质。基于此,本文从等效电路的定义出发,总结出等效电路所具有的性质,并利用该性质证明电路的等效性,或者进行电路的分析,结果发现,证明或分析的过程得到了简化。

1 电路等效变换的性质

关于等效电路,我们可以得到如下两个性质:

【性质1】如果两个电路等效,在两个电路的某些端钮(或端口)连接相同的任意电路,则得到的两个新电路也是相互等效的。

这里,“等效”的含义仍然是针对电路端口而言的。

【性质2】对两个电路,如果在两个电路的某些端钮(或端口)连接相同的任意电路,所得到的两个新电路是相互等效的,则这两个电路相互等效。

上述性质是两个互逆的命题。性质1是显而易见的。这是因为,如果两个电路等效,则其端口VCR是相同的;在这两个电路的某些端钮(或端口)连接相同的任意电路,所增加的端口约束方程也是相同的(因为连接的电路是相同的),这样就得到了两组完全相同的方程组,其解也必然相同。注意,这里默认两组方程都只有唯一解。

性质2的证明可采用反证法。假设这两个电路不是等效的,则两个电路的端口VCR方程不是完全相同的。由于在两个电路的某些端钮(或端口)连接的是相同的任意电路,它们的端口VCR又是相同的,因此就得到了两组不完全相同的方程组。在这种情况下,总归可以找到这样的外接电路(因为是任意电路,所以外接电路是可以选择的),使得两组不完全相同的方程组的解不同,这与性质2所给条件相矛盾。因此性质2是成立的。

上述两个性质是等价的,它们在分析有关电路等效变换的问题中能得到很好的应用。

2 应用

【例1】戴维南电路和诺顿电路的等效变换。如图1(a)、图1(b)所示分别为戴维南电路和诺顿电路,其中的R为电阻,G为电导。在假设图1两个电路可以相互等效的前提下,为求出两者等效变换的关系式,一般教材都通过列写两者的端口VCR方程,比较两个方程的一致性得到结果。尽管其推导过程是比较简单的,但是利用上述性质,同样可以非常方便地得到相同的结论。

(a) 维南电路

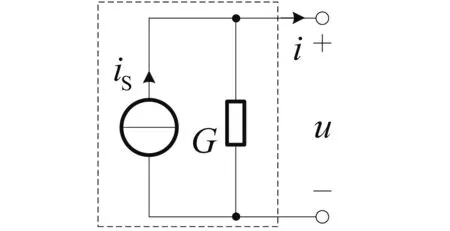
(b)诺顿电路图1 戴维南电路和诺顿电路的等效

图1两个电路都包含两个元件参数,因此只须在两个电路的端口接入两种相同的电路即可。为分析方便,可选择开路和短路这两种电路分别接入。图1两个电路的端口开路时,其开路电压相同,即得

uS=iS/G

(1)

图1两个电路的端口短路时,其短路电流相同,即得

uS/R=iS

(2)

整理式(1)、式(2),得到等效关系式

(3)

可以看出,上述推导过程非常简单。

【例2】T形电路和Π形电路是可以相互等效的,其等效变换是电路理论教学中的重点,如果基于等效电路的定义推导其等效关系,则推导过程较为复杂,而利用等效变换的性质进行推导则非常简洁。部分国内外教材就采用了基于上述性质的推导方法[5-7]。下面给出略异但推导过程更简单的方法。

按照性质1,我们可以在T形电路和Π形电路某一端口外接合适的电路,而在另外的端口观察其端口特性。

端钮间(或端口)外接电路最简单的情况就是开路和短路。将图2中两个电路的2端分别开路,则从1、3端看进去的等效电阻应相等,即

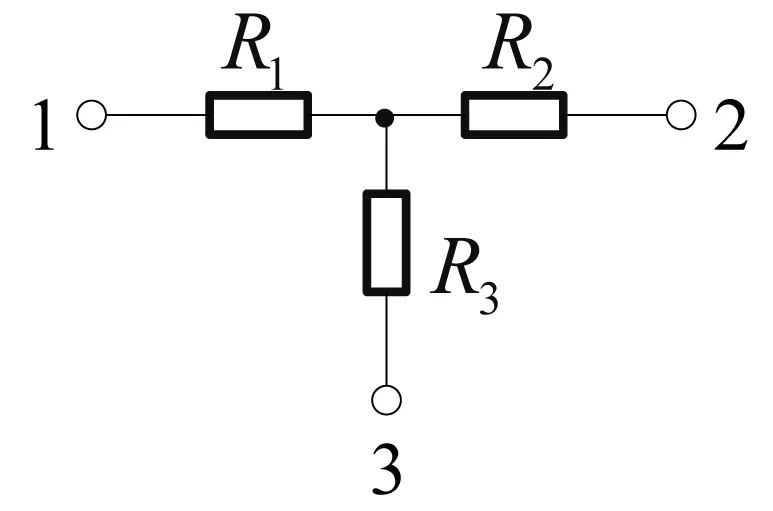
(a) T形电路

(b)Π形电路图2 T形电路和Π形电路的等效

(4)

类似地,可以得到

(5)

(6)

式(4)～式(6)是关于R1、R2、R3的线性方程组,不难解得R1、R2、R3的表达式,从而得出Π形电路等效变换为T形电路的公式为

(7)

或

(8)

将图2中两个电路的1、3端分别短接,则从短接端、2端看进去的等效电导应相等,即

(9)

类似地,可以得到

(10)

(11)

同样,式(9)～式(11)是关于G12、G23、G31的线性方程组,类似地,不难得出T形电路等效变换为Π形电路的公式为

(12)

或

(13)

由上述分析过程可以看出,整个推导过程并不复杂,而且方程求解仅涉及线性方程,也非常简单。相比较而言,现行教材基于等效的定义,推导时须求出T形电路和Π形电路的端口VCR方程,而且在比较两个VCR方程时还涉及矩阵的逆运算,其过程较为复杂。

【例3】如图3(a)所示耦合电感为全耦合电感。如果图3(b)电路与图3(a)电路等效,那么参数Le、n应满足什么关系?

(a) 全耦合电感

(b)等效电路图3 全耦合电感等效电路

为便于比较,首先基于等效电路的定义来求解。图3(a)电路的端口VCR满足

(14)

为求图3(b)电路的端口VCR,列写图3(b)电路输入端口的KVL方程,得

(15)

(16)

又由理想变压器特性可得

(17)

比较式(14)与式(16)、式(17),可得出参数Le、n应满足的关系为

(18)

下面利用等效变换的性质来求解。按照性质1,我们可以在图3两个电路的对应端口外接合适的电路,而在另外对应的端口观察端口特性。将图3两个电路的输入、输出端口开路,则从两个电路的输入端看进去的等效电感分别为L1、Le;从两个电路的输出端看进去的等效电感分别为L2、Le/n2。由于两个电路等效,因此有

(19)

此即式(18)。整个推导过程显得非常简单。

值得注意的是,上述推导过程并没有用到“全耦合”这一条件!这表明,两个电路外接“非任意”的相同电路是等效的,仅仅是这两个电路等效的必要条件,而非充分条件。但这并不妨碍等效变换性质的应用。一方面,题目所给条件说明只有图3(a)电路是全耦合情况时才有可能与图3(b)电路等效,亦即图3两个电路是可以相互等效的。另一方面,只有式(19)成立,图3(b)电路才能与图3(a)电路等效。从分析问题的角度,上述推导是合理的。

当然,如果选择另外的外接电路,也可推出相同的结果。比如,将图3两个电路的输出端口开路,则从两个电路的输入端看进去的等效电感分别为L1、Le;将图3两个电路的输入端口外接电感L1,则从两个电路的输出端看进去的等效电感分别为L2/2、(L1//Le)/n2。由于两个电路等效,因此有

(20)

整理上式,同样得到式(18)。整个推导过程也不复杂。

【例4】耦合电感的T形去耦等效电路。如图4(a)所示,当耦合电感互相联结于一个公共端子时,可用三个相互间无互感的电感组成的T形电路等效,如图4(b)所示。为推导两个电路的元件参数间,可保持三端之一端为开路,比较另外两端看进去的等效电感。图4(a)电路从12端、23端、31端的等效电感分别为:L1+L2-2M、L2、L1;对图4(b)电路,则分别为LA+LC、LB+LC、LA+LB。由此可得

(a) 耦合电感

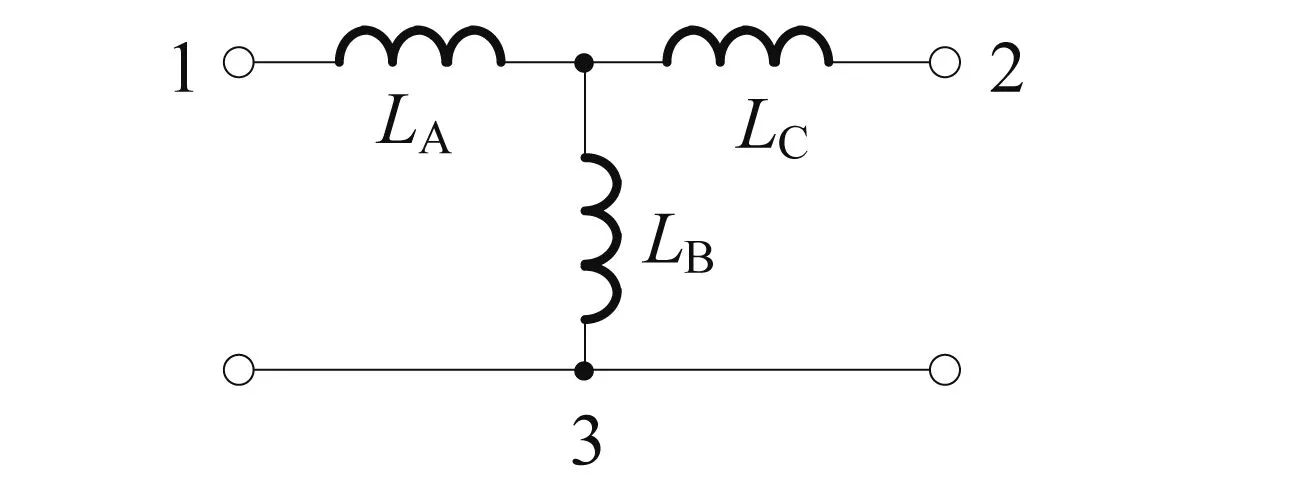
(b)T形去耦等效电路图4 耦合电感的T形去耦等效电路

(21)

由上式解得

(22)

可见,推导过程十分简明。

利用等效变换的性质推导耦合电感的Π形去耦等效电路的关系式也是非常简单的,不再赘述。

3 结语

本文讨论了等效电路的性质及其应用,该性质非常直观,也易于理解。所举例子表明,利用该性质能够极大简化有关等效电路问题的分析。笔者曾尝试利用上述性质讲解电路等效变换的相关知识点,如T形电路和Π形电路的等效变换、耦合电感的去耦等效电路,取得了较好的效果。