冲积河流平滩流量的确定方法研究

2023-10-07孙赞盈范冰洁尚红霞

人民黄河 2023年10期

孙赞盈，范冰洁，张敏，尚红霞

（1.黄河水利科学研究院，河南郑州 450003；2.山西黄河机动抢险队，山西运城 044000）

黄河下游防洪因悬河形势而变得十分特殊和异常重要。受黄河干流来沙量减少和小浪底水库蓄水拦沙的影响，2000 年以来，黄河下游河道绝大部分时间处于冲刷状态，截至2021 年汛末，与小浪底水库运用前的1999 年相比，7 个水文站的3 000 m3/s 同流量水位降幅在1.54～3.44 m 之间，高村站及其以上河段的水位降幅明显，在2.66～3.44 m 之间，降幅最大的夹河滩站为3.44 m，孙口和利津站降幅较小，其中利津站最小，为1.54 m。尽管如此，黄河下游的悬河形势依然没有显著减轻，以黄河下游卡口河段的孙口站为例，2021年汛后，其流量3 000、4 000 m3/s 和最大流量5 050 m3/s 对应水位分别为44.98、45.65、46.48 m，分别比右岸的堤根高程高2.74、3.41、4.24 m。可见，还需要持续冲刷以降低黄河下游河槽高程。大量已有研究成果显示，在其他条件不变的情况下，水流的流量越大，则流速越大，冲刷效率越高［1－3］。但另一方面，若流量过大引起漫滩，不但会造成黄河下游滩区淹没，带来不必要的损失，而且漫滩后因滩槽水流动量交换，还会使水流流速降低［4－5］，冲刷效果变差。因此，小浪底水库调节出库流量过程，以卡口河段平滩流量为控制流量泄放，将会取得治河和不影响滩区生产生活“双赢”的效果，这就要求准确确定黄河下游平滩流量。黄河下游河道长达850 km，加上冲淤和河势变化，准确确定平滩流量并不是一件容易的事情。

黄河水利委员会每年要在汛前准备好《黄河中下游防御大洪水方案》，而黄河下游防洪是其中的关键内容，这就要求更早提出黄河下游的平滩流量成果，时间上非常紧迫。因此，提出一个结果可靠、使用简单的平滩流量确定方法，是十分必要的。

平滩流量是冲积河流河床演变研究的一个重要指标，涉及平滩流量的文献众多。这些文献可分为两类：其一是研究平滩流量与影响因素的关系，不涉及如何确定平滩流量，这类研究比较多，如文献［6－16］；其二是确定平滩流量的方法，如文献［17－19］。在确定平滩流量的方法中，有人把延长水位流量关系得到平滩流量作为一种方法，且仅限于有实测水位和流量的水文站，陈述比较简单，没有涉及利用险工水尺的水位资料确定大断面平滩流量。

1 已有方法存在的问题

以往在确定平滩流量时，多采用根据曼宁公式计算的办法。曼宁公式实际上有一个简单的前提条件：断面必须是矩形或接近矩形。通常曼宁公式适用于诸如渠道这样的边界条件非常简单的情况。曼宁公式应用于冲积河流的天然河道时，至少存在如下4 个方面问题。

1.1 平面上（水面宽）沿程变化的问题

冲积河流很少有沿程断面形态规则的情况，受各种因素影响，其水面沿程总是宽窄相间的。图1 为2019 年汛期最高洪水位期间黄河下游宽河道淤积断面水面宽沿程变化（相应8 月7 日花园口站洪峰流量5 050 m3/s），可以看出，水面宽沿程变幅很大，最窄的断面水面宽不到300 m，最宽的达2 475 m；河道宽窄相间，有的河段水面宽从数百米突然展宽到上千米，然后又收缩至数百米。当水流从窄断面过渡到宽断面再过渡到窄断面时，宽断面的岸边会形成旋涡（见图2），水流就地旋转，这部分水流并不是有效的过流，若采用曼宁公式计算，必然将其作为过流对待，显然不合理。

图1 2019 年汛期最高洪水位期间水面宽沿程变化

图2 宽窄相间的断面产生旋涡示意

1.2 垂向上（河床高程）沿程变化的问题

大量的黄河实测大断面资料显示，在河道纵向上，地形起伏变化很大。图3 为2019 年汛前实测大断面的最低点高程和实测洪水位沿程变化。可以看到，在纵向上，断面的最低点高程沿程变化幅度极大，相邻断面的最低点高程相差10 m 的情况屡见不鲜，而洪水位反映的水面线是光滑的，并无上下起伏现象。

图3 最低点高程和实测洪水位沿程变化

如果一个断面的上、下断面高程较高，那么水流会在该断面的底部产生旋涡（见图4），也就是说，并不是整个断面都是输送水流的，采用曼宁公式计算就会将过流量计算得很大，这显然与实际不符。

图4 较深的断面底部产生旋涡示意

1.3 动床影响的问题

通过对黄河干支流不同比降（0.050‰～0.635‰）的河段、不同含沙量（21.7～923 kg/m3）和不同流量（1 560～22 300 m3/s）的洪水期间河槽冲淤过程的分析发现，在流速大到河床处于动平整状态时，洪水过程中主河槽一般表现为涨水期冲刷和落水期淤积，即“涨冲落淤”现象［20－21］；在宽浅河段，受河势影响会出现反常。图5 为黄河下游水文站涨水期流量增幅和河底高程降幅的关系，可以看到流量增大4 000 m3/s 时，河底平均高程冲刷降低0.50 m 左右。河底高程显著降低必然使动床的同流量水位显著低于定床的，而曼宁公式计算很难反映这一现象。

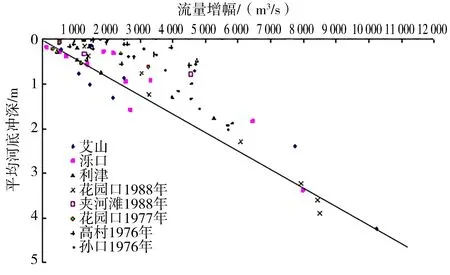
图5 涨水期流量增幅和河底高程降幅的关系

1.4 沙波移动影响的问题

黄河下游河道主槽的河床不但在纵向上极不平坦，在时程上也变化很大，存在沙波运动现象，并且沙波的大小和移动速度随着来水来沙条件的变化而变化。通常在清水冲刷时期起伏大，在来水含沙量较大时起伏较小［22］。

2018 年7 月12 日至16 日小浪底水库实施了排沙，在排沙前的2017 年7 月24 日、2018 年7 月6 日和排沙后的2018 年7 月27 日，三次利用多波束测深系统（MBES）对黄河下游沙波运动状况进行了实地测量。排沙后的2018 年7 月27 日沙浪的最大起伏为1.5 m，和之前的4 m 相比大大减小（见图6），床面变得平整，从而使河槽对水流的阻力显著减小，流速显著提高［23］。

图6 花园口站附近河段的沙波变化

由以上分析可见，曼宁公式根本无法用于计算冲积河流的平滩流量。采用推算水面线的水力计算方法，需要用到河道实测大断面资料，实际上也都存在上述问题。

如果采用数学模型计算，在缺少诸如险工水尺这些实测水位资料时，数学模型无法进行率定和验证，也就无法得到客观可靠的计算结果。在有大量险工水尺资料的情况下，二维数学模型能够反映宽窄相间情况对水面线的影响，但要经过率定和验证，其过程烦琐，涉及网格划分，耗时较长，更何况目前的水沙二维数学模型还无法反映沿程地形起伏的影响。

2 冲积河流平滩流量确定方法

由以上分析可见，影响一个断面同流量水位的因素并不只是本断面形态，而是一个河段。因此，充分利用水文站断面的水位流量过程、水位站或险工水尺的水位过程资料，才能准确确定平滩流量。目前小浪底水库下泄的较大流量超过5 000 m3/s，这和绝大多数河段的平滩流量相差不大。借助实测的水位流量关系略加外延，从而得到平滩流量，这种做法简单直观，这在水文计算上是允许的。而确定大断面平滩流量的关键，除了滩唇高程外，就是如何确定大断面处的洪峰流量和流量涨率。

1）大断面处洪峰流量的确定。洪水在河道内是以波的形式传播的，理论和天然河流的实测资料均显示，在没有区间加水的情况下，受各种因素影响，洪水是逐渐坦化的，洪峰流量沿程减小。黄河下游河道除了伊洛河和东平湖一些年份的汛期向黄河有明显加水外，其他加水很少，而黄河的引水很常见。若不考虑区间加水，则受沿程引水、蒸发和下渗影响，洪峰流量也是沿程逐渐减小的，因此各水文站断面的洪峰流量可依据洪水传播距离按线性插值得到。

2）大断面处流量涨率的确定。影响平滩流量确定的另一个重要因素，是所依据的水位流量关系的斜率，为方便起见，用流量涨率来反映，即水位每变化1 m引起的流量变化，单位为m2/s。影响流量涨率的因素有两个方面：其一是横断面形态，可以大体上以沿程的主槽宽来反映，黄河下游河道虽然从一个短河段看是宽窄相间的，但上游宽下游窄的特点是明显的。根据2020 年汛前大断面，花园口—夹河滩、夹河滩—高村、高村—孙口、孙口—艾山、艾山—泺口、泺口—利津河段的平均槽宽分别为1 445、1 087、651、473、426、394 m。其二为河道比降，高村以上河道比降为0.20‰，高村—艾山河道比降为0.15‰，艾山以下河道比降为0.10‰，纵比降沿程逐渐减小。槽宽逐渐缩窄和河道比降逐渐减缓对水位流量关系的影响是一致的，都是使水位流量关系的斜率逐渐变大，表现在对流量涨率的影响上，就是沿程的流量涨率逐渐减小。根据2019年的实测资料，3 000～5 000 m3/s 洪水时花园口、夹河滩、高村、孙口、艾山、泺口、利津站的流量涨率分别为2 606、2 600、1 930、1 533、1 179、985、852 m2/s，可见流量涨率沿程逐渐减小的特点十分明显。鉴于此，对于没有水位流量关系的淤积断面，其流量涨率可根据上下游有水位流量关系的站按距离进行线性插值得到。

需要说明，受冲淤调整和河势变化的影响，河道的断面形态会发生变化，河槽床沙会发生粗化或细化，从而影响流速，因此在推算当年的平滩流量时应该尽可能采用最新的流量涨率资料。

2.1 实测水位资料较少的情形（方法1）

在沿程水位站或险工水尺较少的情况下，可以充分利用河道淤积断面的测时水位资料。下面以推算黄河下游河道大田楼断面（位于孙口水文站下游约9.88 km）的平滩流量为例，说明详细的推算方法和步骤。

1）统计大断面的测时水位。统计每个断面的2018 年汛前测时水位。大田楼断面2018 年汛前（2018 年4 月25 日）的测时水位为43.79 m。

2）推算大断面的洪水位。统计2018 年汛前大断面统测时水文站、水位站及险工水尺的水位，大田楼断面上游最近的水文站、水位站或险工水尺为孙口水文站，孙口水文站2018 年4 月25 日的水位为45.04 m，汛期最大流量对应最高水位为47.48 m，则二者差值（简称为洪枯差）为2.44 m；大田楼断面下游最近的水文站、水位站或险工水尺为南桥水位站（和南桥大断面位置基本一致，在大田楼下游41.15 km 处），南桥站2018 年4 月26 日的测时水位为39.40 m，汛期最高水位为41.88 m，则洪枯差为2.48 m；粗略地认为同一时间段的洪枯差从上游到下游是线性过渡的，根据大田楼断面距孙口水文站和南桥水位站的距离，计算得到2018 年大田楼断面的洪枯差为2.45 m，则2018 年大田楼断面的洪水位为46.24 m（测时水位43.79 m ＋洪枯差2.45 m）。

3）计算大断面的洪峰流量。大田楼断面上游最近的水文站为孙口水文站，2018 年汛期最大流量为3 960 m3/s；大田楼断面下游最近的水文站为艾山水文站（在大田楼断面下游53.99 km），2018 年汛期最大流量为3 700 m3/s；粗略地认为，受沿程引水、洪水自然坦化、蒸发和下渗影响，洪峰流量从上游到下游是线性过渡的，根据大田楼断面距孙口水文站和艾山水文站的距离，计算得到2018 年大田楼断面的洪峰流量为3 920 m3/s。

4）统计大断面的滩唇高程，计算其在洪水时的出水高度。作图得到大田楼断面的滩唇高程为46.61 m，根据上文得到的洪水位46.24 m，计算二者差值，即滩唇高程比洪水位高0.37 m，称之为断面的洪水出水高度。

5）计算3 000～4 000 m3/s 洪水的流量涨率。根据2018 年的水位表现，在流量为3 000～4 000 m3/s时，上游孙口站的流量涨率为1 179 m2/s，下游艾山站的流量涨率为958 m2/s；粗略地认为，受槽宽向下游不断缩窄的大趋势和比降逐渐减小的大趋势的共同影响，大体上流量涨率沿程线性变化，根据大田楼断面与孙口和艾山的距离，计算得到大田楼断面的流量涨率为1 145 m2/s。

6）计算大断面的平滩流量。大断面的洪水位和洪峰流量为大断面水位流量关系曲线上的一个点。根据上述计算，2018 年汛期大田楼断面的洪水位为46.24 m，流量为3 920 m3/s，流量涨率为1 145 m2/s，洪水出水高度为0.37 m，则大田楼断面的平滩流量为：洪峰流量3 920 m3/s ＋洪水出水高度0.37 m×流量涨率1 145 m2/s＝4 343.65 m3/s，取4 400 m3/s。

2.2 实测水位资料丰富的情形（方法2）

随着物联网和通信技术的发展和普及，黄河下游增设了大量的自记险工水尺。截至2021 年底，黄河下游有有效的险工水尺131 处，加上7 个水文站，则可利用的站点达到138 处，平均间距5.7 km，大体上相当于每隔一个断面就有一处水文站、水位站或险工水尺。丰富的水位资料为准确确定平滩流量提供了极大的便利。

下面以推算2022 年汛前的平滩流量为例，说明如何充分利用水文站水位流量过程、水位站和险工水尺的水位过程推算大断面的平滩流量，主要步骤包括：1）统计大断面的滩唇高程；2）统计2021 年9—10 月洪水（当年流量最大的洪水）水文站、水位站及险工水尺的最高水位和洪峰流量；3）根据大断面的位置，参考上下游水文站、水位站或险工水尺洪水位，按照距离进行线性插值，得到大断面处的洪水位和洪峰流量；4）统计计算水文站断面2021 年9—10 月洪水在较大流量（通常为3 000～5 000 m3/s）时的流量涨率，并根据距小浪底大坝里程，计算得到大断面处的流量涨率；5）将滩唇高程减去洪水位，得到洪水期大断面的出水高度（正数表示滩唇高程高于洪水位，负数表示洪水位高于滩唇高程）；6）将大断面处的洪峰流量加上流量涨率与出水高度的乘积，得到大断面的平滩流量，即大断面的平滩流量初步估算值。

2.3 有关问题的说明

1）方法1 存在的主要问题是测时水位的影响。黄河下游河床质的中值粒径变化范围为0.05～0.20 mm，属于粉细沙，根据沙玉清公式计算得知，这样的泥沙在小流量时很容易起动，但不易悬移输送。根据有关观测和研究，在流量小于1 000 m3/s 时，河床沙波发育，阻力大，且变幅大，同样流量的水位变幅较大，有时还会发生所谓的“假潮”现象（流量不变，水位突然上涨0.3～0.5 m）［24］，而大断面测验时期往往流量较小，因此上述推算的平滩流量难免有误差。解决建议：根据已有研究成果，在流量较大时，河床床面形态为“动平整”，这时候的阻力最小［25］，水位流量关系稳定，水位流量关系的代表性最好，可靠性最高。因此，建议每年在流量为3 000～4 000 m3/s 时，在每个大断面位置测验至少一次水位，据此推算大断面的平滩流量显然更准确。

方法2 与方法1 的差别是不用大断面的测时水位，而是在洪水位水面线上插值，而洪水位期间的流量大，因此方法2 确定的平滩流量的精度显然要高于方法1 的。在目前黄河下游险工水尺资料丰富的情况下，确定平滩流量应直接采用方法2，不再用方法1。

2）黄河下游河道淤积断面虽然目前已经加密到369 个，但就准确计算平滩流量的要求来看，断面间距仍然过大。以彭楼至陶城铺河段为例，平均断面间距3.294 km，孙口与影唐断面间距最小，为2.056 km，而陈楼与龙湾（二）断面的间距长达7.725 km。因此，还要结合野外调研结果最终确定平滩流量。

3）黄河下游河道因其悬河的特点，区间加水的情况较少，上述在介绍平滩流量确定方法时，为简单起见，未提及区间加水的情况。区间加水的情况虽然少但不是没有，例如2021 年汛期孙口站（在东平湖入黄口上游）的最大流量为5 050 m3/s，受东平湖向黄河干流加水影响，相应艾山站（位于东平湖入黄口下游附近）的洪峰流量增大为5 300 m3/s，在推算孙口至艾山河段险工水尺处的洪峰流量时，其下游水文站的洪峰流量应该用艾山的洪峰流量减去同期东平湖入黄的流量。同样，2021 年汛期小花间的伊洛河黑石关站的洪峰流量为2 950 m3/s，沁河武陟站的洪峰流量为2 000 m3/s，在确定伊洛河口和沁河口至花园口河段的大断面洪峰流量时，也应该考虑区间加水。

2.4 平滩流量预估结果的检验

采用上文的方法，对2020 年4 月黄河下游河道的平滩流量进行了预估，预估结果：花园口以上河段一般大于7 200 m3/s，花园口—高村6 000～7 200 m3/s，高村—利津绝大部分河段在4 350 m3/s 以上。随着冲刷的发展，卡口河段最小平滩流量有所增大，增大明显的是卡口河段的上段，即彭楼—葛庄河段，平滩流量自上而下增大了150～400 m3/s，徐沙洼—伟那里河段、梁集—邵庄河段的增幅为100 m3/s，龙湾—赵堌堆及陶城铺附近河段的平滩流量仅增大50 m3/s，陈楼附近的平滩流量未变。最小平滩流量的位置在陈楼—艾山附近河段，最小值为4 350 m3/s［26］。

2020 年汛期，黄河水利委员会组织在黄河下游开展了防洪演练。为实时观测卡口河段的过流能力变化，共组织4 个小组分别对左岸的清河滩和梁集滩、右岸的蔡楼滩和东平滩所在河段进行实时测量。上述4个滩分别对应陈楼断面左岸、大田楼断面左岸、雷口断面右岸和王坡断面右岸，其中陈楼断面位于孙口上游12.46 km，大田楼断面和雷口断面分别在孙口下游9.88 km 和12.77 km，王坡断面在艾山以上16.03 km。测量时间从6 月27 日洪水明显起涨开始，到7 月2 日洪峰过后共历时约6 d。测量期间，孙口的流量从开始的3 430 m3/s 上涨到洪峰流量5 020 m3/s（6 月28 日8：00），落水至7 月2 日的4 460 m3/s，期间孙口的含沙量为5.57～7.00 kg/m3；艾山的流量从开始的3 040 m3/s 上涨至洪峰流量4 800 m3/s（7 月1 日4：54），落水至7 月2 日的4 740 m3/s，艾山的含沙量为6.60～8.88 kg/m3。主要测量出水高度，并根据出水高度和当时的流量推算平滩流量。

表1 为汛前预估平滩流量和实测平滩流量比较，可以看到，实测平滩流量比汛前预估的结果增大0.8%～6.8%，预估略偏安全，且和实际的非常接近［27］。这表明汛前预估值是合理的，采用水位推算平滩流量的方法是可靠的。