干气密封T型槽底部微纹理织构性能研究*

2023-10-07王竞墨丁雪兴王世鹏杨小成丁俊华梁彦兵

润滑与密封 2023年9期

王竞墨丁雪兴王世鹏杨小成丁俊华梁彦兵

(兰州理工大学石油化工学院甘肃兰州 730050)

双向旋转式干气密封因其可以双向旋转具有更加稳定的运行性能[1]，Flowserve公司开发设计的T型槽是目前应用最广泛[2-3]和研究最多的双向旋转槽型之一，已应用在石油化工等领域的高速旋转设备中[4-5]。国内学者也对T型槽进行了深入研究，取得了一系列成果。ZHANG等[6]结合径向基函数法和有限元法，解决了T型槽压力分布问题。白少先等[7]考虑温度引起的端面变形，分析了扰动频率对密封性能的影响规律，发现高参数工况下对T型槽密封性能影响较大。李仁年等[8]考虑微尺度下求解N-S方程，提出基于此的T型槽非线性运动方程，证明了其求解的可行性。彭旭东等[9]将有限单元法应用于求解雷诺方程，得到了在不同转速、压力下的T型槽结构参数的变化规律。

实际应用与理论研究业已证明，干气密封T型槽具有较好的稳定性，但其存在的动压效应不足、摩擦磨损等问题，目前仍未得到有效解决[10]。研究表明，在干气密封双向旋转槽型中增加表面微纹理(织构)，可起到减少摩擦磨损、产生更好的动压效应及密封性能的作用，是目前T型槽研究的又一方向。表面织构是指采用合适的加工工艺，在不改变材料本身的前提下，在其表面制备特定形状、排布和尺寸的微结构阵列，获得特殊的表面形貌，以提升材料物理性能。表面织构(微纹理)这一概念在1966年由HAMILTON等[11]首次提出，目前该概念与技术已成功应用在轴承和密封领域。相关研究表明：表面形貌的合理重构有利于摩擦性能的改善以及提高密封动压效应[12-15]。FALALEEV等[4]将开设微槽的干气密封设备，成功地应用于航空汽轮机中。王衍等人[16-17]基于干气密封微尺度流动特性，在双向干气密封模型基础上进行有无微造型性能分析对比，结果表明，在相同工况下，微造型结构的密封性能较传统结构有明显提升。以上研究虽然证明了表面织构(微槽)对于密封效果有一定提升，但并未进一步对干气密封微纹理织构进行排列造型分类研究与造型设计。

为进一步了解干气密封T型槽不同微纹理设计的密封效果，本文作者基于气膜润滑原理与表面微纹理(织构)构想，并考虑入口压力流向及密封环本身周向旋转的特点，分析一般工况下干气密封T型槽参数对于端面气膜密封性能的影响规律，为双向旋转式端面气膜密封及其微纹理设计提供了参考依据。

1 数学模型建立

干气密封属于非接触式密封，在密封端面开设浅槽，当干气密封正常运转时，介质气体泵吸入微槽内，槽根处的密封坝限制了气体流动，介质气体在槽根处被挤压，进而产生动压效应[18-19]。干气密封运行过程中，动、静密封环间形成了一层很薄但具有刚度的气膜，减少了密封副的碰磨概率。图1所示为常用的干气密封简化系统模型的示意图。

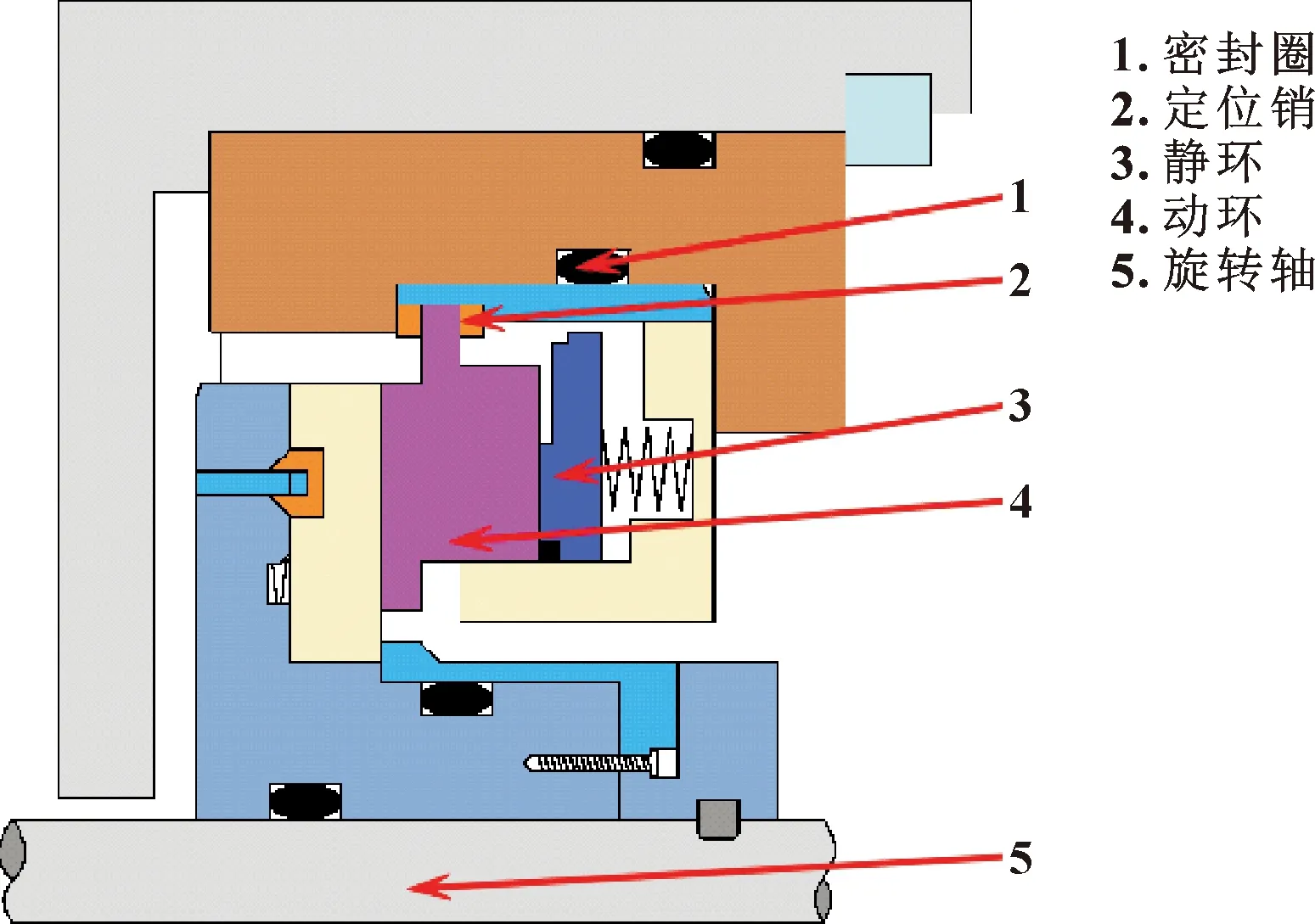
图1 T型槽干气密封端面结构示意Fig.1 Schematic of T-groove dry gas seal end face structure

1.1 T型槽微纹理设计

T型槽是干气密封动环或静环端面上开设有形如字母“T”的槽型，干气密封T型槽结构如图2所示。可见T型槽结构具有对称性，理论上其环内各区域流场相同，所以在数值计算过程中选取一周期区域进行计算。

图2 干气密封T型槽立体结构Fig.2 Three-dimensional structure of T-groove dry gas seal

干气密封T型槽平面示意图及微纹理结构如图3所示。考虑入口压力流向及密封环本身周向旋转的特点提出4种形式不同的微纹理结构：Type 1径向微纹理(radial-micro)，Type 2周向微纹理(circumferential-micro)，Type 3径-周向微纹理(longitudinal-transverse)，Type 4周-径向微纹理(transverse-longitudinal)。

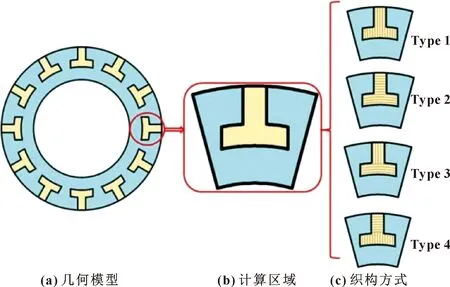
图3 干气密封T型槽及微纹理结构示意Fig.3 Schematic of T-groove structure of dry gas seal：(a)geometric model；(b)calculation area；(c)texture pattern

1.2 压力控制方程建立

对于气膜密封问题的相关计算参考相关文献[20-21]，并计算基于如下假设：

(1)忽略体积力、惯性力的作用；

(2)介质气体在密封端面间无明显滑移；

(3)介质气体黏度和密度在膜厚方向不变化；

(4)润滑剂为牛顿流体(等温、等黏度)。

1.3 边界条件、连续性、流态判断

基于上述假设，在密封端面上得到满足质量守恒的极坐标下的稳态Reynolds方程为

(1)

式中：r为端面气膜上任意一点半径，mm；θ为展开角度，rad；h为密封间隙，μm；μ为介质黏度，Pa·s；ω为角速度，rad/s。

参考文献[22]设定压力边界条件：

p(ri，θ)=pi；p(ro，θ)=po

(2)

式中：ri为密封环内径；ro为外径；pi为入口处压力；po为出口处压力。

周期边界条件：

(3)

式中：Ng为槽数。

连续性及流态判断：已知干气密封端面间液膜厚度为微米级，参考流动因子对液膜所处的流态进行判别，端面内流体流态设为层流[23-24]。

得到整个密封端面或者周期性结构的压力分布为

(4)

各系数表达式为

2 T型槽仿真计算方法

2.1 控制方程离散及精度要求

参照文献[25]确定超松弛(SOR)格式及松弛因子，计算公式如下：

(5)

松弛因子Ω在流体润滑问题中一般取1.5～1.8，文中取1.6。

超松弛迭代的计算结果满足式(6)要求时，说明对于压力场求解完成，边界条件如图4所示。

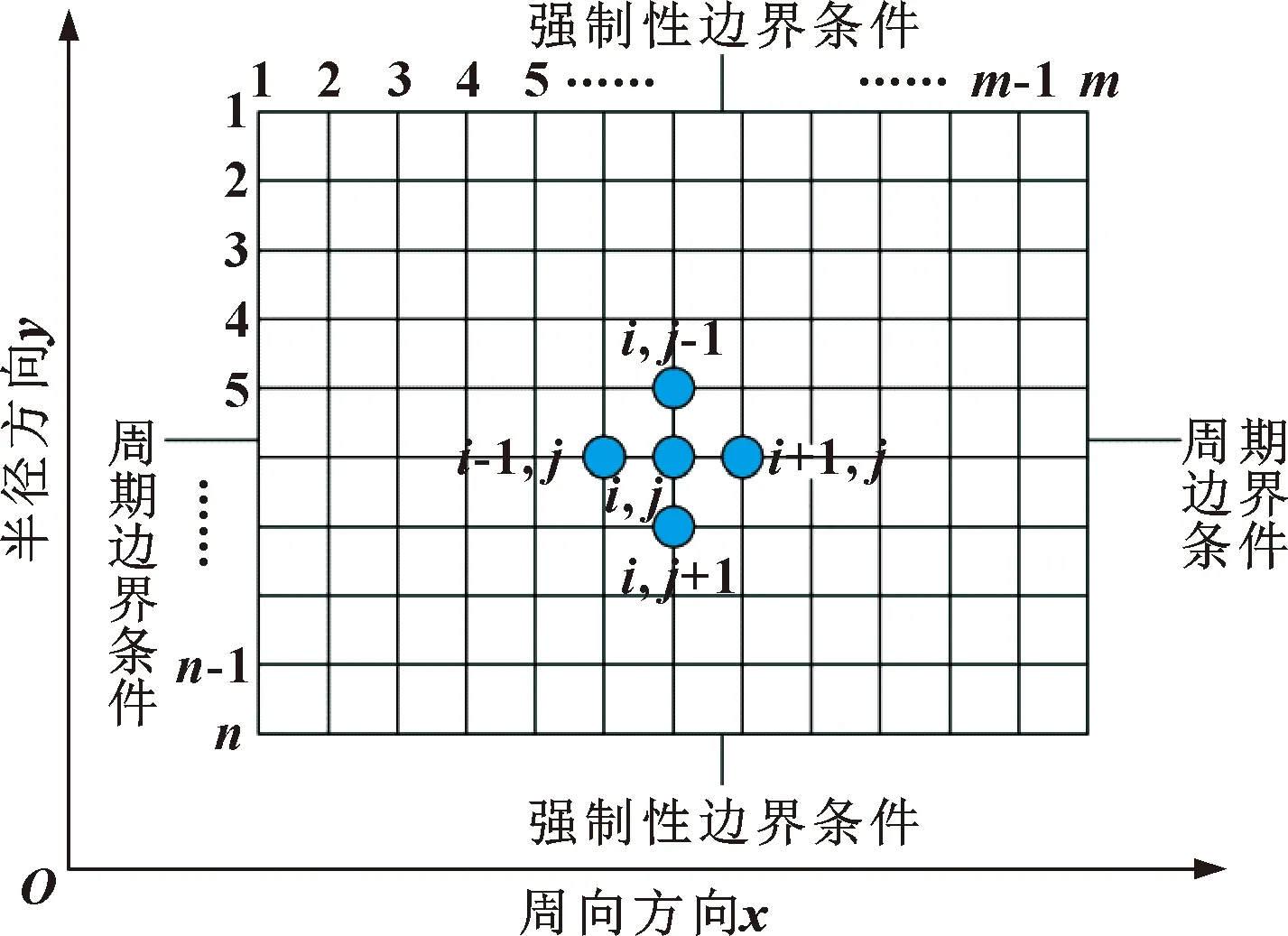
图4 强制性边界条件Fig.4 Mandatory boundary conditions

(6)

气体密封的密封介质具有可压缩性，并且压力呈非线性，因此在求解过程中无法得到具体解析解，通常使用数值法进行求解。文中所使用的求解方法为有限差分法。

2.2 目标参数计算公式

(1)开启力

(7)

式中：ro为密封环外径；ri为密封环内径。

(2)泄漏量

(8)

2.3 计算流程

密封介质为空气，保持出口压力为1个标准大气压(0.1 MPa)，介质黏度μ为1.844 8×10-5Pa·s不变，不考虑加工过程引起的槽区粗糙度变化、摩擦磨损，以转速、进口压力、平均气膜厚度、微纹理深度为自变量，计算4种微纹理结构与微无纹理结构T型槽的开启力、泄漏量。计算流程如图5所示。

图5 计算流程Fig.5 Calculation flow

2.4 网格无关性验证

选取1/Ng的计算域、未开设微造型T型槽进行验证。在MATLAB软件中通过划分不同网格数量进行网格无关性验证，开启力(FO)和泄漏量(Q)受网格数量的影响最明显，而这两者也是判断密封性能最重要的依据之一。保持入口压力1 MPa、转速10 000 r/min、气膜厚度3 μm、槽数12不变，改变网格数分析了对开启力和泄漏量的影响，结果如图6所示。可以看出，当网格数量由110×110变为120×120时，开启力和泄漏量变化幅度已不大，分别为0.003 3%和0.004%，然而所用时间由475 s大幅上升至1 680 s。因此，考虑计算速度与准确性，文中选取110×110的网格密度。

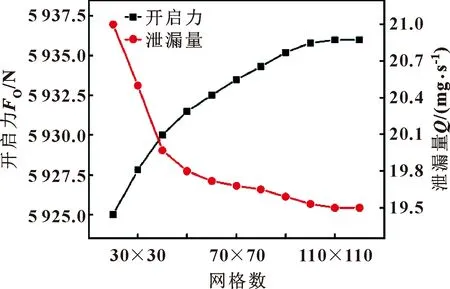
图6 网格数对开启力、泄漏量的影响Fig.6 Influence of grid number on opening force and leakage

2.5 计算模型验证

为验证文中数学模型与计算方法正确性，按文献[26]中的几何结构参数与试验工况参数(见表1)，计算未开设微纹理的干气密封T型槽在不同气膜厚度下的开启力。图7示出了文中数值解和文献试验值的比较。

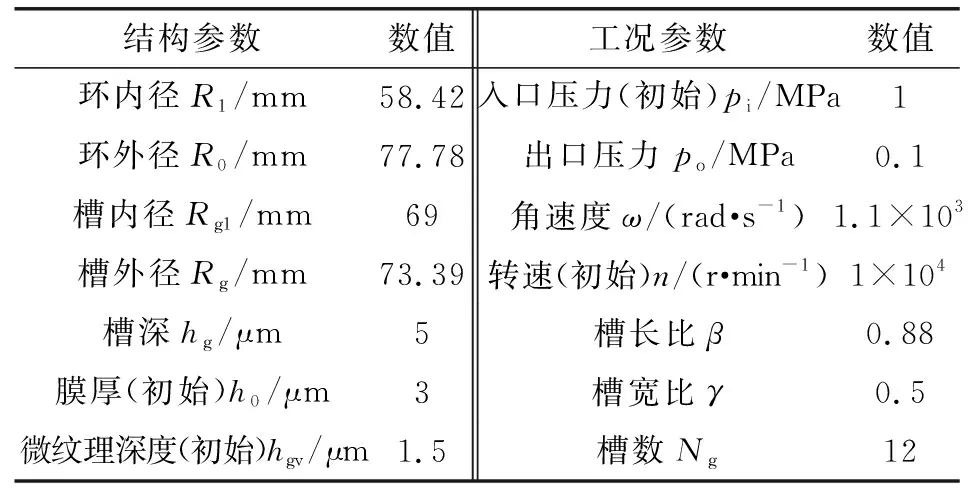
表1 干气密封T型槽结构参数与工况参数Table 1 Structural and working condition parameters of T-groove dry gas seal

图7 不同气膜厚度下文中开启力数值解和文献试验值的比较Fig.7 Comparison between numerical solution of opening force and experimental value in literature under different film thickness

由图7可见，文中数值解和文献试验值最大误差出现在气膜厚度6 μm处，且误差不超过9%。文中数值解和文献试验值变化趋势一致，可以证明文中计算结果的准确性。造成误差的主要原因，一是实际气体与理想气体之间的差别以及试验中气体平均分布不均匀，二是文献中T型槽做了一定角度改变，另外文献[26]中设定的工况参数为最高压力0.5 MPa、转速6 000 r/min，与文中设定有一定区别。

3 计算结果与讨论

3.1 气膜厚度与压力分布

T型槽在圆环内呈周期分布，在MATLAB软件编程中选取单周期进行计算，得到无微纹T型槽与4种微纹理造型T型槽单周期膜厚、压力计算结果如图8、9所示。

图8 无微纹理T型槽单周期气膜膜厚、压力分布Fig.8 Single period film thickness(a)and pressure(b) distribution of T-groove without microtexture

在稳态计算过程中，气膜厚度不随时间发生变化，即气膜厚度分布为初始参数确定后计算得到的结果。从图8(a)可以看到，非槽区气膜厚度为3 μm，槽区气膜厚度分布明显凸起。在与压力控制方程耦合求解时，计算程序会对气膜分布矩阵中的每个节点值循环取值计算。由图8(b)所示的轴侧方向的气膜压力分布可以看出，气膜压力从进口处逐渐上升，在压力达到最高值后，气膜压力随着径向半径的减小而先增大后减小，对应图8(a)中的气膜厚度分布。

图9所示为4种带有有序微纹理设计的T型槽气膜膜厚分布，可以看到在相同T型槽基底的基础上，可视化立体图中4种微纹理设计的区别。在稳态计算过程中，气膜厚度同样不随时间发生变化，因有序微纹理设计压力分布在形貌与纵坐标范围下数值区别不明显，故文中未列出其压力分布。

图9 4种微纹理T型槽单周期气膜膜厚分布Fig.9 Single period film thickness distribution of T-grooves with four types of microtexture： (a)Type 1；(b)Type 2；(c)Type 3；(d)Type 4

3.2 转速对密封性能的影响

在压力1 MPa、平均气膜厚度3 μm、微纹理深度1.5 μm条件下，研究了开启力、泄漏量随转速的变化趋势，结果如图10所示。可以看出，开设微纹理槽型与未开设微纹理槽型的开启力、泄漏量随转速的变化规律一致，但开设微纹理槽型与未开设微纹理槽型相比，开启力明显增大，泄漏量明显减小。如图10(a)所示，开启力随转速增加呈抛物线形式增长，因为随转速增加，槽内动压效应增强，因此开启力整体增大；Type 1和Type 3结构、Type 2和Type 4结构开启力数值相近，Type 3结构产生的气膜开启力更大。如图10(b)(c)所示，泄漏量随转速增加而略微减小(最大值与最小值相差2×10-6)，说明转速不是引起泄漏量变化的主要因素，但随着转速提高，线速度提高，离心惯性力阻碍气体流动，一部分将要溢出的气体被向心力带回，因而泄漏量略微减小。开设微织构槽型相比于无微织构槽型，泄漏量减小约75%，Type 3结构泄漏量在转速变化过程中总体最小。

图10 开启力、泄漏量随转速的变化Fig.10 Changes of opening force and leakage with rotation speed：(a)rotation speed vs opening force；(b)rotation speed vs leakage (4 types of microtexture grooves)；(c)rotation speed vs leakage(without microtexture groove)

对比4种微纹理槽型仿真结果可知，在不同转速下，在开启力与泄漏量方面均是Type 3结构(纵-横微纹理结构)表现最佳。

3.3 压力对密封性能的影响

在转速10 000 r/min、平均气膜厚度3 mm、微纹理深度1.5 μm条件下，出口压力保持1个大气压(0.1 MPa)不变，改变进口压力，研究了开启力、泄漏量随进口压力的变化趋势，结果如图11所示。可以看出，开设微纹理槽型与未开设微纹理槽型的开启力、泄漏量随入口压力的变化规律一致。如图11(a)所示，开启力随压力增大呈线性增长，由于进口压力的增大使密封环内外压差增大，加快密封区域流体向低压侧流动，动压效果增强，开启力增大，说明压力是影响开启力变化的主要因素。4种微纹理槽型中，Type 3结构所产生的开启力最大，无微纹理槽型处在4种微纹理槽型中间位置。如图11(b)(c)所示，泄漏量随压力增大而增大，泄漏量增加是由于进口压力增大使得密封环内外压差增大，压差增加导致密封介质向低压侧流动，因此泄漏量变大。开设微织构槽型相比于无微织构槽型泄漏量明显减小，其中Type 4结构泄漏量最小，但4种微织构槽型泄漏量相差不大(最大相差5×10-6)，无微纹理槽型处在4种微微织构槽型中间位置。

图11 开启力、泄漏量随入口压力的变化Fig.11 Changes of opening force and leakage with inlet pressure：(a)pressure vs opening force；(b)pressure vs leakage

对比4种微纹理槽型可知，随压力升高，开启力与泄漏量均有明显提升，但二者的数量级不同，因此以浮漏比(开启力/泄漏量)为参量，随压力升高，T型槽动压效果更好，且Type 3结构(纵-横微纹理结构)整体表现更好。

3.4 气膜厚度对密封性能的影响

在转速10 000 r/min、进口压力1 MPa、微纹理深度1.5 μm条件下，改变平均气膜厚度，研究了开启力、泄漏量随平均气膜厚度的变化趋势，结果如图12所示。可以看出，4种微纹理T型槽随平均气膜厚度的变化规律一致，而无微纹理T型槽随气膜厚度增加变化不明显。如图12(a)所示，开启力随气膜厚度增加而减小，这是因为平均气膜厚度增加，密封间隙增大，动压效果减小，因而开启力呈抛物线性减小。4种微纹理槽型中，Type 2结构的开启力减小最大，当气膜厚度到达6.5 μm后，Type 2、4开启力小于无微纹理T型槽。如图12(b)(c)所示，泄漏量随气膜厚度增加而略微变大(变化为6×10-6)，这是因为平均气膜厚度增加，密封间隙变大，因此泄漏量变大。开设微织构槽型相比于无微织构槽型泄漏量明显减小(最大值相比较减小约80%)，Type 2和Type 4结构、Type 1和Type 3结构泄漏量数值相近，Type 2结构泄漏量整体最大。

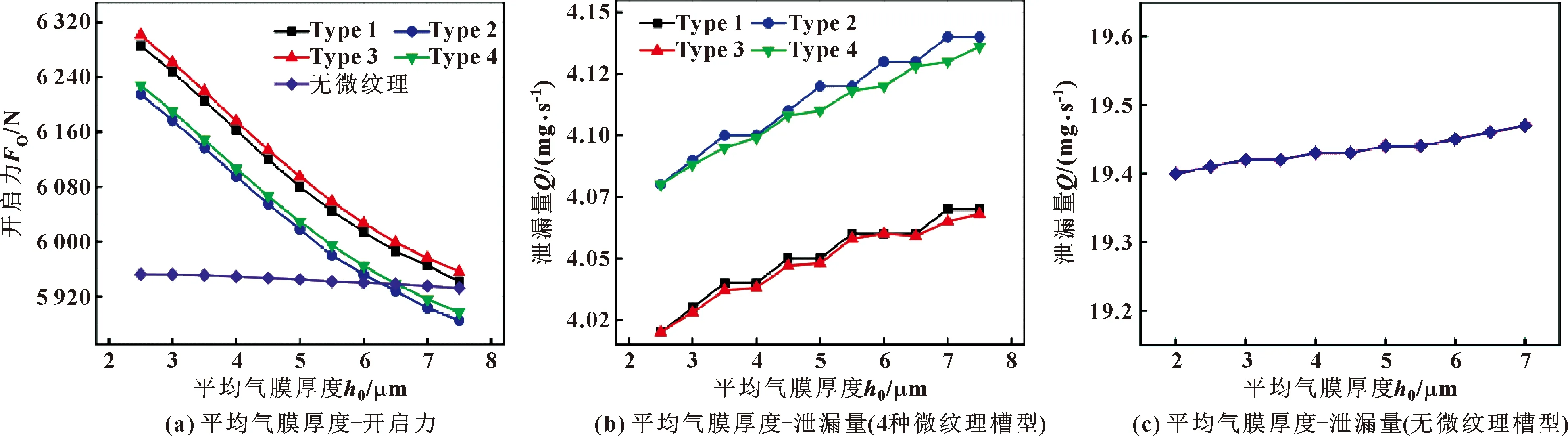
图12 开启力、泄漏量随气膜厚度的变化Fig.12 Changes of opening force and leakage with film thickness：(a)average film thickness vs opening force；(b)average film thickness vs leakage(4 types of microtexture grooves)；(c)average film thickness vs leakage(without microtexture groove)

3.5 微纹理深度对密封性能的影响

在转速10 000 r/min、进口压力1 MPa、平均气膜厚度3 μm条件下，改变微纹理深度，研究了开启力、泄漏量随微纹理深度的变化趋势，结果如图13所示。如图13(a)所示，随微纹理深度增加开启力总体呈上升趋势，这是因为微纹理深度增加，使得动环槽区与静环距离减小，类似于气膜厚度减小，槽区间隙减小，动压效果增强。4种微纹理槽型中，Type 1、3结构开启力增加明显，Type 3结构开启力数值最大；Type 2、4结构在微纹理深度到达1.5 μm后动压效果减弱，开启力增量减小。如图13(b)所示，随微纹理深度增加泄漏量总体呈上升趋势，这是因为微纹理深度增加，使得槽区与非槽区高度差进一步变大，使气体泄漏溢出，其中Type 2结构泄漏量整体增加最大。

图13 开启力、泄漏量随微纹理深度的变化Fig.13 Changes of opening force and leakage with microtexture depth：(a)microtexture depth vs opening force：(b)microtexture depth vs leakage

综上所述，具有微纹理织构的T型槽在同等工况参数变化的情况下对开启力提升、泄漏量减小效果明显，可能原因是微纹理织构本身具备一定的导流介质气体效果，对于径向流速起到减弱作用。T型槽槽型较宽，本身导流效应较弱，因而设计微造型结构对该类槽型的流动有序性改善效果更加明显，尤其在Type 3结构中，介质气体随径向纹理导流，在启动阶段被周向纹理环绕更少溢出，因此Type 3结构(纵-横微纹理结构)T型槽动压效果最好。

文中计算结果与文献[16]相比较可间接验证计算结果合理性。对比4种微纹理T型槽可知，在相同工况情况下，纵-横微纹理结构(Type 3结构)开启力更大、泄漏量更小，因此密封性能更好；径向微纹理结构(Type 1结构)相比于周向微纹理结构(Type 2结构)所产生的效果更好；复合结构(Type 3纵-横微纹理结构)相较于单一结构(Type 1径向微纹理结构 )效果更好。