ITER 第一类边界局域模对排布位错偏滤器靶板钨/铜瓦片腐蚀程度的数值模拟*

黄艳 孙继忠 桑超峰 王德真

1) (大连工业大学基础教学部,大连 116034)

2) (大连理工大学物理学院,大连 116024)

偏滤器靶板钨/铜瓦片在高热流作用下的热表现是未来托卡马克ITER 最受关注的问题之一.由于安装精度等因素,钨/铜瓦片会出现排布位错从而产生凸出棱边,凸出棱边处能流密度极大,严重侵蚀靶板.建立了二维对流传热的自洽模型,包括热辐射、汽化和熔化效应,同时,耦合冷却水状态变化,研究类ITER 第一类边界局域模热流对出现排布位错的偏滤器靶板钨/铜瓦片的腐蚀程度,比较直角、斜边瓦片的热性能.为了研究瓦片缝隙、排布误差对等离子体行为和能流密度分布的影响,利用二维边缘等离子体动理学程序计算不同排布误差下两种形状瓦片表面的能流密度分布,并作为热传导模型的输入参数.研究结果表明: 瓦片缝隙附近等离子体行为会受排布误差影响,不同排布误差下的直角、斜边瓦片边缘处能流密度分布不同,对两种形状瓦片的热表现影响极大,排布误差越大,两种形状瓦片的热腐蚀程度越大;相对于直角瓦片,斜边瓦片在边界局域模热流作用下的热腐蚀程度较小,且有较好的对抗排布位错的能力.

1 引言

钨(W)材料作为ITER 偏滤器靶板的壁面材料,具有热导率高、熔点高和氚滞留率低等优点[1,2].但是,钨材料在高热流作用下会出现裂纹和熔化,为了减小等离子体热负荷和感应电流引起的应力,ITER 偏滤器靶板现在被设计为便于拆除和可重复使用的瓦片结构[3],上部为钨材料,内部冷却管为铬锆铜(CuCrZr),中间过渡层为铜(Cu).

瓦片结构在实际安装过程中由于加工工艺和安装精度的限制,以及运行过程中振动等因素,会导致在垂直偏滤器靶板表面方向上瓦片实际位置与设计值之间存在偏差,称其为径向排布位错,位错值称为排布误差(δ).显然,出现位错时,直角瓦片会产生凸出棱边,如图1(a)所示,环向方向凸出棱边与磁感线几乎垂直,使凸出棱边处的入射等离子体能流密度大大增加.为了检验钨瓦片的热表现,在2014 年,EAST 上偏滤器靶板升级为钨,瓦片结构与ITER 类似,测量发现: 70%–75%瓦片,δ≤ 0.5 mm;20%–25%瓦片,0.5 <δ≤ 1 mm;2%–5%瓦片,1 <δ≤1.5 mm[4],δ越大,等离子体能流越大.ITER 组织对制造方提出相邻瓦片允许的最大排布误差为0.3 mm[5].

图1 排布位错瓦片结构示意图 (a)直角瓦片;(b)斜边瓦片Fig.1.Schematic diagram of misalignment tile structure: (a) Unshaped tile;(b) beveled tile.

为了解决钨/铜瓦片环向凸出棱边问题,ITER偏滤器靶板瓦片拟采用斜边形状,最简单的做法是将瓦片上表面在环向方向向下倾斜,如图1(b)所示,倾斜深度在内外靶板上为0.5 mm,此时,即使相邻瓦片间的排布误差为0.3 mm 时,依然可以屏蔽约3 mm 的区域[6],因此消除了环向方向因排布位错而产生的凸出棱边.但该方法的问题是,斜边瓦片由于顶角(β)的存在,磁力线与瓦片表面的夹角增加,斜边瓦片上表面没有屏蔽区域的等离子体能流密度会增加 sin(β+α)/sinα倍(α为磁场与瓦片表面的夹角),在热辐射功率可忽略的条件下,表面温度基本与入射等离子体能流密度成正比,即瓦片表面温度也将升高约 sin(β+α)/sinα倍.

EAST 运行中发现在稳态能流密度为3 MW·m-2时,钨/铜瓦片极向缝隙棱边、铜材料和铬锆铜冷却管出现了熔化,研究结果表明是凸出棱边导致的能流密度增加造成的[7].ITER 所允许的最大稳态能流密度为10 MW·m-2,而且ITER 每次放电将会发生103个以上的第一类边界局域模(edge localized modes,ELMs)[8],发生ELMs 时,大量的能流和粒子流会在几百微秒的时间里从中心等离子体区域沉积到偏滤器靶板的狭窄区域上[9],侵蚀靶板.位错瓦片凸出棱边沉积的大量能量会大大加重ELMs热流对瓦片的热腐蚀程度[4,7].

Bazylev 等[10-12]建立了MEMOS 模型,研究钨材料在ELMs 高能流下的温度分布,以及汽化、熔化和熔化层流动等问题,但没有考虑瓦片位错问题和瓦片缝隙对等离子体性质的影响.Wang 等[4]和 Chen 等[13]模拟了不同排布误差下的多种形状瓦片在等离子体能流作用下的温度分布,评估其热表现.Li 等[7]模拟了不同排布误差下双倒角钨/铜瓦片的热表现.这3 项研究中利用单相强制对流的Dittus-Boelter 准则计算对流传热系数,但是冷却水状态满足Bergles-Rohsenow 修正时,冷却水状态转为过冷沸腾[14,15],传热系数会发生较大变化,ITER 运行参数高于EAST,且发生第一类ELMs时能流密度为1–10 GW·m-2[16],需要考虑冷却水状态变化,而且,这3项研究工作也没有考虑瓦片缝隙对等离子体性质的影响.文献[17-22]中的工作表明,瓦片缝隙处的等离子体行为会发生变化,缝隙附近的能流密度会重新分布,能流密度决定了偏滤器靶板瓦片的侵蚀程度,所以这种效应不能忽略.Gunn 等[18]利用离子轨道模型方法,计算不同形状钨瓦片缝隙区域的能流密度分布,采用一维传热模型计算钨瓦片在类似ITER 的ELMs 能流作用下的温度分布,然后利用修正因子进行修正.

本文在前期工作[23,24]基础上,将热传导模型与冷却水状态相耦合建立二维对流传热模型,冷却水状态考虑了单相强制对流和两相核沸腾,研究排布误差为0–0.3 mm 的位错偏滤器靶板直角、斜边瓦片在类ITER 第一类ELMs 高热流下的热表现,评估两种形状瓦片的热性能,同时,考虑不同排布误差下的直角和斜边瓦片缝隙引起能流密度的不均匀性对瓦片腐蚀程度的影响.瓦片内部冷却管材料为铬锆铜,中间过渡层为铜,外部为钨,各部分尺寸见图1.

2 计算模型

本文研究工作由两部分内容组成: 第1 部分是利用二维边缘等离子体动理学程序(2d3v PICMCC)[21,22]研究不同排布位错下直角和斜边瓦片缝隙对等离子体性质的影响,计算打到瓦片表面不同位置的能流密度分布;第2 部分采用热传导模型,以2d3v PIC-MCC 模型的计算结果作为输入参数,考虑熔化、汽化和热辐射效应,研究ELMs热流对直角和斜边钨/铜瓦片的腐蚀程度.粒子模拟/蒙特卡罗碰撞(PIC/MCC)模型的基本思想是模拟跟踪带电粒子在实际位形下的等离子体中的运动,并采用蒙特卡罗技术处理粒子间碰撞,从而得到其能量分布函数,进而得到感兴趣的物理量,细节请参考文献 [25,26].下面详细介绍二维热传导模型.

本文靶板瓦片的热表现利用Multiphysics CO MSOL 传热模块二维热传导模型和变形几何模块进行模拟研究.瓦片上表面以能量平衡方程作为边界条件:

(1)式中,-k(∂T/∂n)表面为传导到瓦片内部的热通量,(∂T/∂n)表面为温度梯度,T为表面处温度,n表示表面法线方向,k=1/(aT+b)[27,28]为热传导系数,对于钨材料a=1.70×10-6m·W-1,b=6.41×10-3m·K·W-1[28];右侧第1 项是入射到瓦片表面的热通量;第2 项和第3 项分别是汽化和热辐射损失的热通量.(2)式中,Ai和Bi为两个常数,对于钨材料分别为44485 K 和12.74[16];Mi为钨的原子质量;Lv为汽化潜热.(3)式中,ε为发射系数,本文取0.4;σ是斯蒂芬玻尔兹曼常数;TS表示靶板表面的温度;T0表示靶板表面没有受到等离子体能流照射部分的温度.

瓦片侧面的边界条件为

冷却管内壁表面传热系数的计算包含了冷却水的单项强制对流和两项核沸腾状态,计算方法分别如2.1–2.3 节所述.

2.1 单项强制对流

在冷却管内壁边界条件为

其中,Tb为冷却水温度;Tin为冷却管入口处温度;q为传导入冷却管的能流,单位为W;G为质量流速;Cp为比热;A为冷却管截面面积.(5)式左端为冷却管内壁面对流热通量,等式右端TW为壁面温度,h为传热系数.根据冷却水状态不同,采用不同的计算方法计算传热系数h.

1)当冷却水处于紊流状态(Re≥10000),利用Dittus-Boelter[29]准则来计算Nu:

式中d为冷却管直径,Re为雷诺数,Pr为普朗特数.

2)当冷却水处于层流状态(Re≤ 2100),利用Sieder-Tate[30]准则来计算Nu:

式中L为冷却管长度,µb和µW分别为冷却水温度和管壁温度下的水动力黏度.

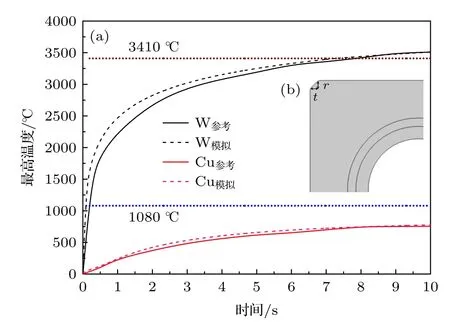
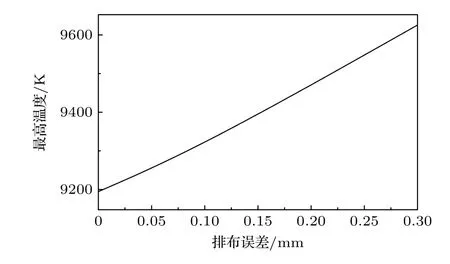
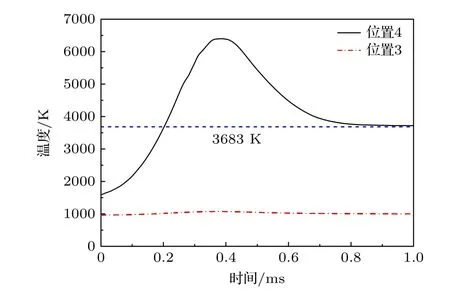
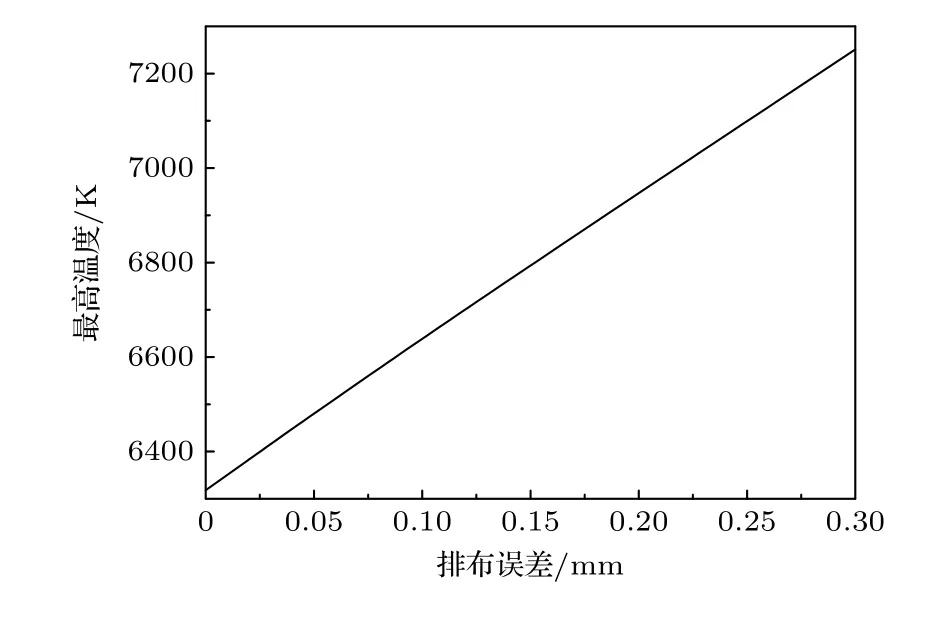
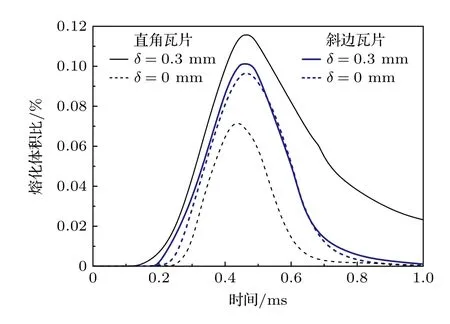
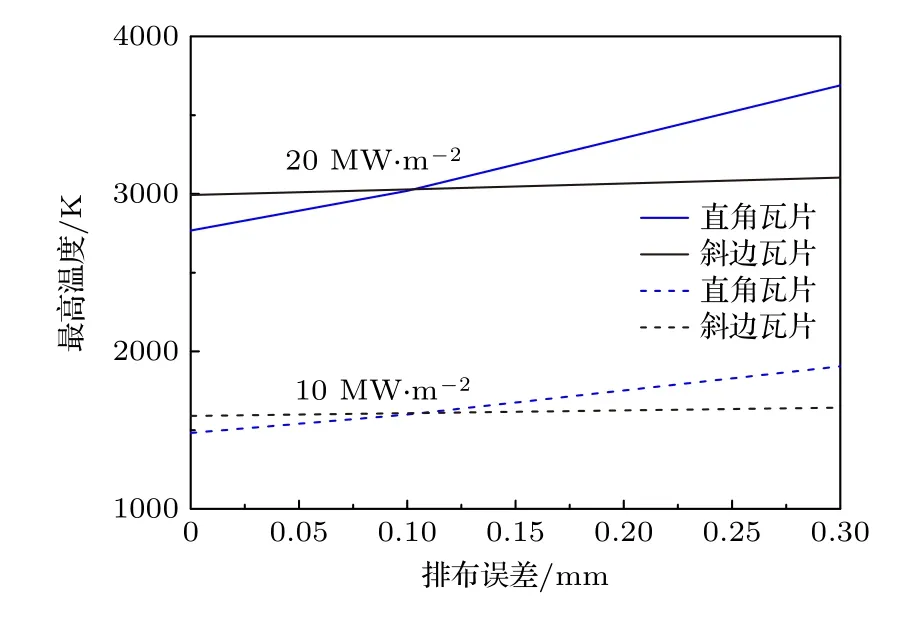
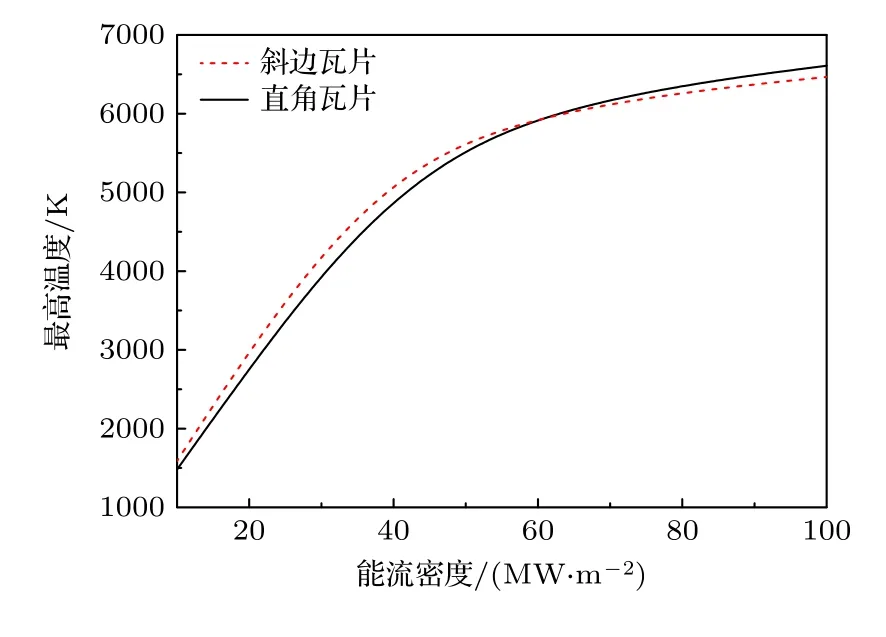
3)当冷却水处于层流与紊流过渡阶段状态(2100

式中Prb和PrW分别为冷却水温度和壁温度下的普朗特数.

2.2 过冷沸腾

当冷却管内壁温度达到过冷沸腾的起始温度(TONB,下标“ONB”是过冷沸腾起始点onset of nucleate boiling 的缩写),过冷沸腾开始,TONB可以利用Bergles 和Rohsenow 准则进行计算[31]:

式中,p为冷却水压强,单位为bar (1 bar=105Pa);Tsat为冷却水饱和温度;为在TONB时的能流密度,单位为W·m-2.

过冷沸腾时通过冷却管内壁的热通量写为[32]

式中,hSP和hNCB分别为单项强制对流和饱和沸腾传热系数,具体表达式为[32]

(12)式中u为冷却水流速,ρ为冷却水密度,μ为冷却水动力黏度;(13)式中,下标“l”和“v”分别代表液相和气相;ζ是水的表面张力,单位N/m;△Tsat=Tw-Tsat,表示管壁过热温度;△Psat是与△Tsat相对应的压强差;S称为核沸腾抑制因子,流速为0时S≈ 1,流速为无穷大时,S≈0,在Re≤ 325000时,S计算式为[33]

2.3 饱和沸腾

冷却水达到饱和沸腾时,传热系数hsat为[25]

此时,核沸腾抑制因子需要考虑水蒸气质量,具体关系式可以参考相关书籍和文献[31,32].

3 模拟结果

3.1 模型验证

为了验证物理模型的合理性,首先将本理论模型与已有模拟结果比较.在文献[7]中,66 MW·m-2的平行热流(q//)作用于排布误差为2.5 mm 的EAST双倒角瓦片表面,即瓦片上表面垂直热流密度为q//sinα=1.5 MW·m-2,瓦片斜边上的热流为q//sin[α+arctan(r/t)],r为倒角径向尺寸,t为倒角环向尺寸,如图2(b)所示,r和t均为1 mm,凸出棱边处热流密度为q//cosα,磁感线与瓦片表面夹角为1.3°,热流沉积时间为10 s,水冷条件为压强1 MPa,流速3 m·s-1,水温100 K,钨材料和铜中间层最高温度随时间变化关系见图2(a).图2(a)实线为文献中结果,虚线为本模型计算结果,钨材料和铜中间层最高温度随着时间迅速升高,时间7.7 s 左右钨材料最高温度超过熔点,铜中间层最高温度始终低于其熔点,两项工作的结果吻合较好.但是该工作是利用光学近似方法计算瓦片表面能流密度分布,该方法不考虑带电粒子的回旋运动与鞘层电场等因素对粒子分布的影响,计算的能流分布不够准确[15-20].本文以下研究采用2d3v PICMCC 模型[21,22]考虑瓦片和瓦片间形成的不连续几何结构对附近的等离子体行为和瓦片表面各处沉积的能流密度的影响,准确地给出瓦片表面的能流密度分布.

图2 (a)双倒角瓦片钨材料和铜中间层最高温度模拟结果与现有工作[7]的对比,排布误差为2.5 mm,表面热负荷为1.5 MW·m-2;(b)四分之一双倒角瓦片结构图Fig.2.(a) Temporal evolution of the highest temperature of W armor and Cu heat sink materials of dual chamfer tile for misalignment of a 2.5 mm and perpendicular heat flux of 1.5 MW·m-2.Here the calculated results are represented by the dash lines,and those represented by the solid lines are taken from the work by Li et al.[7];(b) schematic diagram of quarter dual chamfer tile.

3.2 能流密度分布

本研究2d3v PIC-MCC 模型的模拟参数为:径向排布误差(δ)为0–0.3 mm,瓦片间缝隙为0.5 mm,瓦片环向、径向宽度都为28 mm,瓦片参数详见图1,等离子体密度ne=ni=1.0×1021m-3,电子和离子温度Te=Ti=5 eV,磁场与瓦片表面夹角5°,磁场强度6.0 T[34-36],入射能流密度为10 MW·m-2.图3 给出了δ为0 和0.3 mm 的直角、斜边瓦片表面各点的能流密度分布.从图3 可以看出,直角瓦片表面中心区域能流密度的分布基本不受瓦片缝隙和位错影响,瓦片间缝隙改变了附近等离子体的性质,导致瓦片边缘处能流密度较大,且随排布误差的增加而增大,当δ=0 时,面向入射等离子体一侧的棱边区域(图1 位置1 区域)能流密度基本为入射等离子体能流密度的2.5 倍,背向入射等离子体一侧棱边处(图1 位置2 区域)能流密度也有增加,约为入射等离子体能流密度的1.06倍,源于瓦片缝隙入口处“电势峰”导致的能流密度重新分布,但是其值小于图1 所示位置1 区域能流密度;当δ=0.3 mm 时,两棱边区域能流密度分别约为入射等离子体能流密度的3.6 倍和1.3 倍,缝隙内从瓦片表面到底部能流密度迅速衰减.斜边瓦片面向入射等离子体一侧棱边区域(图1 位置3区域)因为相邻瓦片的磁遮挡,能流密度极小,随着排布误差的增加,该区域能流密度会随之增加,背向入射等离子体一侧棱边处(图1 位置4 区域)能流密度极大,排布误差越大位置4 区域能流密度越大,当δ=0 时,其约为入射等离子体能流密度的1.52 倍;当δ=0.3 mm 时,其约为入射等离子体能流密度的1.66 倍,且能流密度由位置4 向瓦片中心区域逐渐减小.2d3v PIC-MCC 模型的计算结果显示,δ从0 增大到0.3 mm,无论是直角瓦片,还是斜边瓦片,两侧棱边区域能流密度都有增加,但是相比于直角瓦片,斜边瓦片受径向排布位错的影响较小,说明为防止凸出棱边处入射等离子体能流密度大幅增加,将瓦片上表面在环向方向向下倾斜是有效的方法.

图3 偏滤器瓦片表面能流密度分布 (a) δ=0 的直角瓦片;(b) δ=0.3 mm 的直角瓦片;(c) δ=0 的斜边瓦片;(d) δ=0.3 mm的斜边瓦片;坐标系原点取在瓦片中心,距离值表示沿着瓦片表面距离瓦片中心的距离,向右为正,向左为负Fig.3.Energy fluxes received by divertor tile: (a) Unshaped tile for δ=0;(b) unshaped tile for δ=0.3 mm;(c) beveled tile for δ=0;(d) beveled tile for δ=0.3 mm.Origin of coordinate frame is set at tile center,absolute coordinate value is distance along surface away from center;sign ‘+’ denotes direction to right,and sign ‘-’toleft.

前期研究中[24],根据ELMs 间隙间和ELMs过程中排布误差为0 的直角瓦片表面各点能流密度的分布,发现无论入射等离子体能流密度具体是多少,直角瓦片表面各点的能流密度分布规律基本相同,或者说,等离子体能流密度在瓦片表面各点的分布与入射等离子体能流密度的具体数值没有直接关系,进一步可以得出这样的结论: 无论是直角、还是斜边瓦片,在ELMs 间隙间和ELMs 过程中,瓦片表面各点能流密度的比值关系相同[37].本研究ELMs 过程中的能流密度分布规律是根据ELMs间隙间能流密度分布相应地进行数值放大,但这一简化处理,有必要结合实验结果,在今后工作中进一步改进.

未来ITER 发生ELMs 时打到偏滤器靶板的能量预期为1–3 MJ·m-2,沉积时间为 0.1–1.0 ms,稳态运行时打到靶板的能流密度预期为5–20 MW·m-2[38,39].本研究中ELMs 间隙间能流密度取10 MW·m-2,ELMs 能量取1 MJ·m-2,持续时间为600 μs (能量上升和下降时间各为300 μs)[16],随时间变化规律为高斯分布,如图4 所示.ELM过程瓦片的初始温度分布利用间隙间能流密度10 MW·m-2进行计算,水冷条件取水压4 MPa,流速10 m·s-1,水温350 K[40].为了评估排布位错的直角、斜边瓦片的热性能,首先研究了第一类ELMs 热流作用下两种形状瓦片在存在排布位错时的温度演化.

图4 能流密度随时间变化关系曲线,ELMs 能流密度峰值为 3333 MW·m-2,间隙间能流密度为10 MW·m-2Fig.4.Temporal evolution of energy flux of an ELM with peak heat flux of 3333 MW·m-2 plus an inter-ELM steadystate heat flux of 10 MW·m-2.

3.3 温度分布

3.3.1 直角瓦片

排布误差为0–0.3 mm 的直角瓦片在图1 所示位置1 处的温度随着入射能流密度的增加迅速增加,最先达到熔点温度,源于排布误差为0–0.3 mm的直角瓦片都是在图1 所示位置1 处能流密度最大.瓦片表面各点温度上升的速度不同,其他各点的温度先后也超过了熔点温度,瓦片表面形成了熔化层.随着瓦片表面温度的上升,汽化和热辐射损失的能量也随之增加.但是,只要入射到瓦片表面的能量大于汽化和热辐射损失的能量,瓦片表面的温度会继续升高,当入射能流密度和损失掉的能流密度相等时,表面温度达到最大值.

如图5 所示,排布误差为0 的直角瓦片位置1处在t=0.37 ms 时温度达到最大,最高温度约为9195 K,而此时位置2 处温度为4425 K,在t=0.41 ms 时位置2 处达到最高温度4552 K,各点最高温度晚于能流密度的最大值.图6(a)给出了t=0.37 ms 时瓦片的温度分布,可以看出,从瓦片表面向下,温度迅速减小,仅在瓦片表面形成极薄的一个熔化层,此时位置1 处熔化厚度约为115 μm,位置2 处熔化厚度为20 μm,0.13 ms 后位置1 处熔化厚度达到最大值约128 μm,0.11 ms 后位置2处熔化厚度达到最大值30.1 μm.随着能流密度的逐渐减小,入射能流密度将小于汽化和热辐射损失掉的能流密度,温度开始下降,t=1.0 ms 时,位置1 处温度为3661 K,位置2 处温度为2879 K,表明此时瓦片已经完全凝固.

图5 排布误差为0 的直角瓦片位置1 和位置2 处温度随时间的变化Fig.5.Temporal evolution of temperatures in areas near location 1 and 2 of unshaped tile with no misalignment.

图6 (a) t=0.37 ms 时,排布误差为0 的直角瓦片的温度分布;(b) t=0.29 ms 时,排布误差为0.3 mm 的直角瓦片的温度分布,图中实线为T=3683 K 等温线Fig.6.Temperature distribution of unshaped tile with (a) no misalignment at t=0.37 ms and (b) misalignment of 0.3 mm at t=0.29 ms.Solid line represents an isotherm of 3683 K.

排布误差不同,瓦片缝隙附近的能流密度分布不同,瓦片边缘最高温度不同.排布误差为0.3 mm的直角瓦片位置1 处在t=0.29 ms 时温度达到最大值约9626 K,熔化厚度为93.3 μm,此时位置2的温度约为4693 K,熔化厚度约为5.1 μm,如图6(b)所示.位置1 在t=0.70 ms 时熔化厚度达到最大值139 μm;位置2 处在t=0.4 ms 时温度达到最大值约5342 K,熔化厚度为26.6 μm,0.16 ms后位置2 处的熔化厚度达到最大值约为48.4 μm.排布误差在0–0.3 mm 范围内的直角瓦片,在ELMs过程中冷却管的温度没有变化,说明ELMs 热流对铜中间层和铬锆铜冷却管基本不能造成损伤.

图7 给出了直角瓦片在ELMs 热流作用下最高温度随排布误差的变化规律,排布误差在0–0.3 mm 范围内,直角瓦片的最高温度基本随排布误差线性增加,排布误差越大,直角瓦片的最高温度越高.排布误差从0 增加到0.3 mm,直角瓦片在ELMs 热流作用下的最高温度增加了约4.7%,最大熔化厚度增加了约8.2%.

图7 直角瓦片最高温度随排布误差的变化Fig.7.Highest temperature of unshaped tile versus misalignment.

3.3.2 斜边瓦片

斜边瓦片表面温度随着入射能流密度的增加迅速增加,因为沉积到各点的能流密度不同,瓦片上各点温度上升的速度不同.排布误差为0–0.3 mm斜边瓦片面向入射等离子体棱边区域(图1 中位置3 处),因为相邻瓦片的磁遮挡,能流密度最小,而位置4 处能流密度最大,能流密度对温度有直接决定作用,所以斜边瓦片位置4 处的的温度最高,位置3 处的温度最低.

图8 给出了排布误差为0 的斜边瓦片位置3和位置4 区域温度随时间的变化关系曲线,t=0.38 ms 时位置4 处的温度达到了最高温度,也是斜边瓦片在整个ELMs 过程中的最高温度约为6318 K,位置3 处在t=0.37 ms 时的温度达到最大值约为1072.5 K.在t=1 ms 时,位置4 处的温度为3722 K 略高于钨熔点温度,位置3 处的温度为999.4 K,说明第1 类ELMs 结束时位置4 附近区域依然处于熔化状态,位置3 处始终没有熔化.图9(a)为排布误差为0 的斜边瓦片t=0.38 ms 时的温度分布,此时位置4 处熔化厚度约为55.0 μm,0.24 ms 后该区域熔化厚度达到最大值约为72.5 μm,滞后于温度最高值时刻,这是因为温度开始下降时,沉积在瓦片中的能量会继续向下传导,导致瓦片会继续向下熔化,最终熔化厚度达到最大值.图9(b)给出了排布误差为0.3 mm 的斜边瓦片t=0.38 ms的温度分布,此时位置4 处的温度达到了最高温度约为7251 K,熔化厚度为77.1 μm,位置3 处温度为2046 K,0.23 ms 后位置4 处的熔化厚度达到最大值约为99.6 μm,在整个ELMs 过程中位置3 区域没有熔化.从图9 可以看出发生第1 类ELMs时,斜边瓦片排布误差无论为0 还是0.3 mm,从瓦片表面向下温度迅速减小,ELMs 过程中铬锆铜冷却管和铜中间层温度没有升高,ELMs 热流对钨/铜瓦片的热腐蚀基本局限于钨表面.

图8 排布误差为0 的斜边瓦片位置3 和位置4 处温度随时间的变化Fig.8.Temporal evolution of temperatures in location 3 and 4 of beveled tile with no misalignment.

图9 (a) t=0.38 ms 时,排布误差为0 的斜边瓦片的温度分布;(b) t=0.38 ms 时,排布误差为0.3 mm 的斜边瓦片的温度分布;图中洋红色实线为T=3683 K 等温线Fig.9.Temperature distribution of beveled tile with (a) no misalignment at t=0.38 ms and (b) misalignment of 0.3 mm at t=0.38 ms.Solid line represents an isotherm of 3683 K.

图10 给出了斜边瓦片最高温度随排布误差的变化规律,斜边瓦片最高温度基本随排布误差线性增加,排布误差越大,斜边瓦片最高温度越大.排布误差从0 增大到0.3 mm,斜边瓦片最高温度升高了约14.7%,最大熔化厚度增大了约37.2%.但是,排布误差为0.3 mm 的斜边瓦片对比于直角瓦片最高温度低了约2374 K,最大熔化厚度小了约39 μm.

图10 斜边瓦片最高温度随排布误差的变化Fig.10.Highest temperature of beveled tile versus misalignment.

3.4 侵蚀量

3.3 节研究了不同排布误差下两种形状瓦片温度分布的规律,并分析了原因.为了更好地比较出现排布误差时两种不同形状瓦片的热性能,引入了两个反映瓦片热性能的物理量: 熔化体积比和汽化体积比.

3.4.1 熔化体积比

为了更好地比较不同形状瓦片的热性能,定义了瓦片熔化体积比(每个瓦片的熔化体积与瓦片总体积的比值)这样一个物理量.图11 给出了排布误差(δ)为0 和0.3 mm 两种形状瓦片熔化体积比随时间的变化关系曲线.熔化体积比增大的过程表明瓦片在不断熔化,熔化体积比不断减小时说明瓦片正在凝固.从图11 可以看出无论是哪种形状瓦片,排布误差越大,越早开始熔化,越晚完成凝固.

图11 排布误差为0 和0.3 mm 直角、斜边瓦片熔化体积比随时间的变化Fig.11.Melting volume ratios of unshaped and beveled tiles with misalignment of 0 and 0.3 mm versus time.

图12 给出了两种形状瓦片最大熔化体积比随排布误差的变化关系曲线,排布误差从0 增大到0.3 mm,直角瓦片最大熔化体积比从0.071%增大到0.116%,增加了约63%;斜边瓦片从0.096%增大到0.101%,增加了约5%.排布误差增大时,直角瓦片熔化体积比增加较多,斜边瓦片增加较少,这是因为斜边瓦片面向入射等离子体一侧的棱边会被相邻瓦片磁遮挡,避免了凸出棱边出现,所以斜边瓦片有较强地对抗排布位错的能力.从图12还可以看出,排布误差小于约0.17 mm 时,直角瓦片最大熔化体积比小于斜边瓦片,超过0.17 mm之后直边瓦片最大熔化体积比大于斜边瓦片.对该现象分析如下: 排布误差为0 时,直角瓦片能流密度极大值区域(位置1 区域)面积极小,且瓦片表面能流密度沿着位置1 向瓦片表面中心方向迅速衰减为入射值,而斜边瓦片除位置4 附近区域因瓦片缝隙导致能流密度增大,整个表面的能流密度因为β角的存在变大,所以斜边瓦片熔化体积比较大;随着排布误差增加,直角瓦片位置1 处能流密度大幅度的增加,导致直角瓦片熔化体积比大于斜边瓦片熔化体积比.

图12 直角和斜边瓦片最大熔化体积比随排布误差的变化Fig.12.Maximum melting volume ratios of unshaped and beveled tiles versus misalignment.

3.4.2 汽化体积比

图13 给出了排布误差为0 的直角和斜边瓦片汽化体积比随时间的变化规律,直角、斜边瓦片的汽化体积随着瓦片表面温度的升高而增加,直角瓦片的最大汽化体积比大约是斜边瓦片最大汽化体积比的8 倍,直角瓦片最大汽化厚度约为斜边瓦片最大汽化厚度的53 倍,分别约为3.7 和0.07 μm.

图13 排布误差为0 直角和斜边瓦片汽化体积比随时间的变化Fig.13.Vaporization volume ratios of unshaped and beveled tiles with no misalignment versus time.

图14 给出了的直角和斜边瓦片最大汽化体积比随排布误差的变化规律,排布误差从0 到0.3 mm,直角瓦片的最大汽化体积比增加了约11.7 倍,斜边瓦片的增加了约2.5 倍,在出现排布位错时,直角瓦片比斜边瓦片更易受到影响,汽化量迅速增加.

图14 直角和斜边瓦片最大汽化体积比随排布误差的变化Fig.14.Maximum vaporization volume ratios of unshaped and beveled tiles versus misalignment.

4 讨论

ITER 偏滤器靶板在稳态运行时能承受的最大能流密度预期为10 MW·m-2,慢瞬态事件(是指部分脱靶失控导致刮削层的全部能量打到滤器靶板的现象,持续时间一般为几秒钟)中能承受的最大能流密度为20 MW·m-2[1,40],在两种能流密度作用下,直角和斜边瓦片最高温度随排布误差变化关系曲线如图15 所示.排布误差为0 时,直角、斜边瓦片在10 MW·m-2 能流密度作用下,稳态时温度分别约为1482 和1590 K,在20 MW·m-2 能流密度作用下,稳态时温度分别约为2767 和2993 K,直角瓦片的最高温度分别低于斜边瓦片,随着排布误差的增加,约超过0.105 mm 时,直角瓦片的最高温度高于斜边瓦片,这也是瓦片采用斜边形状的初衷,排布误差为0.3 mm 时,直角瓦片在20 MW·m-2能流密度作用下出现熔化.但是,发生第一类ELMs时,排布误差为0 的直角瓦片最高温度却高于斜边瓦片,其原因分析如下: 虽然直角瓦片迎着等离子体一侧的棱边区域(图1 位置1处)能流密度极大,但是该区域面积极小,使得在稳态和慢瞬态事件的能流作用下,位置1 区域总能流小于斜边瓦片位置4 区域总能流,所以此两种情况下,直角瓦片的最高温度低于斜边瓦片的最高温度.但是,当等离子体能流密度不断增加,导致位置1 区域的总能流大于位置3 区域总能流,最终直角瓦片的最高温度高于斜边瓦片的最高温度.图16给出了排布误差为0 的直角、斜边瓦片最高温度随入射等离子体能流密度变化的规律,可以看出,当入射等离子体能流密度大于约60 MW·m-2时,直角瓦片的最高温度高于斜边瓦片的最高温度.

图15 直角、斜边瓦片最高温度随排布误差的变化,其中入射能流密度为10 和20 MW·m-2Fig.15.Highest temperatures of unshaped and beveled tiles versus misalignment,where the incident heat is 10 and 20 MW·m-2.

图16 直角、斜边瓦片最高温度随能流密度的变化Fig.16.Highest temperatures of unshaped and beveled tiles versus heat flux.

5 结论

本文建立了二维对流传热的自洽模型,详细研究了类ITER ELMs 热流对排布误差为0–0.3 mm偏滤器靶板直角、斜边瓦片的热腐蚀程度.为了保证模拟结果的准确性,利用二维边缘等离子体动理学程序(2d3v PIC-MCC) 研究了瓦片缝隙对等离子体行为的影响,给出了瓦片表面能流密度的分布,并将其作为热传导模型的输入参数.研究结果表明:

1)排布误差为零时,ELMs 间隙间,直角瓦片表面最高温度低于斜边瓦片,ELMs 过程中,直角瓦片最高温度、最大熔化厚度和最大汽化厚度大于斜边瓦片,但是熔化的总体积较小,熔化体积比小于斜边瓦片;

2)随着排布误差增大,瓦片边缘处等离子体能流密度重新分布现象越加明显,直角瓦片面向入射等离子一侧棱边处能流密度迅速增加,斜边瓦片因为相邻瓦片的磁遮挡不会出现凸出棱边,背向入射等离子体一侧的棱边处能流密度随排布误差的增加较缓慢,因此,直角瓦片热侵蚀程度增加速度高于斜边瓦片,在ELMs 间隙间,排布误差超过约0.105 mm 时,直角瓦片的最高温度反超斜边瓦片,ELMs 过程中,排布误差超过0.17 mm 时,直角瓦片最大熔化体积比反超斜边瓦片,说明斜边瓦片具有较强的对抗ELMs 热流和排布位错的能力,出现位错现象时热性能相对比较稳定.ELMs 过程中两种形状瓦片的铬锆铜冷却管和铜中间层温度没有升高,ELMs 热流对排布误差在0–0.3 mm 范围内的钨/铜瓦片的热腐蚀基本局限于钨材料表面.