本征磁性拓扑绝缘体MnBi2Te4 研究进展*
2023-10-06谢向男李成曾俊炜周珅江天
谢向男 李成 曾俊炜 周珅 江天†
1) (国防科技大学理学院,量子信息研究所,长沙 410073)
2) (国防科技大学计算机学院,量子信息研究所兼高性能计算国家重点实验室,长沙 410073)
本征磁性拓扑绝缘体非平庸拓扑态和磁有序的相互作用使其具备量子反常霍尔效应和轴子绝缘体等奇异物理性质,在低功耗拓扑自旋电子器件及拓扑量子计算等方面展现广泛应用前景.自2019 年第一种本征磁性拓扑绝缘体MnBi2Te4 在实验上被发现以来,该材料体系领域迅速吸引了大量研究者的目光,引发了研究热潮.本文将从MnBi2Te4 基本性质出发,介绍近期本征磁性拓扑绝缘体MnBi2Te4 的一些重要研究成果,着重阐述MnBi2Te4 系列的量子反常霍尔效应、轴子绝缘体态和马约拉纳零能模等拓扑量子态,并列举该材料体系其他研究方向及目前存在的问题.最后,总结并展望MnBi2Te4 的下一步研究,期望为相关领域人员的研究提供一定参考价值.
1 引言
回顾拓扑绝缘体(TI)的研究历史,第一代和第二代拓扑绝缘体(TIs)分别是 HgTe/CdTe 量子阱[1,2]和Bi-Sb 合金[3,4],但它们的能带结构复杂,因此理论和实验研究较困难.2009 年,以Bi2Se3为代表的第三代拓扑绝缘体[5]问世,由于其在相干自旋传输[6]、高性能催化[7]和量子信息调控[8]等领域展现的巨大潜力,引发了人们研究的广泛兴趣.此类Z2拓扑绝缘体的拓扑性质受时间反演对称性保护.当其时间反演对称性被长程磁有序破坏时,会形成新的拓扑态(磁性拓扑绝缘体).虽然学术界已经预测、验证很多非磁绝缘体的拓扑相,但磁性材料的拓扑相很少被研究分析.这是因为磁性材料复杂的相互作用使其理论预测更加困难;并且实际磁性材料经常出现各种磁畴和缺陷,纯净磁性材料的制备面临巨大挑战.然而,磁性自由度与空间群结合形成巨大的磁空间群.这极大丰富了磁性拓扑物质态,进而为调控拓扑态提供更多的机遇、为探索各种奇异量子现象提供有效途径.所以磁性拓扑绝缘体在实验上更具吸引力.目前该领域尚处于初步探索阶段.前几年,大量的实验研究多集中在磁性掺杂的TIs[9,10]和磁拓扑异质结[11-14].然而,在磁掺杂TI 薄膜中,磁性杂质的随机分布使得人们只能在超低温度下观测到奇异量子现象.在磁拓扑异质结中,磁性和拓扑性之间的耦合通常较弱,且敏感地依赖于界面性质.这使得磁性导致的拓扑量子态的实验实现较困难.对它们的研究相当有挑战性并且进展缓慢.因此,发现简单、易于控制的本征磁性拓扑绝缘体将对该领域的研究具有重要推动意义.
近年来,第一次被发现的本征磁性拓扑绝缘体MnBi2Te4(MBT)引起了人们的广泛关注.它可以在不同的空间尺寸和磁场调控下表现极其丰富的拓扑量子态,包含奇数层MBT 薄膜的高温量子反常霍尔效应[15-17];偶数层MBT 薄膜的轴子绝缘体态拓扑磁电效应[15,18];在费米能级附近包含一对Weyl 点的理想的Weyl 半金属[15,16];通过与s波超导体[19]相互作用可能存在的马约拉.这种同时具备拓扑性和磁性的本征磁性拓扑绝缘体,不仅为研究拓扑磁有序结构和新颖的拓扑相变提供了理想的平台,而且对低功耗甚至无功耗的拓扑自旋电子器件[20]、太赫兹辐射器件[21]及拓扑量子计算[22]等领域的发展起到积极推动作用,如图1所示.

图1 磁性拓扑绝缘体奇异拓扑性质及应用前景[23] (a) 量子反常霍尔效应[9];(b) 轴子绝缘体态[24,25];(c) 太赫兹辐射[21];(d) 手性马约拉纳费米子及拓扑量子计算[26]Fig.1.Singular topological properties and application prospects of magnetic topological insulators[23]: (a) Quantum anomalous Hall effect[9];(b) axion insulator state with antiparallel magnetization [24,25];(c) terahertz radiation[21];(d) chiral Majorana fermions and topological quantum computation[26].
2010 年,Mong 等[27]曾理论预言存在一种本征的反铁磁拓扑绝缘体,即使不满足时间反演对称性,但当其满足时间反演Θ和空间平移对τ1/2的联合对称性S(S=Θτ1/2)时,可以同时保留磁性和拓扑性.2013 年,韩国科学家[28]最早合成MBT多晶,但并没有涉及拓扑性和磁性的研究.因此,未引起凝聚态相关领域研究者的关注.直到2018年,该领域的研究者才开始关注这一点.由此拉开了MBT 体系中本征磁性拓扑性的研究序幕[15,29,30].
清华大学何珂研究组[29]使用分子束外延方法成功合成MBT 薄膜,观测到典型的Dirac表面态,并指出该体系具有A 型反铁磁结构.这表明该体系是一类新的磁性拓扑绝缘体.南京大学张海军和复旦大学王靖研究组[15]理论上最早指出MBT 体系是受S对称性保护的三维反铁磁轴子绝缘体,其轴子场θ=π;并且验证了其A 型反铁磁结构.清华大学徐勇与合作者[16]通过第一性原理计算独立发现MBT 体系的磁性和拓扑性,特别是预言了奇数层和偶数层MBT 分别对应着量子反常霍尔态和轴子绝缘体态.国际上,西班牙Chulkov团队[30]与国内研究者几乎同时发现了MBT 的磁性和拓扑性.很快地,国内外越来越多的研究组对MBT体系展开了深入系统的研究.
目前,MBT 拓扑量子物态的实验研究已取得突破性进展[31-33].中国研究人员在该材料体系的研究处于世界领先地位.复旦大学张远波和中国科学技术大学陈仙辉研究组[31]实验上证实了MBT具有A 型反铁磁结构且其奈尔温度为25 K,率先在1.4 K 观测到奇数层MBT 手撕薄膜的高温量子反常霍尔效应.清华大学王亚愚和徐勇等[32]发现MBT 薄膜(6 SL)在磁场下可实现量子反常霍尔态与轴子绝缘态之间的量子转变.北京大学王健课题组[33]实现了MBT 器件高陈数的量子反常霍尔态.清华大学王亚愚团队和张金松团队合作[34]测量出只存在于偶数层轴子绝缘态MBT 的非定域电阻.并与华中科技大学脉冲强磁场中心合作,发现陈绝缘体态(或者说量子反常霍尔态).MBT在高达61 T 的超强磁场下存在一个以零级霍尔平台和螺旋式边缘态输运为典型特征的新拓扑物态[35].中国科学研究院田明亮课题组[36]证实了在大于10 T 磁场下MBT 由于轨道磁矩存在平面霍尔效应等.此外,国际上,哈佛大学的Xu Su-Yang与加州大学洛杉矶分校倪霓[37]合作发现偶数层MBT 在电场作用下产生层霍尔效应,有助于表征其轴子绝缘态.加州大学洛杉矶分校Wang 研究组[38]发现了磁性拓扑绝缘体MBT 极性可调的反常霍尔效应.新加坡南洋理工大学的王骁及其合作者研究组[39]和Zhang 等[40]分别在MBT/Pt 和MBT 样品中观测到非互易效应.清华大学杨鲁懿研究组[41]揭示了原子薄层MBT 的层间范德瓦耳斯耦合强度及其超快光学性质.这些突破性结果为低功耗的新型纳米拓扑自旋电子器件的开发应用提供了全新思路.
本文将总结归纳MBT 的基本性质、奇异的拓扑量子态、该材料体系其他的研究方向及存在的问题,并对其下一步的研究做出展望.
2 MBT 基本性质
2.1 晶体结构
MBT 是一种A-B-C 型密堆型范德瓦耳斯层状结构材料.Te-Bi-Te-Mn-Te-Bi-Te 七原子层(septuple layer,SL)是其基本单元;Mn 原子层位于每个SL 单元的中心.MBT 的每个SL 层可以看作一个五原子层Bi2Te3中间插入一个额外的Mn-Te双分子层.SL 单元内部,近邻原子之间形成强共价键,而SL 单元之间是弱的范德瓦耳斯相互作用.该体系空间对称性与Bi2Te3的一致,属于空间群(No.166),晶格常数a=b=4.36 Å和c=40.6 Å[42-44],如图2(a)所示.清华大学何珂柯研究组[29]使用高分辨扫描透射电子显微镜(STEM)对MBT 薄膜(5 SLs)实空间的晶体结构进行了表征.高角度环形暗场(HAADF)图像清楚地显示其特征SL 结构,如图2(b)所示.图2(c)显示沿两个SLs 的原子剖面强度分布图(cut 1).在SL 中不同位置的原子对比度变化很大.HAADF-STEM 图像中原子的对比度与其原子序数直接相关.因此,沿SL 的强度分布与Te-Bi-Te-Mn-Te-Bi-Te 原子排列相一致.X 射线衍射(XRD)表征MBT 薄膜的面外晶体结构并证实其高质量晶体结构.在Si(111)衬底上生长的MBT 薄膜沿着 (00l)晶面,如图2(d)所示.
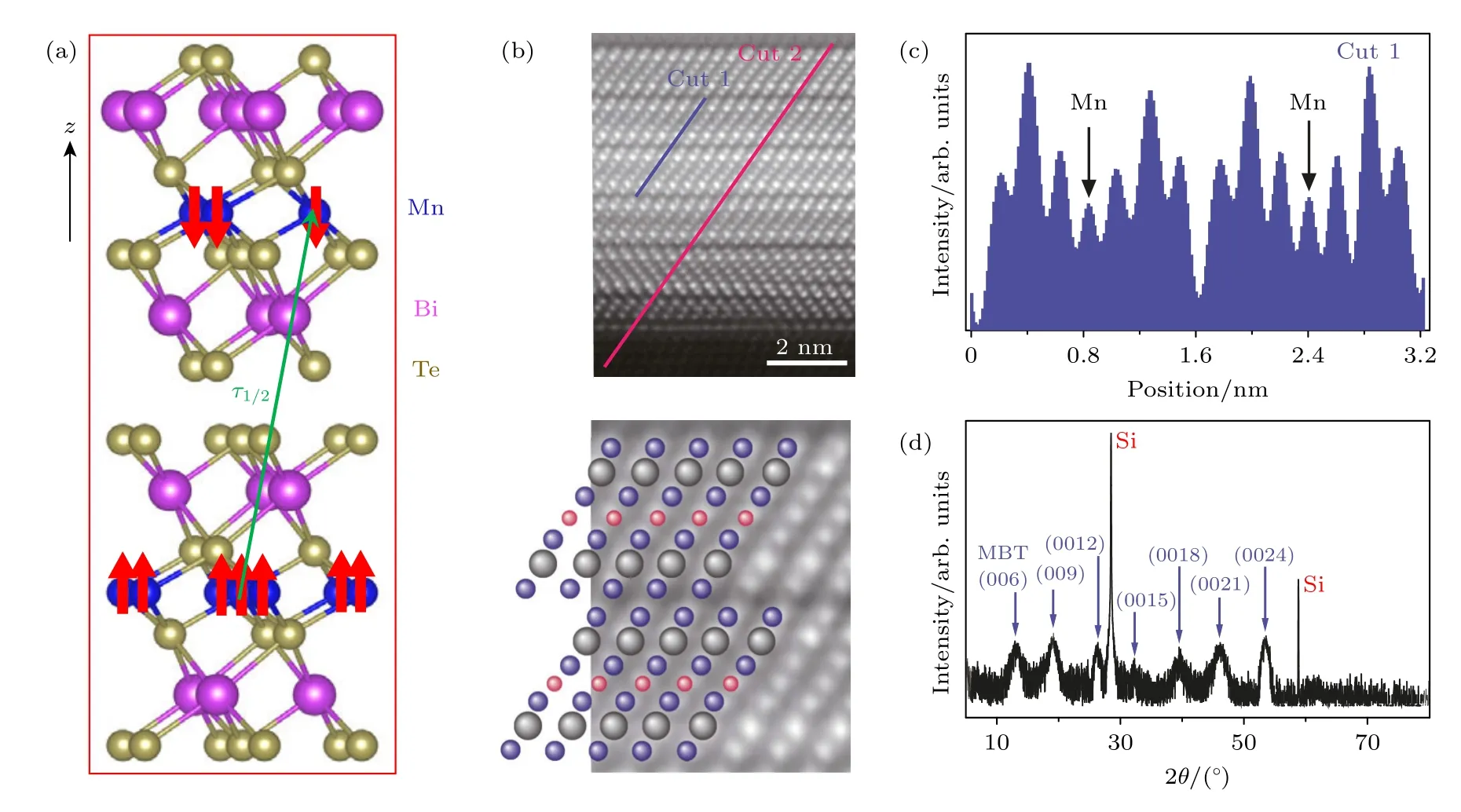
图2 MBT 的晶体结构图[15,29] (a) 由两个SLs 组成反铁磁MBT 的原子结构图[15].每个SL 内为铁磁性,相邻SL 之间为反铁磁性.红色箭头表示Mn 原子磁矩;绿色箭头表示空间平移算符τ1/2;(b) 在Si(111)衬底上生长的5 SLs MBT 薄膜的横截面HAADF-STEM图像[29];(c) HAADF-STEM 沿(b)中Cut 1 的强度分布图[29];(d)在Si(111)上生长的MBT 薄膜的XRD 图[29]Fig.2.Crystal structure in MBT[15,29]: (a) Atomic structure of MBT consists of two SLs,whose magnetic states are ferromagnetic within each SL and antiferromagnetic between adjacent SLs[15].The red arrows represent the spin moment of Mn atom.The green arrow denotes for the half translation operator τ1/2;(b) cross-sectional HAADF-STEM image of a 5 SLs MBT films grown on a Si(111) substrate[29];(c) intensity distribution of HAADF-STEM along Cut 1 in panel (b)[29];(d) XRD pattern of MBT films grown on Si(111)[29].
2.2 磁性
MBT 的磁性主要由Mn 的3d 态提供.理论计算表明,MBT 是一种具有范德瓦耳斯层状结构的本征反铁磁拓扑绝缘体AFM TI,在SLs 内保持铁磁(FM)有序,在相邻SLs 之间保持反铁磁(AFM)有序[15,17,30].每层SL 中的单个Mn2+离子预计贡献5µB磁矩.在磁基态下,Mn 原子的磁矩沿着面外易轴z方向,相邻SL 层之间的磁矩相反,因此具有A 型AFM-z磁基态,如图2(a)所示.在MBT中,Mn 原子位于由相邻Te 原子形成的轻微畸变八面体的中心,Mn-Te-Mn 超交换作用引起的层内FM 耦合明显强于Mn-Te···Te-Mn 超交换作用导致的层间AFM 耦合[29].利用非弹性中子散射证实了长程FM 层内耦合、AFM 层间耦合和面外易轴z的磁各向异性[45,46].北京大学叶堉及其合作者[47]使用反射式磁圆二向色谱(RMCD)首次研究了从单层到少层的MBT 在层数、温度和外磁场等参数变化下的磁行为.通过对RMCD 信号的温度拟合,得到层数-温度磁相图,如图3(a)所示.随着温度升高,MBT 经历反铁磁到顺磁的磁相变;并且随着层数的增加,奈尔温度TN逐渐升高直至达到体态的24.5 K.他们认为随着样品趋近二维(2D)极限,热扰动增加,进而抑制TN.在TN以下,利用平均场近似模拟得到各个不同层厚样品随温度、外磁场下的磁相变演化,从而获得在各个层厚下样品的磁场-温度磁相图,如图3(c)和图3(d)所示.图中展示了2 SLs 和3 SLs MBT 的磁场-温度磁相图.理论计算的A-AFM 与CAFM 相转变的临界spin-flop 场µ0H1值和CAFM 与FM 相转变的临界spin-flip 场µ0H2值与实验测得的结果一致.这种一致性有望进一步揭示MBT 体系中磁性和拓扑性的相互关系,并且利用层数、外场等调控磁性从而调控拓扑性成为可能.随后,新加坡南洋理工的王骁与其合作者[39]实验上在12 SLs层MBT 中也得到了类似的磁场-温度磁相图,如图3(b)所示.

图3 MBT 磁相图 (a) MBT 薄膜的层数-温度相图[47];PM 代表顺磁区域;A-type AFM 代表A 型反铁磁区域;(b) 12 SLs MBT/Pt异质结自旋排列随温度和外加磁场的变化[39];(c) 2 SLs MBT 的温度-磁场相图[47];(d) 3 SLs MBT 的温度-磁场相图[47];白色圆圈和三角形分别表示在不同温度下计算得到的spin-flop 场μ0H1 和spin-flip 场μ0H2,即A-AFM/CAFM 相和CAFM/FM 相的临界转变点;实验数据点用灰色的球和三角形表示Fig.3.Magnetic phase diagram of MBT: (a) Layer number-temperature phase diagram of the MBT flake[47];PM denotes the region where the flake is paramagnetic;A-type AFM denotes the region where adjacent ferromagnetic SLs couple antiferromagnetically with each other;(b) spin configuration of 12 SLs MBT/Pt bilayer as functions of temperature and external magnetic field[39];(c) temperature-field phase diagram of 2 SLs MBT[47];(d) temperature-field phase diagram of 3 SLs MBT[47];the white circles and triangles represent the calculated spin-flop field μ0H1 and spin-flip field μ0H2,respectively,at various temperatures,showing the boundaries of the A-type AFM/CAFM phase and CAFM/FM phase;the experimental data points are represented using grey spheres and triangles with corresponding error bars.
2.3 拓扑性
磁性体系不具有时间反演对称性Θ,而拓扑绝缘体的拓扑性是受时间反演对称性保护的.在磁性拓扑绝缘体中,当Θ被有磁序打破时,它与某些磁晶格对称性(如旋转对称性Cn和平移对称性τ1/2等)结合组成的联合对称性等效于Θ,使得系统仍然保持拓扑性[15,23].2010 年,Mong 等[27]理论预言存在一种三维本征的反铁磁拓扑绝缘体3D AFM TI,即使不满足时间反演对称性,但当其满足时间反演对称操作Θ和空间平移操作τ1/2的联合对称性S时,可以同时保留磁性和拓扑性.与3D TI 不同的是,3D AFM TI 只在某些S对称性破缺的表面上具有无带隙的拓扑表面态;而3D TI 所有表面都具有Θ保护的无带隙的拓扑表面态.直到2018 年,实验上第一个被发现的本征反铁磁拓扑绝缘体MBT 单晶的成功合成[29]验证了上述的理论预测,并引发了人们对本征磁性拓扑绝缘体的研究热潮.MBT 具有弱拓扑性,拓扑非平庸性主要由Bi 元素和Te 的p 态提供.其表面态不再像3D TI 那样全部表面保持无带隙,而是在满足S对称性的表面上才保持无带隙[42].例如,在保持S对称性的(011)面,MBT 存在无带隙的拓扑表面态;而在S对称性破缺的(001)和(111)晶面,MBT 拓扑表面态打开带隙,如图4 所示.
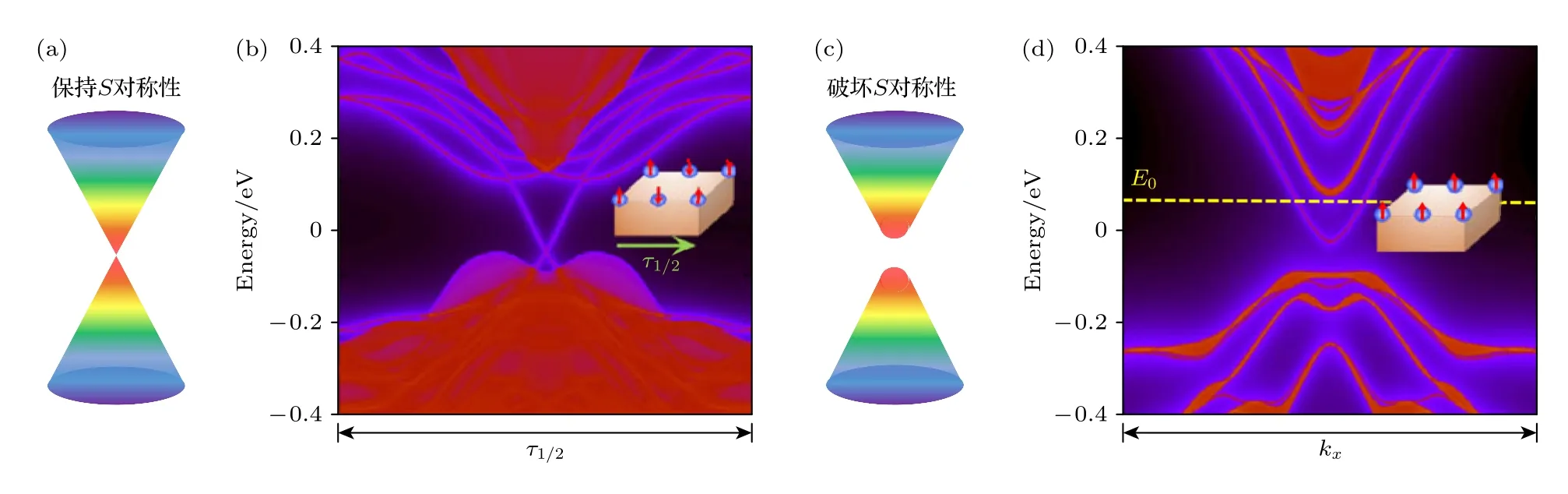
图4 MBT 表面态能带结构图 (a) 保留S 对称性的表面具有无能隙的Dirac 锥表面态示意图[42];(b) MBT(011)方向表面 (保持S 对称性)的表面态[15,42];(c) 破坏S 对称性的表面具有有能隙的Dirac 锥表面态[42];(d) MBT (111)方向表面(破坏S 对称性)的表面态[15,42]Fig.4.Energy band structure of MBT with surface state: (a) The Dirac surface state is gapless due to the S symmetry[42];(b) the surface state on MBT(011) with S symmetry[15,42];(c) the Dirac surface state is fully gapped due to the S symmetry broken[42];(d) the surface state on MBT(111) without S symmetry[15,42].
该材料体系具有丰富的拓扑量子态[16,48].能带结构计算表明[16],MBT 可能出现各种奇异的拓扑相,包括量子反常霍尔绝缘态QAHE、轴子绝缘态AI、量子自旋霍尔绝缘态QSHE、Weyl 半金属WSM、Dirac 半金属DSM 和反铁磁拓扑绝缘态AFM TI,如图5(a)所示.通过空间维度和磁排列调控可改变这些2D 或3D 拓扑量子态.MBT 具有层间反铁磁AFM;根据层数的奇偶性,少层MBT 的上下表面具有相同或相反的磁矩,从而决定了其拓扑性.因此少层MBT 的磁性和相应的拓扑性会随着层数的变化而变化.理论计算[17]表明单层的MBT是拓扑平庸的;偶数层的MBT 是完全反铁磁的,净磁矩为零;三层及三层以上奇数层是非补偿反铁磁的,净磁矩为非零.奇数层的MBT 为C=1 的陈绝缘体态;偶数层的MBT 的C=0,但拓扑上是非平庸的,即为轴子绝缘体态.由于MBT 的层间AFM 相互作用较弱,通过施加适度的面外磁场,MBT 的层间反铁磁序可以调制为面外FM-z,拓扑性质也随之发生变化,成为只有一对Weyl 点的最简单的Ⅱ型磁性WSM.当外部磁场旋转时,系统从FM-z相连续变化到FM-x相;同时,系统由Ⅱ型磁性WSM 相变为Ⅰ型磁性WSM 直至普通FM 绝缘体[49].在无磁场情况下,体态MBT 是一种AFM TI,侧表面态无带隙,而顶部和底部表面态存在磁带隙.对于MBT 薄膜,有带隙的顶部和底部表面态具有相反或相同符号的半整数量子霍尔电导,导致C=0 或 1.C>1 的陈绝缘体态在此薄膜上是不可能存在的.然而,在适度磁场下,块状MBT 变为铁磁 Weyl 半金属.当薄膜厚度处于量子限域区时,铁磁MBT 表现出陈绝缘态;随着薄膜厚度增加,带隙减小,陈数C增大.这种不寻常的特性归因于量子限域效应与MBT 铁磁相的Weyl 半金属特性的结合,为实现高陈数陈绝缘态铺平了道路,如图5(b)所示.
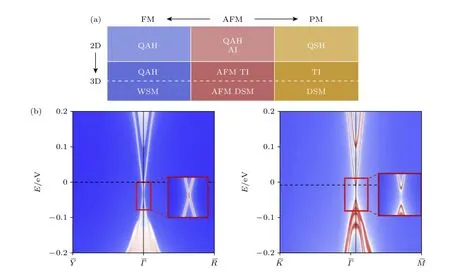
图5 MBT 丰富的拓扑量子态 (a) MBT 薄膜(2D)和块体(3D)在不同磁化状态下丰富的拓扑量子态.QAH,量子反常霍尔态;AI,轴子绝缘体;QSH,量子自旋霍尔态;TI,拓扑绝缘体;WSM,Weyl 半金属;DSM,Dirac 半金属[16,48].(b) MBT (110)面和 (111)面的无带隙和有带隙表面态能带结构[16,48]Fig.5.Rich MBT topological quantum states.(a) MBT thin films (2D) and bulk (3D) have rich topological quantum states in different magnetic states.QAH,quantum anomalous Hall state;AI,axion insulator;QSH,quantum spin Hall state;TI,topological insulator;WSM,Weyl semimetal;DSM,Dirac semimetal[16,48].(b) Surface states of the MBT (110) and (111) surfaces,which are gapless and gapped,respectively[16,48].
接下来,我们将重点介绍MBT 几种代表性拓扑量子态,包括量子反常霍尔态、轴子绝缘体态和马约拉纳准粒子态.
3 MBT 拓扑量子态
3.1 量子反常霍尔态和量子霍尔态
量子反常霍尔效应是一种无需外加磁场而由自发磁化强度引起的量子霍尔效应.拓扑绝缘体的拓扑性受时间反演对称性保护,即存在无带隙的Dirac 锥表面态.当引入磁性后,长程磁有序打破时间反演对称性,并在无带隙的Dirac 锥表面态中引入磁带隙.具有磁带隙表面态的有效哈密顿量表示为:H(k)=(σxky-σykx)+mzσz,其中σ为泡利矩阵,σz=±1 分别代表自旋向上和自旋向下,mz为表面交换场.磁带隙的打开伴随着手性边缘态的出现.当费米能级处于磁带隙中时,量子反常霍尔效应出现,如图6(a)所示.相较于磁性掺杂的拓扑绝缘体和铁磁/拓扑绝缘体异质结而言,在本征磁性拓扑绝缘体中观测QAHE 更具优势,例如其磁性离子的均匀分布、磁性和拓扑性的强耦合有望在更高温度下观察到QAHE 等.在本征磁性拓扑绝缘体MBT 中,厚度大于1 SL 的样品顶部和底部表面态间的杂化可以忽略不计.因此,其拓扑电子性质由上下两个孤立的表面决定.奇数层(偶数层) SLs 的MBT 上下表面具有相同(相反)的mz,既具有相同(相反)的半整数量子化霍尔电导e2/(2h),如图6(b) (图8(a))所示.所以,奇数SL层MBT 薄膜是陈数C=1 的本征量子反常霍尔绝缘体;偶数SL 层薄膜是本征轴子绝缘体(C=0),在直流测量中表现为普通绝缘体,但在交流测量中表现出拓扑磁电效应[18].复旦大学张远波及其合作者[31]在1.4 K 的5 SLs MBT 样品中观察到零场量子反常霍尔效应,即在零磁场下,几乎量子化的霍尔电阻Ryx=0.97(h/e2) 和纵向电阻Rxx=0.061(h/e2)(如图6(c)).外加的7.6 T 磁场促使所有SL 层铁磁排列,进而将量子化温度提高到6.5 K.此外,在5 SLs的薄片中研究门电压调控QAHE时,外加10T 以上的面外磁场、门电压Vg在-20–-60V的情况下,Ryx趋近-h/(2e2)平台,即填充因子v=-2;同时Rxx趋于0,如图7(a)所示.这意味着除了QAH 态之外出现了一个额外的量子霍尔态.他们进一步证实这个额外的量子霍尔态起源于朗道能级.朗道能级与QAH态共存促使Ryx=-h/(2e2).朗道能级量子化只负责两个边缘通道中的一个,QAH 效应贡献另一个边缘通道,如图7(b)所示.北京大学王健及其合作者[33]在9SLs和10SLs的MBT中,外加6–10T的面外磁场时,同样观察到Ryx=h/(2e2)及纵向电阻Rxx的消失,如图7(c)所示.然而研究表明此时v=2 只起源于高陈数C=2,而与朗道能级无关.在6–10 T 的面外磁场范围内,本征AFM TI 的MBT转变为铁磁Weyl 半金属.理论计算表明,由于量子限域效应,铁磁Weyl 半金属MBT 可以实现高陈数绝缘体态,如图7(d)、图7(e)和图7(f)所示.因此,上述观察到的实验现象和理论计算结果相一致.此外,研究者在MBT 异质结中也发现了QAHE[50-52].最近,Ying 等[53]在5 SLs 器件中再现了陈绝缘态,并通过非局域输运测量证实了边缘态的手性.
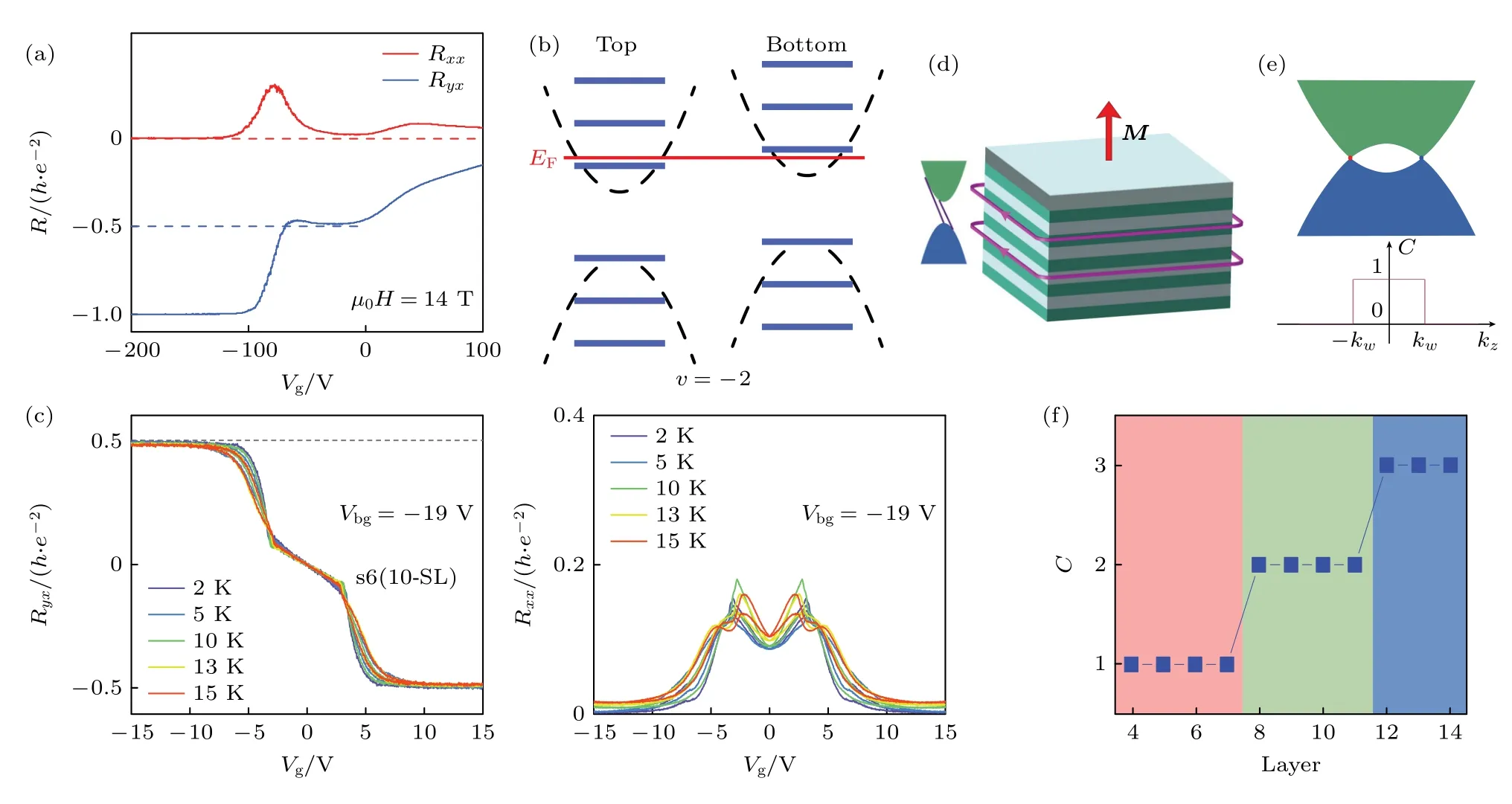
图7 MBT 高陈数陈绝缘体态 (a) 5 SLs MBT 门电压调控的反常霍尔效应[31];(b) 5 SLs MBT 的顶部和底部表面态的示意图[31];(c) 10 SLs MBT 中C=2 的高陈数陈绝缘体态的Ryx 和Rxx 与磁场和温度间的关系[33];(d) 具有两个手性边缘态的高陈数陈绝缘态示意图;灰色和绿色表示相邻SLs 的MBT[33];(e) 铁磁 MBT 能带结构示意图,其为磁性Weyl 半金属[33];(f) 计算得到的MBT陈数随膜厚的变化函数[33]Fig.7.High Chern number of Chern insulator MBT.(a) Anomalous Hall effect of 5 SLs MBT by gate voltage[31].(b) Schematic band diagrams for the top and bottom surface states of this fivelayer sample[31].(c) Temperature and magnetic field dependence of Ryx and Rxx in high-Chern-number Chern insulator states with C=2 in 10 SLs MBT device[33].(d) Schematic of high-Chern-number Chern insulator states with two chiral edge states across the band gap;gray and green indicate adjacent MBT SLs[33].(e) Schematic diagram of band structure of the ferromagnetic MBT,which is a magnetic Weyl semimetal[33].(f) Chern number as a function of film thickness in MBT[33].
3.2 轴子绝缘体态
轴子绝缘体态[48]是一种独特的拓扑相,其陈数C=0,但Chern-Simon 项有限[18].如上所述,偶数SL 层MBT 薄膜是本征轴子绝缘体,在直流测量中表现为普通绝缘体,但在交流测量中表现出拓扑磁电效应[18];与普通绝缘体相比,轴子绝缘体态对有质量的Dirac 表面态具有独特的电磁响应,从而产生半整数量子化表面霍尔电导、量子化拓扑磁电效应和拓扑磁光效应等[54-57].在实验上,轴子绝缘体表现出巨大的纵向电阻和零霍尔电导(或零霍尔电阻),这是由于上下表面霍尔电导相互抵消,如图8(a)所示.然而,普通绝缘体也会表现出这种性质.因此,依据零霍尔电导间接判断轴子绝缘体态的存在显得不充分.所以探索直接判定轴子绝缘体态存在的实验判据尤为重要.接下来,简单介绍几种直接判断轴子绝缘体态存在的证据.
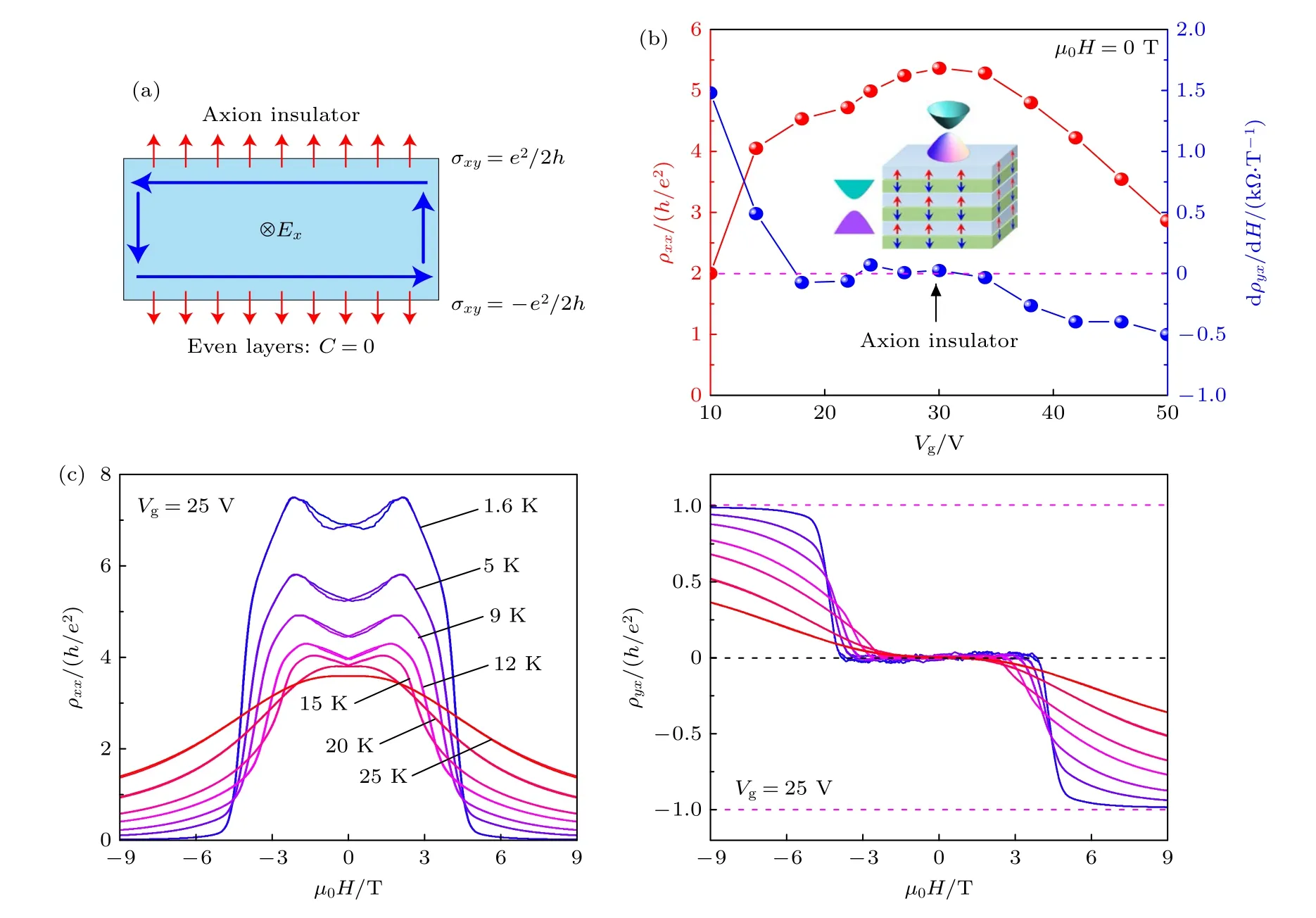
图 8 MBT 轴子绝缘体态[16,32] (a) 偶数层MBT 本征轴子绝缘体的示意图[16].顶部和底部有带隙的表面具有半整数量子化的霍尔电导,其符号在偶数层中相反,导致C=0;(b) 轴子绝缘态的ρxx 和 与栅极电压的依赖关系[32];(c) 栅极电压Vg=25 V时,不同温度下纵向电阻率和霍尔电阻率随磁场强度的变化关系[32]Fig.8.Axion insulator state in MBT[16,32]:(a) Illustration of intrinsic axion insulators in even layers[16].The intrinsically gapped surfaces on the top and bottom sides have half-quantized Hall conductances,whose signs are opposite in even layers,leading to C=0 ;(b) gate dependence of ρxx and in axion insulator state[32];(c) longitudinal and Hall resistivities versus magnetic field strength at various temperatures with gate voltage Vg=25 V[32].
在量子色动力学下,轴子场在麦克斯韦方程中引入了耦合电场和磁场的附加项.根据有效拓扑场论,三维TI 的电磁响应包含附加项[18,58].这类似于拥有附加轴子项的麦克斯韦方程.这里,E和B分别是电场和磁场,h为普朗克常数,θ为轴子角.附加的轴子项耦合磁场和电场,并导致拓扑磁电效应(TME)[15],即电场可以诱导磁极化,而磁场可以诱导电极化.从三维TI 的有效作用量来看,电流项为,其中第1 项jfree为自由电荷电流密度;第2 项是霍尔电流(垂直于电场),完全是由轴子项引起的.这是系统的非平庸拓扑性的结果.如果表面的能隙完全打开,并且体态轴子角完全量化为π,那么轴子项将是稳定系统的唯一电流贡献项.沿着表面法线方向积分,可以得到由每个表面贡献的半整数量子霍尔电导σxy=e2/(2h),其中符号由表面磁矩的方向决定.当磁矩的方向在上下表面相反时,轴子项引起的电流方向相反.因此,虽然某一表面具有半整数霍尔电导,但由于上下表面相互抵消,系统的净霍尔电流变为零,所以可以观察到零平台量子反常霍尔效应ZPQAH.此外,当施加电场时,环形霍尔电流形成.这样的环形霍尔电流相当于表面量子化磁化强度导致的表面磁电流,其中n为整数,c为光速.同样地,施加磁场也能导致电极化.当磁场缓慢增加时,感应电场产生平行于磁场的霍尔电流,电荷在上下表面聚集,相当于量子化极化.这种电场和磁场之间的感应被称为TME,是轴子绝缘体态的直接证据.然而,由于仪器精度和样品质量的严格要求,TME的观测具有很大的挑战性.因此,迄今为止的研究工作一直以探测零霍尔平台作为轴子绝缘体相的证据[12,32].此外,最近提出的二维无序导致的金属-绝缘体转变[55]和层霍尔效应[37]也是判定轴子绝缘体态的间接证据.
实现轴子绝缘态需满足3 个条件[15,18]: 1) 系统的所有拓扑表面态需完全打开带隙;2) 轴子角θ必须有一定的对称性才能量子化;3) 费米面需落入体态和所有表面态的带隙.MBT 作为一种本征磁性拓扑绝缘体,有望克服这些困难.MBT 的磁有序结构使其更有利于避免带隙波动和超顺磁性[15]等无序效应.大带隙有利于在高温下观测轴子绝缘态.偶数层MBT 薄膜的AFM-z相是本征轴子绝缘体,因为其上、下表面态被相反方向的磁矩自然地打开了带隙.清华大学王亚愚与其合作者等[32]报道了6 SLs 的MBT 在 22V ≤Vg≤30 V 栅压范围内,弱磁场下的纵向电阻率较大:ρxx>4.5h/e2;同时在 -3.5T<µ0H<3.5T 磁场范围内霍尔效应保持为零,形成一个较宽的ρyx=0 平台.这是轴子绝缘体的标志特征,它被预测为具有偶数SLs 的MBT 在AFM 态的本征基态[15-17].他们进一步在1.6 K 温度下总结零磁场下ρxx,ρyx与栅压Vg的关系.图8(b)显示零磁场下,当EF被调节到表面态带隙中时 (22 V ≤Vg≤34 V) ,纵向电阻率ρxx表现出很强的绝缘性;同时霍尔效应形成ρyx=0 的平台,因此霍尔电阻率的斜率表现出零平台.这与传统绝缘体不同.他们还研究了栅压Vg为25 V 时,ρxx,ρyx随温度的演化现象,如图8(c)所示.在T=1.6 K 时,弱磁场下MBT 较大的纵向电阻率和较宽的零霍尔平台验证了轴子绝缘态的出现.零磁场中稳固的轴子绝缘态显著提高了发现量子化拓扑磁电和磁光效应以及探索凝聚态系统中的轴子电动力学的可能性[58-61].
3.3 MBT 超导异质结产生马约拉纳准粒子
二十多年来,凝聚态体系中马约拉纳准粒子的实现,包括马约拉纳零能模(MZM)和马约拉纳手性边缘态,一直备受关注[26,62-67].马约拉纳准粒子的主要特征是其反粒子等于它自身,即γ=γ†.理论发现,无自旋一维p 波拓扑超导体[68,69]的边界处和无自旋二维p+ip 拓扑超导体[70-75]的涡旋中心存在零能的MZM,如图9(a)、图9(b)和图9(c)所示.相应地,实验上有望在一维SOC 纳米线[76]、二维异质结[66,77]以及本征材料[78-81]中获得MZM.验证MZM 存在的间接证据有零偏压电导峰[82-85]和整数化分布的能级[79]等.MZM 可以用来构造非局域拓扑量子比特,有望解决量子态易受环境影响产生的退相干问题,并且会带来基态简并度和非局域性[86],因此在拓扑量子计算中有重要的应用[65,86].除了MZM,一维马约拉纳手性边缘态是二维p +ip 手性超导体的拓扑边缘态.Fu 和Kane[66]提出了由铁磁体、TIs 和s 波超导体组成的异质结构,以形成等效的p+ip 超导体,进而获得可能的1D马约拉纳手性边缘态.此外,很多研究组提出,临近s 波超导体的QAHI[64,87-89]、半平台表面QAHI(HPSQAH)[90]和零平台QAHI(ZPQAH)[17,91],可实现马约拉纳手性边缘态.不仅如此,近期研究[92,93]发现,临近超导体的AI 同样可以实现马约拉纳边缘态.Yan 等[92]证明了C=1/2 轴子态对应于马约拉纳基中Chern 数为N=1 的拓扑态.在临近s波超导体,临界超导配对尺度下发生从N=1 向N=0 相的拓扑相变.他们理论分析表明,在AI表面N=1 和N=0 区域的边界处出现了手性马约拉纳铰链模.Zhang 和Liu[93]基于紧束缚模型分析也发现临近超导体的AI 可实现马约拉纳边缘态.与磁掺杂拓扑绝缘体/s 波超导体异质结相比,最近发现的本征磁拓扑MBT 材料家族具有更大的磁交换带隙和更少的无序,并且奇数层为QAHI、偶数层为AI,被认为与s 波超导体组成的异质结是实现手性马约拉纳模的潜在平台.Peng 和Xu[19]提出了利用MBT 和s 波超导体组成的异质结构实现手性马约拉纳态.在这种异质结构中,超导邻近效应可以在MBT 侧表面打开超导间隙.该超导能隙与上下表面的磁交换能隙在拓扑上是截然不同的.在具有这两种能隙表面的共用边,即异质结的铰链,会呈现一维马约拉纳手性边缘态,如图9(d)所示.最近,Chen 等[94]提出,当MBT 薄膜与其上表面的s 波超导体耦合时,无论门电压如何调控,MBT 上表面态的磁能隙始终处于费米能级以下.若调控下表面费米能级到磁带隙中,则会出现手性马约拉纳模,如图9(e)所示.Zhang 和Liu[93]使用第一性原理方法预测在超导衬底上生长的MBT/Bi2Te3薄膜是在较宽能量范围(约80 meV)内实现马约拉纳手性边缘态的理想实验平台.
4 该体系其他研究方向
4.1 MnBi2Te4 异质结及超晶格 [MnBi2Te4(Bi2Te3)n 和MnBi2Te4(MnTe)m]
除MnBi2Te4之外,MnBi2Te4(Bi2Te3)n(n=1,2,3,···) 范德瓦耳斯家族材料也具有本征磁性拓扑性[95,97-107].MnBi2Te4(Bi2Te3)n族的非平庸拓扑结构与该系列中相应的磁性能紧密相连,从而可通过调节层间AFM 耦合强度来调控拓扑态.这一特性有助于在MnBi2Te4家族/拓扑超导体异质结实现马约拉纳准粒子[19].MnBi2Te4家族为探索新的量子拓扑相[31-33],低功耗电子学、自旋电子学[62,108]和拓扑量子计算[65]等领域的应用提供一个可行且高度可调的二维平台.在该体系材料中,MBT 层由n层Bi2Te3隔开,如图10(a)所示.层间AFM相互作用随着MnBi2Te4层间距离的增加而迅速减弱,因此其磁性和拓扑性可以由Bi2Te3层数n大幅度调控.n越大,AFM 耦合越弱,奈尔温度越低,越易形成铁磁基态[109].当n=1 或 2 时,MnBi4Te7和MnBi6Te10分别在奈尔温度为13 K 和11 K时保持层间AFM 耦合[105,106];并且天然超晶格MnBi2Te4(Bi2Te3)n(n=1 和2)[110]存在铁磁及反铁磁相共存和交换偏置效应.理论计算表明,通过材料设计,改变MnBi2Te4和Bi2Te3层的比例及堆叠情况,可以实现多种二维拓扑相,包括时间反演对称的量子自旋霍尔效应、时间反演破缺的量子自旋霍尔效应以及量子反常霍尔效应,如图11(a)所示;并且Mn-Bi-Te 体系随层间电子耦合及交换相互作用的不同展现出丰富的三维拓扑物相,如图11(b)所示.扫描隧道显微镜STM 和角分辨光电子能谱ARPES 实验[111]表明,MnBi4Te7顶部和底部表面态与MnBi2Te4或Bi2Te3截止面相关,存在两种拓扑表面态.这两种表面态强烈依赖表面MnBi2Te4层和Bi2Te3层之间的相互作用.拥有MnBi2Te4截止面的比拥有Bi2Te3截止面的MnBi4Te7顶表面态的能隙小得多[106].MnBi6Te10的侧表面无带隙,顶和底表面态有带隙[97]等.此外,Bi2Te3/ MnBi2Te4异质结[112]的拓扑表面态存在明显磁带隙;MnBi2Te4/Bi2Te3超晶格[50]拥有高温量子反常霍尔态.当n=3 时,输运结果表明,MnBi8Te13在10.5 K 以下进入铁磁相,第一性原理计算和ARPES 测量进一步证明,MnBi8Te13是Z4=2 的本征铁磁轴子绝缘体[98].研究表明[113]拥有MnBi2Te4截止面的MnBi8Te13具有磁性起源的表面态带隙;此带隙随温度的升高而减小,并在顺磁相时完全关闭.另一方面,具有Bi2Te3截止面的MnBi8Te13表面由于铁磁性的缺失,具有无带隙的Dirac 锥表面态.当Bi2Te3层数n进一步增加时,相邻MnBi2Te4SLs 之间的层间交换相互作用变得过于微弱.在临界温度以下,MnBi2Te4SLs被认为是相互磁独立的,并且SLs 的磁化在z轴上变得无序.最近,上海科技大学的寇煦丰和杨雨梦合作[96]报道了具有可调谐磁交换相互作用的铁磁体插层MnBi2Te4超晶格,将铁磁MnTe 层插入MnBi2Te4中,形 成[(MnBi2Te4)(MnTe)m]N超 晶格,如图10(b)所示,并利用偏振中子反射仪和磁电阻测量研究它们的磁相互作用.铁磁体MnTe的加入通过MnBi2Te4/MnTe 异质界面的交换弹簧效应调节了MnBi2Te4层的磁层间耦合.
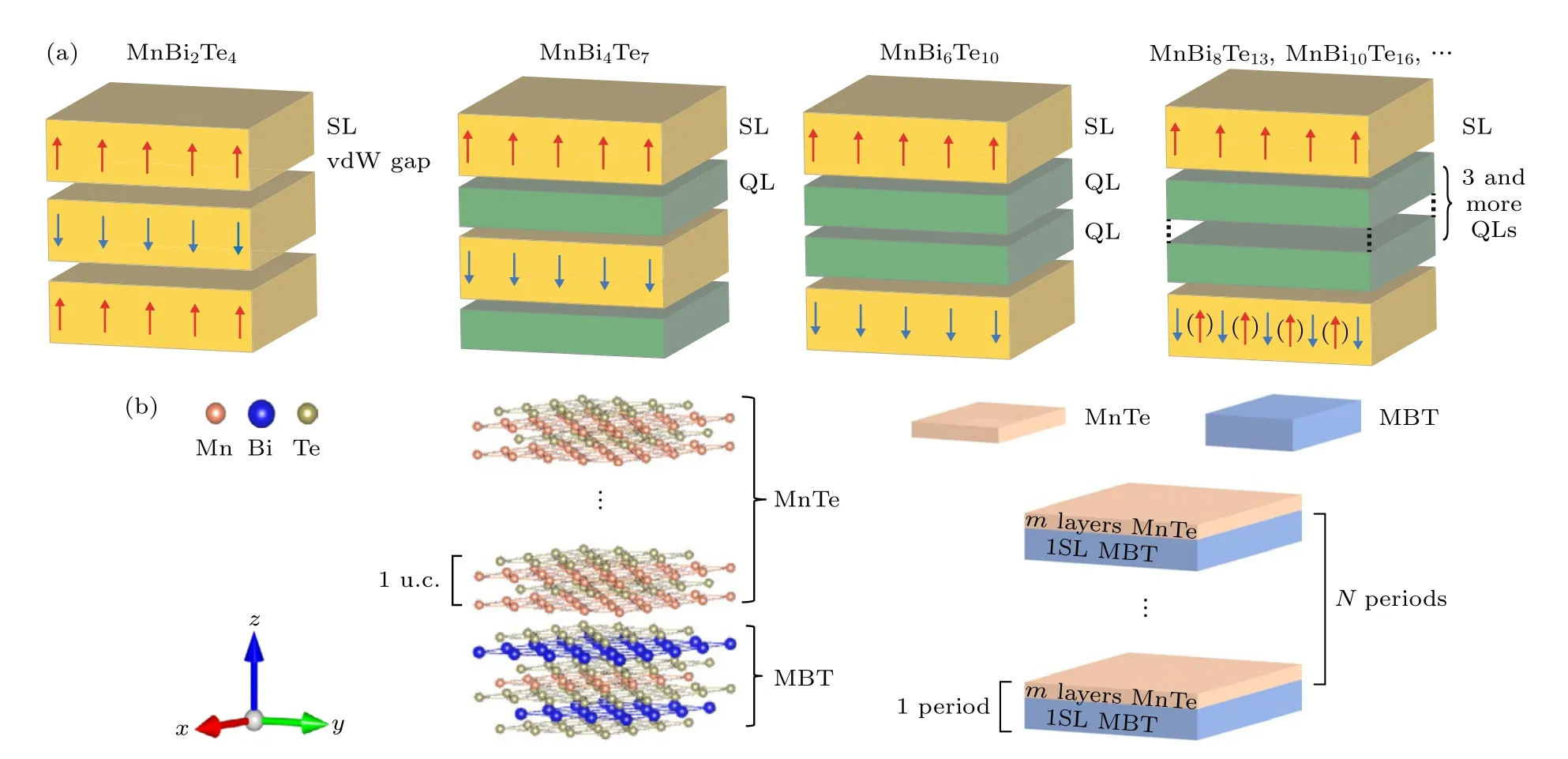
图10 (a) MnBi2Te4(Bi2Te3)n[95]和(b) MnBi2Te4(MnTe)m[96]的原子结构排列图Fig.10.Atomic structure of (a) MnBi2Te4(Bi2Te3)n[95] and (b) MnBi2Te4(MnTe)m[96] .

图11 (MnBi2Te4)m(Bi2Te3)n 体系丰富的拓扑物相 (a) (MnBi2Te4)m(Bi2Te3)n 体系拓扑相图[114].灰色、黄色和蓝色分别代表平庸的绝缘体、量子自旋霍尔态和量子反常霍尔态;(b) Mn-Bi-Te 体系随层间电子耦合和交换作用的不同展现丰富的拓扑物相[115]Fig.11.Rich topological phase in (MnBi2Te4)m(Bi2Te3)n system: (a) Topological phase diagram in (MnBi2Te4)m(Bi2Te3)n system[114].Gray,yellow,and blue represent normal insulators,quantum spin Hall states,and quantum anomalous Hall states,respectively;(b) phase diagram of the multilayer topological heterostructure Mn-Bi-Te systems in terms of relative spacing and magnetization[115].
4.2 Mn(Bi1−xSbx)2Te4
根据ARPES 的测量结果,MBT 样品总是表现出重n 型掺杂,即费米能级位于样品体态的导带中.这限制了其丰富拓扑物相的出现.从材料的角度出发,利用Sb 元素替代Bi 形成Mn(Bi1-xSbx)2Te4可有效将其费米能级从导带调控到价带,即载流子的类型从n 型转变为p 型,进而可以观测到其拓扑物性.不仅如此,Mn(Bi1-xSbx)2Te4还具有其他丰富物理现象[116],包括拓扑相变、金属绝缘转变、不同的磁性和反常朗道量子化[117]等,如图12(a)所示.因此,Mn(Bi1-xSbx)2Te4值得进一步研究,并可能在未来提供广泛的潜在应用.

图12 Mn(Bi1-xSbx)2Te4 的丰富物理现象及能带结构 (a) Mn(Bi1-xSbx)2Te4 的n-p 载流子转变和拓扑相变图[116];(b) 不同Sb 掺杂浓度的Mn(Bi1-xSbx)2Te4 样品的ARPES 测量的能带结构图[116,129]Fig.12.Rich physical phenomena and band structure of Mn(Bi1-xSbx)2Te4: (a) n-p carrier transition and topological phase transition diagram of Mn(Bi1-xSbx)2Te4[116];(b) band structure diagram of ARPES measurement of Mn(Bi1-xSbx)2Te4 samples with different Sb doping concentrations[116,129].
沈大伟及其合作者[116]发现在Mn(Bi1-xSbx)2Te4中,当掺杂量x=0.3 时,材料拥有相对较低的载流子浓度(3×1018cm-3).这表明费米能级处在带隙中.当Sb 完全取代Bi 时,MnSb2Te4(MST)的载流子为p 型(4×1020cm-3).因此,从体态电子结构的角度来看,Mn(Bi1-xSbx)2Te4系列样品可以调控费米能级、带隙,甚至能带反转[118],如图12(b)所示.由于组分和生长条件不同,MST 可以表现出反铁磁性(奈尔温度TN=20 K)[119]、铁磁性[120]、亚铁磁性[119,121](TC=25–34 K)甚至是混合磁有序[122].通过研究分析,推测这与每层内Mn 位和Sb 位间交换作用有关[119,123].Yan 等[124]报道,随着Mn(SbxBi1-x)2Te4中Sb 含量的增加,奈尔温度从MBT 的24 K 略微下降到MST 的19 K,而自旋翻转和磁矩饱和所需的临界磁场强度明显下降.Lei 等[125]建立了一种简单的模型解释膜厚、磁排列及堆叠序列对Mn(Bi1-xSbx)2Te4的磁性和拓扑性的影响;并通过密度泛函理论DFT 计算发现,完全有序的MST 是反铁磁性的,但拓扑上是平庸的.而另一项研究[126]表明在微过量Mn 掺杂Mn Sb2Te4(M-MST)中,Mn 部分取代Sb 使其兼具铁磁性和拓扑绝缘性,并且TC提高到了45–50 K.该样品具有垂直磁各向异性的铁磁性、2D Dirac锥,并且随着Mn 的微量掺杂量增加,其费米能级又从价带逐渐靠近Dirac 点.在TC以下,具有磁性导致的拓扑表面态带隙.Lee 等[127]在本征反铁磁拓扑绝缘体Mn(Bi1-xSbx)2Te4中观察到磁场导致的Type-II Weyl 态.此外,Wang 等[128]系统地测量了Mn(Bi1-xSbx)2Te4的电阻率、塞贝克系数和导热系数等,验证了当费米能级位于体隙内电荷中性点附近时,双极效应可能在其输运性质中起重要作用.
5 存在的问题
近几年,MBT 的电子结构还存在一些分歧,即MBT 的自然解理(001)晶面的拓扑表面态是否存在带隙[30,95].理论研究表明,由于该晶面的S对称性破缺,在TN以下,其拓扑表面态会出现带隙[15,31,112,130-132].早期的ARPES 测量结果[30,130,132]表明其拓扑表面态存在70–200 meV 的带隙.但有些研究组发现,在TN以下和以上,其拓扑表面态都无带隙[30,107,132-137].另有结果表明,拓扑表面态的带隙还会随空间位置的变化而变化[9,116,130].南方科技大学陈朝宇等[23]最近发表的一篇文章指出MBT 的拓扑表面态无磁隙的原因主要归类为两种: 磁重构和拓扑表面态重分布.1) 磁重构: 理论计算表明,在MBT 中,偏离A 型AFM-z的表层磁结构[49,104,134,138],例如无序磁结构、G-AFM 以及A 型AFM-x,都会导致无带隙的拓扑表面态.另一种类型的磁重构为磁畴和磁畴壁的形成[139].基于紧束缚模型的第一性原理[140]和实验[24]均证实了无带隙手性边缘态在相反磁畴存在时受到拓扑保护,因此这种边缘态是严格无带隙的.实验观察到MBT 表面存在磁畴壁[141,142],并且其拓扑表面态带隙大小与样品质量和空间位置相关[131,143].所以MBT 表面磁畴壁也可能导致无带隙的拓扑表面态.一种更复杂的亚铁磁结构已被实验观察到[119,144],并被用来解释MBT 中大大减小的拓扑表面态带隙[145].Mn-Bi 的互掺杂可以引入从表面数第二和第六原子层中MnBi的缺陷,其磁矩与中心Mn 层的磁矩反平行.由于拓扑表面态密度主要局域于Te-Bi-Te 层,MnBi的缺陷磁矩抵消了部分中心Mn 层的磁矩,这导致拓扑表面态带隙减小.MnBi缺陷的不均匀性可以解释拓扑表面态带隙大小与样品质量和空间位置的依赖性,这表明改善样品晶体质量进而抑制Mn-Bi 的互掺杂是近期研究的关键问题[145].此外,贡献磁性的Mn d 轨道和贡献拓扑表面态的Bi/Te p 轨道间的弱耦合[135]也可能导致MBT 无带隙的拓扑表面态.2) 拓扑表面态重分布: 无带隙的拓扑表面态也可归因于拓扑表面态从最顶层SL 到下一层的扩展分布使得拓扑表面态感受到的有效磁矩减小.导致拓扑表面态重分布的内因有能带杂化[146],vdW 间距膨胀[147,131]和电荷[143]/缺陷[148]效应等.拓扑表面态与Rashba劈裂能带杂化会引起拓扑表面态的重分布[146],进而产生无带隙的表面态.在理想情况下,拓扑表面态主要位于最顶端的SL.在A-AFM 结构中,拓扑表面态的有效磁矩约等于最顶层SL 的净铁磁矩,这足以像预期的那样打开一个相当大的拓扑表面态Dirac 带隙.然而在实际情况中,拓扑表面态的分布扩展到第二个SL 层.层间反铁磁排列导致前两个SLs 的净磁化为零,从而抵消了拓扑表面态感受到的有效磁矩.在极端情况下,不论表面AAFM 磁结构多么稳固、磁有序与能带耦合多么强,若拓扑表面态平均分布在前两个SLs,则无带隙拓扑表面态出现[23].
该领域面临的另一个问题是大面积MBT 薄膜样品的质量不高,进而影响其拓扑量子态的观测.到目前为止,验证MBT 的量子反常霍尔效应、轴子绝缘体态等拓扑量子态的样品几乎都是块体MBT 单晶手撕的薄片.但手撕薄片的形状不规则、尺寸较小、性能调控不良并且产率低,这使得MBT 材料体系性能的系统研究及优化非常困难,导致不同的样品测量数据不一致,不利于促进其实际的拓扑应用.为了开发其拓扑应用,需要以可重复、可控和可扩展的方式制备MBT 样品,使其能够构建复杂的、大面积的异质结构和阵列等,进而实现不同用途.而薄片状样品很难满足要求.分子束外延是目前最精密的制备高质量薄膜的方法之一,可提供大面积、规则并且易于调控的样品,满足重复性、可调性和可扩展性的制备需求[149].自2018 年何珂研究组[29]首次使用分子束外延制备成功MBT 薄膜以来,一直未在使用分子束外延制备的MBT 样品中[150,151]观测到这些奇异的拓扑量子态.直到近期,清华大学的冯硝研究组[149]使用分子束外延制备了MBT 薄膜,并在高磁场下的铁磁MBT 薄膜中测试到量子化的霍尔电阻率.因此,继续探索MBT 制备高质量大面积致密的MBT 薄膜尤为重要.
6 总结与展望
本文简要回顾了本征磁性拓扑绝缘体MBT的基本性质,重点介绍了其奇异的拓扑量子态: 量子反常霍尔效应、轴子绝缘体、手性马约拉纳模等.对本征磁拓扑绝缘体MBT 的研究具有重要的科学价值和应用前景,因其在无耗散自旋电子学、信息存储和量子计算方面的巨大潜力.当前MBT 体系的研究正在如火如荼地开展,并不断涌现一些重要的成果.MBT 系列的发现只是磁性拓扑物理研究的开端,预期更多新的磁性拓扑物理效应和理想磁性拓扑体系会被发现.通过掺杂、应变、缺陷工程、加压、异质结和超晶格构建等手段,MBT 及其相关体系的磁性、电学等性质有望进一步改善,这也为更多新奇拓扑量子物态的研究提供了绝佳平台.其次,由于MBT 还存在磁转变温度低、重n 型掺杂等问题,寻找具有更高磁转变温度、更优的本征磁性拓扑性质的新材料体系有望在更高温度下实现拓扑量子态,进而更接近实际应用.不局限于在拓扑材料中引入磁性,反过来在磁性材料中寻找拓扑性将有可能更有效地发现本征磁性拓扑材料[44].高通量计算和磁空间群分析预测大量新的磁性拓扑材料[152-156],为相关实验提供指导.研究不同的磁性(铁磁、反铁磁、亚铁磁和新的磁化状态等)与拓扑性相互作用可能产生更多奇异拓扑量子态等.本征磁性拓扑绝缘体不仅为研究拓扑磁有序结构和新颖的拓扑相变提供理想平台,而且对物理学、材料和信息技术领域的发展具有重要的推动意义.
感谢南方科技大学量子研究院陈朝宇研究员和王渊博士的讨论.
