基于Wiener模型和Wiener-Hammerstein模型的非线性动态过程完整建模方法

王珠　刘志辉　肖既磊

摘 要 基于Wiener模型和Wiener-Hammerstein模型提出Wiener结构神经网络（WienerNN）模型和Wiener-Hammerstein结构神经网络（WHNN）模型，推导了Wiener模型和Wiener-Hammerstein模型的泛化能力，并给出了模型神经网络化的全过程。将所推导出的WienerNN模型和WHNN模型用于单变量和多变量非线性动态过程建模，验证了模型的有效性。

关键词 非线性动态系统 神经网络 Wiener模型 Wiener-Hammerstein模型

中图分类号 TP271   文献标志码 A   文章编号 1000-3932（2023）05-0652-08

非线性动态系统辨识是目前系统辨识领域研究的难点和焦点问题［1～3］，其主要难点在于缺乏描述一般非线性系统的统一的数学模型。为此，研究学者们提出了多种类型的系统模型，如支持向量机模型［4］、小波网络［5］、神经网络模型［6～8］及Volterra级数［9，10］等。虽然这些非线性动态建模方法具体实现的方式不同，但都存在相同的问题：动态与非线性之间的相互融合关系限制了模型的泛化能力和估计精度［11］。

为此，笔者基于分离性建模方法Wiener模型［12，13］和Wiener-Hammerstein模型［14］设计了Wiener结构神经网络（Wiener Structured Neural Network，WienerNN）模型和Wiener-Hammerstein结构神经网络（Wiener-Hammerstein Structured Neural Network，WHNN）模型。同时，考虑到神经网络模型权重参数初始值的设置对模型的预测精度和收敛速度具有一定影响，因此在模型训练过程中，首先采用粒子群算法进行初步全局寻优，目的是得到较优的参数初始值，进而使用基于时间的反向传播算法（Back-Propagation Through Time，BPTT）进行参数优化。最后，将所推导出的WienerNN模型和WHNN模型用于非线性动态过程建模，并与基线模型GRU和RNN进行结果对比，以验证笔者所提模型的有效性。

1 分离性模块化建模的使用范围与可行性分析

1.1 模塊化非线性系统结构

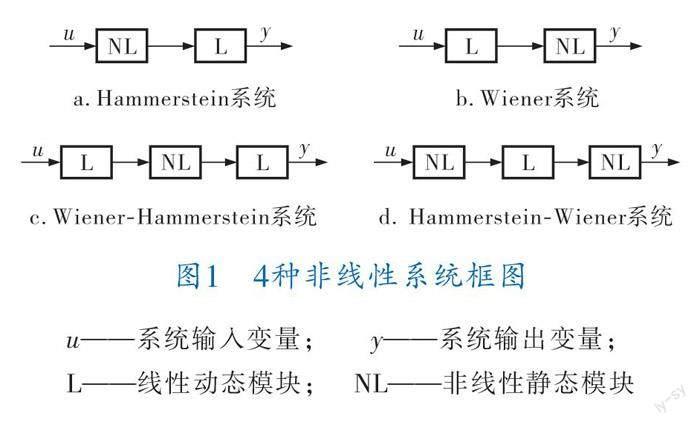
传统模块化非线性系统，也称为简单模块化非线性系统，由线性动态模块和非线性静态模块按照不同的形式级联而成，图1所示的4种非线性系统均属于这类系统。这类系统也是目前研究最多的一类模块化非线性系统，它们为解决许多实际非线性问题提供了一种非常有效的结构形式。

采用分离性建模方法描述系统时需先满足以下两个假设条件：

a. 过程中的动态特性能够被输入动态与输出动态充分表达；

b. 从系统中分离出的非线性能够尽可能充分地表达过程中的非线性。

1.2 Wiener模型

Wiener模型由一个线性动态模块后接一个非线性静态模块组成，能够表征大量的非线性系统。单变量Wiener模型的一般形式如下：

5 结束语

基于Wiener模型和Wiener-Hammerstein模型建立了新型神经网络模型WienerNN和WHNN，推导了Wiener模型和Wiener-Hammerstein模型的泛化能力，并给出了模型神经网络化的全过程，同时介绍了WHNN模型的训练原理、算法和流程。仿真实验结果表明，与GRU和RNN相比，对于一类Wiener过程，即输出非线性过程，WienerNN模型具有更高的预测精度；对于一类Wiener-Hammerstein过程，WHNN模型具有更高的预测精度；对于非线性与动态特性很难分离的一类系统，WienerNN和WHNN模型均能够很好地跟踪系统输出，但WienerNN模型更为合适。

后续工作中笔者将收集实际现场数据，利用更加高效的训练算法对WienerNN和WHNN模型进行训练，以进一步验证模型的有效性。

参 考 文 献

［1］   KOUKOULAS P，KALOUPTSIDIS N.Nonlinear system identification using Gaussian inputs［J］.IEEE Transactions on Signal Processing：A Publication of the IEEE Signal Processing Society，1995，43（8）：1831-1841.

［2］   冯培悌.系统辨识［M］.2版.杭州：浙江大学出版社，2004.

［3］   SI H N，SHAO X L，ZHANG W D.Fuzzy rule-based neural appointed-time control for uncertain nonlinear systems with aperiodic samplings［J］.Expert Systems with Applications，2021，170.DOI：10.1016/j.eswa.2020.

114504.

［4］   田中大，高宪文，石彤.用于混沌时间序列预测的组合核函数最小二乘支持向量机［J］.物理学报，2014，63（16）：70-80.

［5］   宋彤，李菡.基于小波回声状态网络的混沌时间序列预测［J］.物理学报，2012，61（8）：90-96.

［6］   NARENDRA K S，PARTHASARATHY K.Identificat-ion and control of dynamical systems using neural networks［J］.IEEE Transactions on Neural Networks，1990，1（1）：4-27.

［7］   LEVIN A U，NARENDRA K S.Control of nonlinear dynamical systems using neural networks.Ⅱ.Observab-ility，identification，and control［J］.IEEE Transactions on Neural Networks，1996，7（1）：30-42.

［8］   赵小国，刘丁，景坤雷.融合改进蚁狮算法和T-S模糊模型的噪声非线性系统辨识［J］.控制与决策，2019，34（4）：759-766.

［9］   彭志科，程长明.Volterra级数理论研究进展与展望［J］.科学通报，2015，60（20）：1874-1888.

［10］  JANJANAM L，SAHA S K，KAR R，et al.Global Gravitational Search Algorithm-Aided Kalman Filter Design for Volterra-Based Nonlinear System Identifi-cation［J］.Circuits，Systems，and Signal Processing，2021，40（5）：2302-2334.

［11］   TOTTERMAN S，TOIVONEN H T.Support vector me-thod for identification of Wiener models［J］.Journal of Process Control，2009，19（7）：1174-1181.

［12］   曹鹏飞，罗雄麟.基于Wiener结构的软测量模型及辨识算法［J］.自动化学报，2014，40（10）：2179-2192.

［13］   WANG Z， ZHAO L K，LUO X L. Wiener structure based adaptive control for dynamic processes with approximate monotonic nonlinearities［J］.Journal of the Franklin Institute，2020，357（18）：13534-13551.

［14］   JANJANAM L， SAHA S K， KAR R，et al.Optimal design of cascaded Wiener-Hammerstein system using a heuristically supervised discrete Kalman filter with application on benchmark problems［J］.Expert Systems with Applications，2022，200.DOI：10.1016/j.eswa.2022.117065.

［15］   KUMARI R，EKBAL A.AMFB：Attention based mult-imodal Factorized Bilinear Pooling for multimodal Fake News Detection［J］.Expert Systems with Appli-cation，2021，184：115412.1-115412.12.

［16］   賈立，李训龙.Hammerstein模型辨识的回顾及展望［J］.控制理论与应用，2014，31（1）：1-10.

［17］   HOU J，LIU T，WAHLBERG B，et al.Subspace Ham-merstein Model Identification under Periodic Distur-bance［J］.IFAC-PapersOnLine，2018，51（15）：335-340.

（收稿日期：2022-11-25，修回日期：2023-07-25）

A Complete Modeling Method for Nonlinear Dynamic Processes

Based on Wiener Structured Neural Network and Wiener-

Hammerstein Structured Neural Network

WANG Zhu， LIU Zhi-hui， XIAO Ji-lei

（College of Information Science and Engineering， China University of Petroleum（Beijing））

Abstract   Having Wiener model and Wiener-Hammerstein model based to propose Wiener structured neural network（WienerNN） model and Wiener-Hammerstein structured neural network（WHNN） model was implemented， including the derivation of generalization ability of the Wiener model and the Wiener-Hammerstein model， as well as the presentation of the whole process of model neural network. Applying both WienerNN model and WHNN model derived to model univariate and multivariable nonlinear dynamic processes can verify both feasibility and effectiveness of the model proposed.

Key words   nonlinear dynamic system， neural network， Wiener model， Wiener-Hammerstein model

基金项目：国家自然科学基金项目（61703434）。

作者简介：王珠（1989-），副教授，从事过程动态建模与辨识、智能控制与故障预警以及机器学习与神经网络等的研究。

通讯作者：刘志辉（1998-），硕士研究生，从事过程动态建模与辨识、神经网络等的研究，15750490146@163.com。

引用本文：王珠，刘志辉，肖既磊.基于Wiener模型和Wiener-Hammerstein模型的非线性动态过程完整建模方法［J］.化工自动化及仪表，2023，50（5）：652-659.