改进Laplace先验下的复数域多任务贝叶斯压缩感知方法*

张启雷,孙 斌

(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 北京跟踪与通信技术研究所, 北京 100094)

稀疏贝叶斯学习(sparse Bayesian learning,SBL)理论已经发展成为信号处理领域的一个重要分支[1-4]。SBL理论与压缩感知相结合催生了一类重要的稀疏信号重构算法,即贝叶斯压缩感知(Bayesian compressive sensing,BCS)方法[5-7]。BCS方法的应用领域相当广泛,包括阵列设计、波束形成和雷达成像等[8-10]。

SBL又被称为相关向量机(relevance vector machine,RVM),具有良好的全局最优和局部最优特性[3]。研究表明,SBL等价于一种加权的1范数算法,因此是一类精确性和鲁棒性更好的稀疏重构算法[11]。文献[5]将SBL理论应用到压缩感知领域,并提出了BCS技术。随后,BCS被进一步扩展到多任务压缩感知领域[6]。文献[7]基于分层Laplace先验分布,提出了一种改进的BCS方法。基于上述研究,实数域的BCS理论框架已经基本完善了。然而,现有的实数域BCS方法无法直接解决复数域稀疏信号重构问题。

为了利用BCS理论实现复数域稀疏信号重构,文献[12-13]给出了一种直观的解决思路,即将复数分解为实部和虚部,分别利用现有的实数域BCS方法进行求解,最后将两部分结果合成为复数。在此基础上, 文献[14]假设复数的实部和虚部具有相同的稀疏特性,提出了一种复数域多任务BCS(complex multitask Bayesian compressive sensing, CMT-BCS)算法。然而,由于复数分解,测量矩阵和信号的维度都被扩大了,上述算法的存储量和计算量明显增加。此外,复数分解不可避免地破坏了原始复数信号的内部结构,因此稀疏重构结果难以令人满意。

与上述算法不同,本文直接在复数域推导并构建BCS理论框架。首先,基于改进的分层Laplace先验和多任务学习模型,建立了复数域贝叶斯压缩感知模型;其次,通过边缘积分消除了测量噪声方差的影响,提出了一种复数域贝叶斯压缩感知方法;再次,利用矩阵分解理论,推导了一种基于递归操作的快速算法;最后,利用数值仿真实验验证了本文提出的改进Laplace先验下的复数域多任务贝叶斯压缩感知(complex multitask Bayesian compressive sensing algorithm using modified Laplace priors, CMBCS-MLP)方法的有效性。

1 问题描述

1.1 多任务学习模型

本文考虑一种多任务学习场景,假设不同任务之间是统计相关的,且共享相同的先验参数。复数域多任务贝叶斯测量模型可以表示为

yi=Φixi+ni

(1)

其中:i=1,2,…,L表示任务索引,L代表任务数目;yi∈Ni表示复数域压缩观测数据,Φi∈Ni×M表示复数域测量矩阵,xi∈M表示复数域原始信号,ni∈Ni代表复数域测量噪声,Ni≪M。

根据BCS理论框架,如果xi满足某种合适的稀疏先验分布,则可以利用贝叶斯原理得到该信号的后验概率,进而从压缩后的观测数据yi中恢复出稀疏原始信号xi[1-3]。

1.2 改进的分层Laplace先验

根据贝叶斯理论观点,所有的未知变量均可以看作满足一定概率分布的统计量[1,15]。

首先,假设ni满足零均值复高斯分布,且方差为σ2。令β=σ-2,则复数域观测数据的条件概率分布函数可以表示为

p(yi|xi,β)=CN(yi|Φixi,β-1)

(2)

其中,CN(·)代表多变量复高斯分布,先验参数β满足Gamma先验分布

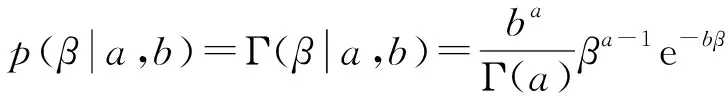
(3)

然后,假设原始信号xi满足某种稀疏先验分布。文献[7]已经证明,相比于RVM中的先验分布[1],分层Laplace分布是一种性能更优的先验分布。然而,直接沿用文献[7]提出的分层Laplace先验设置得到的BCS算法受测量噪声方差,即先验参数β的影响。如果β的初始值设置不合理,BCS算法存在性能恶化的危险。然而,通过改进原始信号xi的先验分布形式,可以消除参数β的影响,进而得到一种改进的BCS算法[6]。

第一层,假设xi满足特殊的多变量零均值复高斯分布

(4)

其中,α为先验参数,|xi,m|表示xi的第m个元素的绝对值。 第二层,假设α先验参数满足一种特殊的Gamma分布

(5)

其中,αm>0,且λ>0。 综上,原始信号xi的先验分布可以表示为

可以看出,经过分层先验设置,复数域原始信号xi满足Laplace先验分布。第三层,假设超先验参数λ满足一种特殊分布p(λ)=1/λ[7]。

综上,图1给出了基于改进的分层Laplace先验的复数域多任务学习贝叶斯模型图。可以看出,该贝叶斯模型分为三层:底层为复数域多任务信号模型,中间层为由多个任务共享的先验参数,顶层为超先验参数,用来控制中间层的先验参数。本文中先验参数和超先验参数同称为超参数(hyper-parameters)。

图1 基于改进Laplace先验的复数域多任务贝叶斯压缩感知模型图Fig.1 The graphical model of complex multitask Bayesian compressive sensing using modified Laplace priors

2 CMBCS-MLP方法

2.1 贝叶斯推断

根据BCS理论,原始信号的稀疏重构是通过使其后验概率最大得到的。图1中未知变量的后验概率分布可以表示为

(7)

其中,{xi}和{yi}分别代表原始信号集和观测数据集。通常,很难直接得到p({xi},α,β,λ|{yi})的解析表达式[1]。然而,根据贝叶斯原理

p({xi},α,β,λ|{yi})

=p({xi}|{yi},α,β,λ)·p(α,β,λ|{yi})

(8)

根据式(8),可以得到一种实用的贝叶斯推断方法。

假设超参数α和β已知,则原始信号xi的后验概率分布可以表示为

(9)

根据式(2)和式(4),可以得到

p(xi|yi,α,β)=CN(xi|μi,β-1Σi)

(10)

其中

(11)

A=diag(α1,α2,…,αM)是对角矩阵。

进而,基于1.2节建立的特殊先验分布,可以通过边缘积分消去参数β的影响,即

(12)

可以看出,通过边缘积分消去超参数β之后,xi的后验概率分布从式(10)给出的多变量复高斯分布变为式(12)给出的多变量Student-t分布[6]。 根据Student-t分布的性质,xi的后验期望仍然为μi。 然而,相比于高斯分布,Student-t分布具有更尖锐的峰值和更长的拖尾[1,6],这意味着改进后的算法具有更好的稀疏重构性能。 此外,消除了测量噪声方差的影响之后,式(12)中给出的稀疏重构算法鲁棒性更好。

2.2 超参数估计

本节基于经验贝叶斯(empirical Bayesian)方法[1],给出超参数估计方法。 为了估计超参数α和λ,需要利用所有的观测数据集{yi}。 根据贝叶斯原理,p(α,λ|{yi})∝p({yi},α,λ),且

(13)

因此,通过使p({yi},α,λ)最大化可以得到上述超参数的点估计值。

根据式(2)和式(3),可以得到

=CN(yi|0,β-1Bi)

(14)

(15)

为了方便推导,下面将p({yi},α,λ)的对数值作为代价函数

L(α,λ)=lnp({yi},α,λ)

(16)

其中,C为常数。对L(α,λ)分别关于αm和λ求导,并令导数为零,可以得到两者的点估计值为

(17)

然而,需要指出的是,上述迭代算法涉及矩阵求逆运算,运算量较大。尤其对于高维度的信号,该算法的运算量是难以承受的。因此,为了提高该算法的实用性,有必要研究其快速算法。

3 基于矩阵分解理论的快速算法

如前所述,在迭代算法中,最主要的计算量来自式(11)中Σi的求解,不仅涉及矩阵求逆运算,还需要在每次迭代中更新α中全部的元素。事实上,文献[2]已经证明,更新α中单个元素也可以实现代价函数L(α,λ)的有效更新。因此,通过序贯地增加、删除或重新估计α中的某一个元素,可以实现超参数α的有效估计,最终找到原始信号xi中所有有效的xi,m,即实现稀疏重构。

3.1 算法推导

根据矩阵分解理论[2],矩阵Bi可以写为

(18)

(19)

只考虑L(α,λ)中α的影响,则可以得到

L(α)=L(α-m)+(αm)

(20)

其中,L(α-m)与αm无关,而(αm)可以表示为

(21)

其中

(22)

因此,可以得到

(23)

理论上,令式(23)等于零可以得到αm的点估计值。然而,除αm=∞这个解之外,很难得到αm的其他解析解。文献[2]已经证明,通常αm≪si,m,因此可以得到

(24)

其中

(25)

通过求解式(24),可以得到αm的近似解为

(26)

基于式(26),可以得到一种基于递归操作的复数域多任务贝叶斯压缩感知快速算法。在每次的递归操作中,只需要更新一个候选的αm,因此μi和Σi的更新很高效,同时λ也可以同步更新。实际中,通常选择使(αm)值最大的αm作为候选参数,可以获得更快的收敛速度[5-7]。

3.2 误差分析

在上述推导中,为了得到αm的解析解,假设αm≪si,m,进而得到近似等式(24),因此必须分析该假设带来的近似误差。

在式(23)的基础上,进一步求解代价函数L(α)的二阶导数可得

(27)

然而,上述分析是建立在假设αm≪si,m的基础之上的。虽然文献[2]和文献[6]已经证明了该假设的有效性,但只能保证式(26)给出的近似解位于(αm)的局部最大值点附近,因此上述近似处理是次优的。尽管如此,已有文献[2,5-7]和本文的数值仿真均表明上述快速算法的精确性和有效性是足够的。

3.3 计算复杂度分析

本节基于矩阵分解理论推导了一种基于递归操作的快速算法,相比于第2节的迭代算法,可以有效降低计算复杂度。

针对第2节给出的迭代算法,最主要的计算量来自式(11)中的矩阵求逆。矩阵Σi的维度为M×M,因此求逆运算的计算复杂度为Ο(M3)[5]。随着M的增大,该计算复杂度急剧增加。本节提出的快速算法采取递归操作,每次只针对α中的一个元素进行计算,直到找到α中所有的有效元素,操作次数近似等于压缩观测数据的维度Ni。详细分析表明[2]:基于递归操作的快速算法的计算复杂度为Ο(NiM2)。由于Ni≪M,因此相比于第2节的迭代算法,本节给出的快速算法计算复杂度大大降低。

4 数值仿真

单任务学习可以视作多任务学习的特例, CMBCS-MLP方法同样适用于单任务学习场景,此时令L=1即可。首先,面向单任务学习场景,针对两种不同的复数域信号进行稀疏重构实验,并与文献[12-13]给出的实数域BCS方法 (记为RBCS)和文献[14]提出的CMT-BCS方法的重构结果进行对比。为了便于对比,在仿真中,a=100/E{VAR(yi)},b=1,其中VAR(·)代表求方差,E{·}代表求均值。

第一种信号为复数域均匀尖峰信号,长度M=512,其实部和虚部分别包含30个位置随机出现的尖峰,尖峰幅度为1或-1。测量矩阵Φi的生成分为两步:首先,生成服从复高斯分布CN(0,1),维度为Ni×M的复矩阵,Ni=100;然后,对该复矩阵沿行进行幅度归一化处理。测量噪声ni的实部和虚部均满足零均值高斯分布,且标准差为σ=0.005。稀疏重构实验的结果如图2所示,由于篇幅所限,图中只给出了复数域信号的幅度。其中RBCS、CMT-BCS、CMBCS-MLP方法的重构误差分别为eRBCS=1.226 7、eCMT-BCS=0.255 3、eCMBCS-MLP=0.016 9。

(a) 原始信号(a) Original signal

(b) RBCS方法重构结果(b) Reconstruction result using RBCS

(c) CMT-BCS方法重构结果(c) Reconstruction result using CMT-BCS

(d) CMBCS-MLP方法重构结果(d) Reconstruction result using CMBCS-MLP图2 复数域均匀尖峰信号重构结果 (Ni=100, M=512)Fig.2 Reconstruction result of complex uniform spikes(Ni=100, M=512)

第二种信号为复数域非均匀尖峰信号,长度M=512,其实部和虚部分别包含30个位置随机出现的尖峰,尖峰的幅度满足零均值高斯分布,且与均匀尖峰信号的功率相等。测量矩阵Φi和测量噪声ni的生成方法与前文相同。稀疏重构实验的结果如图3所示。其中RBCS、CMT-BCS、CMBCS-MLP方法的重构误差分别为eRBCS=0.023 5、eCMT-BCS=0.099 5、eCMBCS-MLP=0.015 5。

(a) 原始信号(a) Original signal

(b) RBCS方法重构结果(b) Reconstruction result using RBCS

(c) CMT-BCS方法重构结果(c) Reconstruction result using CMT-BCS

(d) CMBCS-MLP方法重构结果(d) Reconstruction result using CMBCS-MLP图3 复数域非均匀尖峰信号重构结果(Ni =100,M=512)Fig.3 Reconstruction result of complex non-uniform spikes(Ni=100,M=512)

由图2和图3可以看出,针对两种不同的复数域稀疏信号, CMBCS-MLP方法均给出了最优的重构结果。然而,图2和图3给出的结果仅是随机过程的一次实现,不具有普遍意义。此外,除重构精度外,计算耗时也是重构算法的重要指标。分别针对上述两种复数域稀疏信号,利用蒙特卡罗方法开展重构实验,实验重复次数为100次。不同BCS算法的重构性能如表1所示。可以看出: CMBCS-MLP在重构精度和计算耗时两个方面均是最优算法,而RBCS算法的性能最差。虽然CMT-BCS针对复数域均匀尖峰信号给出了较好的重构结果,但计算耗时是最长的;而对复数域非均匀尖峰信号,CMT-BCS的重构误差和计算耗时两项指标均是最差的。究其原因是,RBCS和CMT-BCS算法人为破坏了复数信号的内部结构,造成算法鲁棒性较差、耗时较长;而本文提出的CMBCS-MLP算法直接在复数域进行重构,克服了上述缺陷,因此算法鲁棒性较好,计算耗时较短。

最后,通过多任务学习模型来验证CMBCS-MLP方法在多任务学习中的优势。假设两个复数域均匀尖峰信号的参数与前文相同,长度均为M=512。一个特殊的设置在于这两个复数域信号有80%的尖峰位于相同的位置,即二者的相似性为80%。两个信号的测量次数分别为N1=70和N2=75。测量矩阵Φi和测量噪声ni的生成方法与前文相同。稀疏重构实验的结果如图4所示。可以看出:由于观测数据较少,观测噪声较大,采用单任务学习CMBCS-MLP方法重构结果误差较大,无法恢复原始信号;而多任务学习CMBCS-MLP方法充分利用了两个复数域信号之间的相似性,准确恢复了两个原始信号。

(a) 原始信号x1和x2(a) Original signal x1 and x2

(b) 单任务算法重构结果 x1和x2(b) Reconstruction results of x1 and x2 using single-task algorithm

(c) 多任务算法重构结果x1和x2(c) Reconstruction results of x1 and x2 using multitask algorithm图4 多任务学习场景下的CMBCS-MLP方法重构结果(Ni=100,M=512)Fig.4 Reconstruction result of CMBCS-MLP for the multitask learning setting (Ni=100,M=512)

5 结论

现有的BCS理论框架是在实数域推导和建立的,因此无法直接用于复数域稀疏信号重构。针对这个问题,本文直接在复数域推导BCS方法。基于改进的分层Laplace先验和多任务学习模型,本文在复数域推导了一种CMBCS-MLP方法,并基于矩阵分解理论给出了其快速算法。理论分析和数值仿真表明:针对复数域稀疏信号重构问题,相比于现有的实数域BCS方法,CMBCS-MLP方法具有更好的精确性和鲁棒性。下一步研究的重点在于将CMBCS-MLP方法应用到具体的复数域信号处理问题中,进一步拓展BCS技术的应用范畴。