闪烁噪声条件下基于交互多模框架的雷达目标跟踪算法*

占荣辉,李祖检,滕书华

(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 湖南第一师范学院 电子信息学院, 湖南 长沙 410205)

通常情况下,雷达传感器的测量误差主要受系统噪声和处理方法的影响,相应的噪声可称为“常规噪声”。但当雷达对复杂运动目标进行探测时,由于目标与传感器之间的几何关系将动态发生变化,目标上不同散射中心的相对相位也会随机发生变化,从而造成回波相位波前的畸变。波前在观测方向上的倾斜和随机摆动现象被称为闪烁效应,由此导致的测量噪声常被称为“闪烁噪声”。理论上,凡尺度能与雷达波长相比拟,具有两个或两个以上散射中心的任何体目标都可能产生闪烁效应,且目标与传感器越近,因闪烁效应产生的量测噪声也就越大。这对诸如导弹制导等应用场合极为不利,将严重影响制导控制精度,甚至会引起导弹脱靶。

与常规噪声的高斯分布特性不同,闪烁噪声具有明显的拖尾特性,是典型的非高斯噪声。目前,关于闪烁噪声的分布主要有高斯-拉普拉斯混合模型[1]、混合高斯模型[2-4]、t分布模型[5-7]、高斯-t混合分布模型[8-9]等。文献[10]采用QQ-plot方法对闪烁噪声进行拟合,得到了模型参数的估计结果。值得一提的是,雷达的测量结果是在极坐标(或球坐标)下得到的,而观测方程具有非线性特点,因此闪烁噪声条件下的目标跟踪问题是典型的非线性、非高斯问题。

众所周知,卡尔曼滤波器(Kalman filter, KF)是线性、高斯假设条件下的最优状态估计器,在目标跟踪领域得到广泛的应用。在非线性、非高斯条件下,最优化滤波假设不再成立,国内外学者对此展开了广泛的研究。在现有针对闪烁噪声的跟踪算法中,根据原理框架的不同,可粗略分为以下三类:

第一类是以非线性评分函数(score function)为基础的跟踪算法。在文献[11]中,作者最早通过引入评分函数对KF进行修正。作为一种早期提出的方法,该算法涉及烦琐的混合分布函数卷积操作,在系统状态维数较高时异常复杂,因此在实际中应用较少。为此,文献[1]在评分函数的基础上,通过将量测噪声分布进行正交展开来避免卷积操作,然而该算法需要对量测向量进行解耦合,同时也存在复杂的矩生成函数(moment generating function, MGF)计算问题,因此实用性也较差。

第二类是以高斯混合(Gaussian mixture, GM)或高斯和(Gaussian sum, GS)滤波为基础的跟踪算法[12-13]。这类算法将目标状态、过程噪声、测量噪声分别用多个高斯分量来近似,并采用多个并行的高斯近似滤波器完成状态估计。高斯近似滤波器的具体实现形式有扩展卡尔曼滤波器(extended KF, EKF)、不敏卡尔曼滤波器(unscented KF, UKF)和容积卡尔曼滤波器(cubature KF, CKF)等[14-15]。该类算法的优点是实现结构比较简单,不足之处是:高斯分量数会随递推步数(时间周期数)呈指数增长,因此在每步递推完成后,需要进行高斯分量剪枝和合并处理;对高斯分量数的确定缺乏严格的理论指导,只能通过人工经验进行选择优化。

第三类是以粒子滤波(particle filter, PF)为基础的跟踪算法[16-18]。这类算法主要利用了粒子滤波器对非线性、非高斯系统具有强大的近似能力这一特点,采用概率分布近似(而不是函数近似)手段进行目标状态估计。粒子的采样通常有两种方式:一是直接通过先验分布(状态转移函数)进行采样,这种采样方式比较简单,但粒子质量不高;二是从融合了量测信息的重要采样函数或建议分布[19-21]中进行采样,该采样方式虽能在一定程度上改善粒子质量,但每一个粒子都需一个类卡尔曼滤波器(卡尔曼滤波器及各种衍生形式)来实现完整的状态递推,导致算法复杂度急剧上升。除此之外,对于高维目标状态(相对一维标量状态),若要达到理想的密度近似效果和良好的跟踪性能,粒子规模必须足够大,相应地,算法的复杂度也会非常高。

事实上,虽然闪烁噪声被建模为各种混合分布的形式,但闪烁噪声的发生本质上是概率事件。若将出现“常规噪声”和“闪烁噪声”视为两个不同的事件,对应两种不同的观测误差模型,同时将两种噪声出现的概率视为模型概率,并用一阶马尔可夫模型对相邻时刻噪声分布的变化特性进行建模,则可利用交互多模(interacting multiple model, IMM)框架[22-23]进行处理,解决传统高斯混合滤波算法中对高斯分量选择缺乏理论指导、存在模型适配性差的问题。

受此思路启发,本文以闪烁噪声的高斯混合分布建模为基础,提出了一种交互多模框架下的高性能跟踪滤波算法。该算法用一个高斯分量对应一种噪声分布模型,同时通过一阶马尔可夫模型建立转移概率矩阵,并用免导数运算、对非线性系统具有强适应能力的容积卡尔曼滤波器与不同高斯分量相对应的模型匹配滤波,最后对各匹配滤波结果进行综合得到最终的跟踪结果。仿真结果证明了所提方法的有效性,并通过与传统高斯混合滤波算法、粒子滤波算法等进行比较说明了本文方法的性能优势和执行效率优势。

1 问题描述

考虑典型的目标跟踪系统,目标离散时间状态演化方程可描述为

xk=f(xk-1)+wk-1

(1)

其中:xk∈nx为nx维状态矢量,通常包括目标位置、速度等分量;f(·)为状态转移方程;wk-1为高斯过程噪声,其均值为零,协方差矩阵为Qk-1,简记为wk-1～N(wk-1;0,Qk-1)。

相应地,目标观测方程可描述为

zk=h(xk)+vk

(2)

式中:zk∈nz为nz维观测矢量,通常包含目标距离、角度等分量;h(·)为观测方程;vk为观测噪声。

通常情况下,vk被视为均值为零、协方差矩阵为Rk的高斯观测噪声。但在雷达受到干扰、复杂目标姿态发生急变等条件下,测量误差会出现跳变,称为“闪烁”,测量噪声的高斯分布特性不再满足。此时,常用的处理方法是将闪烁噪声建模为混合高斯分布,即

p(vk)=(1-ε)p1(vk)+εp2(vk)

(3)

2 混合高斯滤波算法

1)预测:假定k-1时刻状态的后验PDF为p(xk-1|z1:k-1),则其一步前向预测的PDF可根据Chapman-Kolmogorov方程计算为

(4)

式中,p(xk|xk-1)称为状态的转移密度函数,用于描述一阶马尔可夫过程。

2)更新:在获得p(xk|z1:k-1)的基础上,综合新近的观测zk,可通过式(5)所示的贝叶斯规则计算k时刻状态的后验PDF:

(5)

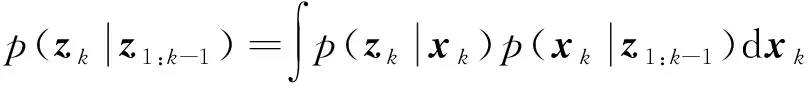
理论上,任何一个复杂的分布函数都可以用多个高斯分布求和的形式进行近似,混合高斯滤波算法正是基于这一原理发展起来的。

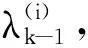
(6)

又设k时刻的过程噪声为包含J个分量的混合高斯分布,即

(7)

根据式(1),k时刻状态转移方程的先验分布为

(8)

由此可得k时刻更新(预测)状态分布为

p(xk|z1:k-1)

(9)

同理,假定k时刻的观测噪声可建模为如下的混合高斯分布形式

(10)

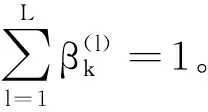
由式(2)可知,k时刻观测方程的似然分布为

(11)

由此可得k时刻测量更新(修正)状态分布为

p(xk|z1:k)

(12)

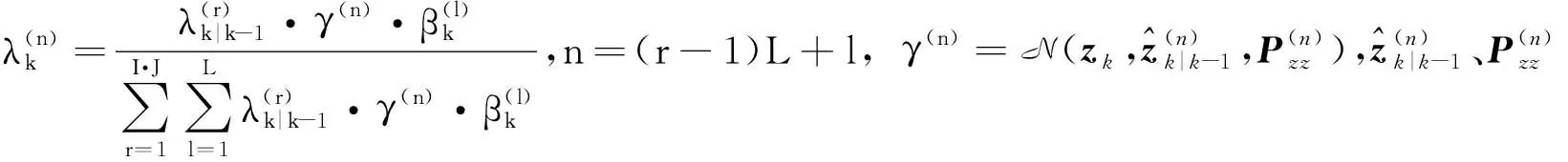
由此可见,经过一步完整的递推过程,高斯分量已由k-1时刻的I个变为k时刻的I·J·L个,随着递推的进行,高斯分量数将爆炸式增长。为此需要在每一步递推完成后,进行剪枝处理,主要是舍弃权值较小的高斯分量,同时对相似性较强(空间距离小)的高斯分量进行合并,具体方法可参考文献[25]。经剪枝后,重新恢复成I个高斯分量,即

(13)

3 交互多模框架下的CKF算法

3.1 闪烁噪声等效建模

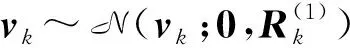
zk=h(xk)+vk(rk)

(14)

式中,rk∈。

由模型条件可知,Pr(rk=M1)=1-ε,Pr(rk=M2)=ε,其中Pr(·)表示概率函数。

假定用πij表示k-1时刻由模式Mi向k时刻模式Mj转移的条件概率,则有

πij≜Pr{rk=Mj|rk-1=Mi}i,j=1,2

(15)

相邻时刻的模式变化关系可用一阶马尔可夫链来描述,其转化关系如图1所示。

图1 常规噪声和闪烁噪声的模式转移关系Fig.1 Mode transition relation of normal noise and glint noise

根据图1中所示的模式转化关系,可得转移概率矩阵为

(16)

需要说明的是,式(16)与传统为机动目标跟踪所设计的转移概率矩阵是不同的,因为后者在主对角线上的元素体现的是下一个时刻保持与当前时刻一致运动模式的概率,因此其取值往往较大[26]。

对于每一个Mi,Mj∈,初始模型概率表示为

(17)

(18)

3.2 交互多模递推框架

考虑由式(1)和式(14)组成的包含多种不同模型的混合系统估计问题,根据全概公式,系统状态的后验PDF为

为表示方便,式中用rk(j)代表rk=Mj。

以各模型为条件的状态后验PDF为

p(xk|rk(j),z1:k-1,zk)

(20)

将全概公式再次用于式(20)中的第二项,则

p(xk|rk(j),z1:k-1)

(21)

在高斯近似假设条件下,式(21)可进一步表示为

p(xk|rk(j),z1:k-1)

(22)

式中,μk-1[i|j]≜Pr(rk-1(i)|rk(j),z1:k-1)称为混合概率。

进一步假定式(22)所示的混合形式为高斯混合分布,而后采用单个高斯分量对其进行矩匹配近似,由此可得

p(xk|rk(j),z1:k-1)

(23)

利用式(23)实现的多模滤波算法称为IMM算法,图2给出了该算法的实现结构,包含2个并行的交互滤波器,混合过程在每个滤波器的输入阶段完成,并以z1:k-1为条件。混合概率的计算将在下文的具体算法流程中详细说明。

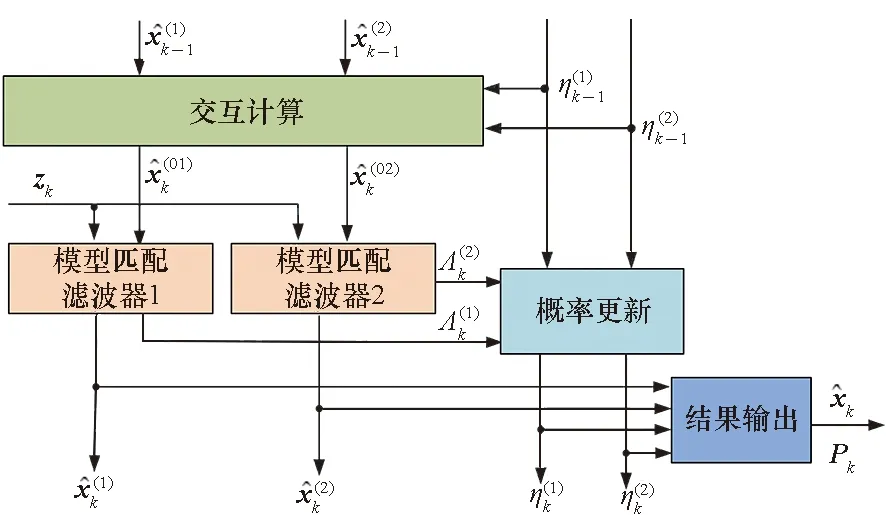
图2 IMM算法框架Fig.2 Framework of IMM algorithm

3.3 基于CKF匹配滤波的算法实现

算法1 交互多模滤波Alg.1 Interacting multiple model filtering

算法2 基于CKF的模型匹配滤波Alg.2 Model-matched filtering based on CKF

需要指出的是,算法1中Step 6只用于结果输出,并不参与递推计算。

4 仿真实验

4.1 仿真条件

(33)

式中:

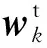
导弹的运动方程为

(34)

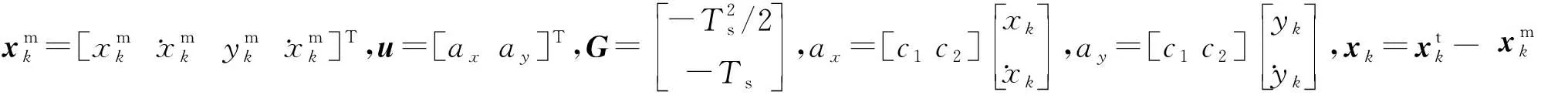
雷达传感器位于弹载观测坐标系的原点,其观测量包括目标的距离和方位角,观测方程的具体形式为

(35)

式中:距离和方位观测噪声vk的分布形式同式(3),闪烁噪声出现的概率为ε。

4.2 仿真结果

仿真中假定目标和导弹的初始状态分别为

图3 导弹拦截目标实验场景Fig.3 Experimental scenario for target intercept

分别采用CKF、高斯混合容积卡尔曼滤波器GM-CKF、标准粒子滤波器(standard PF, SPF)以及本文提出的交互多模容积卡尔曼滤波器IMM-CKF对目标进行跟踪,目标初始状态估计误差的协方差矩阵为

P0=diag[(200 m)2(100 m/s)2(200 m)2(100 m/s)2]

单次实验跟踪结果如图4所示,由此可见,尽管四种算法都能实现对目标的跟踪,但其估计效果各有差异,这一点在图4(b)可以更清楚地看出来;同时不难发现,相较其他几种算法,CKF的误差最大,尤其是在闪烁噪声出现的时刻更加明显。

(a) 原图(a) Original view

(b) 局部放大图(b) Partially zoomed view图4 单次实验跟踪结果示例Fig.4 Target tracking for a single run

为了得到定量化的分析评估结果,对500次Monte Carlo实验结果进行统计,得到目标位置估计的均方根误差(root mean square error,RMSE)如图5所示。

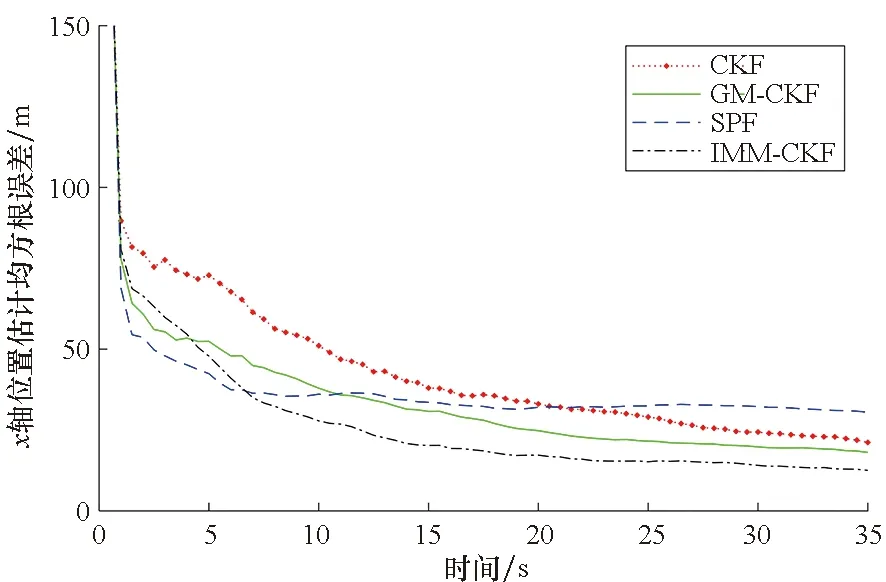
(a) x轴(a) Axis-x

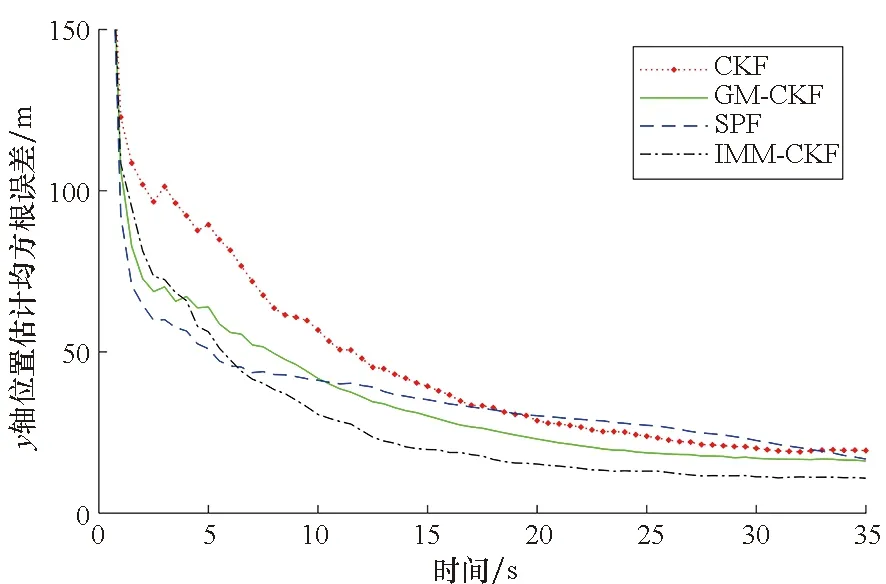
(b) y轴(b) Axis-y图5 目标位置估计均方根误差Fig.5 RMSE for target position estimation

由图5中的结果可以清楚地看出,在存在较大初始误差的情况下,四种跟踪算法经数个周期的递推滤波以后,目标位置估计误差快速下降,并逐渐趋于收敛状态。相比之下,尽管SPF算法在前几个观测周期以最快的速度使估计误差降至一定的范围,但在6 s之后误差下降缓慢(见y轴)或已趋于不变(见x轴),最终的跟踪精度相对偏低;CKF、GM-CKF和IMM-CKF三种算法的跟踪误差虽呈现一致的收敛趋势,但其误差大小各不相同,且渐次减小。整体上,IMM-CKF算法表现出最佳的跟踪效果,这种优势在目标跟踪持续6 s之后更加明显。

为考察不同闪烁噪声对跟踪性能的影响,在前述仿真条件不变的情况下,ε分别取0.05,0.10,0.15,0.20,0.25,0.40,重新开展实验,并对6 s以后各观测周期的均方根误差取均值,得到平均均方根误差(averaged RMSE,ARMSE),如表1所示。表中各个不同ε取值条件下第一行数据对应x轴方向ARMSE,第二行数据对应y轴方向ARMSE。

表1 不同闪烁噪声条件下的位置估计ARMSETab.1 ARMSE for target position estimation with different glint probability 单位:m

由表1可知,随着闪烁概率的增大,四种算法的ARMSE也随之增大;相比之下,IMM-CKF算法的性能最优,且闪烁噪声出现的概率越大,IMM-CKF相对于其他算法的性能增量越明显。

由前文交互多模算法推导过程可知, IMM-CKF除了能跟踪目标状态,还可根据模型概率对闪烁噪声出现与否进行在线估计。图6给出了ε=0.10时,单次仿真中在不同时刻出现真实闪烁噪声的示例,以及由IMM-CKF得到的闪烁噪声出现概率的估计结果。由图6中的结果不难看出,对于大部分真实出现过闪烁噪声的时间点,IMM-CKF也相应呈现较高(或接近1)的闪烁噪声模型概率,说明估计结果与实际情况吻合良好。

图6 闪烁噪声出现时刻估计结果Fig.6 Estimation result for the existence of the glint noise

为定量评估IMM-CKF对闪烁噪声出现时刻的估计性能,表2中给出了不同ε条件下对闪烁噪声出现时刻估计的准确率,其结果通过500次Monte Carlo实验得到。

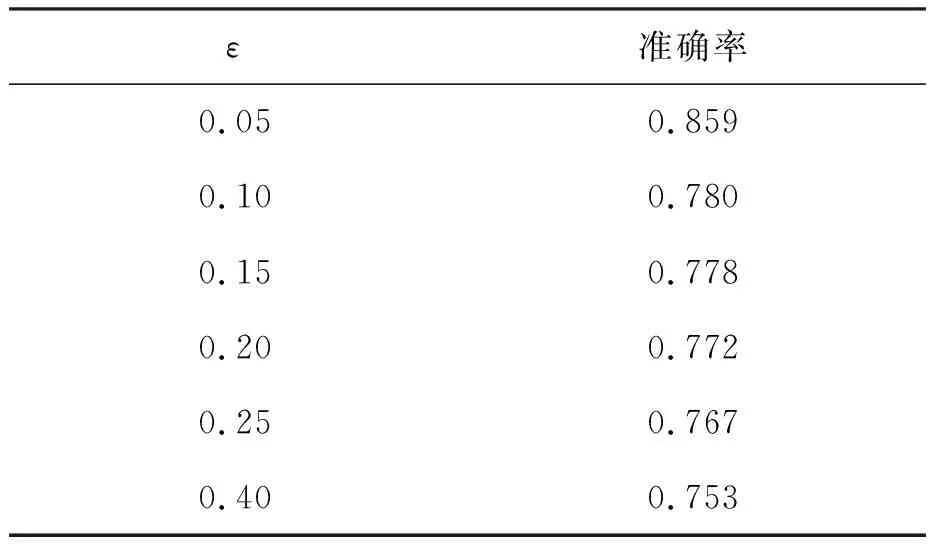
表2 不同仿真条件下对闪烁噪声出现时刻估计的准确率Tab.2 Estimation accuracy for the existence of glint noise under different simulation conditions

由表2可以看出,总体上,所提IMM-CKF能以较高的准确率对闪烁噪声出现的时刻进行估计,这对目标姿态突变检测和干扰判断应用等具有重要的参考价值;同时可以看出,随着闪烁概率的增大,对闪烁噪声出现时刻估计的准确率也有所下降,这与实际情况也是相符的。究其原因,主要是因为滤波算法是通过递推更新的形式实现的,即当前时刻的模式概率估计结果同时受当前时刻量测和前一时刻估计结果的影响。当闪烁概率增大时,模型跳转变得更为频繁,导致短时间内(或瞬时)得到稳定的模型概率估计结果难度增大,从而造成闪烁噪声出现时刻估计精度降低的现象。

表3 四种算法单次仿真运行时间Tab.3 Running time of the four algorithms for a single run

由表3中的结果可以看出,由于CKF算法仅采用了单个高斯分量,因此耗时最少。GM-CKF和IMM-CKF的运行时间分别是CKF的20.61倍和2.19倍,这与GM-CKF采用了20个高斯分量、IMM-CKF采用了2个高斯分量进行近似的实际情况也是完全吻合的。相比之下,SPF耗时最长,且是在粒子并行采样条件下得到的结果。由此可见,IMM-CKF算法复杂度适中,实时性强,非常便于工程实现与应用。

5 结论

闪烁噪声是影响目标跟踪精度的一种重要因素,在制导雷达应用中,如何克服闪烁噪声的影响直接关系到导弹对目标的命中精度和作战效能。本文以闪烁噪声的混合高斯建模为基础,将闪烁噪声发生概率建成一阶马尔可夫模型,并在混合系统理论框架下导出了高斯近似解的表达式,同时通过容积点求解非线性积分方程,从而得到交互多模容积卡尔曼滤波器IMM-CKF。结合典型制导跟踪示例,对所提算法的有效性进行了验证。仿真结果表明,本文算法复杂度仅为传统CKF的2倍,明显低于GM-CKF和SPF算法,且在不同闪烁概率条件下均取得了一致最优的跟踪性能;除此之外,所提算法还能对闪烁噪声出现时刻进行有效的估计,具有很好的实用价值。