异步非平稳干扰抑制方法*

邓 文,黄知涛,2,王 翔,戴定川,陈梁栋

(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 国防科技大学 电子对抗学院, 安徽 合肥 230037; 3. 中国人民解放军95438部队, 四川 眉山 620860)

干扰是合作/非合作通信系统中亟须解决的问题,减轻和抑制干扰对合作/非合作通信系统提升效能具有重要意义[1-2]。在多用户无线通信系统中,发射机通常使用同一媒介将消息发送给相应的接收者,故而每个用户的期望信号之间难以避免相互影响,这导致接收机最终收到的是一种时频混叠观测。接收信号包含期望信号和干扰两种成分,这里的干扰是指除期望信号之外的其他信号成分。现有的干扰抑制工作中,通常假设期望信号和干扰同时到达每个接收者。但实际中各发送节点一般独立工作,同时其工作时长、所发送信号类型以及到达各接收节点的传输时延均可能不同。故在某一接收节点的混叠观测中,不同信号的存在时间区间一般将存在差异(信号在某一时间区间内存在是指其在该区间内具有非零功率)。在本文中,异步非平稳性是指当前干扰信号的数量、种类以及到达接收节点时间动态变化。此外,对干扰抑制技术的研究还应考虑实际系统接收条件,受限于体积、成本等多方面因素,搭载于卫星、飞机等平台的通信系统接收模块大多是单通道。因此,在单通道观测条件下对干扰抑制技术的研究将更具有实际意义。

现有单通道观测条件下干扰抑制的方法主要包括基于广义谱维纳滤波的算法与基于信号子空间投影的算法。前者包括文献[3]中提出的线性共轭线性-频移(linear-conjugate-linear frequency shift, LCL-FRESH)滤波器,其通过对混叠观测的不同频移分量的滤波结果进行加权求和,以在增强目标信号的频移分量成分的同时减弱干扰信号的频移分量成分。但LCL-FRESH滤波器要求已知目标信号循环频率甚至信号波形,这在相当程度上限制了其实用性。为降低FRESH滤波器对训练信号的要求,文献[4]中提出了一种盲自适应FRESH(blind adaptive FRESH, BA-FRESH)滤波器,其直接以混叠观测的某一频移分量取代目标信号本身作为训练信号,因而相较FRESH滤波器而言,实用性显著提升。然而,BA-FRESH滤波器仍要求对目标信号循环频率族的精确先验知识,其性能在循环频率存在误差时将显著下降,同时其在分离性能上较标准的FRESH滤波器存在一定的差距。

除上述基于广义谱维纳滤波的方法外,另一类重要的单信号波形分离技术思路为信号子空间投影。其基本原理为首先构建子空间基底集,使得目标信号与干扰信号在该基底集张成的子空间内尽可能正交,最终通过将混叠观测投影至该信号子空间实现单信号波形分离。针对抗同信道干扰问题,文献[5]提出基于目标信号符号速率信息确定合适的小波基底,随后将混叠观测投影至该小波基底,并基于干扰信号脉冲成型函数先验信息获取干扰信号估计,最终通过将干扰信号估计结果从混叠观测中抵消,实现目标信号波形分离。该方法要求目标信号为基带信号,且目标信号与干扰信号符号速率差异极小,对一般的时频混叠数字通信信号适用性不强。文献[6-7]假设混叠观测中,存在目标信号单信号区域(single signal region, SSR),以SSR检测结果为模板构建目标信号子空间基底,以此减少对目标信号的先验要求。然而,若不存在SSR区域,其性能将显著下降,甚至失效。

此外,与上述基于对目标信号、信道等预先建立的数学模型的算法不同,文献[8]提出了一种直接基于多层深度卷积神经网络(convolutional neural network, CNN)的信号解调器。该方法将单通道混叠观测直接输入解调器,以网络分类层输出作为信号符号序列估计结果,但其易受干扰信号的功率影响,且不能恢复所需信号的波形。因此,在频谱监控、特定信号检测等应用中实用性并不强。

为更好地完成强干扰条件下的信号恢复任务,避免现有干扰抑制算法中存在的不足,本文提出了一种基于数据驱动的稀疏分量分析(sparse component analysis, SCA)干扰抑制方法。基于CNN对数据间强大的建模能力,设计了一个“稀疏域编码-稀疏域表示估计-稀疏域解码”的干扰抑制框架,通过稀疏域编码对时域混叠观测进行稀疏变换。在稀疏域中完成目标信号表示的估计及分离恢复,通过稀疏域解码将稀疏域中的目标信号转换至时域,从而完成目标信号的恢复。与现有基于模型的信号恢复算法不同,本文所提方法基于CNN自适应建立信号恢复模型,突破了对混叠观测先验的限制,实用性更强。

1 异步非平稳干扰信道模型

在多用户通信系统中,由于无线信道的广播特性,接收机除了接收到期望发射机的信息,也会接收到其他发射机的干扰信息,这类通信信道可建模为多用户干扰信道[7,9-10]。这里,考虑包含N对“发送-接收”多用户干扰信道(即其中包含N条主通信链路及N(N-1)条干扰链路),其结构示意如图1所示(实线表示“主通信链路”,指的是某一发射机与其期望的接收机通信形成的链路;虚线表示“干扰链路”,指的是某一接收节点接收与非期望发射机通信形成的链路)。

图1中的每个通信节点均使用单个天线,则在接收节点i(i=1,2,…,N)处的混叠观测可表示为:

vi(n),n∈[1,T]

(1)

式中,aji表示发送节点j(j=1,2,…,N)与接收节点i(i=1,2,…,N)间的信道增益,sj(n-mj)表示传输时延为mj个采样间隔的第j个发送节点所传输的信号,vi(n)表示接收节点i处的加性高斯白噪声(additive white Gaussian noise, AWGN),T为总采样点数。此处考虑各信号传输时延的差异,这主要是由于实际中各目标信号到达接收天线的路径一般不同。具体而言,本文所考虑的数字通信信号si(n)(i=1,2,…,N)可表示为:

(2)

Xi=AiSi+Vi

(3)

式中:Xi∈T×1表示接收节点i处的混叠观测;Ai=[a1i,a2i,…,aji,…,aNi]∈1×N表示混叠矩阵,其中每列表示发送节点j与接收节点i间的信道系数;Si=[s1i,s2i,…,sji,…,sNi]T∈N×T表示信号矩阵,每一行表示接收节点i处收到的发送节点j所传输的信号;Vi∈T×1表示接收节点i处的AWGN。

单天线干扰抑制的目的即实现对Xi中包含的主通信链路成分的波形恢复。图2为混叠观测示意。可以看到,出于对实际应用场景的充分考虑,混叠观测中不存在目标信号SSR。

图2 混叠观测示意Fig.2 Schematics of received signal time-frequency overlapped

2 基于数据驱动的SCA干扰抑制方法

本文干扰抑制方法受基于信号稀疏性假设实现信号分离的SCA技术[11-14]启发。SCA的基本思路为:第一步,对混叠观测进行某种稀疏变换,使目标信号在变换域内具备稀疏性(这是由于在一般应用中,目标信号的稀疏性不能在时域内直接成立)。这里的稀疏性,指的是信号在时域或某一变换域内,仅少数样点取值远离零,而大部分样点取值接近于零。第二步,在变换域内完成混叠矩阵估计。第三步,基于混叠矩阵估计结果,在变换域内完成目标信号的恢复。第四步,通过逆变换将目标信号恢复结果重新转换至时域。从上述基本步骤可以看到,SCA中的三个核心问题为:稀疏变换域的选择、变换域内混叠矩阵的估计及混叠矩阵已知条件下目标信号的恢复。其中,稀疏变换域与信号适配程度决定了信号稀疏性假设的成立程度,即稀疏域中的信号表示基的过完备性决定了后续信号分离的性能。然而,对于通信信号,目前尚未提出具有较好普适性的稀疏变换域,尤其是在单通道观测中包含多个时频混叠信号的情况下。基于此,提出基于数据驱动的SCA干扰抑制方法,以实现目标信号稀疏变换域的自适应选择、变换域内混叠矩阵的自适应学习以及目标信号的自动恢复。本节后续内容将详细介绍所提算法,具体包括干扰抑制方法框架、网络模型设计以及优化目标。

2.1 干扰抑制方法框架

所提干扰抑制方法的框架如图3所示。基于数据驱动的SCA干扰抑制方法包含稀疏域编码、稀疏域表示估计及稀疏域解码三部分。其中,稀疏域编码用于对时域混叠观测进行稀疏变换;稀疏域表示估计用于完成混叠矩阵估计;稀疏域解码用于将目标信号恢复结果重新转换至时域。首先通过稀疏域编码器将混叠观测转换到稀疏空间中的相应的表示;然后用这种表示来估计目标信号在稀疏域中的稀疏表示矩阵,以此实现稀疏空间中目标源信号的恢复;最后通过稀疏域解码器将稀疏域中恢复的目标信号重构为时域上最终的目标信号。

图3 干扰抑制方法框架Fig.3 Schematics of the interference mitigation method

具体而言,本干扰抑制方法的网络框架采用“编码器-分离器-解码器”[15-16]结构。

首先,编码器将时域混叠观测Xi输入转换为稀疏域表示Wi(此处稀疏域是指在该变换域内存在某区域仅目标信号占据主导地位,即仅目标信号具有非零功率),其转换过程定义如下:

Wi=fEncoder(Xi)

(4)

式中,Wi∈K×L为时域混叠混测Xi的深度高维表征,K为编码器滤波器数量,L为单个滤波器的输出长度,fEncoder(·)表示编码器的映射函数。

其次,分离器完成稀疏域中目标信号的表示矩阵Mi∈K×L估计,而后,Mi与Wi相乘得到稀疏域中目标信号的估计K×L,其转换过程定义如下:

(5)

式中,⊗表示矩阵点乘操作。

(6)

其中,fDecoder(·)表示解码器的映射函数。

2.2 网络模型设计

基于数据驱动的SCA干扰抑制方法的网络结构如图4所示,本文干扰抑制算法框架受文献[15]中提出的端到端音频恢复框架ConvTasNet启发,网络模型包括稀疏域编码器、稀疏域表示估计器和稀疏域解码器三个部分,分别对应ConvTasNet中的编码器、分离器和解码器,其中,网络模型的具体实现是基于文献[15]中性能最优情形下的网络结构和参数。

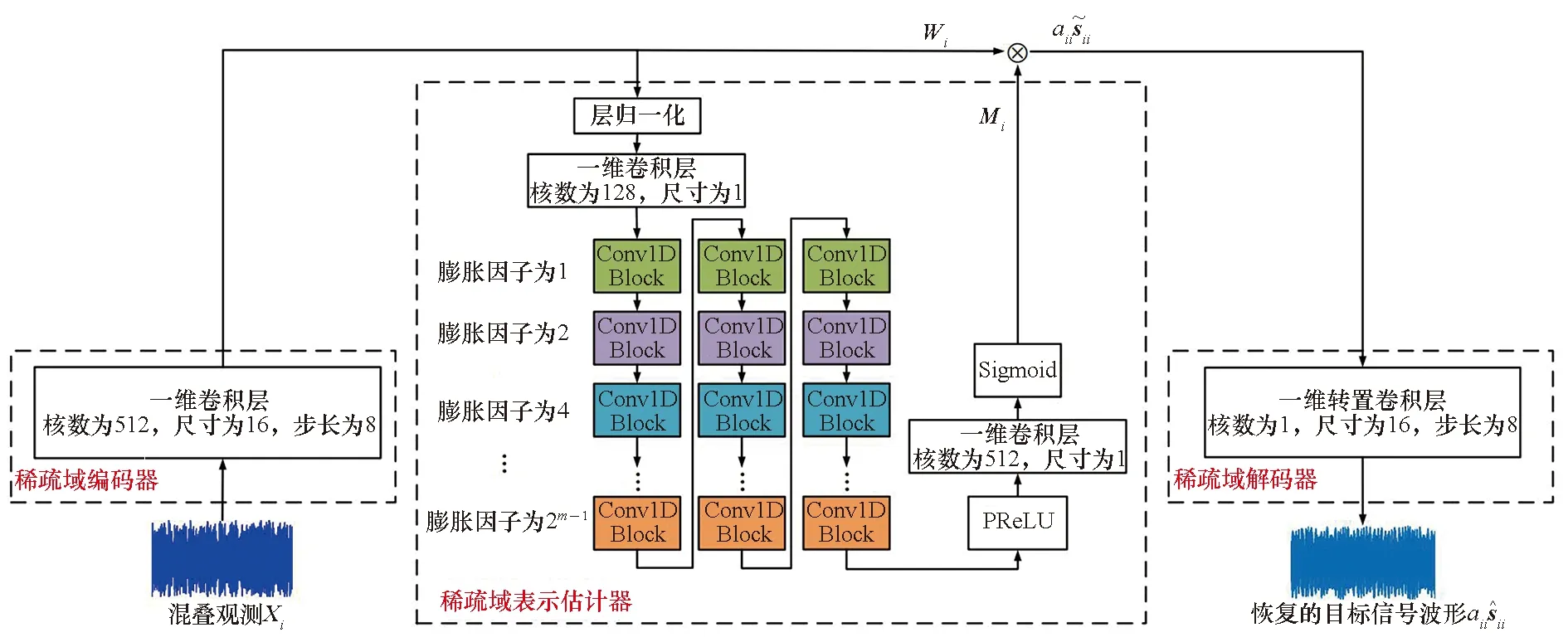
图4 干扰抑制方法网络结构Fig.4 Network structure of the interference mitigation method

1)稀疏域编码器:目标信号稀疏变换域的自适应选择由单个一维卷积层和一个激活函数参数线性修正单元[17](parametric rectified linear unit,PReLU)完成。PReLU定义如下:

(7)

其中,α∈为可训练参数。

2)稀疏域表示估计器:如图4所示,变换域内混叠矩阵的自适应学习主要由三个结构相同的卷积堆叠块完成,其中,前一个卷积堆叠块的输出是后一个卷积堆叠块的输入,设计此结构的目的是通过加深网络深度提取输入的深度表征,而后,卷积堆叠块的输出依次通过一个卷积大小为1的卷积层和一个Sigmoid激活函数,从而完成目标信号在稀疏域中的稀疏表示估计。此外,为减小数据变化对稀疏域表示估计模块稳定性的影响,在稀疏域编码器的输出Wi输入稀疏域表示估计器前,首先要对Wi执行层归一化[18](layer normalization, LN)操作。LN操作之后的卷积层用于控制输入卷积堆叠块的通道数。具体而言,一个卷积堆叠块由8个一维卷积块(Conv1D Block)组成,Conv1D Block结构如图5所示,每个Conv1D Block中的膨胀因子呈指数增长,以此保证网络有足够大的感受野对信号序列长时依赖性建模。其中,第m(m=1,2,…,8)个Conv1D Block中的膨胀因子为2m-1,此外,为减少网络参数量,深度可分离卷积网络[19]被用来替代标准的卷积。LN定义如下:

图5 Conv1D Block结构Fig.5 Structure of Conv1D Block

(8)

(9)

(10)

其中:γ∈K×1和β∈K×1为可训练参数;ε为常量(默认ε=10-5)。

3)稀疏域解码器:目标信号的自动恢复由单个一维转置卷积层完成。

2.3 优化目标

本文所提干扰抑制系统用于恢复目标信号的波形,而评估波形恢复质量的一个很好的标准是估计信号与目标信号之间的相关系数[20],即波形相似度(similarity of waveform, WS),其定义为:

(11)

3 仿真实验及性能分析

本节首先介绍了仿真实验中采用的信号恢复性能衡量指标及主要测试条件指标。随后对本文方法的性能进行了测试,并与现有干扰抑制算法进行了比较。其中,仿真实验1对本文方法在不同环境噪声水平及干扰信号强度下的性能进行了测试,仿真实验2将本文方法与现有算法进行了性能比较,仿真实验3测试了本文方法的泛化性。

3.1 参数设置及性能指标

本文方法的基本训练参数及设置如下:方法模型基于Python 3.8.13/Pytorch 1.11.0/cuda 11.6环境实现,训练、验证、测试数据基于MATLAB R2021a在Intel(R) Core(TM)i7-8700U CPU @3.20 GHz处理器上生成。训练优化器及学习率分别被设置为 Adam 及 0.001,批大小设为10,训练轮数为100。

（1）采用强度等级为32.5＃的普通硅酸盐水泥。水泥的质量应满足GB175—1999《硅酸盐水泥、普通硅酸盐水泥》要求。经过80um筛孔后，水泥的细度不应超过5%。水泥出厂时间不超过2个月。

本小节后续仿真实验中,在对信号恢复性能进行评估时,采用了两类性能指标。一是从目标信号的波形恢复质量角度出发,采用恢复后的目标信号的波形相似度作为性能评估指标,其定义见式(11)。二是从通信传递信息精确度的角度出发,采用恢复后目标信号的解调误符号率(symbol error rate,SER)作为性能评估指标。第i个目标信号对应的SER可定义为:

(12)

由于在对某一目标信号波形进行恢复时,误差主要源自混叠的其他干扰信号及环境噪声的扰动,因而在本节仿真实验中重点考察了本文方法在不同环境噪声水平及干扰信号强度下的性能,并以混叠观测中的信噪比(signal-to-noise ratio, SNR)和信干比(signal-to-interference ratio, SIR)作为扰动强度的衡量指标。对于目标信号i(i∈[1,N]),其在混叠观测中的SNR和SIR被定义为:

(13)

(14)

3.2 仿真实验1

仿真实验1:本文所提干扰抑制方法在不同环境噪声水平及干扰信号强度下的性能测试与分析。

在本实验中考虑N=4的多用户干扰信道中接收节点1处的混叠观测。该混叠观测由目标信号及3个干扰信号组成。目标信号调制样式为BPSK,3个干扰信号调制样式分别为8PSK、PAM8及16QAM。混叠观测采样时长为10 ms,总采样点数为30 720,其中,目标信号存在的时间区间为[0,10]ms,目标信号载频为100 kHz,干扰信号存在的时间区间分别为[0,5]ms、[4,8] ms、[6,10] ms,三个干扰信号的载频分别在[101,103]kHz、[97,99]kHz、[104,106]kHz三个区间随机取值(考虑[-0.5,0.5]kHz的随机载频偏移),混叠观测的频谱示意如图6所示(目标信号载频和三个干扰信号的载频分别为100 kHz,103 kHz,97 kHz,106 kHz)。模型的训练、验证、测试分别基于单个SNR或SIR下的训练、验证、测试样本数分别为6×106、5×105、6×106的样本完成,单个目标信号样本包含320个符号,目标信号与干扰信号的符号速率均为31.25 kBd(Baud)。

表1展示了在不同环境噪声干扰强度SNR下所恢复目标信号的质量,混叠观测中的SIR设置为-4.77 dB。表2展示了在不同干扰信号强度SIR下所恢复目标信号的质量,混叠观测中的SNR设置为20 dB。其中,SERP与SERE分别表示恢复前与恢复后的信号解调误符合率,WSP与WSE分别表示恢复前与恢复后的波形相似度,此处WSP为直接基于混叠观测对目标信号进行计算的波形相似度,SERP为直接基于混叠观测对目标信号进行解调的误符号率。

表1 不同SNR下的SER及WSTab.1 SER and WS under different SNR

从表1可以看到,目标信号的波形得到有效恢复,恢复后波形质量显著提升,在SNR≥5 dB的情况下,WSE等于99.419%。相较于WSP为67.971%而言,提升幅度达到了33.448%,在SNR=0 dB时,提升幅度更是达到了42.3%。从信号解调误符号率的角度而言,可以看到,恢复前由于干扰信号的存在,对目标信号进行解调的SER极高,通信质量极差。经过所提方法恢复后,其SERE得到显著改善。在SNR=0 dB,5 dB时,SERE分别降低至3.749 0×10-3和1.202 2×10-3,相较SERP降低了2个数量级,在SNR≥10 dB的情况下,SER更是降低了3个数量级。

从表2可以看到,在不同干扰信号强度SIR下,所提方法依然能够保证目标信号波形得到高质量的恢复,恢复后目标信号的平均波形相似度达到了99.959%,相较于恢复前平均波形相似度的42.769%,幅度提升了57.19%。从信号解调误符号率的角度出发,可以发现,随着干扰强度的增大,SERE有所增长,但依旧能保持在10-4数量级,相比SERP,平均降低了3个数量级。

本仿真实验结果验证了所提方法在不同环境噪声水平及干扰信号强度下的干扰抑制能力。实验结果表明,所提方法在不同SNR及SIR下,依旧能保持良好的干扰抑制性能。

此外,为测试所提方法对干扰类型变化的适应能力,将干扰信号变为QPSK、PAM4、2FSK,该实验与上述结果相似,在此未重复展示。

3.3 仿真实验2

仿真实验2:本文所提干扰抑制方法与现有干扰抑制算法性能对比分析。

参与比较的现有算法包括:文献[4]中提出的基于稀疏编码及模板匹配的单个信号恢复算法,以及文献[5]中提出的基于字典学习及约束条件下稀疏编码的单个信号恢复算法。在此,所用于对比的算法的参数均与其原文保持一致。其中,文献[5]中的算法的信号特性权重系数设为50。实验数据及参数设置与仿真实验1相同。图7和图8展示不同算法在不同干扰信号强度下的测试WS和SER,其中,WSA和SERA表示文献[4]中方法的性能,WSB和SERB表示文献[5]中方法的性能。

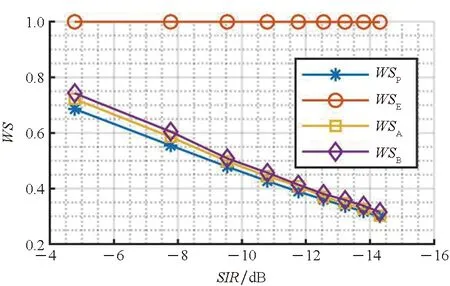
(a) WS

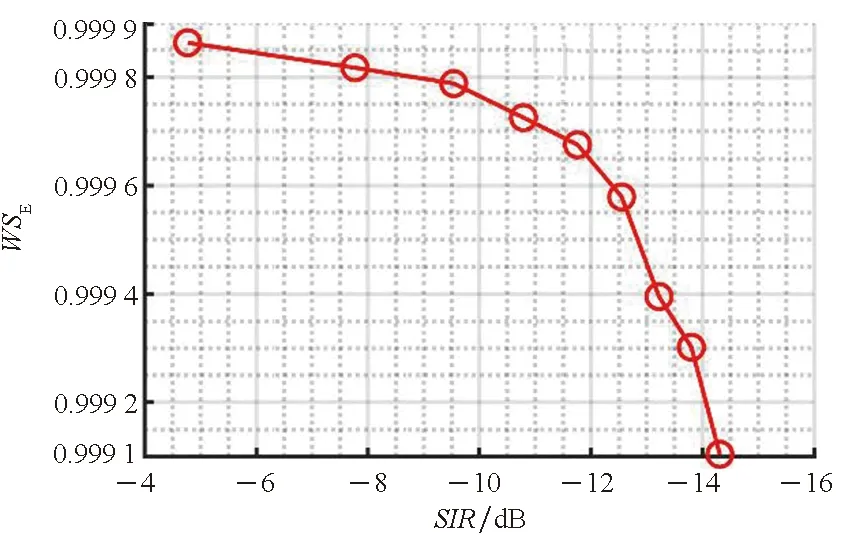
(b) WSE图7 不同SIR下的WSFig.7 WS under different SIR

(a) SER

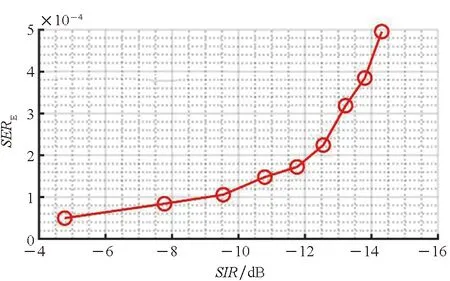
(b) SERE图8 不同SIR下的SERFig.8 SER under different SIR

从图7和图8可以看到,由于文献[4]和文献[5]中的算法是基于存在SSR的假设下提出的,其性能在混叠观测中不存在目标信号SSR时急剧恶化,并随着干扰信号强度的增长,其逐渐失去干扰抑制的能力。主要原因是文献[4]和文献[5]中的算法是基于完全干净的目标信号SSR建立的目标信号子空间基地,若不存在目标信号SSR,其所构建的基地将无法表征目标信号。此外,文献[5]中的算法在干扰信号强度较低时,性能略优于文献[4]中的算法,这是因为文献[5]引入了目标信号的特性作为约束条件,在干扰信号强度较低时,能够提取到部分目标信号的信息,但随着干扰强度的增长,目标信号在混叠观测中的功率将逐渐减小,最终导致算法失效。相比之下,本文所提方法在低SIR场景下依然能够保持稳定的干扰抑制性能。同时,考虑实际中的干扰信号持续时间大都不可控,存在完全干净的SSR可能性较低,本文所提方法所应对的通信场景更贴合现实,应用前景更广。

3.4 仿真实验3

仿真实验3:本文所提干扰抑制方法泛化能力测试与分析。

由于在实际中,干扰信号及信道环境的参数可能是未知且变化的,在此对所提干扰抑制方法应对泛化测试条件的能力进行进一步测试。本实验的训练数据参数与仿真实验1设置相同,而测试数据设置两种改变:一是考虑干扰信号的持续时间不同,3个干扰信号的持续时间设置为[0,4.5]ms、[4,7.5]ms、[5.5,10]ms;二是考虑环境噪声干扰强度的变化改变,初始SNR设置为15 dB。除所述参数改变外,其余参数与仿真实验1中的设置相同。

图9展示了本文所提干扰抑制方法在上述泛化条件下的测试性能,其中,WS1E和SER1E表示在持续时间改变的场景下的测试性能,WS2E和SER2E表示在SNR=15 dB下的测试性能,WS1P、SER1P、WS2P及SER2P分别表示其对应的原始数据直接计算的性能。通过与闭集测试(即测试数据集的参数与训练数据集一致的测试)的结果进行对比可以看到,所提方法模型较好地应对了上述泛化条件。这一优异的泛化能力主要可以归功于构建目标信号稀疏域的方法,其基于数据驱动自适应构建的稀疏域的方式使得目标信号充分稀疏。同时应当指出的是,若在训练时即考虑不同的SNR,则本文所提干扰抑制方法在较低测试SNR下的性能将可以预见地提升。这仅需通过在更广范围的SNR下生成训练数据即可实现。

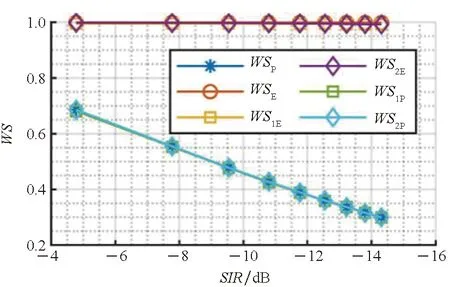
(a) WS

(b) WSE,WS1E,WS2E

(c) SER

(d) SERE,SER1E,SER2E图9 泛化测试条件下的WS和SERFig.9 WS and SER under generalization test conditions

4 结论

本文针对多用户无线通信系统中单通道观测条件下的异步非平稳干扰抑制问题,提出了一种基于数据驱动的SCA干扰抑制方法,利用深度神经网络强大的数据关系建模能力,突破了现有基于模型的算法对混叠观测先验的限制,分别实现了目标信号稀疏变换域的自适应选择、变换域内混叠矩阵的自适应学习以及目标信号的自动恢复。仿真实验结果表明:①所提干扰抑制方法具有在不同干扰类型和干扰强度下高质量恢复目标信号的能力,且对干扰与信号功率水平差异较大的强干扰情况具有很好的适应能力。在不同SNR及SIR下,恢复后平均波形相似度幅度提升了57.19%,误符号率平均降低了3个数量级。②所提基于数据驱动的SCA干扰抑制方法相比现有算法更具普适性,不需要混叠观测的先验要求,能在与干扰时频混叠严重的情况下实现对目标信号的高质量恢复,且适用于单通道接收系统。③所提算法对SNR以及干扰信号持续时间等干扰参数的变化具有较强的适应能力。