聚焦内在关联 实现整体建构——“长方体和正方体的体积”教学思考

王 辉

（浙江省宁波市宁海县城中小学）

“长方体和正方体的体积”是人教版数学教材五年级下册第三单元第三小节的知识，是在学生学习了时间、质量、长度、面积、角度等的基础上，对测量领域的进一步扩充。在测量领域的大观念下，我们要尊重学生的起点，注重体积概念的本质，有结构地教，让学生有关联地学，进而打开学生的思维空间。

一、教材分析

教材安排了体积和体积单位，体积计算公式的推导，体积计算，体积单位间的进率及名数的换算，容积和容积单位，不规则物体的体积等六块内容。

体积对学生来说是一个新概念。教材中对于体积概念的介绍仅停留在物体所占空间的大小，然后马上通过比较两个长方体的体积大小学习体积单位。学习了体积的计算然后又转回到体积单位间的进率及名数的换算。这样的编排，过度强调了体积计算的学习，缺乏体积在测量领域的运用，不利于学生构建有意义的学习序列。

二、学情分析

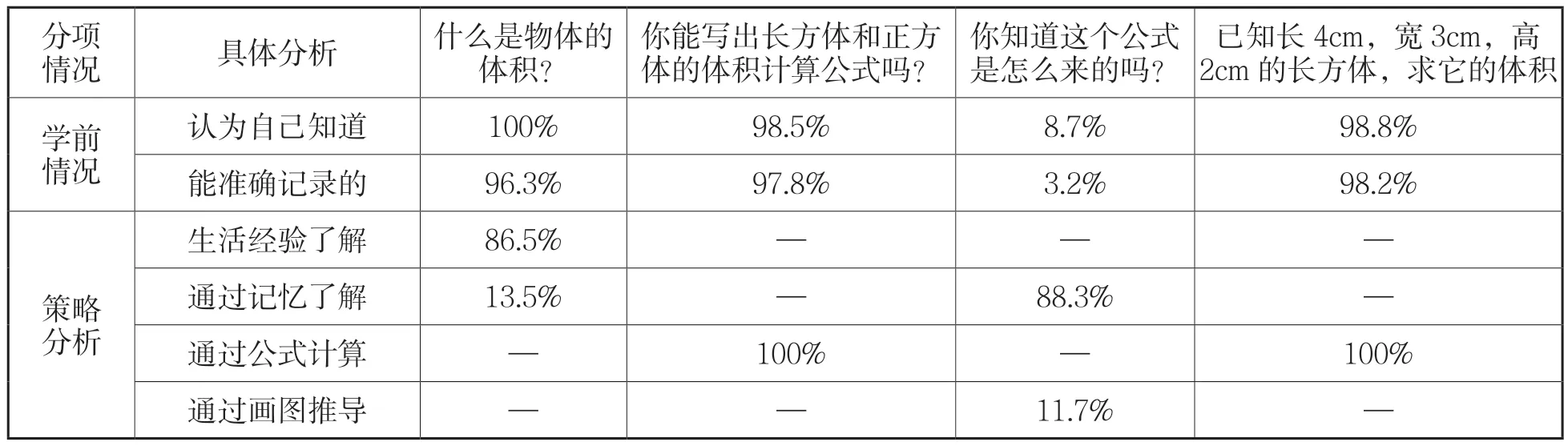
在整合之前，我们除了分析教材，还要研究学情，学生到底是否如我们预想的那样呢？我们通过前测发现，学生对体积的认识仅仅停留在对体积公式的应用上，认为体积是算出来的，而实际上体积是数出来的。我们整理了学生在“长方体和正方体的体积”学习前的学情：

分项情况具体分析什么是物体的体积？你能写出长方体和正方体的体积计算公式吗？你知道这个公式是怎么来的吗？已知长4cm，宽3cm，高2cm的长方体，求它的体积认为自己知道100%98.5%8.7%98.8%能准确记录的96.3%97.8%3.2%98.2%学前情况生活经验了解86.5%——通过记忆了解13.5%—88.3%—通过公式计算—100%—100%通过画图推导——11.7%—策略分析

通过前测，我们发现学生对于体积有了初步的认识。他们认为它是立体的，有一定空间的，是三维的，知道长方体和正方体的体积计算公式。他们的问题在于公式是如何得到的。当然除了这个问题，通过访谈，我们还了解了更多他们想要学习的知识。

从学生的问题中，我们看到学生对体积的学习充满了兴趣和好奇心，但对于体积的认识却比较片面，只会进行简单的体积计算。由此可见，在单元起始课精准地把握起点，让数学与经验对接，贯通包括长度、面积、体积的测量就显得至关重要了。

三、课时划分的重新布局

通过对单元内容的整体分析，基于前测调查学生对于长方体和正方体的体积认识基础上，我们对本节的内容进行了整合和重构。试图在测量的大观念下切入学习，打破学科内容之间的壁垒，体现测量领域知识学习的一致性。体积概念的本质是这个物体（图形）当中包含了相同体积单位的个数。测量体积的大小是用统一体积单位不断累加的过程，数体积单位的个数是测量体积大小的基本方法。从体积的概念到不规则物体的体积，都是体积测量的教学内容。因此，要用体积的概念本质统领体积的所有教学内容。

（一）单元目标的定位

将测量领域的数学大观念在“长方体和正方体的体积”中具体化，就形成了以下的单元目标：

1.理解体积（包括容积）的含义，认识常用的体积度量单位，建立1立方米、1立方分米、1立方厘米以及1毫升、1升的表象，会利用单位间的进率进行简单的换算。

2.探索并掌握长方体、正方体体积的计算方法，并能解决生活中实物体积的测量问题。

3.在具体情境中，经历观察、比较、猜想与验证等活动，丰富学习度量单位的活动经验，感悟一维、二维和三维之间的关联，发展推理意识、量感和空间观念以及培养自主学习和解决问题的能力。

4.体会数学与生活的密切联系，激发学习数学的兴趣。

单元目标集中体现了“长方体和正方体的体积”所学内容的核心、过程中所形成的思想方法及教育价值。

（二）单元课时重新划分

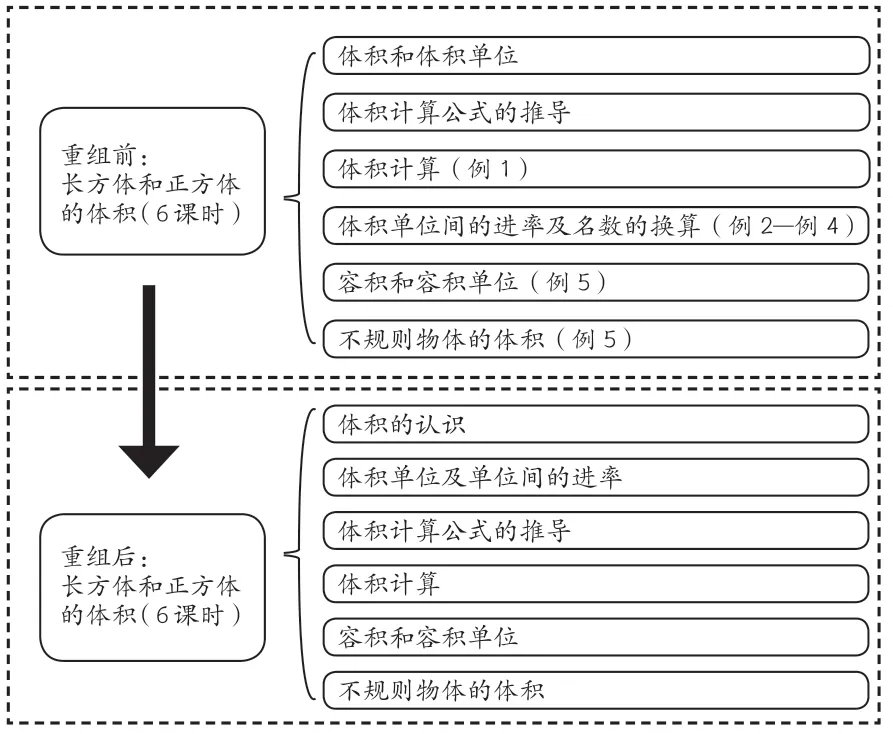
基于以上分析和思考，将本单元的教学内容做适当整合，如下表所示：

四、“体积的认识”课例

（一）教学目标

1.理解体积的含义，会通过数体积单位个数得到体积的大小。

2.在具体情境中，经历观察、比较、猜想与验证等活动，感悟一维、二维和三维之间的关联，发展推理意识、量感和空间观念。

3.体会数学与生活的密切联系，激发学习数学的兴趣。

（二）教学重难点

教学重点：认识体积的概念。

教学难点：感悟一维、二维、三维之间的关联。

（三）教具学具准备

教具准备：课件、书盒。

学具准备：练习纸一张，1立方厘米模型30个。

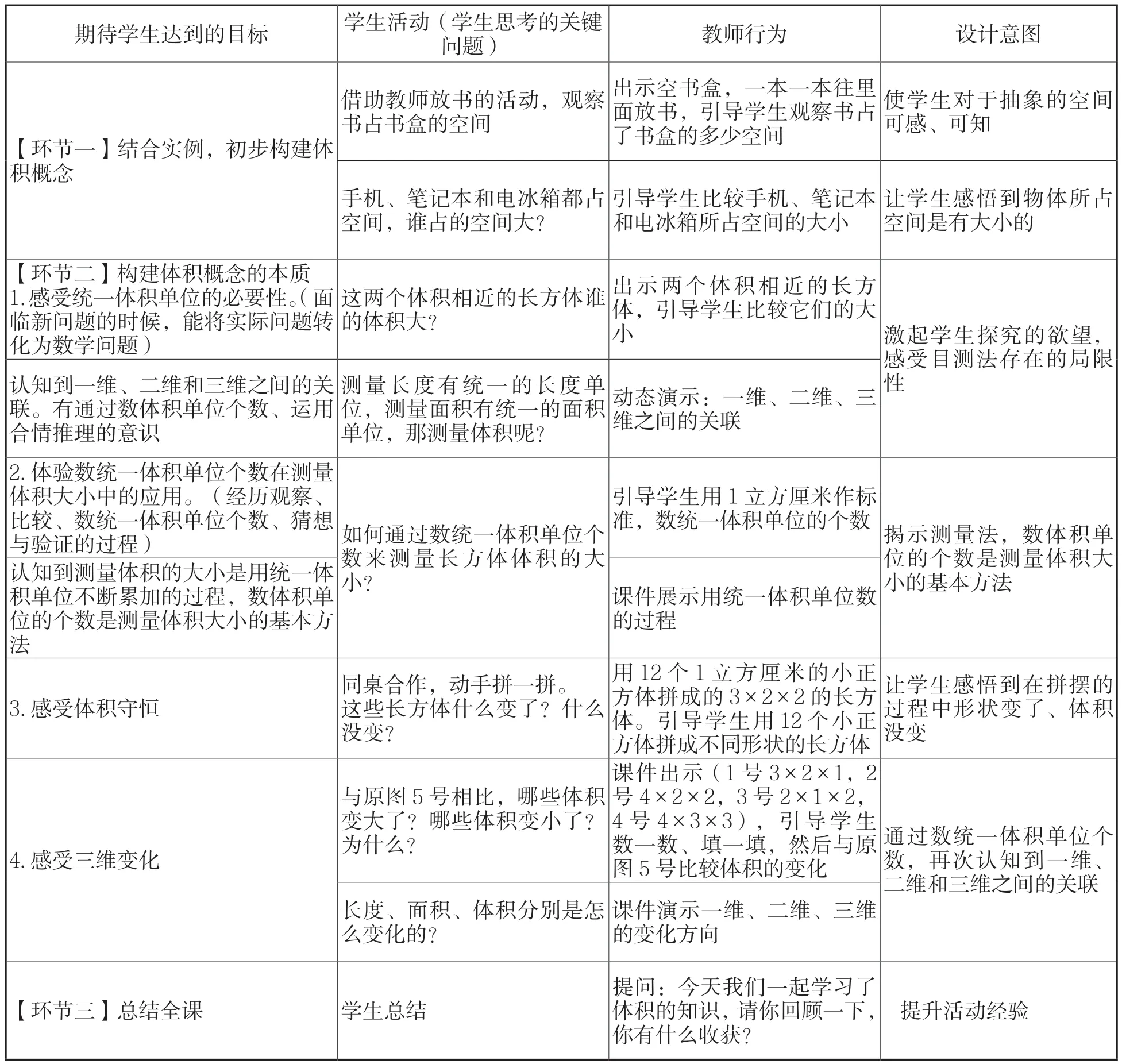
（四）教学流程

期待学生达到的目标学生活动（学生思考的关键问题）教师行为设计意图借助教师放书的活动，观察书占书盒的空间使学生对于抽象的空间可感、可知出示空书盒，一本一本往里面放书，引导学生观察书占了书盒的多少空间【环节一】结合实例，初步构建体积概念手机、笔记本和电冰箱都占空间，谁占的空间大？引导学生比较手机、笔记本和电冰箱所占空间的大小让学生感悟到物体所占空间是有大小的【环节二】构建体积概念的本质1.感受统一体积单位的必要性。（面临新问题的时候，能将实际问题转化为数学问题）这两个体积相近的长方体谁的体积大？出示两个体积相近的长方体，引导学生比较它们的大小认知到一维、二维和三维之间的关联。有通过数体积单位个数、运用合情推理的意识测量长度有统一的长度单位，测量面积有统一的面积单位，那测量体积呢？动态演示：一维、二维、三维之间的关联激起学生探究的欲望，感受目测法存在的局限性2.体验数统一体积单位个数在测量体积大小中的应用。（经历观察、比较、数统一体积单位个数、猜想与验证的过程）如何通过数统一体积单位个数来测量长方体体积的大小？认知到测量体积的大小是用统一体积单位不断累加的过程，数体积单位的个数是测量体积大小的基本方法引导学生用1立方厘米作标准，数统一体积单位的个数揭示测量法，数体积单位的个数是测量体积大小的基本方法课件展示用统一体积单位数的过程3.感受体积守恒同桌合作，动手拼一拼。这些长方体什么变了？什么没变？用12个1立方厘米的小正方体拼成的3×2×2的长方体。引导学生用12个小正方体拼成不同形状的长方体让学生感悟到在拼摆的过程中形状变了、体积没变4.感受三维变化与原图5号相比，哪些体积变大了？哪些体积变小了？为什么？通过数统一体积单位个数，再次认知到一维、二维和三维之间的关联长度、面积、体积分别是怎么变化的？课件出示（1号3×2×1，2号4×2×2，3号2×1×2，4号4×3×3），引导学生数一数、填一填，然后与原图5号比较体积的变化课件演示一维、二维、三维的变化方向【环节三】总结全课学生总结提问：今天我们一起学习了体积的知识，请你回顾一下，你有什么收获？提升活动经验

总之，通过大观念下的单元整体教学设计，“长方体和正方体的体积”教得深刻、有厚度，很好地培养了学生的数学素养和空间观念。基于大观念的单元整体教学能够帮助学生理解，促使他们在今后的学习中主动迁移，最终学会学习。而如何进一步研究“大观念下的单元整体教学设计”，如何进一步将核心素养落到实处，值得我不断深思，不断努力。