考虑节点相互影响的公交网络节点重要性识别算法

钟志敏，姜仙童，田秀珠，王 昌

（1.交科院技术咨询（北京）有限公司，北京 100029；2.交通运输部科学研究院，北京 100029）

0 引言

《国务院关于印发“十四五”现代综合交通运输体系发展规划的通知》（国发〔2021〕27号）[1]指出，要提高交通网络抗风险能力，增强交通运输网络韧性。其中，城市公交网络的抗风险性、可靠性是两个重要方面。在城市公交网络中，重要公交站点对维持网络的结构完善和功能正常运转有着重要的作用，因此准确识别公交网络的重要站点，进而采取适当的管控措施优化站点的通行条件和服务能力，对增强城市公交网络稳定性，保障公交安全高效运营具有重要意义。

重要节点是指对网络结构或功能具有较大影响的节点，识别复杂网络重要节点是当前的研究热点。经典的节点重要性算法有度中心性[2]、半局部中心性[3]、介数中心性[4]、紧密度中心性[5]、k-壳分解法[6]等。有些学者在此基础上进行了优化，如王清晨[7]、任卓明等[8]、阮逸润等[9]、胡钢等[10]、Xu 等[11]、朱敬成等[12]用度、集聚系数、拓扑重合度等拓扑特性描述节点和邻居节点间的联系，提出各自的节点重要性算法，但只考虑了网络的局部结构。部分学者提出的算法综合考虑了网络的局部结构和全局结构，对重要节点的识别具有不错的效果，如Yang 等[13]、Li 等[14]结合邻居节点信息和路径信息，分别提出基于重力中心性的k 壳算法（K-shell Based on Gravity Centrality,KSGC）、基于度和k 壳的重力模型算法（DKBased Gravity Model,DKGM）算法；卢鹏丽等[15]结合节点的介数中心性和邻居节点的度中心性，提出用介度熵来衡量节点重要性；Ullah 等[16]提出考虑节点自身影响和全局影响的全局结构模型（Global Structure Model,GSM）算法；刘书磊等[17]和周漩等[18]考虑了边对节点的影响，但仅关注边的局部信息，未考虑边对网络全局的影响。

当前，对节点与邻居节点互相影响的节点重要性算法研究中，更多地关注网络的局部结构，较少研究节点连边对两端节点的影响，也忽视了网络的全局特征。同时，研究也更多聚焦在使用SIS/SIR（Susceptible-Infectious-Susceptible/Susceptible-Infectious-Recovered）等网络模型对各种算法进行效果评估，较少使用真实复杂系统验证算法有效性，易忽略不同真实复杂系统之间的差异。因此，在考虑网络局部特征、全局特征和节点间相互影响的节点重要性算法的基础上，为准确识别公交网络中的重要站点，以增强网络的连通性和可靠性，保障乘客顺利出行，本文提出一种基于复杂网络的节点度、邻居节点度、边介数和节点间客流的算法——DeB（Degree and edge Betweenness），并以真实的公交网络为例进行仿真分析，验证算法性能，以期准确有效地识别公交网络的重要站点，增强网络的连通性和韧性，提升网络的可靠性。

1 复杂网络基础理论

近年来，因城镇化发展和城市规模扩张，城市公交系统规模不断扩大，逐渐变成一个复杂巨系统，由此引发一系列难题。复杂网络理论因而被用于城市公交网络相关研究中。复杂网络中存在一些特殊的节点被称为重要节点，其受到攻击不能正常发挥作用时，整个复杂网络可能会受到较大的影响，因此节点重要性识别研究是复杂网络领域的重要研究方向。

复杂网络的数学表现形式为节点构成的集合V和连边构成的集合E组成的图G=(V,E)，网络节点数量N=|V|，连边数量M=|E|。

1.1 重要节点识别方法

1.1.1 节点度和度中心性

节点度ki表示与节点i直接连通的节点的数量，即网络中以节点i为端点的边的数量[2]，其计算公式为：

式（1）中：eij为节点i与节点j之间的边。

其中，若节点i与节点j有直接相连的边，则eij=1，反之eij=0。

度中心性D(i) 认为网络中与节点相连的节点越多，则该节点在网络中越重要。节点i的度中心性定义为节点i的度与该节点可能存在最大连边数量的比值[2]，其计算公式为：

式（2）中：N为网络中节点的数量。

度中心性是最早用于识别重要节点的算法，具有计算速度较快、应用范围较广的优势，但其仅关注网络的局部特征，具有较大的片面性。

1.1.2 节点介数和介数中心性

介数Bi表示网络中经过节点i的最短路径的数量与网络中所有最短路径数量总和的比值[4]，其计算公式为：

式（3）中：njk为节点对j、k间的最短路径数量；njk(i)为节点对j、k之间的最短路径中通过节点i的最短路径数量。

介数中心性B(i)认为网络中所有节点对的最短路径中经过节点i的次数越多，节点越重要[4]。对无向网络来说，B(i)计算公式为：

介数中心性考虑了节点之间的最短路径，节点介数越高，表明途经该节点的最短路径越多、节点的重要性越高，是容易造成网络拥堵的瓶颈点。

1.2 网络建模方法

复杂网络由节点和边组成，网络建模是将现实网络抽象成适合进行复杂网络分析的过程。本文针对公交网络进行建模，与其他建模方法相比，L空间法更能体现公交网络站点与站点之间、站点与线路之间的拓扑关系，侧重于公交基础设施的连接，反映网络自然连接的状态，便于分析网络最基本的特征和形态。因此，本文采用L 空间法，将公交网络构造成由站点和线路构成的复杂网络，考虑站点间的连接情况和客流情况，将公交系统中的站点当作网络节点，站点间的关系当作节点的连边。按照以下原则构建无向加权复杂公交网络。

1）公交停靠站点为网络节点，若两站点是某条线路中相邻的停靠站，则两节点间有边相连，否则两节点不相连；两节点之间至多只能存在一条边。

2）名称相同的站点视为同一节点，若站点有多个分站，也视为同一节点；名称不同的两个站点即使距离很近，也视为不同节点。

3）环形线路以内环线的停靠站点为准；支线与主线视为两条线路；上行线路与下行线路走向不一致时，以上行线路的停靠站点为准。

4）节点间连边的权重为途经节点的客流情况。

2 DeB节点重要性识别算法

2.1 算法原理

现实公交网络中，相邻的两个公交站点之间往往相距不远，特别是在城市中心区域，干线和支线公交线路的平均站距一般分别为0.5～0.8 km和0.3～0.5 km[19]，因此经常出现乘客在搭乘同方向公交线路时，在不同公交站点上、下车的现象。如图1 所示，出行起点S 到公交站点A 和B、出行终点T 到公交站点C 和D 的距离相差很少，因此从出行起点S到出行终点T之间可能存在4条出行路径，即S→A→C→T、S→B→C→T、S→A→D→T、S→B→D→T。

图1 公交出行上下车站点选择及其出行路径

站点的距离越近，各条路径出行时间相差不大的可能性越大，站点间客流的相互影响也越大。该影响力的大小与途经站点的线路数量、发车间隔、客流大小有关，也与站点之间的路径在整个网络中的位置有关。由此，本文认为在复杂公交网络中，节点的重要性不仅与节点及其邻居节点的度值有关，也与该节点及其邻居节点间的相互影响有关。鉴于此，本文提出基于节点度、邻居节点度、边介数和节点间客流的DeB 重要节点识别算法，边介数和节点间客流是连边的重要属性，也分别作为网络拓扑结构特征和网络运营特征，在DeB 算法中表现为节点连边对两端节点影响力的大小。

同节点介数一样，边介数Beij是指网络中所有节点对的最短路径中经过边eij的数量占最短路径总数的比例[4]，其计算公式为：

式（5）中：nkl为节点对k,l间最短路径的数量；nkl(ij)为节点对k,l间最短路径中通过边eij的最短路径数量。

由边介数的定义可知，Beij越大，表示途经边eij的最短路径越多，边eij两端的节点i和节点j相互之间的影响越大。

为描述DeB 算法下节点的重要性，引入节点吸引度Ai指标，定义节点i的吸引度Ai为节点i向其邻居节点吸收的度值与其自身度值之和。吸引度Ai计算公式为：

式（6）中：Γi为节点i的邻居节点集合；pij为途经节点对i、j间的客流。

更进一步，考虑到邻居节点对其邻居节点也会产生吸引，因此定义节点i的n阶吸引度为节点向其邻居节点吸收n次之后的节点重要性指标，其计算公式为：

式（7）中：n≥1，且=ki，即节点i的0 阶吸引度等于其节点度。

2.2 算法有效性评价指标

通过节点重要性算法获得节点重要性序列后，需进一步验证算法的有效性。验证方法是：按节点重要性排序在所获得的节点序列中依次移除节点，即基于节点重要性算法的蓄意攻击，观察节点移除过程中网络结构和功能的变化情况。网络效率和最大连通子图是常用的评价网络结构或功能的指标。在公交网络中，网络效率表现为乘客通过公交出行到达网络中其他节点的难易程度，即网络效率越高，乘客公交出行越方便；最大连通子图表现为乘客通过公交出行可到达网络中其他节点的能力，即最大连通子图越大，乘客可到达目的地的概率越大。

1）网络效率和累积网络效率

网络效率E[20]是指网络中所有节点对距离倒数之和的平均值，计算公式为：

式（8）中：dij为节点对i、j间的最短距离。

其中，若节点对i、j之间不存在最短路径，则1/dij=0。对于加权网络，式（8）中的dij可替换为边权wij，即考虑了边权wij的网络效率。

累积网络效率Ec[21]是指节点移除的过程中，得到的所有网络效率之和，其计算公式为：

式（9）中：m为已移除的节点的集合。

按照不同序列移除节点所得到的Ec不同，Ec越小表示该序列对网络效率的影响越大。

2）最大连通子图和累积最大连通子图

最大连通子图是体现网络连通性的度量指标，连通图的最大连通子图就是其本身，非连通图的最大连通子图是指连接节点数量最多的连通子图[22]。节点移除后，连通图可能变成非连通图，并形成多个节点数量不同的连通子图，最大连通子图的规模Nmax越大，其最大限度保持正常通行的能力就越强。Nmax计算公式为：

式（10）中：Nmax为最大连通子图规模，即最大连通子图包含的节点数量；N1,N2,N3…为各连通子图包含的节点数目。

2.3 算例分析

为验证DeB 算法的有效性，本节以图2 所示的算例网络为例，研究分析DeB 算法与度中心性、介数中心性两种算法在节点删除时网络结构和功能的变化。假设图2中节点间客流均为1，即算例网络为无权网络。因算例网络的直径为6，故将DeB 算法得到的1 阶吸引度、2 阶吸引度和6阶吸引度与度中心性、介数中心性相比较，重要节点序列如表1所示。

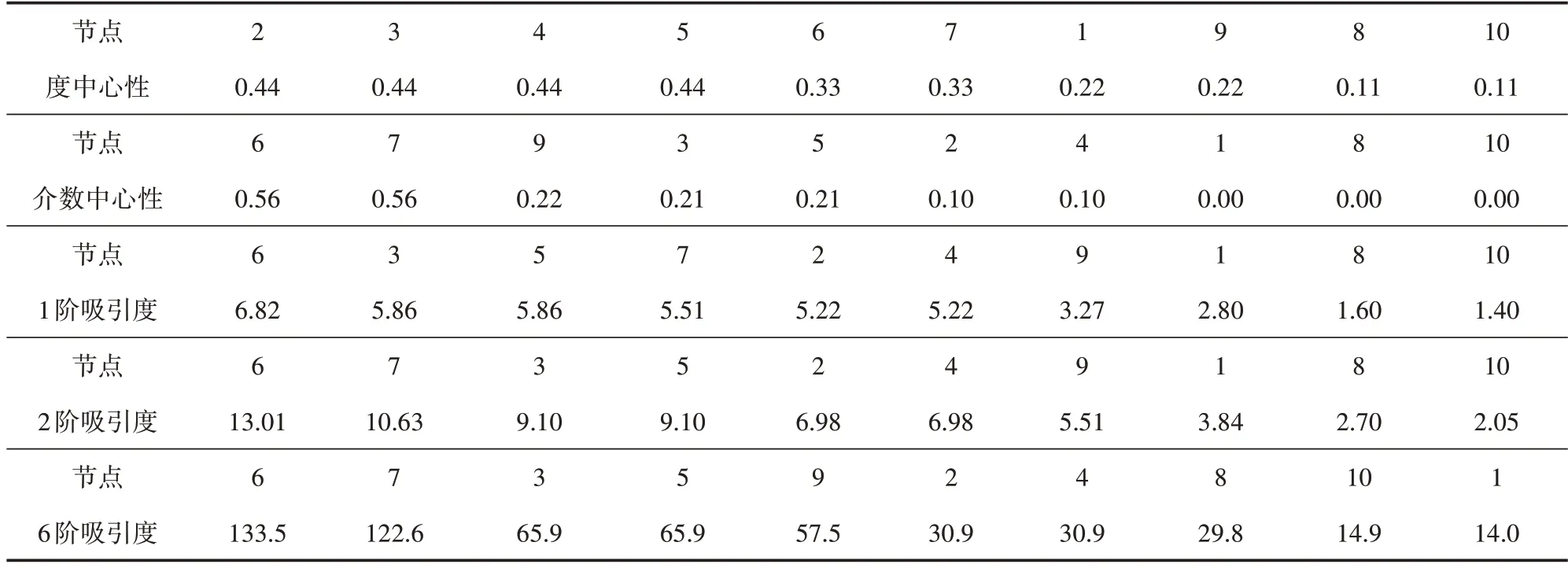
表1 算例网络的重要节点序列

图2 算例网络拓扑结构图

由图2 和表1 可知，节点6、7 是“桥节点”，只要移除其中一个，网络将变成非连通图。介数中心性认为节点6、7是最重要的节点，介数均为0.56，DeB 算法认为节点6 的重要性较节点7 更高，这符合节点6 的一侧较节点7 连接了更多的节点，重要性应较节点7更高的现象；节点2、3、4、5 的度中心性均为0.44，节点8、10 的度中心性均为0.11，但节点3、5 更靠近网络的中心位置，因此其介数中心性更高，在DeB 算法中，其吸引度也比节点2、4、10 更高；节点1、9 的度中心性均为0.22，但节点9 是到达节点10的必经之路，其各阶吸引度也都比节点1的更高。由此可知，当网络为无权网络时，采用吸引度衡量节点重要性的DeB算法可有效识别出重要节点。

DeB 算法得到不同阶数的节点吸引度不同，其节点重要性排序也不同，当阶数n=6 时，节点9 的吸引度比节点2 和节点4 的高，节点8 与节点2 和4 的吸引度相接近，这与节点移除后对网络结构和功能的影响表现不一致（见图3）。因此，为提高DeB 算法对重要节点识别的准确性，需针对不同的网络确定节点吸引度最佳阶数。

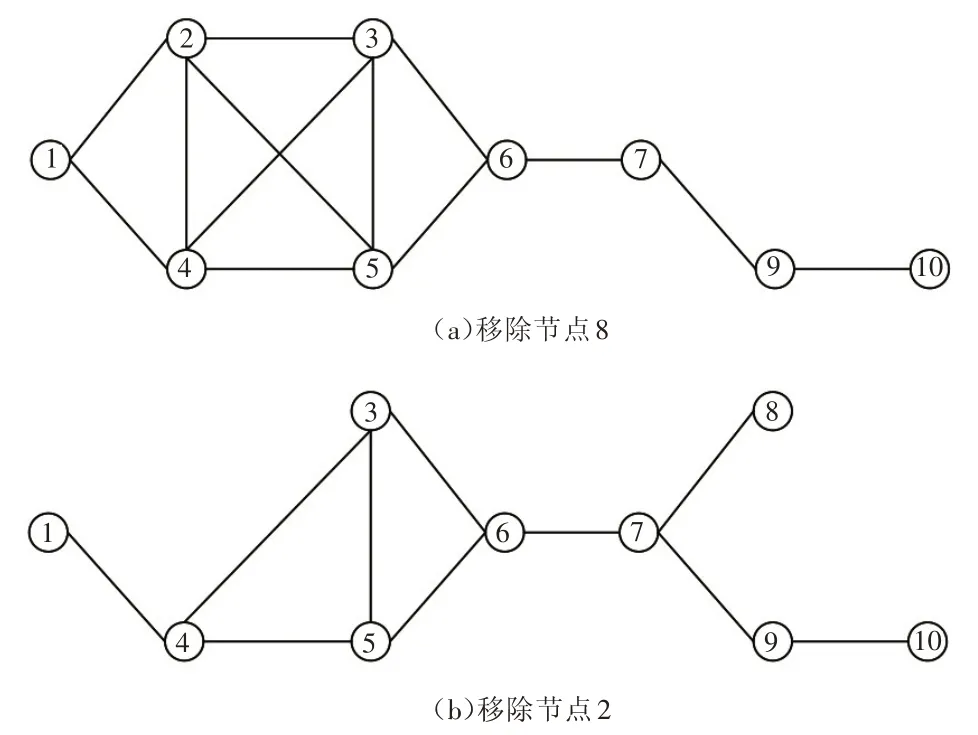
图3 移除节点8或节点2后算例网络拓扑结构图

3 实证分析

本文以宁波市公交系统为例，按照上文描述的建模方法构建无向加权的复杂公交网络。网络包含1 531 个节点、2 231 条边，平均节点度为2.91，平均最短距离为17.06站。

3.1 节点吸引度最佳阶数

节点i的n阶吸引度，是n-1 阶吸引度与节点通过连边的边介数向其邻居节点中吸引而来的吸收值之和。该吸收值与边介数、邻居节点的n-1 阶吸引度有关，而邻居节点的n-1 阶吸引度与其邻居节点的n-2 阶吸引度有关，由此推之，当n达到一定值时，节点吸引度将遍历网络中所有节点。

由本文第2 节的研究可知，节点吸引度的阶数将影响DeB 算法的有效性，考虑到本文研究的宁波市公交网络的平均最短距离为17.06 站，故本文的研究对象为节点的1～9阶吸引度。

本文通过对公交网络进行模拟蓄意攻击，观察网络效率和最大连通子图的变化情况以确定最佳吸引度阶数。公交网络的节点数量较大，若逐一移除节点，数据处理时间会较长，因此采取每次移除0.05N个节点数量，即前19 次每次移除77个节点，最后1次移除68个节点，分20次将节点完全移除的蓄意攻击策略。

图4 所示为1～9 阶吸引度对网络效率和最大连通子图的影响，图中的横坐标为节点移除比例，纵坐标为节点移除后的网络效率和最大连通子图规模。表2 给出了1～9 阶吸引度下累积网络效率和累积最大连通子图规模的数据。

表2 1～9阶吸引度下累积网络效率和累积最大连通子图规模数据

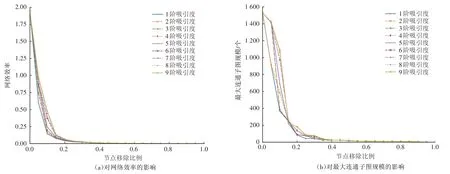
图4 1～9阶吸引度对网络效率和最大连通子图的影响

由图4 可知，不管是网络效率还是最大连通子图规模，1 阶吸引度的曲线在大部分时间内处于图的最下方，表2 中1 阶吸引度的累积网络效率和累积最大连通子图规模也低于其余阶数吸引度，且累积网络效率和累积最大连通子图规模随节点吸引度阶数的增加而呈上升趋势。换言之，与其他阶数的吸引度相比，1 阶吸引度能更好地衡量公交复杂网络节点的重要性。

3.2 DeB算法验证

由于DeB 算法获得的1 阶吸引度对重要节点识别的准确性最高，因此研究比较网络效率和最大连通子图规模在基于1 阶吸引度、度中心性、介数中心性三种蓄意攻击策略下的变化情况，以验证DeB算法的准确性。

1）网络效率

采取每次移除0.05N个节点，直至全部节点被移除的蓄意攻击策略，移除节点的比例和网络效率之间的关系如图5 所示。在1 阶吸引度、度中心性、介数中心性3种蓄意攻击策略下，1阶吸引度的网络效率下降最快，介数中心性下降相对缓和，度中心性介于二者之间。

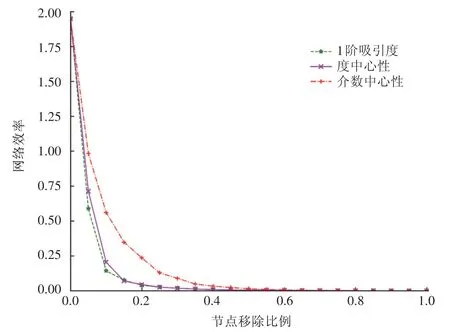
图5 每次移除0.05N个节点对网络效率的影响

当节点移除比例低于0.2 时，网络效率下降速率较快，尤其是移除了前0.05N个节点时，3种算法的网络效率下降幅度均最大。随着移除比例的增加，网络效率的下降幅度变小，体现了重要节点对网络效率的影响比其他节点大。当节点移除比例达到0.2N后，3 种算法下的网络效率均低于0.1。

为进一步分析重要节点对网络效率的影响，本文还采取了第2种蓄意攻击策略，即每次移除1个节点，直至0.2N个节点被移除。该种攻击策略下，网络效率的变化情况如图6所示。

图6 每次移除1个节点直至0.2N个节点被移除对网络效率的影响

由图6 可知，移除前2 个节点时，介数中心性的网络效率下降最快，然后1 阶吸引度的网络效率下降幅度超过了介数中心性，之后在部分区域与度中心性的网络效率下降幅度相差不大，但是多数情况下1阶吸引度的曲线处于图的最下方，网络效率下降幅度最大。

经测算，在节点移除比例由0.05 增大到1 的过程中，1 阶吸引度的累积网络效率均比其他两种算法小，其次是度中心性，最大的是介数中心性，如表3所示。

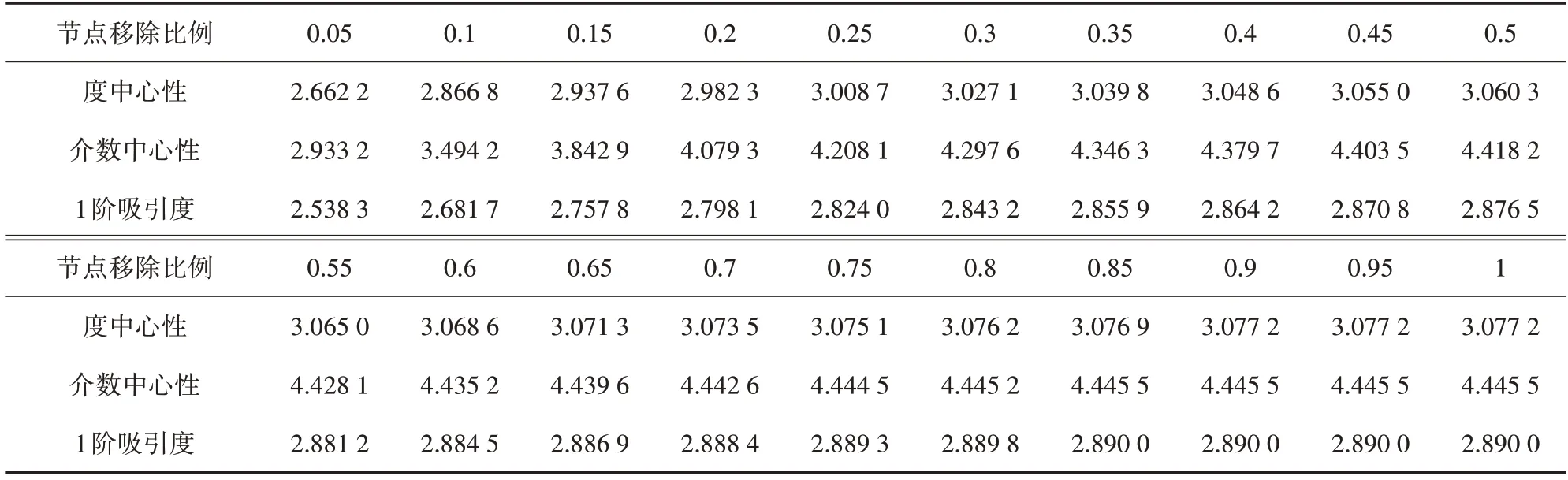
表3 不同节点移除比例对应的累积网络效率

2）最大连通子图规模

与网络效率一样，分别采取两种蓄意攻击策略研究移除节点比例和最大连通子图规模之间的关系，详见图7和图8。

图7 每次移除0.05N个节点直至节点全部移除对最大连通子图规模的影响

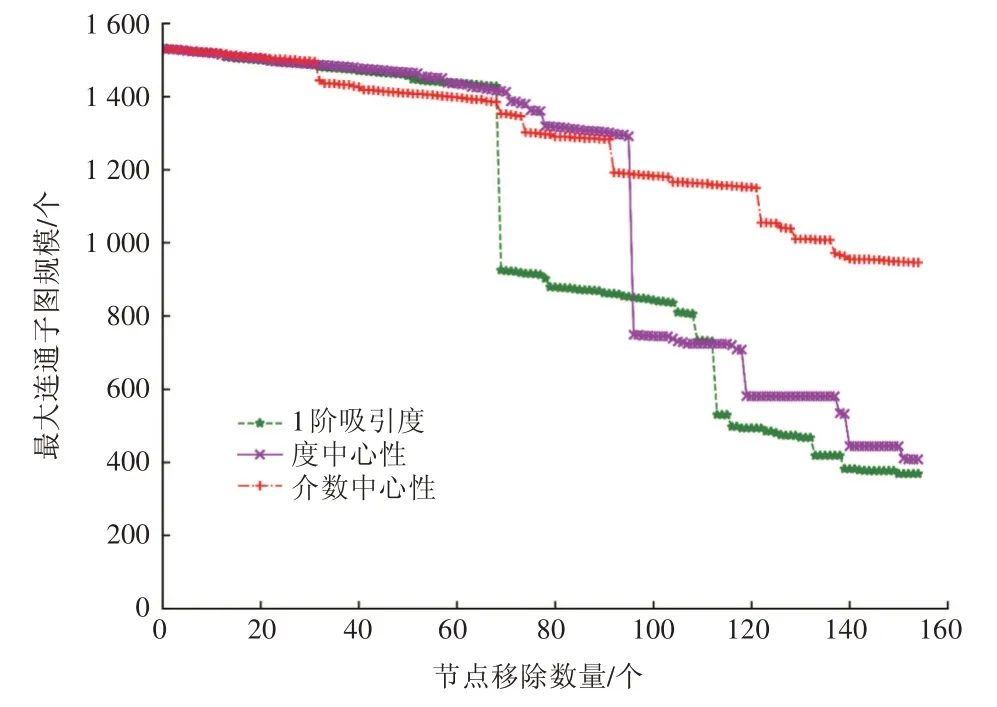
图8 每次移除1个节点直至0.2N个节点被移除对最大连通子图规模的影响

由图7 和图8 可以看出，与移除节点对网络效率的影响一致，大多数情况下1 阶吸引度的曲线都处于图的最下方，即其最大连通子图规模变化最大，网络的连通性最差。其中，图8 中3 种算法均呈现最大连通子图规模缓慢下降和突然下降交替出现的现象，即多数情况下，每移除1 个节点，最大连通子图规模相应地减少1 个，曲线下降较为缓慢，直至被移除的节点累积到一定的数量时，最大连通子图的规模出现断崖式下降，随后又恢复成缓慢下降的状态。移除的节点重要性越高，最大连通子图出现断崖式下降的频率也越快，体现了重要节点对最大连通子图的影响更大，少部分重要节点的移除会对网络的连通性产生严重的影响。

经测算，在节点移除比例由0.05 增大到1 的过程中，1 阶吸引度的累积最大连通子图规模均比其他两种算法小，其次是度中心性，最大的是介数中心性（见表4），这与节点移除对网络效率的影响相似。

表4 不同节点移除比例对应的累积最大连通子图规模 单位：个

以宁波市公交系统排名靠前的节点为例，进一步比较分析节点1 阶吸引度与度中心性和介数中心性对重要节点的识别情况，表5 仅列举了3种节点重要性识别算法获取的重要性排名前20的节点情况。研究结果表明，节点1 阶吸引度是在度中心性基础上进行优化，因此其得到的节点重要性排序与度中心性的相似度最高，前20个节点中有13个相同的节点，但是排序大不相同，且距离越靠后，排序的差别越大。不同的7个节点中，宁大附属医院、红梅新村、镇海公交、白沙路、外滩等5 个站点位于介数中心性前20，孔浦中学位于介数中心性的第31，陆家村分别位于度中心性和介数中心性的第25和53。这也说明DeB算法所获得的1 阶吸引度融合了度中心性算法和介数中心性算法二者的特性，实现了二者的优势互补，可以识别出度中心性和介数中心性各自所忽视的部分节点的重要性。

表5 3种算法识别的重要性前20节点对比

3.3 算法性能总结

综合来看，相较于度中心性和介数中心性，1 阶吸引度能更准确地识别网络中的重要节点。DeB 算法获得的1 阶吸引度融合了度中心性算法和介数中心性算法分别体现出的网络局部特征和全局特征，以及客流所体现出的网络现实特征，在宁波市公交网络重要节点识别中表现出较好的准确性。此外，本方法还应用于青岛市、株洲市等城市，为当地公交网络运营提供了有价值的参考，进一步验证了算法的普适性与可移植性。

4 结束语

准确识别重要公交站点，采取适当措施优化重要站点周边的道路交通条件，对提高公交网络运营的稳定性和韧性具有重要的现实意义。本文聚焦于连边对重要节点的影响，采用边介数和客流两项指标，从网络拓扑结构和网络实际运行状态两个方面描述连边对两端节点的影响，进而提出了DeB 重要节点识别算法。在此基础上，通过对宁波市等城市公交网络的实证研究，发现该算法的节点1 阶吸引度能较好地衡量公交站点的重要性。本文研究成果可为公交网络运营、客流应急疏散等提供一定的参考。

本文是基于无向加权公交网络的研究，仅考虑了公交网络客流对重要节点的影响，对真实公交网络的刻画精确度有待提升。下一步，将根据公交发车间隔、公交运行里程和时间、乘客换乘情况等实际运营情况构建更加真实的公交网络。此外，也可从不同时段、不同运营状态的公交网络重要节点入手，研究重要节点的演化过程，为优化城市公交线网布局、提高公交出行效率、提升公交网络抗风险能力提供技术支撑。