基于多源数据的多式联运路径生成方法

李 弢，李绪茂

（1.武汉理工大学 交通与物流工程学院，湖北 武汉 430070；2.交通运输部规划研究院，北京 100028；3.综合交通规划数字化实验室，北京 100028；4.东南大学 交通学院，江苏 南京 210096）

0 引言

我国多式联运最早应用于外贸运输，多在长三角、珠三角和环渤海等经济较为发达的地区开展，但运量占比较低，2017 年我国多式联运量为13.68 亿t，占全社会货运量的2.9%[1]。随着社会经济的发展和产业结构的优化，大宗货物及中长距离货物的运输对多式联运的需求不断增加，加之国家层面对多式联运发展的政策支持，我国多式联运实现了快速发展，同时也出现了不同运输方式转换衔接成本高、信息互联共享难等问题，这吸引了越来越多不同领域的学者开展多式联运相关研究。

借助交通科学理论，构建科学的多式联运模型，模拟多式联运的运输组织，一直以来是学术界关注的焦点。多式联运涉及多种不同的运输方式，运输环境复杂多变，道路拥堵、极端天气等影响因素都会导致多式联运运输成本和运输时间的不确定性[2-3]。因此，在模型构建中考虑运输环境等影响因素能更精确和实际地反映运输过程，既有研究中，国内外学者也逐渐将不同的影响因素纳入多式联运模型中[4-7]。其中，运输环节出现问题是影响多式联运发展的重要方面，主要表现为节点堵塞[8-9]、转运设施中断[10]、在途运输道路拥堵等[11]。另外，出行时间的不确定性也是不容忽视的影响因素[12]。

多式联运作为货物运输研究的重要内容，其路径的生成和优化分析一直以来都是重中之重。在路径优化、组合优化等方面，通过考虑各种约束条件下的目标函数以及不同的标定参数建立多式联运路径优化模型，并利用最短路径算法、动态规划方法、启发式算法（蚁群算法、遗传算法等）等进行优化求解是相对成熟的研究思路[13-17]。在多式联运路径生成方面，还有些学者考虑到运输网络中多个节点存在服务时间窗的限制，建立了多个中间节点带软时间窗的多式联运运输路径优化模型[18]。除了考虑时间窗，近年来也有学者考虑碳排放和综合能耗等因素的影响，引入多目标算法等[19-24]进行研究。同时，智能优化算法被更多地运用在求解组合优化问题的领域，包括模拟退火、遗传、禁忌搜索以及蚁群等优化算法[25-26]。

综合来看，既有文献在多式联运路径生成研究方面形成了多样化的模型方法，对于解决特定情形下的特殊问题具有积极作用。多式联运作为全程一体化运输服务系统，具有涉及环节多、运营市场主体较多、业务关联度高等属性特征，是区域经济、产业不断发展的衍生产物。因此，多式联运的发展，尤其是其路径的生成研究需充分考虑区域产业的空间关联性和区域经济联系等现实因素。基于此，本文将以区域生产活动联系数据和区域经济关联数据为基础，整合基础设施网络数据以及货物运输活动数据，构建多源数据库，并考虑多种目标下的路径最优，提出不同维度的多式联运生成路径，以期为多式联运更好服务区域产业、经济发展提供参考。

1 样本数据与来源

研究数据包括基础设施网络数据、产业活动数据、区域生产活动联系数据以及货物运输活动数据4 种类型。其中，基础设施网络数据主要以全国地级市为节点，包含铁路、公路、水路和民航网络数据，主要来源于谷歌矢量地图。产业活动数据主要是全国各省（自治区、直辖市）的产业活动数据，来源于《中国统计年鉴》等提供的统计数据。区域生产活动联系数据由各种形式的投入产出表组成，借鉴区域投入产出表和企业抽样调研数据。货运活动数据主要是各省（自治区、直辖市）的货运活动数据，来源于全国公路水路运输量专项调查公报、高速公路门架检测等。

4 种类型的数据集相互支撑，共同构成了研究所用总数据库。其中，区域生产联系数据是整个货运需求生成与分布预测的数据基础，产业活动数据、货运运输数据以及交通运输基础设施网络数据为后续货运方式划分与流量分配及整个多式联运生成与优化提供支持。

2 多式联运路径生成的影响因素

多式联运涉及多个运输系统，不同的运输方式其属性并不相同，不同运输方式自身的特征和差异以及不同方式之间的有效衔接是影响多方式联运路径生成的重要因素。与此同时，多方式联运路径的生成，既受宏观层面的市场调控，又受微观层面承运货物种类、运距、运时等因素的影响。

1）多方式联运至少需要采用两种不同的运输方式实现运输过程。根据所采用的运输方式和组织管理的不同，交通运输方式可分为公路、铁路、水路、航空、管道5 种。因技术、成本因素等方面的差异，各种运输方式都拥有其独特的优缺点、适用范围（见表1）和内在要求，在运输领域发挥着各自不同的作用，其本身所具有的特征也成为影响多方式联运的重要因素。

2）基于多种运输方式组合优势的多方式联运系统的衔接以多方式联运系统整体效能最大化为目标，以系统内各要素间相互协调为导向，使系统处于和谐的发展状态。因此，它包括两层含义：一是指多方式联运系统内部的衔接。其基于各要素的协同效应，是系统内各子系统在总量分配上、空间布局上、技术水平上、组织管理上、管理政策上相互衔接。多方式联运系统是由货运枢纽站场、城市集配中心、仓库、线路（道路、铁路、航道等）等固定设施，运输车辆、船舶、装卸设备、承载设备、承载器等可移动设备，通信设备、计算机网络等物流信息管理手段，以及劳动力、资金等要素组成，这些要素的有机结合构成了整个联运系统。这一系统中包括了运输、配送、装卸、包装、流通加工和信息处理等作业环节，而它们之间是非线性相互作用。另一层含义主要体现在系统与外界需求总量上的衔接以及时空上的衔接。多方式联运系统中各部分的环节是相互联系的，需通过相关部门的衔接取得协同效果。其中包括将相关资源按照联运系统的要求进行配置集成、运作管理，将独立存在的部分衔接为整体时，需要部分的功能定位可以实现，部分之间在时空上的排列合理，各部分在规定的时间和空间范围内可以发挥功能等。

3）除此之外，多式联运路径生成还受到运输过程中的市场因素波动、人为因素干扰、运输费用变化、运输时间和运输距离长短、中转换装作业流程、货物的品类和运输安全性等多样化因素的共同作用和影响。

3 多式联运路径生成模型建立与求解

3.1 多式联运路径生成模型与求解算法的确定

多式联运路径的生成涉及多种不同的运输方式，每种运输方式又有不同的特征，同时不同运输方式之间的有效衔接也会对多式联运路径的生成产生影响。既有的多式联运路径生成模型与算法包括最短路径模型、改进k-shell模型、启发式算法等。不同的模型算法具有不同的优缺点，表2 对不同的多式联运路径生成模型求解算法进行了简要对比。

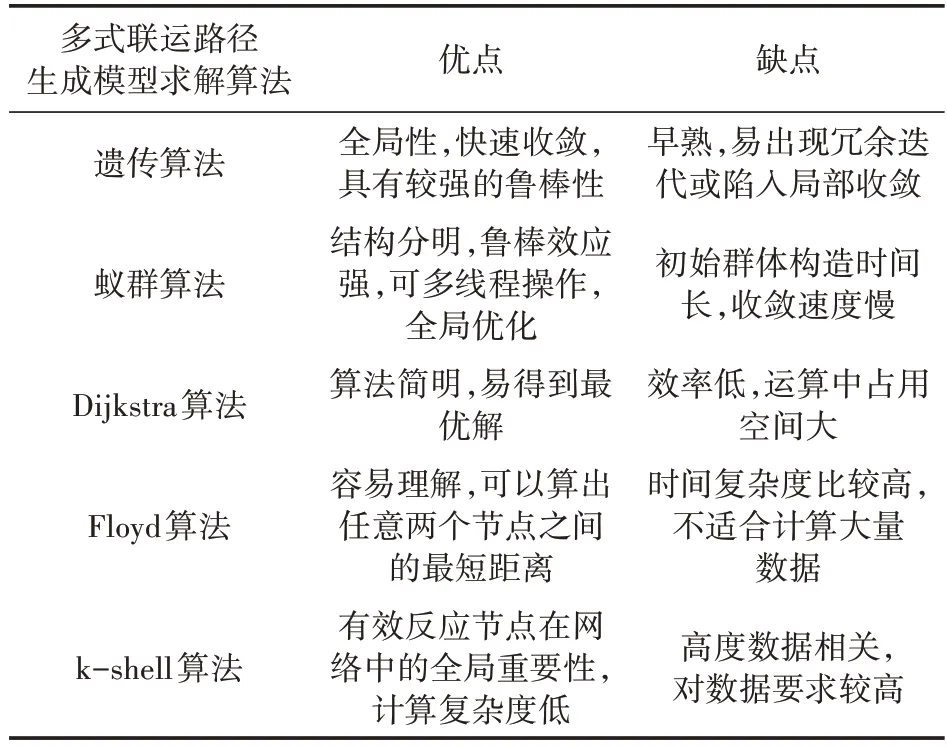
表2 多式联运路径生成模型求解算法对比

在对多式联运生成模型进行详细分析的基础上，本研究以阻抗模型为目标调节参数，确定以成本最优、时间最优、可靠性最优为目标建立多式联运路径生成模型。

3.2 多式联运阻抗模型

阻抗是多式联运模型中的重要目标调节参数。交通运输阻抗作为多式联运路径生成模型的目标选择参数，可用于标定时间、成本以及可靠性3 个目标。道路阻抗是路段交通状态的反馈，是衡量实际交通状态的重要指标。交通运输阻抗函数，简称路阻函数，是把交通阻抗定量化的数学表达式。不同阻抗类型的计算模型如表3所示。

表3 多式联运阻抗模型

3.3 多目标下的多式联运路径生成

多式联运路径规划问题的实质是路径与运输方式的组合优化问题，大部分研究在算法设计中将路径与运输方式的匹配视为“单向、单次选择”，即将路径与运输方式一并编码后统一计算得出适应度值，如此编码其实是路径与运输方式的随机匹配，没能体现两者组合寻优并且随着目标追求而多元化的计算实质。如何设计算法能使路径和运输方式都得到有效的搜索，并能满足成本、时间以及可靠性等不同目标的实现是关键。

3.3.1 成本最优路径

最短路径问题的一般表述为：给定一个赋权连通图，记作G=(N,L,C)，其中N={n1,n2,…,nn}为节点集；L={lij|lij=(ni,nj),i,j=1,2,…,n}为边集，对于边lij，相应的权重设为c(lij)=cij。给定有向图中的两个节点ns和nt，设pst为从起始节点ns到终止节点nt的一条路径，Pst={pst}为从ns到nt的所有路径构成的集合。定义路径pst的权为该路径中所有路段的权重之和，记为c(pst)。最短路径问题即为在Pst中搜索一条权重最小的路径p*，即则p*即为从ns到nt的最短路径。

利用Dijkstra 算法求解上述最短路问题。该算法基于最短路的最优性原理：如果从n1到nj的最短路径总沿着该路径从n1先到某点ni，然后再沿边lij=(ni,nj) ∈L到达nj，则n1到ni的这条路必定也是n1到nj的最短路径。具体求解步骤如下。

1）相关参数

O：起始节点；D：终止节点；N：网络节点集合；L：节点间路段的集合；i,j：节点记号；（i,j）：相邻节点i,j间的路段；cij：路段（i,j）的权重或属性（本研究采用阻抗参数来标定）。

2）决策变量

求解最短路径的过程本质上是路径的选择过程。为此，可采用如下二进制变量来表示路网上各路段的选择：

具体而言，当xij=1 时，对应的路段（i,j）将被选择为通行路段；否则，该路段将不会出现在所选路径上。

3）目标函数

莫言用优美的笔调营造了一个生机弥漫的红高粱世界。书中无处不在的茁壮、浓密、顽强的红高粱隐喻着生命的顽强，无边无际的高粱地是高密人爱恨情仇、精忠报国的场所。生活在汪洋血海的高粱地里的高密人，虽然面临贫穷、仇恨和死亡等痛苦和磨难，但同时逆境也激发了他们昂扬的斗志和张扬的个性。个体生命的张扬、毁灭、肢解都与红高粱地相融合。

在最短路问题中，通常将总权重作为所搜索路径的评价指标。相应地，最优权重所对应的路径即为需要搜索的最优路径。由决策变量可知，当路段（i,j）被选中时，其对应的权重为cijxij，则路径的总权重F(X)（即目标函数）可表示为：

式（2）中：cij为多式联运路段的阻抗参数。标定成本的阻抗参数cij计算公式为cij=pijLij，其中Lij表示路段长度；pij表示货物单位公里、单位吨位的平均运价。

4）约束条件

最短路径问题的求解中，通常要求所选择的路段需构成1 条从起始节点到终止节点的完整路径。为此，引入如下流平衡约束：

3.3.2 时间最优路径

多式联运作为广泛采用的快捷运输组织形式，其路径优化不仅要考虑成本最小化问题，整个运输过程的时效性也很重要。时间最优路径模型与成本最优路径模型不同的是路段权重cij的选择。在时间最优最短路径模型中，目标函数中的路段权重cij表示多式联运路段的阻抗参数，用于标定时间，其计算公式如下：

式（4）中：λ为货物在途价值系数，可以标定不同货物类别；qij为路段货运量；Qij为路段实际通行能力；t0为畅通无阻情况下的道路通行时间；α,β为模型的阻抗参数。

路径可靠性是指多式联运在面对扰动的情况下仍能保持令人满意的运输状态，即运输费用的增量小于网络失效的规模。本研究结合最小广义运输费用目标和BPR 函数构建多式联运阻抗模型，并提出了一种新的可靠路径搜索算法——改进k-shell 算法，用于求解多式联运路径生成问题，克服了传统的路径搜索Dijkstra 算法在网络中断时的不可行性，模型计算公式如下：

式（5）中：Z为路径序列的广义运输费用；为两节点间的直达路段阻抗；为不同运输方式节点的中转阻抗；w,k为不同的运输方式，取值分别为高速公路运输=1，国道运输=2，铁路运输=3，内河航道运输=4；W为运输方式的集合；K为运输方式改变后的集合；γij为0-1 变量，若货物在路段上通过则为1，否则为0；δij为0-1 变量，若货物在路段上需要改变运输方式则为1，否则为0。

式（6）约束了路段上的流量，其中：q为路段流量。式（7）约束了路段流量不超过路段容量，其中：Q为路段容量。式（8）表示路段阻抗，其中：为路段Eij采用运输方式w的广义运输费用；pij为货物的平均运价；Lij为路段长度；λ为货物在途价值系数；t0为通过路段的时间；α,β为回归参数。式（9）表示节点中转阻抗，其中：为运输方式w,k节点换装虚弧段Fij的广义运输费用；T(wk)为中转时间，下标数字1,2,3,4分别代表卸货时间、托运时间、装货时间、等待时间；dwk为运输方式w,k中转费用。式（10）表示节点阻抗的单位时间价值，其中：ξ为节点阻抗的单位时间价值；Ω为货物年均衰减率；P为货物的单位价值。

在可靠路径序列的搜索过程中，节点的运输重要性特征度量被用来衡量节点在路径上的重要程度。算法引入复杂网络理论中对于超网络中节点运输优势度的识别和筛选方法。

4 实证分析

4.1 货物参数分析

不同货物品类的运输特性不同，其在综合运输网络中的运输方式和运输路径的选择受到不同因素的影响。同时，综合运输网络中各种运输方式的技术经济特征不同，不同运输方式的线路阻抗函数和节点阻抗函数形式各异。

零担货物包括纺织品、造纸印刷、文教体育用品等。其一般价值较低，经济属性和物理属性不太适合采用集装箱运输。时效性强货物一般有新鲜蔬菜水果等食品、鲜活动植物、时装、展品和报刊等，其对运输时间和运输准时性要求较高。因此，时效性强的货物运输一般选择运送速度快、运输准时性强的运输方式。

运输费用通常是货主选择多式联运服务时的主要参考因素，而随着货运需求的差异化与运输产品的多样化程度增加，运输时间对多式联运服务选择结果的影响也逐渐凸显。运输费用对多式联运服务的影响可以通过参数货物平均运价P来表征，该参数取值可通过调查获得。运输时间对多式联运服务的影响则可通过货物在途价值系数λ来表征，其计算公式如下：

式（11）中：S为社会折现率。

表4 所示为通过调查获得的零担和时效性强两类货物的参数取值。

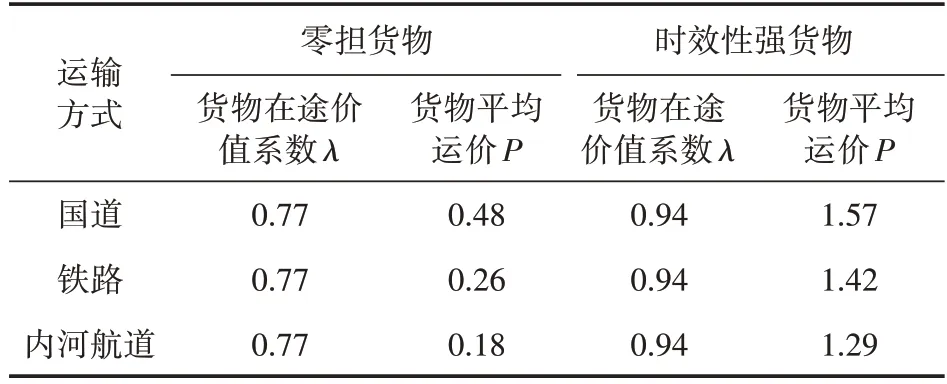
表4 货物参数表

4.2 网络分析

研究选取长三角城市群区域共涉及26个地级市的空间范围作为案例分析区域。为能清晰地表示拓扑网络数据，将长三角26个地级市按照高速公路、国道、铁路和内河航道4 种运输方式分为94个节点，共连接成1 158个路段（见表5）。

表5 实验网络基本信息表

在长三角多式联运拓扑网络的基础上，首先构建长三角多式联运无向无权超网络。然后对无向无权超网络进行赋权，构建长三角多方式运输网。图1所示为长三角多式联运超网络模型，将4种运输方式直达路段分为4 层网络，每层网络以长三角地级市为节点。其中，第1 层为高速公路直达网络；第2 层为国道直达网络；第3 层为铁路直达网络；第4层为内河航道直达网络。4种运输方式直达网络之间的连接路段为任意两种运输方式中转路段。中转路段由同一城市不同运输站点的货物换装过程和不同城市同一种运输方式的直达过程组成。

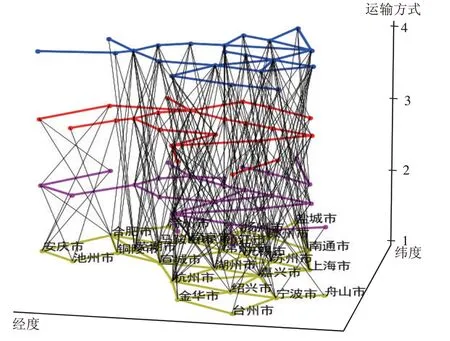
图1 长三角多式联运超网络模型

4.3 案例结果分析

在长三角多式联运超网络中，选取起始节点舟山市和终点滁州市分别运送1 t 零担货物和1 t时效性强货物。长三角地区的阻抗参数取值如表6 所示。选取各类运输方式主要枢纽节点，对其中转时间和中转费用进行统计，得到各类枢纽节点中转阻抗参数的取值结果，如表7所示。

表6 路段阻抗参数取值

表7 中转阻抗参数取值

1）成本最优路径

使用基于成本阻抗的最短路径模型进行实验，得到零担货物的成本最优路径为：舟山市经国道至绍兴市，绍兴市经内河至南京市，南京市经铁路至滁州市，路径序列的广义运输费用为301.69 元，运输时间为15.74 h。时效性强货物的成本最优路径为：舟山市经高速公路至苏州市，苏州经铁路至滁州市，路径序列的广义运输费用为343.56元，运输时间为11.93 h。

2）时间最优路径

使用基于时间阻抗的最短路径模型进行实验，得到零担货物的时间最优路径为：舟山市经高速公路至滁州市，路径序列的广义运输费用为485.32 元，运输时间为8.63 h。时效性强货物的时间最优路径为：舟山市经国道至杭州市，杭州市经高速公路至滁州市，路径序列的广义运输费用为516.43元，运输时间为6.48 h。

3）可靠性最优路径

针对零担货物，基于改进k-shell算法得到的可靠性最优路径为：舟山市经国道至湖州市，湖州市经高速公路至滁州市，路径序列的广义运输费用为397.51 元，运输时间为12.78 h。时效性强货物的可靠性最优路径为：舟山市经高速公路至无锡市，无锡市经铁路至滁州市，路径序列的广义运输费用为412.33元，运输时间为10.92 h。

上文对成本、时间和可靠性3 个目标进行了路径分析，3 个目标分别对应了不同的偏好。可以看出：以成本为偏好的路径结果费用最低，但耗时最长；以时间为偏好的路径结果耗时最少，但费用最高；以可靠性为偏好的路径结果耗时与费用居中，但抗风险和抗运输网络扰动的能力最强。

5 结束语

随着社会经济的发展，铁路、公路、水路和航空的运输环境都得到明显改善，多式联运将成为运输领域中的一个重要突破点。多式联运的运输过程涉及多个运输方式，需要进行方式选择并决策不同运输方式的衔接与配合，这就导致多式联运与普通的运输过程存在较大不同。本文首先分析了多式联运路径生成的影响因素，包括不同运输方式自身特征的影响、不同运输方式之间有效衔接的影响以及其他与运输过程相关因素的影响3 个方面；然后以成本最优、时间最优、可靠性最优为目标建立了多式联运路径生成模型，并通过对比分析，确定建立最短路径模型和改进kshell 算法进行多式联运的路径生成；最后以长三角地区为案例进行了多式联运路径生成实例分析。结果表明，多式联运的可靠性可通过运输环节中的运作时间、运输费用等方面的指标来评估，其既能有效反映出多式联运路网中不同运输线路的运输经济效益，又能表明运输过程中的可靠程度，可满足多式联运参与者的运输需求，促进多式联运的可持续发展。在未来研究中，将对多式联运物理设施网络进行评估，对区域乃至全国多式联运物理网中的节点和线路进行运输影响力评价，以进一步验证本研究所提出的模型在评价多式联运网络中线路和节点重要度及影响方面的适用性。