形状记忆合金变截面梁的相变力学行为分析
2023-09-27杨静宁韦子丰卢镜宇
杨静宁, 韦子丰, 卢镜宇, 王 鹏
(兰州理工大学 理学院, 兰州 730050)
形状记忆合金(SMA)是由两种或两种以上的金属元素复合而成的新型智能材料, 具有独特的超弹性和形状记忆效应, 且耐腐蚀、 抗疲劳和阻尼性较好[1]. 形状记忆合金在生物医疗、 航空航天工业和建筑结构等领域应用广泛[2-3].
目前, 研究人员对SMA材料的弯曲变形特性进行了研究. Flor等[4]在NiTi记忆合金丝弯曲实验的基础上, 分析了NiTi形状记忆合金丝在整个转变温度范围内的弯曲行为; Eshghinejad等[5]研究了横截面上应变呈线性分布的SMA悬臂梁在集中载荷作用下的变形特性; Auricchio等[6]基于SMA超弹性行为的一维模型推导出马氏体体积分数变化的演化方程; Brinson[7]研究了相变过程中的马氏体体积分数, 其中一部分马氏体相变由应力所致, 另一部分由温度所致; Shaw[8]通过具有超弹性和形状记忆效应的一维本构模型, 证明马氏体相变的不稳定性是由应变梯度效应所致; Raniecki等[9-10]描述了SMA超弹性的本构模型, 并研究了加载和卸载时超弹性对梁的弯曲行为影响, 通过研究拉压不对称性和相变屈服面, 得到马氏体体积分数在梁截面上的分布规律; Qidwai等[11]基于不同相变方程得到不同的本构模型; 周博等[12]分析和描述了SMA螺旋弹簧簧丝横截面的应变和应力分布规律, 推导出SMA螺旋弹簧相变临界参数的计算公式; 商泽进等[13]通过实验数据得到了SMA材料基于梁的大变形理论下应力应变关系; Rejzner等[14]研究了拉压不对称性对梁的相变行为影响; Chen等[15]通过分子动力学(MD)模拟研究了单晶和纳米晶NiTi形状记忆合金(SMAs)的拉伸-压缩不对称性; 崔世堂等[16]研究了在拉压不对称系数影响下形状记忆合金纯弯曲梁的力学性能; 杨静宁等[17]研究了拉压不对称系数对热-机载荷作用下形状记忆合金纯弯曲梁的影响; 考虑到拉压不对称性, Bouvet等[18]分别用两种不同的相变屈服面描述马氏体正相变和逆相变, 利用应力的第二和第三不变量定义相变屈服面, 得到了三维本构模型; 薛立军等[19]研究了一种由形状记忆合金和功能梯度材料按不同比例结合形成的新型复合材料; 韩悌信等[20]对NiTi形状记忆合金设计了动态情况下的三点弯曲实验, 研究了NiTi形状记忆合金的弯曲变形, 得到了TiNi合金的静态和动态情况下应力-应变曲线异于普通金属的结论.
目前, 对形状记忆合金梁的力学性能研究较多, 但对SMA变截面梁的研究较少. 在实际工程中, 为减轻结构质量或满足生产需要, 一些杆件经常采用变截面. 本文用分阶段分步骤方法分析相变过程, 研究SMA变截面梁在相变过程中机械载荷、 变截面系数和拉压不对称系数对中性轴位移、 曲率和相边界的影响.
1 SMA梁的非线性变形
1.1 几何模型
SMA变截面梁的几何模型如图1所示. 任意截面高度H(x)=λx+h0, 其中λ为变截面系数.
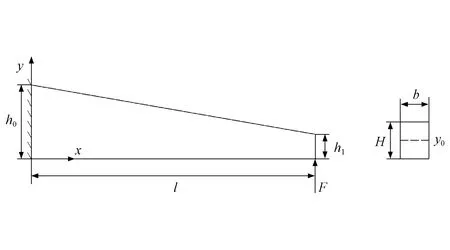
图1 SMA变截面梁的几何模型Fig.1 Geometric model of SMA variable cross section beam
1.2 本构模型
形状记忆合金材料的简化本构模型如图2所示[13], 其中σts和σtf分别为受拉侧相变开始和结束时的临界应力,σcs和σcf分别为受压侧相变开始和结束时的临界应力,εts和εtf分别为受拉侧相变开始和结束时的临界应变,εcs和εcf分别为受压侧相变开始和结束时的临界应变, Δεt为相变平台段.

图2 形状记忆合金的简化本构模型Fig.2 Simplified constitutive model for shape memory alloys
根据连续介质力学, 截面变形始终满足平面假设, 梁截面上的应变沿截面高度呈线性分布, 梁的轴向应变为

(1)
其中yi表示中性轴位置,ρ表示曲率半径.
1.3 拉压不对称系数
考虑到SMA变截面梁在弯曲变形过程中的非对称性, 特引入拉压不对称系数[21]

(2)
由计算可得

(3)
1.4 本构关系
随着弯矩的增大, 形状记忆合金变截面梁将经历一个由弹性变形到相变阶段的变形过程. 其中εt表示受拉侧的表层应变,εc表示受压侧的表层应变. 由平面假设可知, 在受载过程中相变首先发生在表层, 其相变过程分为Ⅰ~Ⅳ阶段.
1.4.1 初始阶段(εt<εts)
在初始阶段, 梁的整个截面均未发生相变, 材料全部为奥氏体相, 中性轴未偏移, 截面上的应力为
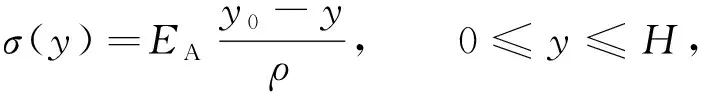
(4)
其中EA为奥氏体弹性模量,y0表示中性轴初始位置,y表示截面上点的位置.
1.4.2 相变阶段(εt≥εts)
随着应变逐渐增大并达到一定值时, 中性轴产生偏移, 梁的截面发生相变.任意截面及其微段的变形如图3所示, 其中A表示奥氏体相, M表示马氏体相, AM表示混合相. 当|εc|≤εcs,εts≤εt≤εtf时, 受拉侧出现混合相, 受压侧尚未发生相变, 奥氏体相与混合相形成相边界BTA, 进入Ⅰ阶相变, 如图3(A)所示, 截面上应力为
(5)
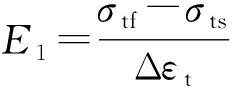
当εcs≤|εc|≤εcf,εts≤εt≤εtf时, 受压侧表层开始发生相变并出现混合相, 受压侧混合相与奥氏体相形成相边界BCA, 进入Ⅱ阶相变, 如图3(B)所示, 截面上应力为
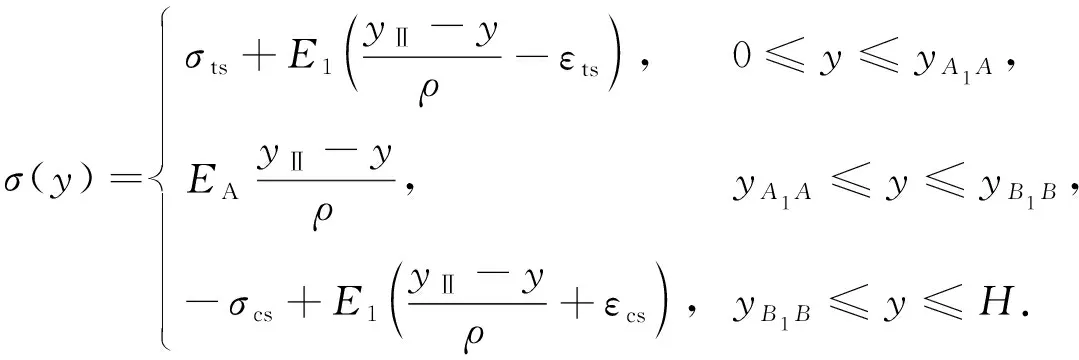
(6)
当εcs≤|εc|≤εcf,εtf≤εt时, 受拉侧表层应变εt超过受拉侧相变结束临界应变εtf, 受拉侧表层出现马氏体相, 而受压侧表层仍处于混合相, 受拉侧混合相与马氏体相形成相边界BTM, 如图3(C)所示, 进入Ⅲ阶相变, 截面上应力为
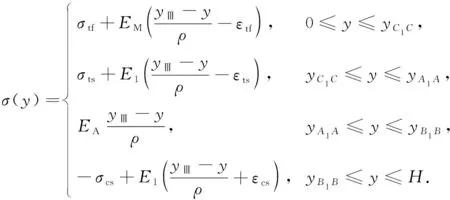
(7)
当εcf≤|εc|,εtf≤εt时, 受压侧表层应变εc超过受压侧相变结束临界应变εcf, 受压侧表层出现马氏体相, 受压侧混合相和马氏体相形成相边界BCM, 进入Ⅳ阶相变, 如图3(D)所示, 截面上应力为

(8)
其中yi(i=Ⅰ,Ⅱ,Ⅲ,Ⅳ)表示不同阶段截面上中性轴位置, Δh=yi-y0表示中性轴位移, 相边界A1A,B1B,C1C和D1D的坐标可分别为yA1A=yi-εtsρ,yB1B=yi+εcsρ,yC1C=yi-εtfρ,yD1D=yi+εcfρ.
1.5 内力方程
设任意截面上的弯矩为M(x).在初始阶段, 梁的内力方程为
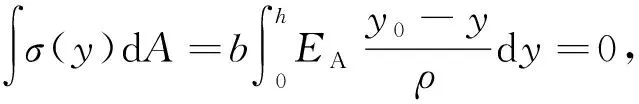
(9)
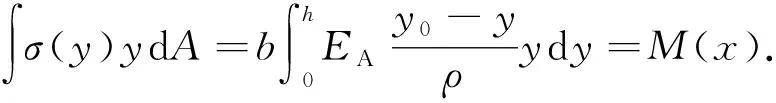
(10)
在Ⅰ阶相变阶段, 梁的内力方程为

(11)
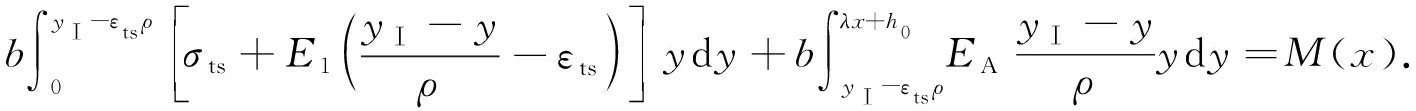
(12)
在Ⅱ阶相变阶段, 梁的内力方程为
在Ⅲ阶相变阶段, 梁的内力方程为
在Ⅳ阶相变阶段, 梁的内力方程为
2 结果与讨论
设SMA变截面梁长l=200 nm, 截面宽b=8 mm, 梁高h0=6 mm,h1=λl+h0, 受集中载荷F作用, 几何模型如图1所示.TiNi合金材料成分为Ti50.9Ni, 材料相关参数[17]分别为
EA=62 GPa,EM=62 GPa,E1=4.5 GPa,σts=465 MPa,σtf=645 MPa, Δεt=0.04.
2.1 有限元对比
为验证本文结果的可靠性和理论的正确性, 对图1所示的几何模型用有限元方法和本文的理论分析方法[17]分别对x=50,100,150 mm 3个截面处应力进行计算. 利用有限元软件ABAQUS建立计算模型, 选用C3D8R单元, 网格划分的精度为1 mm. 当F=250 N时, 应力随梁截面高度分布如图4所示, 其中图4(A)为初始阶段, 图4(B)和图4(C)均为相变阶段. 由图4可见, 截面越靠近端部, 数据越理想, 理论结果与有限元结果总体上吻合良好.

图4 应力随截面高度的分布 Fig.4 Distribution of stress with cross section height
2.2 横截面应力分布
图5为x=100 mm处横截面的应力分布. 由图5(A)可见: 当拉压不对称系数α=0时, 拉压两侧应力呈对称分布; 拉压不对称系数越大, 受压侧同一高度混合相处的应力越大, 奥氏体相处的应力越小; 拉压不对称系数对受压侧影响大于受拉侧. 由图5(B)可见, 变截面系数对受拉侧和受压侧的影响均较大, 且变截面系数越大, 截面混合相所占比例越大, 同一高度处应力也越大.

图5 截面上的应力分布Fig.5 Stress distribution on cross sections
2.3 中性轴位移
中性轴位移和截面位置的关系如图6所示. 进入相变阶段后, 载荷和变截面系数对中性轴位移影响较大.由图6(A)可见, 随着载荷的增大, 中性轴位移最大值的截面位置越靠近梁中间截面, 在梁弯矩较小截面处, 中性轴向受压侧偏移, 在梁弯矩较大截面处, 中性轴向受拉侧偏移. 由图6(B)可见, 拉压不对称系数导致中性轴产生位移, 拉压不对称系数变大, 中性轴的偏移量增大, 与文献[16]结果相符. 由图6(C)可见, 改变变截面系数对梁两端的影响较小, 在相变阶段, 中性轴位移的最大值随变截面系数的增大而减小, 变截面系数越大, 中性轴位移最大值的截面也越靠近中间截面.
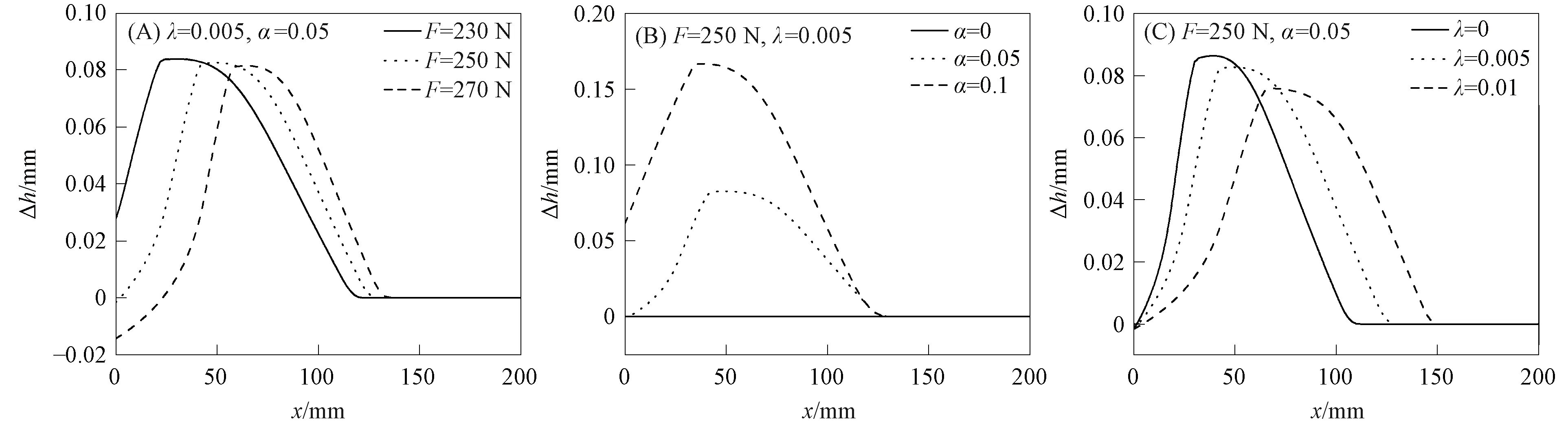
图6 中性轴位移和截面位置的关系 Fig.6 Relationship between neutral axis displacement and cross section position
2.4 曲 率
曲率和截面位置的关系如图7所示. 进入相变阶段后, 载荷和变截面系数对曲率影响较大. 由图7(A)可见, 曲率的最大值随集中载荷的增大而增大, 在相变阶段, 载荷对曲率的影响比初始阶段更明显. 由图7(B)可见, 在初始阶段, 改变拉压不对称系数对曲率影响较小, 但在相变阶段影响较大. 由图7(C)可见, 改变变截面系数对梁两端曲率的影响较小, 而对梁中间部分截面影响较大, 在同一截面, 变截面系数越大, 曲率越大.
2.5 相边界
相边界和截面位置的关系如图8所示. 在相变阶段, 载荷和变截面系数对相边界影响较大, 拉压不对称系数对受拉侧相边界的影响较小.
由图8(A)可见: 随着集中载荷的增大, 马氏体部分由梁根部逐渐向梁中部扩散; 混合相和奥氏体的相边界与马氏体和混合相的相边界整体向梁受载小的部分移动. 由图8(B)可见, 增大拉压不对称系数对受拉侧影响较小, 但受压侧奥氏体和混合相的相边界逐渐靠近梁受载大的部分. 由图8(C)可见, 随着变截面系数的增大, 奥氏体和混合相相边界与混合相和马氏体相边界整体向梁端部移动, 且影响较大.
综上, 本文在考虑拉压不对称性的基础上得到了梁截面上应力的解析表达式, 通过有限元计算验证了本文理论计算方法的可靠性, 并讨论了变截面系数对中性轴位移、 曲率和相边界的影响, 得到如下结论:
1) 在相变阶段, 载荷越大, 中性轴位移最大值的截面位置越靠近梁中间截面; 中性轴位移随拉压不对称系数的增大而增大; 中性轴位移的最大值随变截面系数的增大而减小, 变截面系数越大, 中性轴位移最大值的截面越靠近中间截面.
2) 在梁载荷较小的部分, 变截面系数和拉压不对称系数对中性轴、 曲率和相边界的影响较小; 在梁载荷较大的部分, 梁进入相变阶段, 曲率在弯矩最大值处达到最大值, 且曲率的变化量随载荷的增大而增大.
3) 载荷和变截面系数越大, 相边界越远离截面边缘; 拉压不对称系数越大, 受压侧越不易发生相变, 但对受拉侧影响较小.
