离散Bayes网诱导的概念类VC维数的下界

罗亭亭, 李本崇

(西安电子科技大学 数学与统计学院, 西安 710126)

Bayes网络[1], 也称为概率网络、 信念网络或者因果网络, 是一种用有向无环图表示随机变量间条件独立关系的统计模型, 最初主要用于处理人工智能中的不确定性信息, 目前广泛应用于不确定性推理和机器学习等领域[2-6]. Bayes网络通过若干条件分布的乘积表示复杂的联合概率分布, 因此有助于处理高维统计问题.

VC(Vapnik-Chervonenkis)维数和欧氏嵌入维数是二值函数类复杂性的两种度量[7], 离散Bayes网络诱导的概念类的VC维数和欧氏嵌入维数的大小备受关注. Kearns等[8]研究了一般概念学习的形式化模型, 着重研究了概念类的可学习性和一致收敛性, 并给出了许多有效算法; García-Puente等[9]给出了离散Bayes网的代数几何刻画; Nakamura等[10]给出了二值随机变量Bayes网诱导的概念类欧氏嵌入维数的上下界, 并确定了一些特殊Bayes网诱导的概念类欧氏嵌入维数的精确值; Yang等[11-12]针对Boolean域上的二分类任务, 证明了完全Bayes网和几乎完全Bayes网诱导的概念类的VC维数和欧氏嵌入维数相等; Yang等[13]针对随机变量取值均为k个的二分类问题, 证明了任意不含有V-结构的Bayes网诱导的概念类VC维数和欧氏嵌入维数的一致性, 并给出了计算该维数的显示公式; Yang等[14]针对变量在Boolean域取值的Bayes网, 证明了随机变量个数不超过5时, Bayes网络诱导的概念类的VC维数与欧氏嵌入维数相等; Varando等[15]用Lagrange多项式乘积的线性组合评估Bayes网的表达能力, 得到了与文献[13]类似的结果; Li等[16]扩展了Yang等[13]以及Varando等[15]的结果, 证明了任意不含V-结构的Bayes网诱导的概念类VC维数和欧氏嵌入维数的一致性, 并给出了一般Bayes网诱导的概念类欧氏嵌入维数的上界(VC维数的上界). 近年来, 研究者们已利用Bayes网络模型解决了许多实际问题[17-19], 但对Bayes网诱导的概念类的复杂性理论研究目前尚未见文献报道. 当一个网络中的每个随机变量取任意有限个值时, 该Bayes网络诱导的概念类VC维数的下界尚无一般性结果. 因此, 基于Yang等[13]的工作, 本文考虑一般的离散Bayes网络诱导的概念类VC维数的下界, 为进一步研究Bayes网诱导的概念类的复杂性做铺垫, 并为分类任务提供理论支撑.

1 预备知识

定义1[1]如果一个有向图从任意顶点出发, 沿任意若干条有向边都不能回到该点(不含有向环), 则称该图是一个有向无环图, 记作G=(V,E).每个顶点Xi∈V表示一个随机变量, 一个有向边(Xi,Xj)∈E表示Xi和Xj之间的条件依赖性, 其中V={X1,X2,…,Xn},i,j∈{1,2,…,n}且i≠j.

图G中若(Xi,Xj)∈E, 则Xi称为Xj的父节点,Xj称为Xi的子节点.本文用PA(Xi)表示节点Xi的父节点集合,mi=|PA(Xi)|表示父节点的个数.一个有向图是完全的当且仅当给定节点的拓扑序时, 对每个节点Xi都有PA(Xi)={X1,X2,…,Xi-1}.令X,Z,Y是有向无环图G=(V,E)的3个节点, 如果G中包含有向边X→Z和Y→Z, 且X和Y在G中不相邻, 则称(X,Z,Y)是一个V-结构, 如图1所示.

图1 图G的一个V-结构Fig.1 A V-structure of graph G

每个有向无环图G都对应一个概率分布族P,P由X上有如下形式的概率分布组成:

(1)

其中p(Xi|PA(Xi))表示给定父变量PA(Xi)时Xi的条件概率.

定义2(Bayes网)[2]一个Bayes网由有向无环图G=(V,E)和分布族P构成, 记作N=(G,P).

例1如图2所示的一个有向无环图, 节点集V={X1,X2,X3,X4}, 有向边集合E={(X1,X2),(X1,X3),(X2,X4),(X3,X4)}.由式(1)可知, 该有向无环图对应的概率分布族中的每个分布P满足

图2 一个有向无环图Fig.2 A directed acyclic graph

P(X)=p(X1)p(X2|X1)p(X3|X1)p(X4|X2,X3).

考虑N是一个有n个节点X1,X2,…,Xn的Bayes网,Xi∈[ki], 其中ki∈,ki≥2,i=1,2,…,n.易知若PA(Xi)={Xi1,Xi2,…,Xir}, 观测向量为x=(x1,x2,…,xn), 则xpa(xi)≜(xi1,xi2,…,xir).将N对应的分布族记为DN,DN中X上的任一概率分布由如下形式表示:

(2)

记Bayes网络N可自由设定的参数个数为FA(N), 基于上述讨论可知参数个数应为所有变量可自由设定的参数数目之和, 即

(3)

根据式(3), 对完全的Bayes网络NF, 其可自由设定的参数个数为

(4)

例2以图2对应的Bayes网络为例,X=(X1,X2,X3,X4),Xi取ki个值,i=1,2,3,4.若x=(1,0,1,2), 则由PA(X4)={X2,X3}可得xpa(x4)=(0,1).若变量X1,X2,X3,X4对应的可自由设定参数个数分别为k1-1,k1(k2-1),k1(k3-1),k2k3(k4-1), 则由式(3)可得该Bayes网络的可自由设定参数个数为k1-1+k1(k2-1)+k1(k3-1)+k2k3(k4-1).

定义3[10]概念类C是定义在X上的一个函数族, 满足f:X→{-1,1}, 每个f∈C称为一个概念.

定义4[10]一个有限集合S={s1,s2,…,sm}⊆X称为被概念类C打散是指对任意m维向量b∈{-1,1}m, 存在f∈C使得f(si)=bi, 其中i=1,2,…,m.

定义5[10]概念类的VC维数定义为

VC dim(C)=sup{m|S⊆X,S被C打散, 且|S|=m}.

(5)

若由任意数目的样本点组成的集合都能被概念类C打散, 则该概念类的VC维数即为无穷大.

(6)

由定义5和定义6可得Bayes网诱导的概念类的VC维数, 将CN的VC维数记作VCdim(N).欧氏嵌入维数是用来评价Bayes网分类能力的另一个常用指标, 其定义如下:

定义7[10]给定X上的一个概念类C和一个具有标准内积的d维欧氏空间, 若存在d中的向量(uf)f∈C和(vx)x∈X, 使得∀f∈C,x∈X, 有则称概念类C可以嵌入到d维欧氏空间.使C可以被嵌入d中最小的d称为概念类C的欧氏嵌入维数, 记作Edim(C).

对于一个概念类C, 如果不存在有限维的欧氏空间可以被C嵌入, 则Edim(C)为无穷大.概念类CN的欧氏嵌入维数记作Edim(N).

例3考虑图2对应的Bayes网, 若Xi∈{0,1},i=1,2,3,4, 则VCdim(N)=Edim(N)=11[12].

命题1[10]对每个有限概念类C, 均有Edim(C)≥VCdim(C).

命题1表明,CN的欧氏嵌入维数是其VC维数的上界.完全Bayes网络诱导的概念类的VC维数和欧氏嵌入维数皆等于网络中可自由设定的参数个数[20].

命题2[13]设N′是有(n-1)个变量的Bayes网络,N中有向无环图去掉节点Xn及与之相连的有向边后对应的Bayes网为N′, 若S′⊆[k]n-1被N′打散且VCdim(N′)=|S′|, 则

VCdim(N)≥VCdim(N′)+(k-1)k|PA(Xn)|,

(7)

其中Xi∈[k],i=1,2,…,n.

命题2表明, 一个有n个k-值随机变量的Bayes网络诱导的概念类VC维数的下界是前(n-1)个变量组成的Bayes网络诱导的概念类VC维数与最后一个变量对应的可自由设定的参数个数之和.

定理1[13]设N是一个离散的非完全Bayes网络, 其有n个变量X1,X2,…,Xn, 且每个变量Xi∈[k],k∈,k≥2, 则

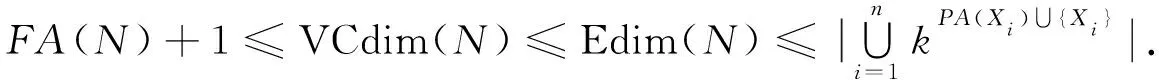
(8)

定理2[16]设N是一个有n个随机变量, 无V-结构的非完全Bayes网络, 且每个变量Xi∈[ki],ki∈,ki≥2, 则

VCdim(N)=Edim(N)=FA(N)+1.

(9)

定理1给出了当随机变量取值个数均为k时, 非完全Bayes网络诱导的概念类VC维数和欧氏嵌入维数的上下界.定理2表明, 不含有V-结构的非完全Bayes网诱导的概念类的VC维数和欧氏嵌入维数相等.

2 概念类VC维数的下界

Yang等[13]证明了当X=(X1,X2,…,Xn)在[k]n上取值时, 非完全Bayes网中得到的VC维数的下界为可自由设定的参数加1.本文推广该结果, 考虑网络中每个随机变量Xi∈[ki](ki∈,ki≥2)时该Bayes网诱导的概念类VC维数的下界.

首先给出一个引理, 其本质是在定义Bayes网诱导的函数类时, 若函数类中不包含(1,1,…,1), 则可改写符号函数的定义, 以避开样本点概率相等的情形.

引理1设N是有n个变量X1,X2,…,Xn的Bayes网络, 其中Xi∈[ki],ki∈,k≥2,i=1,2,…,n,N诱导的概念类为CN, 则对每个k1k2…kn维的向量b=(b1,b2,…,bk1k2…kn)∈CN-{(1,1,…,1)}都存在一对分布P,Q∈DN, 使得:

1) sign[log(P(xk)/Q(xk))]=bk;

证明: 当n=1时,N是一个完全Bayes网络, 此时的结果是文献[13]中引理3.4的一个特例, 因此当n=1时结论成立.

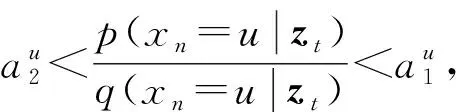
命题3[13]设a是一个非负实数,b是一个m维向量, 其中

b=(b1,b2,…,bm)∈({1,-1}m-{(1,1,…,1),(-1,-1,…,-1)}),

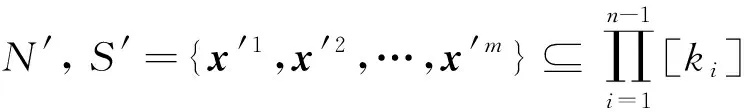
(10)

{x′m+1|PA(Xn),x′m+2|PA(Xn),…,x′m+d-t|PA(Xn)}={zt+1,zt+2,…,zd},

且zt+1,zt+2,…,zd均不相同, 其中zt+1,zt+2,…,zd都是r维的.取

S3={(x′i,1),(x′i,2),…,(x′i,kn-1)|i=m+1,…,m+d-t},

易知S1∩S2=Ø,S1∩S3=Ø,S2∩S3=Ø.现令S=S1∪S2∪S3, 则有

下面证明∀b=(b1,b2,…,bm,bm+1,…,bm+d(kn-1))∈{1,-1}m+d(kn-1), 存在一对分布P,Q∈DN, 使得

sign[log(P(si)/Q(si))]=bi,i=1,2,…,m+d(kn-1),

① (bi,0,bi,1,…,bi,kn-1)∈{(1,1,…,1),(-1,-1,…,-1)}, (bj1,0,…,bjl,0)∈{1,-1}l.

首先考虑si,0,si,1,…,si,kn-1, 可以指定参数p(xn=u|zi)=q(xn=u|zi), 选择分布P′,Q′只需满足P′(x′i)≥Q′(x′i)或P′(x′i)

② (bi,0,bi,1,…,bi,kn-1)∈{1,-1}kn-{(1,1,…,1),(-1,-1,…,-1)}, (bj1,0,…,bjl,0)∈{1,-1}l.

首先考虑si,0=(x′i,0)∈Ai, 由引理1知, 若bi,0=1, 则选择分布P′,Q′时需满足P′(x′i)>Q′(x′i); 若bi,0=-1 , 则选择分布P′,Q′时需满足P′(x′i)Q′(x′j); 若bj,0=-1, 则选择分布P′,Q′时需满足P′(x′j)

引理2是命题2的推广, 它表明当Bayes网络中每个随机变量取任意有限个值时, 该网络诱导的概念类的VC维数大于或等于前(n-1)个变量组成的Bayes网络诱导的概念类的VC 维数与最后一个变量的可自由设定参数个数之和.在引理2的基础上, 结合定理2, 有下列结论.

定理3设N是一个有n个节点X1,X2,…,Xn的非完全Bayes网络, 其中Xi∈[ki],ki∈,ki≥2, 则

(11)

证明: 当n=1时,N1是一个完全Bayes网络, 此时VCdim(N1)=FA(N1)=k1-1[13,16].考虑非完全Bayes网从n=2开始, 由定理2知, VCdim(N2)=k1+k2-1,FA(N2)=k1+k2-2, 结论成立.

假设该结论对任一有(n-1)个变量X1,X2,…,Xn-1的非完全Bayes网Nn-1成立, 且Xi∈[ki], 则

证毕.

定理3给出了所有离散非完全Bayes网诱导的概念类VC维数的下界, 对此说明如下.

(i) 当Bayes网络不含有V-结构时, 此类Bayes网诱导的概念类VC维数的下界正是VC维数[16].

(ii) 当Bayes网络含有V-结构时, 有些情况下这个下界恰为VC维数.例如, 图1所示的有向图对应的非完全Bayes网络, 令X,Y,Z∈{0,1}, 则该Bayes网络的可自由设定参数个数为1+2×2+1=6, 其诱导的概念类VC维数的下界为6+1=7, 这与Yang等[14]证明的该Bayes网诱导的概念类VC维数等于7一致.

(iii) 在Bayes网络含有V-结构时, 这个下界有时偏小. 例如, 图2对应的Bayes网络含有一个V-结构, 当X1,X2,X3,X4∈{0,1}时, 该Bayes网诱导的概念类VC维数的下界为1+2+2+4+1=10, 而Yang等[12]证明了该Bayes网诱导的概念类VC维数为11.

综上所述, 本文主要讨论了一般Bayes网诱导的概念类VC维数的下界问题. 对每个随机变量都可取任意有限值的任一非完全Bayes网络, 考虑其诱导的概念类的VC维数与网络中可自由设定的参数个数的关系, 证明了任意非完全离散Bayes网的可自由设定参数个数加1后, 是该Bayes网诱导的概念类VC维数的一个下界. 对于没有V-结构的非完全Bayes网络, 本文给出的这个下界恰好是VC维数[16]; 对于含有V-结构的非完全Bayes网络, 这个下界可能等于VC维数, 也可能小于VC维数. 本文的研究结果对任一非完全Bayes网络都适用, 解决了一般Bayes网诱导的概念类VC维数的下界问题, 为进一步研究Bayes网诱导的概念类的复杂性提供了参考.