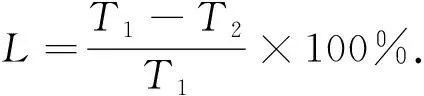基于min-max准则与区域划分的I-k-means-+聚类算法
2023-09-27曲福恒宋剑飞胡雅婷潘曰涛
曲福恒, 宋剑飞, 杨 勇,2, 胡雅婷, 潘曰涛
(1. 长春理工大学 计算机科学技术学院, 长春 130022;2. 长春师范大学 教育学院, 长春 130032; 3. 吉林农业大学 信息技术学院, 长春 130118)
聚类分析是一种将数据集按相似性进行分组的方法, 其目的是为使组内的数据更相似, 同时使组间的数据差异更大[1]. 聚类常用于数据挖掘、 模式识别、 决策支持、 机器学习和图像分割等领域[2].k-means是最流行的聚类算法之一, 具有实现简单、 执行效率高等优点, 但易陷入局部最优解[3], 导致聚类性能不佳.
针对上述问题, 目前已提出了多种改进方案. Likas等[4]提出了全局k-means算法, 首先使用数据集的质心作为第一个簇中心, 然后逐个增加簇中心并使用k-means算法找到收敛位置, 以提高算法的聚类精度; Nayak等[5]提出了一种基于粒子群优化的k-means聚类算法, 以获得最优的聚类中心; 为选取合适的聚类中心, Erisoglu等[6]提出了一种根据变异系数和相关系数计算k-means初始聚类中心的算法; Rahman等[7]提出了一种基于遗传算法的聚类技术, 通过改进初始种群的选择方法产生高质量的聚类中心; 邢长征等[8]提出了一种基于平均密度优化初始聚类中心的k-means算法, 有效提高了算法的聚类精度; Tzortzis等[9]提出了根据方差为簇分配权重的方法, 限制了大方差簇的出现, 并且提高了求解精度; Malinen等[10]在k-means算法分配阶段通过匈牙利算法解决各簇分配问题, 使簇之间达到平衡; Pham等[11]提出了一种增量式搜索策略减少算法对初始中心的依赖性; Bagirov[12]通过最小化提出的辅助聚类函数计算新增聚类中心的起点, 有效提升了全局k-means算法的精度.
上述算法虽然精度提升明显, 但与k-means算法相比时间复杂度较高. Ismkhan[13]以k-means为基础提出了一种新的迭代聚类(I-k-means-+)算法. I-k-means-+算法时间复杂度较低, 与k-means算法基本相当, 且在一定程度上提高了k-means算法的聚类精度. I-k-means-+算法利用数据点到有用中心的距离选择k个初始中心, 然后通过不断地划分、 删除簇优化k-means算法的目标函数值. 但因随机划分方式导致聚类结果不稳定, 聚类精度仍有较大提升空间. 针对I-k-means-+算法存在的问题, 本文提出一种基于min-max准则与区域划分的I-k-means-+聚类算法. 该算法在选择初始中心时, 计算数据到最近中心的距离, 优先选择距离较远的数据点作为新的聚类中心, 以避免初始中心过于密集的情况; 采用多区域划分的策略增加候选中心的多样性; 通过重新选择分裂簇, 并与原删除簇再次配对提高配对成功率.
1 I-k-means-+算法
假设给定一组具有N个样本的数据集X={x1,x2,…,xN},xi∈D(i=1,2,…,N), 聚类的目的是将数据集划分为k个互不相交的子集(簇){S1,S2,…,Sk}, 聚类中心集合为C={C1,C2,…,Ck}.
k-means算法使用误差平方和(SSE)作为衡量聚类效果的指标. 对于给定的解S=(S1,S2,…,Sk), SSE的计算公式为
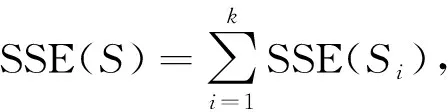
(1)
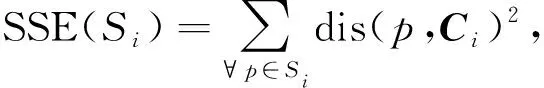
(2)
其中dis(p,Ci)为样本点p到所属聚类中心Ci的欧氏距离.I-k-means-+算法首先计算每个数据点的有用中心.
定义1如果不存在中心Cy满足如下条件:
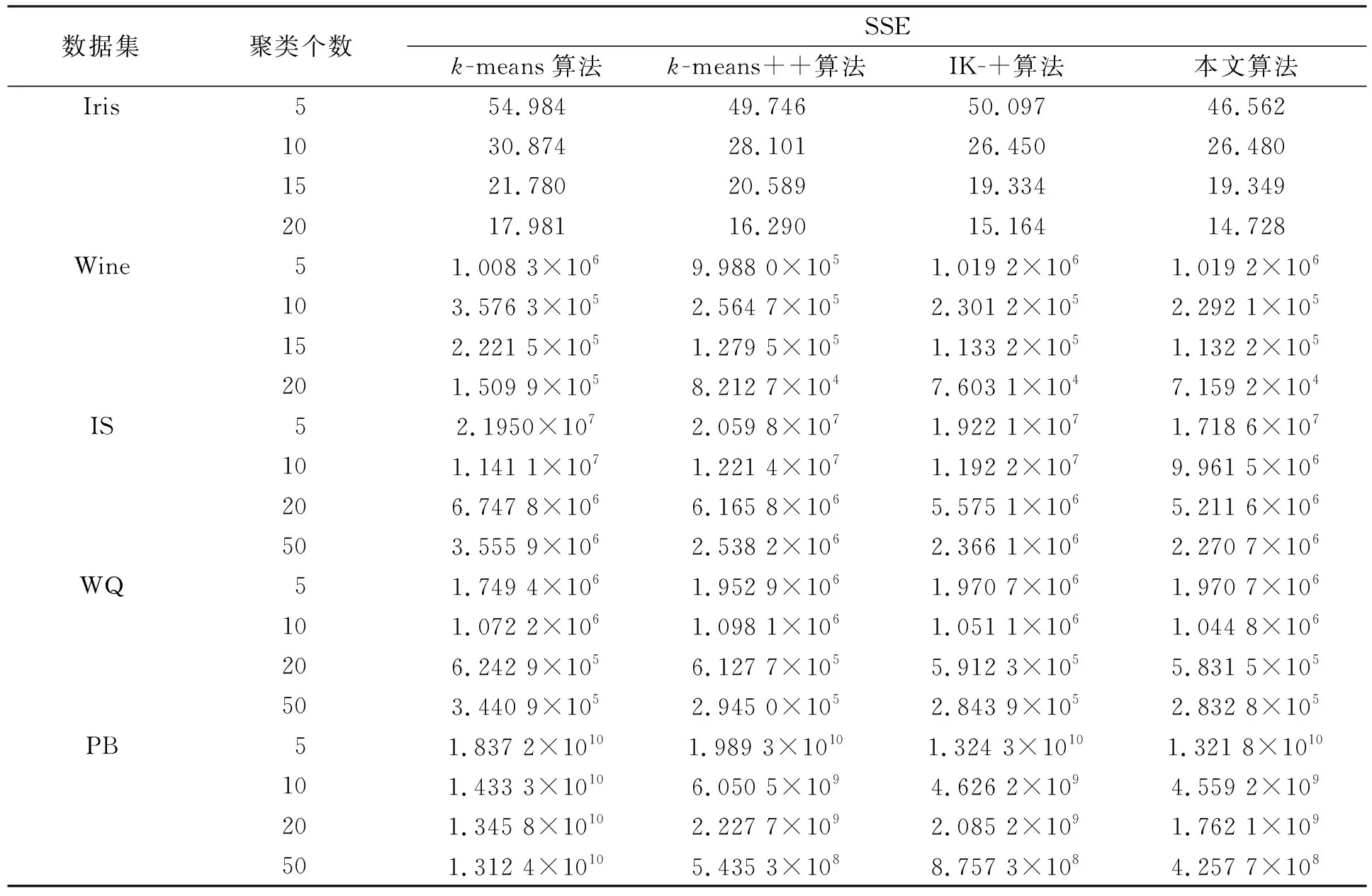
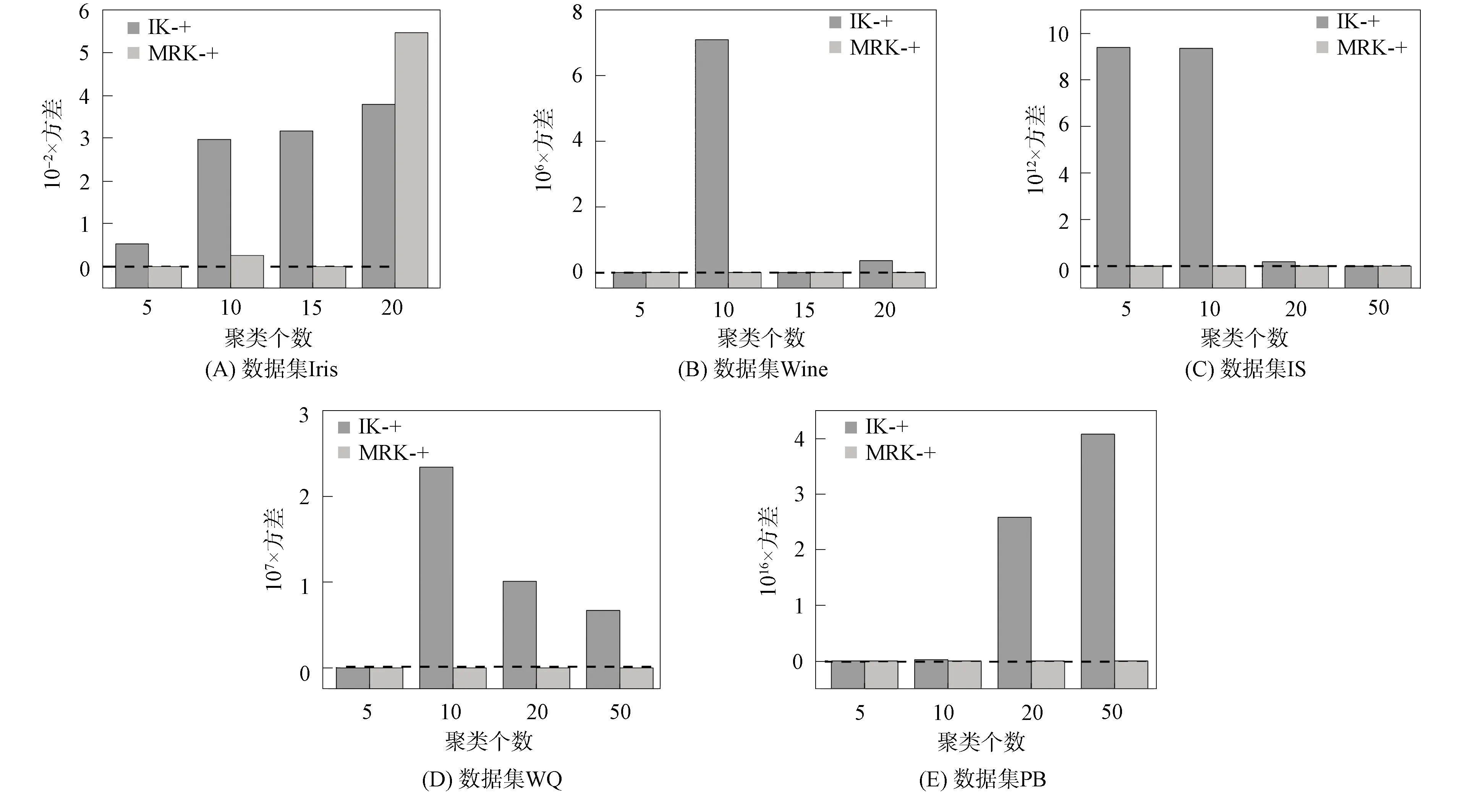
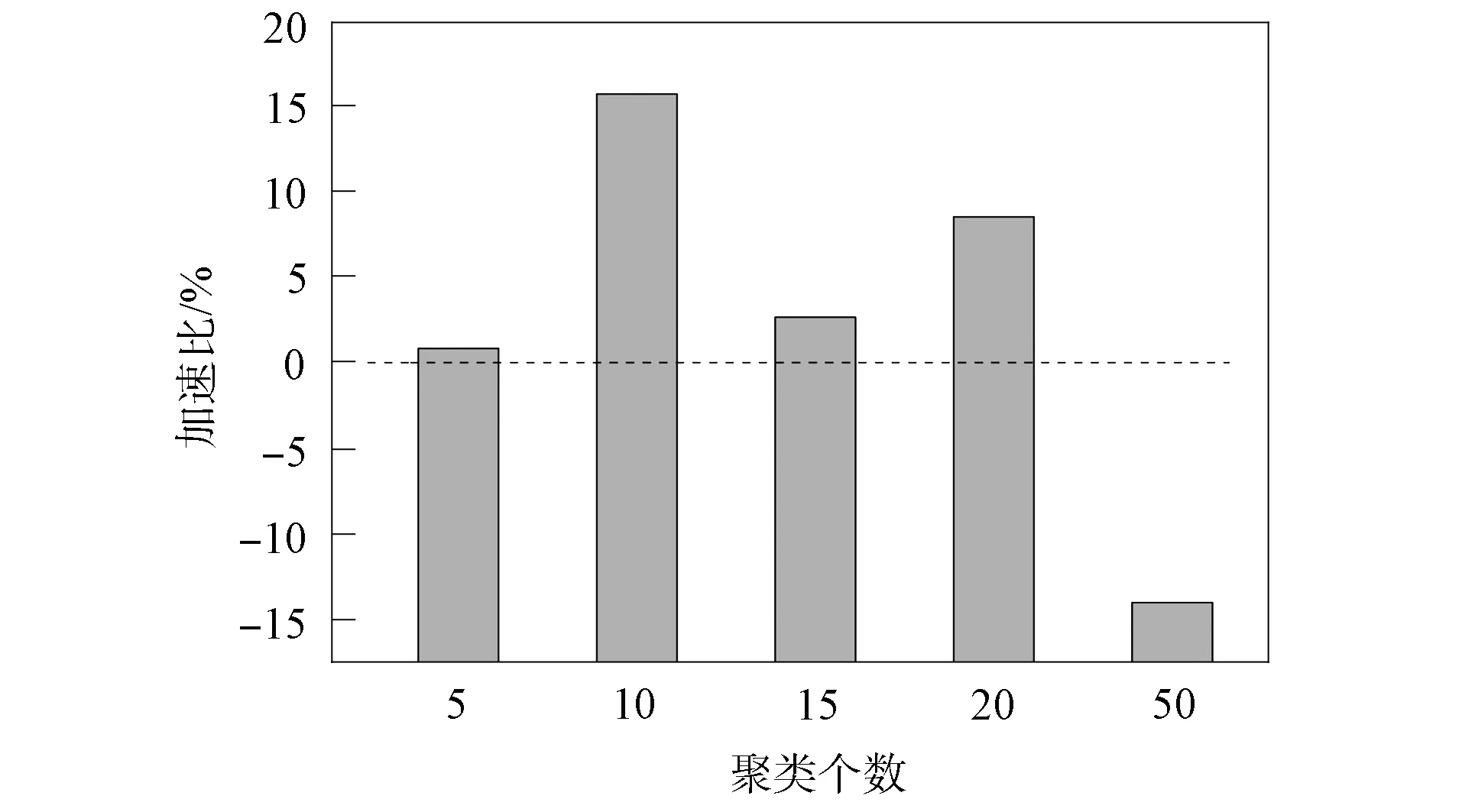
(dis(p,Cy) 则称中心Cx为数据点p的有用中心. 先通过 (3) 计算每个数据点p的权重, 即V1(p,C), 根据权重选择k个初始聚类中心, 并使用k-means算法收敛为解S, 其中Hp是数据点p的有用中心集合; 然后选择增益较大的簇Si与损失较小的簇Sj, 删除簇Sj并划分簇Si, 使用t-k-means[13]收敛为解S′; 最后保留S和S′中精度最高的解.增益(Gain)和损失(Cost)的计算公式分别为 (4) (5) 其中Zp是数据点p的次近中心。在实际应用中, 各中心之间的分布并非绝对均匀, 不同区域的聚类中心密集程度不同.由I-k-means-+算法过程可知, 该算法的初始中心选择方法仅考虑有用中心对数据点权重的影响, 当有用中心与所有中心的数量差距较大时, 有用中心很难反应出所有中心的分布情况.从而导致算法选择的多个初始中心在同一个簇中, 而有的簇没有聚类中心, 如图1所示.I-k-means-+算法的聚类精度易受初始中心影响, 图1的初始解较差更易使算法陷入局部最优解, 降低算法的求解精度. 图1 I-k-means-+算法在k=8时选择的初始中心Fig.1 Initial center chosen by I-k-means-+ algorithm when k=8 此外, I-k-means-+算法中只有分裂簇与删除簇配对成功时, 才能提高聚类精度, 而I-k-means-+算法中每次迭代仅进行一次分裂簇与删除簇的配对, 且易出现配对失败的情况, 影响算法收敛精度. I-k-means-+算法的划分与删除簇步骤中通过随机选择分裂簇中的一个数据点作为新中心, 该方法的随机性较大且选择不同的新中心其解的收敛结果不同, 从而导致聚类结果的稳定性变差. 针对I-k-means-+算法聚类精度有待优化与聚类结果不稳定的问题, 本文提出一种基于min-max准则与区域划分的I-k-means-+聚类算法, 即MR-k-means-+算法(I-k-means-+clustering algorithm based on min-max criterion and region division). 算法提出min-max准则, 在式(3)中引入数据到最近中心的距离并计算数据点的权重, 选择权重最大的作为新的聚类中心, 以此避免初始聚类中心密集的情况. 当配对失败时重新选择分裂簇与原删除簇再次配对, 以提高配对成功率, 进一步提高聚类精度. 针对I-k-means-+聚类结果不稳定的情况, 本文算法通过多区域划分的策略选择多个候选中心, 以增加解的多样性, 从而提高聚类的精度与稳定性. I-k-means-+聚类算法的中心选择策略可能会导致初始聚类中心分布不均, 即存在多个中心聚集在同一簇中, 而有的簇没有聚类中心的问题. 从而降低初始解的精度, 导致算法的聚类精度较差. 为避免初始聚类中心分布不均的问题, 本文算法在新中心的选择中考虑了其他中心的分布情况. 若参与计算的中心数量过多, 虽能改善聚类中心的分布效果, 但极大降低了算法的效率. 本文提出min-max准则, 该准则选择新的聚类中心时, 会先计算每个数据点到最近中心的距离(minimum distance), 然后优先选择距离最大(maximum distance)的数据点作为新的聚类中心. 令Q(p,C)表示数据点p与中心集合C中各中心距离的最小值计算公式为 (6) 将Q(p,C)代入式(3)得到本文的中心评价公式为 V2(p,C)=V1(p,C)×α+Q(p,C)×β. (7) 如图2所示, 利用式(7)可较大程度地避免两个中心在同一个簇中的情况, 保证中心分布更均匀.与I-k-means-+初始化方法相比, 本文初始化方法在图1数据集上, 避免了多个中心聚集在同一个簇的情况, 选择的中心分布更均匀, 且初始解的精度较前者有较大提升. 此外, I-k-means-+初始化方法提出有用中心的概念是为减少初始化部分的计算量, 本文利用I-k-means-+算法已有的距离信息, 在不增加初始化方法时间复杂度的前提下改进其初始中心的选择策略, 并提高聚类精度. 在式(7)中通过参数α和β分别调整有用中心和最近中心在最终结果中所占的比例,α和β都在[0,1]内.当β=0时, 式(7)等价于式(3); 当α=0时, 式(7)等价于式(6). 为避免只选择一个随机数据点作为候选中心导致的聚类结果不稳定与精度较低的问题, 本文提出多区域划分的策略获取更多的候选中心, 通过增加解的多样性提高聚类精度与稳定性. 该策略将分裂簇Si中的数据点分割到不同的区域, 从每个区域挑选一个候选中心.分割区域的数量对本文算法的效率和精度有重要影响, 分割的区域过多, 会增加距离计算次数, 导致算法的时间复杂度过高; 分割的区域过少, 会降低算法的精度.因此, 需要在精度与时间复杂度之间做一个平衡.本文将分裂簇Si的数据点分割到两个不同的区域中, 第一个区域以中心Ci为圆心, 以Ci到簇内最远点距离的1/2为半径, 划分成一个圆形区域.在簇Si中, 除第一区域外的其他数据点作为第二区域的数据点, 然后分别在第一和第二区域中选择距离Ci最远的点作为候选中心M1和M2, 如图3所示.最后随机从Si中选择一个数据点作为第三个候选中心M3.与原算法只有一个候选中心相比, 该策略增加了解的多样性. 本文将Ci作为第一个中心, 依次从候选中心集中选出一个候选中心作为第二个中心, 然后使用簇Si中包含的所有数据点, 运行2-k-means(k=2的k-means算法)迭代一次, 选择分裂后SSE值最小的中心, 替换原来簇中心Ci和Cj.此时, SSE的下降幅度和迭代次数呈衰减趋势, 本文为节省迭代时间且能找到收敛效果较好的中心, 故2-k-means只迭代一次. I-k-means-+算法中仅进行一次分裂簇与删除簇的配对, 而配对的成功率对聚类精度有较大影响. 本文提出基于SSE的簇对再匹配方法, 当配对失败时重新选择分裂簇与原删除簇再次配对, 以提高配对成功率, 进而提高聚类精度. 本文在簇Si和Sj配对失败后, 即SSE(X,S′)>SSE(X,S), 重新选择增益最大的簇Sm(Sm≠Si), 再次执行划分Sm与删除Sj的操作, 并使用Hamerly[14]的方法收敛为解S″.若SSE(X,S″) MR-k-means-+算法整体流程如下. 输入: 数据集X, 聚类个数k; 输出: 解S; 步骤1) 簇的初始状态均设为允许划分与删除, 在数据集X中选择第一维度最小的数据点作为中心C1; 步骤2) 用式(7)计算每个数据点的权重V1(p,C), 选择权重最大的数据点为中心Cm(m=2,3,…,k-1), 并使用Hamerly收敛为解S; 步骤3) 选择增益最大的簇Si且该簇应允许划分, 若没有该簇或有k/2个簇的增益大于Si, 则结束; 步骤4) 在满足下列3个条件的簇中, 找到损失最小的簇Sj; 若没有, 则结束: ①Si≠Sj且Cost(Sj) ②Si与Sj可以配对且Si与Sj互不为邻簇[13]; ③Sj应允许删除; 步骤5) 若有k/2个簇的损失小于Sj, 则Si设为不可划分的簇, 并转步骤3); 步骤6) 设置C′=C后, 按多区域划分删除策略划分簇Si, 并选择候选中心M1,M2,M3, 将簇中心Ci作为第一中心, 分别将候选中心作为第二中心, 使用2-k-means迭代一次, 保留精度最高的一组替换Ci和Cj; 步骤7) 根据步骤6)的中心集C, 使用Hamerly将数据集X收敛为解S′, 若SSE(X,S)>SSE(X,S′), 则执行如下操作: ①Si和Sj标记为不可删除且设置Sj的强邻簇[13]为不可删除; ②S=S′且设置Si和Sj的强邻簇为不可删除; 步骤8) 若SSE(X,S) ① 找到增益最大簇Sz(Sz≠Si),C=C′并选择簇Sz中一个随机点替换Cj, 使用Hamerly收敛为解S″; ② 若SSE(X,S″) 步骤9) 若成功配对的数量大于k/2, 则算法结束; 否则, 重复执行步骤3)~9). 本文算法主要由三部分组成: 第一部分为基于min-max准则的中心选择策略, 该部分通过式(7)计算数据点的权重并选择初始聚类中心, 其时间复杂度为O(nkd+k2d); 第二部分为多区域划分删除策略, 其中划分阶段时间复杂度为O(lnd), 删除阶段时间复杂度为O(ld), 该部分时间复杂度为O(lnd); 第三部分为基于SSE的簇对再匹配方法, 该部分的时间复杂度为O(lkdn+lk2d).所以本文算法的时间复杂度为O(lkdn+lk2d), 其中l表示划分删除步骤的迭代次数,n表示样本数,k表示聚类中心个数,d表示样本维度. 实验环境配置为Intel(R) Core(TM) i5-6200U CPU @ 2.30 GHz 2.40 GHz, Windows10 64 位操作系统, 内存12 GB, VS 2013开发平台, 所有算法均使用C++语言编程实现. 为验证MR-k-means-+算法的有效性, 实验选用5个UCI数据集(https://archive.ics.uci.edu/ml/index.php), 将本文算法与其他3种算法进行性能对比. 选取数据集的信息列于表1. 表1 5个UCI数据集信息Table 1 Information of five UCI datasets 实验中的对比算法为k-means算法、 聚类中心初始化算法k-means++[15]、 I-k-means-+(IK-+)算法及本文的MR-k-means-+(MRK-+)算法. 为避免聚类中心数量过大导致的无意义聚类, 本文对数据个数小于1 000的k值设置为5,10,15,20, 数据个数大于1 000的k值设置为5,10,20,50. 本文算法参数设置:α=0.5,β=0.5. 为避免算法中聚类精度与运行时间的随机性, 所有算法均运行50次取平均值. 3.2.1 求解精度测试 算法的求解精度以收敛后的SSE衡量. 对于一个给定的算法, 为量化其相对于IK-+算法的精度提升效果, 其精度提升百分数U的计算公式可表示为 U=(E1-E2)/E1×100%, (8) 其中E1表示IK-+算法的目标函数值,E2表示对比算法的目标函数值. 不同算法在测试数据集上的运行结果列于表2. 由表2可见, 在20次对比实验中, 有16次本文算法是所有算法中精度最高的. 各优化算法精度提升百分数列于表3. 由表3可见, 与IK-+算法相比,k-means算法的精度平均下降了149.64%,k-means++算法下降了5.69%, 而本文算法的聚类精度与IK-+算法相比平均提升了6.47%, 当k=50时提升了18.6%, 本文算法有效提升了IK-+算法的聚类精度. 表2 不同算法在测试数据集上的运行结果Table 2 Running results of different algorithms on test datasets 表3 各优化算法精度提升百分数Table 3 Accuracy improvement percentage of each optimization algorithm % 3.2.2 稳定性测试 为测试聚类结果的稳定性, 本文采用方差进行衡量. 在不同数据集下, 将本文提出的MRK-+算法与IK-+算法使用不同k值分别运行50次, 并根据SSE计算不同k值下运行结果的方差, 其方差对比结果如图4所示. 由图4可见, 与IK-+算法相比, 除数据集Iris中k=10和k=20外, 本文算法的方差均可忽略不计. 在20次方差对比中, 其中有17次本文算法的方差优于IK-+算法, 并有2次方差相等, 表明本文算法与IK-+算法相比聚类结果更稳定. 图4 本文算法与IK-+算法的方差对比结果Fig.4 Variance comparison results between proposed algorithm and IK-+ algorithm 3.2.3 运行效率对比 令T1表示IK-+算法的运行时间,T2表示某个给定算法的运行时间, 则该算法相对于IK-+算法的时间加速百分数L计算公式为 (9) 图5为本文算法相对于IK-+算法的时间加速比结果. 由图5可见, 本文算法在k较小时速度提升明显,k较大时速度略有下降, 平均速度与I-k-means-+算法基本相当. 图5 本文算法相对于IK-+算法的时间加速比Fig.5 Time speedup ratio of proposed algorithm compared to IK-+ algorithm 综上所述, 针对I-k-means-+算法聚类结果不稳定, 并且求解精度有待提高的问题, 本文提出了一种基于min-max准则与区域划分的I-k-means-+聚类算法. 提出min-max准则, 以避免初始化中心过度密集的情况, 提高初始解的精度; 将分裂簇分割为不同区域, 从中选择多个候选中心, 增加解的多样性, 提高聚类结果的稳定性; 当配对失败后, 重新选择分裂簇与原删除簇再次配对, 以提高配对成功率, 进一步提高算法的求解精度. 实验结果表明, 与I-k-means-+算法相比, 本文算法与前者的运行效率基本相当, 聚类精度平均提升6.47%, 多次运行结果的目标函数值波动更小、 聚类结果更稳定.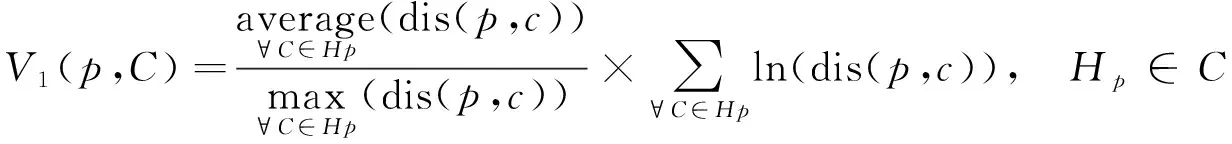
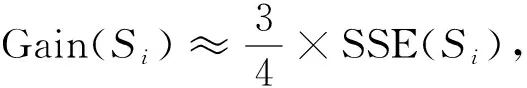
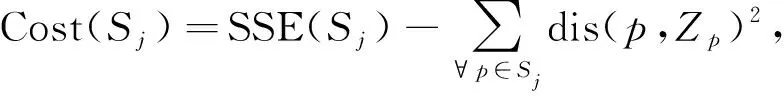

2 I-k-means-+算法的优化改进
2.1 基于min-max准则的中心选择策略

2.2 多区域划分删除策略
2.3 基于SSE的簇对再匹配方法
2.4 算法流程
2.5 计算复杂度分析
3 实 验
3.1 实验环境与数据

3.2 实验结果与分析