两类Heisenberg李超代数的标准上同调

江 薇, 远继霞

(黑龙江大学 数学科学学院, 哈尔滨 150080)

李超代数是李代数的自然推广, 广泛应用于数学和物理学的研究中. 目前, 关于上同调群的研究也备受关注. 文献[1]给出了李代数的标准复形; 文献[2]给出了有限群计算上同调的方法并对其举例说明; 文献[3]计算了李超代数系数取自平凡模的上同调; 文献[4]在李超代数上同调的基础上计算了李超代数相对上同调; 文献[5]给出了Heisenberg李超代数的相关结论; 文献[6]提出了混合上同调理论并在此基础上计算了glm|n的混合上同调.

Heisenberg李代数是一类重要的代数, 该代数及其表示论在Kac-Moody代数和物理学等领域应用广泛. 为研究物理学中的超对称性问题, 人们将Heisenberg李代数推广到Heisenberg李超代数, 并对其结构、 表示、 同调等理论进行了研究[7-11].

本文计算4维偶中心Heisenberg李超代数与3维奇中心Heisenberg李超代数系数取自1维平凡模的标准上同调. 首先, 计算两类Heisenberg李超代数上同调的微分算子; 其次, 计算这两类Heisenberg李超代数的标准上同调, 并得到其基底与维数.

1 预备知识

其中α∈2.则Hom(V,W)和V⊗W均为超空间.定义映射:

τV,W:V⊗WW⊗V,

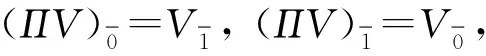
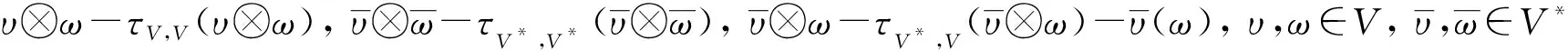
定义1[6]设D是V的一个子超空间, 且

Λ={i|1≤i≤m}∪{m+j|1≤j≤n},

且有

其中A∈g.设{Xa|a∈Λ}为Πg*关于{Ea|a∈Λ}的对偶基.定义映射Γ:

Γ: g→Der(S(Πg*)),

定义2[12]设

其中Γa=Γ(Ea), 验证可得δ2=0, 于是有如下微分复形:

2 h2,1的标准上同调

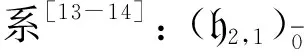
设Λ(ξ1,ξ2,…,ξn)是具有n个变元ξ1,ξ2,…,ξn的外代数.设X1,…,X4是E1,…,E4的对偶基, ∂i是Xi对应的导子, 其中i=1,2,3,4.为方便, 给出C0(h2,1,)及其元素v的形式:

C0(h2,1,)≅[X1]⊗Λ(X2,X3,X4)⊗.

令t∈,s=(s1,s2,s3), 其中si∈{0,1},i=1,2,3.C0(h2,1,)中的任意元素v都可写成如下形式:

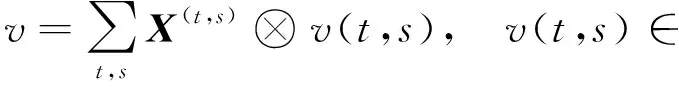
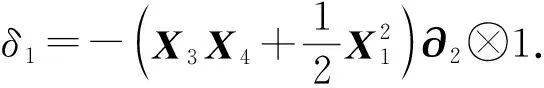
定理1h2,1系数取自1维平凡模的标准上同调为

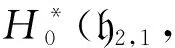
该标准上同调的基底为{1,X3,X4,X3X4,X1,X1X3,X1X4,X1X3X4}, 维数为8维.

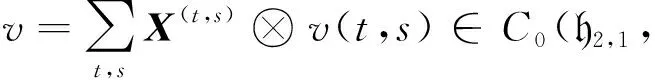
首先, 证明

Kerδ1=[X1]⊗Λ(X3,X4)⊗.

(2)

通过计算知“⊇”显然成立, 下面证明“⊆”成立.设v∈Kerδ1, 则δ1(v)=0.由式(1)可知, 对任意的t, 当t≥0时均有v(t(1,s2,s3))=0成立, 其中s2,s3∈{0,1}, 从而

即式(2)成立.

其次, 证明

由式(1)可知

其中s2,s3∈{0,1},t∈,a∈, 从而

因此

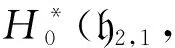
证毕.

3 ba1的标准上同调

设Y1,…,Y3是F1,…,F3的对偶基, ∂i是Fi对应的导子, 其中i=1,2,3.为方便, 给出C0(ba1,)及其元素v的形式:

C0(ba1,)≅[Y1,Y2]⊗Λ(Y3)⊗.

令t=(t1,t2),t∈2,s∈{0,1}.C0(ba1,)中的任意元素v均可写成如下形式:

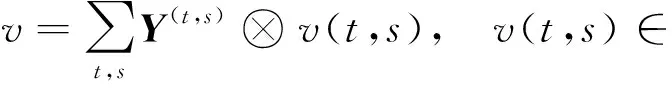
由计算可得ba1上同调的微分算子为δ2=-Y2Y3∂1⊗1.下面计算ba1系数取自1维平凡模的标准上同调.

定理2ba1系数取自1维平凡模的标准上同调为

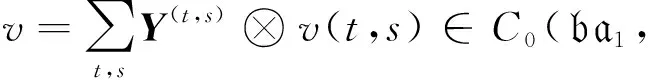
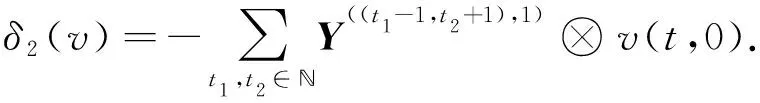
(3)

首先, 证明

Kerδ2=([Y1,Y2]⊗Y3⊕[Y2])⊗.

(4)

通过计算知“⊇”显然成立, 下面证明“⊆”成立.设v∈Kerδ2, 则δ2(v)=0.由式(3)可知, 对任意的t1, 当t1≥1时均有v(t,0)=0成立, 从而

即式(4)成立.

其次, 证明

Imδ2=Y2[Y1,Y2]⊗Y3⊗.

由式(3)可知

δ2(Y(t,1)⊗a)=0,δ2(Y(t,0)⊗a)=-Y((t1-1,t2+1),1)⊗a,

其中t∈2,a∈, 从而

Imδ2=span{Y((t1-1,t2+1),1)⊗a|t1,t2∈,a∈}=Y2[Y1,Y2]⊗Y3⊗.

因此

证毕.