粗糙核Marcinkiewicz积分在Morrey-Adams空间上的有界性
2023-09-27朱小杰陶双平
朱小杰, 陶双平
(西北师范大学 数学与统计学院, 兰州 730070)
1 引言与主要结果
设Ω为n上的零次齐次函数, 满足以下消失矩条件:
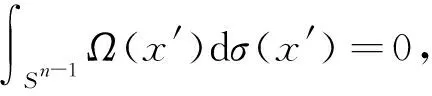
(1)
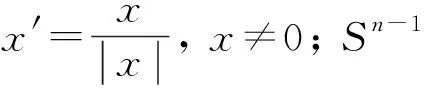
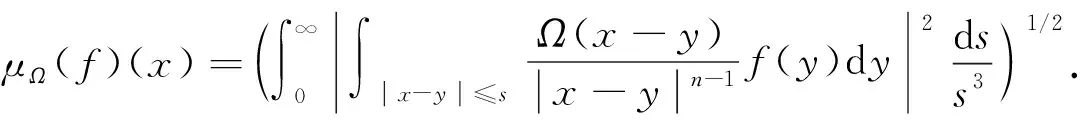
(2)
设b是一个局部可积函数, 则由μΩ和b生成的交换子定义为
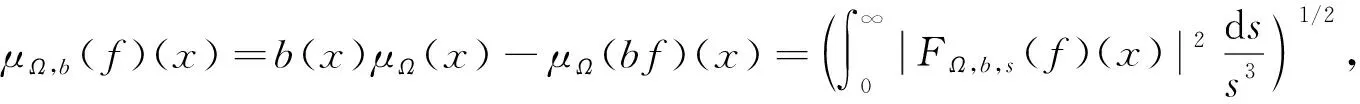
(3)
其中
Marcinkiewicz[1]首次提出了一维Marcinkiewicz算子:
其中

之后, Zygmund[2]证明了μ在Lebesgue空间Lp()(1 定义1[7]设0≤λ≤n, 1≤p<∞, Morrey空间定义为 其中B(x,r)={y∈n: |x-y| 定义1中的Morrey范数‖·‖Lp,λ可写成如下形式: 定义2[13]设1≤p<∞,λ∈, 1≤θ<∞, Morrey-Adams空间定义为 为讨论Marcinkiewicz积分算子的交换子μΩ,b在Morrey-Adams空间上的有界性, 需介绍粗糙核极大算子MΩ: 当Ω∈L1(Sn-1)时, 算子MΩ在Lp空间上是有界的, 其中p>1. 定义3[14]BMO空间定义为 定义4[14]设0<β<1, Lipschitz空间定义为 本文的主要结果如下. (4) 定理3设b∈BMO(n),Ω∈Ls(Sn-1)(1 引理2[15]设f∈BMO(n), 则对n中的任意球B和1 |μΩ,bf(x)|≤CΩ‖b‖Lipβ(MΩf(x))ν‖f‖1-ν, 证明: 固定x∈n,R>0, 记f=f1+f2, 其中f1=fχB(x,R),f2=fχB(x,R)c.利用μΩ,b的线性性质, 有 |μΩ,bf(x)|≤|μΩ,bf1(x)|+|μΩ,bf2(x)|∶=A+B. 对于A, 由Minkowski不等式, 得 从而有 由文献[16]中引理4.1的方法可得 这里CΩ是指仅依赖于Ω的正常数.证毕. 设z∈n, 任意给定球B(z,2r)(r>0), 把f分解为f=f1+f2, 其中f1=fχB(x,2r),f2=fχB(x,2r)c,f的分解依赖于r.于是 对于G, 由μΩ在Lp(n)空间上的有界性, 易得 对于H, 注意到当x∈B(z,r),y∈B(z,2r)c⊂B(x,r)c时, 有 因此 对于I1, 注意到|x-y|≈|z-y|, 结合中值定理, 有 再由Minkowski不等式, 得 对于I2, 同理有 注意到如果y∈B(z,2r)c, 则y∈B(x,2jr)B(x,2j-1r)(j≥1), 因此可得 再利用球坐标变换, 有 由Hölder不等式, 得 所以 令t=2j+1r, 由Minkowski不等式, 可得 固定z∈n, 由引理3得 由已知条件(4)得 定理2证毕. 设z∈n, 对任意给定球B(z,2r)(r>0), 把f分解为f=f1+f2, 其中f1=fχB(x,2r),f2=fχB(x,2r)c,f的分解依赖于r.于是 对于Q, 由μΩ,b在Lp(n)空间上的有界性, 易得 对于P, 由定理1的证明, 可得 对于J1, 有 令t=2j+1r, 由引理2, 得 对于J2, 有 注意到当b∈BMO(n)时, 有|bB(z,2j+1r)-bB(z,r)|≤C(j+1)‖b‖*, 则 对于J22, 由Hölder不等式, 得 令t=2j+1r, 由Minkowski不等式, 得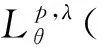


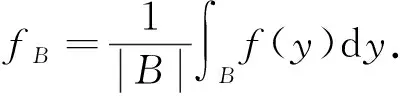
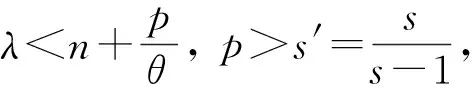

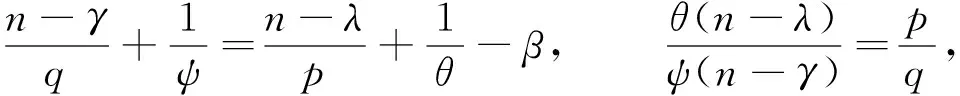
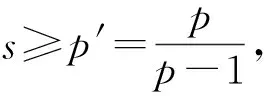
2 主要结果的证明
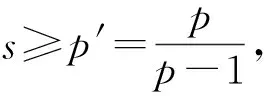
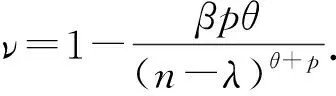
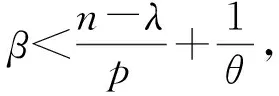
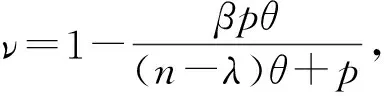
2.1 定理1的证明

2.2 定理2的证明


2.3 定理3的证明

