不同作用点下压电测力仪灵敏度规律及其预测
2023-09-27张军甄田甜蔡佳乐李孟曈刘禹廷
张军, 甄田甜, 蔡佳乐, 李孟曈, 刘禹廷
(大连理工大学 高性能精密制造全国重点实验室,辽宁 大连 116000)
1 引 言
在核电工程、航空航天、城市建设、工业制造等领域应用的重型装备力载荷可达数十千牛甚至更大,利用多点支撑式测力仪对重载装备运行过程中的力载荷进行精准测量,能够保证装备使用过程中的安全性和可靠性[1-2]。重型制造装备通常有着大载荷、大惯量、多自由度、变作用位置等特点[3],测力仪在不同测试位置的输出准确性与该位置灵敏度相关。
测力仪器的灵敏度是指在稳定工作状态下输出变化量与输入变化量的比值,能反映测力仪器对输入信号的放大程度,直接关系到测力仪器的测量精度和可靠性[4]。仪器的灵敏度作为一项重要的精度评价指标,在材料测试、质量控制、压力检测等领域都备受关注[5-6]。汪思琦等人对压电传感器的灵敏度进行分析,设计灵敏度标定装置,研究了压电传感器灵敏度的影响因素[7];刘俊等利用解析数学模型对垫圈式压电六维力传感器的灵敏度进行了解析[8];马奕萱等在研制四支点压电测力仪时发现了测力仪在不同加载点下输出电压值存在差异,证明测力仪在变作用位置时灵敏度不同,但无法获得具体加载位置对应测力仪灵敏度值[9]。测量大量程矢量力时,测力仪输出差异性问题更加显著。为实现变作用位置大载荷的精确测量,须已知作用面域内测力仪任意位置的灵敏度以准确计算待测力大小,故需对不同作用点下多点支撑式压电测力仪的灵敏度进行研究分析。李克等人应用灰狼优化算法确定最小二乘支持向量机的最优核参数和正则化参数,提高预测模型对无轴承感应电机磁链特性的预测精度,最大绝对误差为0.000 064,该模型的预测精度很高[10]。基于刚体假设对测力仪不同作用点下的灵敏度可以进行计算推导,但由于实际工况中测力仪发生复杂变形,计算结果与真实值存在较大偏差且难以进行补偿,通过优化模型对变作用点下测力仪的灵敏度进行精准预测则可以规避该问题。
本文为解决八支点测力仪的灵敏度随待测矢量力作用点变化规律复杂难以进行计算的问题,设计了分别基于灰狼算法(Grey Wolf Optimization, GWO)、遗传算法(Genetic Algorithm, GA)和蚁群算法(Ant Colony Optimization,ACO)三种优化算法下的LS-SVM预测模型,对不同作用点下测力仪的灵敏度进行回归预测,通过比较预测结果偏差,选择最具可靠性的预测算法模型。
2 测力仪灵敏度理论计算
2.1 测力仪力学分析模型
八支点压电测力仪主要由上、下压板和八个测力单元构成,如图1,测力单元在圆周上均匀分布。

图1 八支点测力仪结构Fig.1 Structure of eight-pivot piezoelectric
根据静力学原理,测力仪受到力的作用时,会将受力分配至各测力单元,力学分配模型如图2所示。测力单元距中心的距离为,矢量力作用点坐标为(d,e),将测力单元按逆时针方向编号为1~8号。

图2 测力仪受力几何描述示意图Fig.2 Schematic diagram of the force geometry of dynamometer
将测力单元对上板的支撑等效为测力单元上表面中心点对上板的支撑,每个支撑点对上板的支撑方式为铰支,基于刚体假设,推导测力单元的力学分配关系式。以编号为1的测力单元为例推导三向受力公式,如式(1)~式(3)所示,其余七个单元以此类推。
其中:表示编号为i的测力单元在j方向的受力,式中j=x,y,z,i=1;m,n表示测力单元与坐标轴距离;e,d表示矢量力作用位置与坐标轴距离。
2.2 不同作用点下测力仪灵敏度推导
根据力电转换原理,测力单元受力输出相应电荷,利用电荷放大器将电荷转换为电压,测力仪各方向总输出电压与该方向测力单元输出电压总和相等,即:
其中:j表示X,Y,Z三个方向,i表示编号为i的测力单元,i=1,2,…,8;Uj表示测力仪受力时在j方向输出的电压;kji表示编号为i的测力单元在j方向上的力电转换系数。
根据灵敏度定义,测力仪的灵敏度为:
其中:Sj表示测力仪在j方向的灵敏度。将式(4)和式(5)代入推导的力学分配模型,得到不同作用点下测力仪三向灵敏度理论计算值,如式(8)所示:
根据灵敏度计算公式,当矢量力作用位置发生变化时,由于八个测力单元自身力电转换系数存在差异,不能在公式中提出公因子。测力仪灵敏度随力作用位置变化规律复杂,难以进行计算和补偿。
3 测力仪变加载点实验
3.1 主向变加载点实验
由于实验装置结构限制,无法细分加载点。以Z方向为主向,在测力仪有效工作面域内设计25个加载点,如图3所示,各加载点间距均为50 mm。

图3 主向加载点示意图Fig.3 Schematic diagram of main loading point
实验装置主要包括液压加载装置、信号传输及采集系统及上位机软件三部分,如图4,信号传输和采集主要使用电荷放大器和数据采集卡。

图4 实验装置及信号传输过程Fig.4 Experimental device and signal transmission process
进行阶梯加载实验,加载的满量程为5 kN,阶梯为1 kN。每个加载点重复三次实验取平均值,线性度和重复性误差均低于1%,向间干扰低于3%,根据CIRP推荐标准草案[11],均满足精度要求。计算各加载点灵敏度,如表1所示。

表1 测力仪主向变加载点实验灵敏度/(mV·N-1)Tab.1 Sensitivity of dynamometer with changed position
将测力仪的主向灵敏度拟合为图像,如图5所示,测力仪第二象限灵敏度相对较高,第四象限较低,最大灵敏度差值为0.25 mV/N。

图5 测力仪主向变加载点实验灵敏度示意图Fig.5 Schematic diagram of sensitivity experimental
3.2 侧向变加载点实验
对测力仪的侧向进行变加载点实验,加载点位置示意图如图6所示。侧向加载点均布于测力仪上板中心线上,间距为50 mm,其中X1~X5位于Y轴上,用于测力仪的X向变加载点标定,Y1~Y5位于X轴上,用于测力仪的Y向变加载点标定。
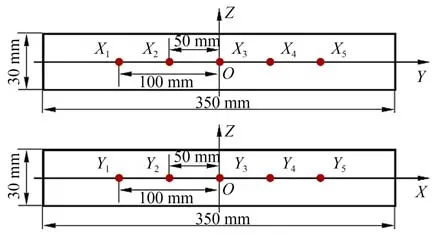
图6 侧向加载点示意图Fig.6 Schematic diagram of lateral loading point
侧向变加载点实验加载满量程为3 kN,以0.6 kN为阶梯,重复三次实验取平均值,线性度、重复性及向间干扰均满足精度要求。灵敏度如表2~表3所示。

表2 测力仪X向变加载点实验灵敏度Tab.2 Sensitivity of dynamometer with changed position

表3 测力仪Y向加载点实验灵敏度Tab.3 Sensitivity of dynamometer with changed position
X,Y方向灵敏度随加载点坐标变化如图7所示。

图7 测力仪侧向变加载点实验灵敏度示意图Fig.7 Schematic diagram of lateral loading point

图8 不同作用点下测力仪的灵敏度预测流程图Fig.8 Flowchart of changed position sensitivity prediction
测力仪X向灵敏度随坐标值增大而减小,最大灵敏度差值为0.47 mV/N;测力仪Y向灵敏度随坐标值先增大后减小,最大灵敏度差值为0.22 mV/N。
3.3 灵敏度实验值与理论值偏差
将变加载点实验设计的主、侧向加载点坐标代入理论计算公式,得到各加载点灵敏度理论值。定义灵敏度实验值与理论值之间的偏差为e:
其中:St表示理论灵敏度,Se表示实验灵敏度值。定义偏差值标准差为σej:
理论计算是基于刚体假设进行的推导,且代入的测力单元力电转换系数是通过对单元进行标定得到的,标定时测力单元受力点为中心位置。由于测力仪上板约束复杂,对其施加外力时会发生复杂变形,导致测力单元受力点偏离中心位置,力电转换系数随测力仪受力点位置改变发生规律不可寻的变化,故不同作用点下测力仪灵敏度的实验值与理论值偏差较大。如表4所示。

表4 灵敏度计算偏差及其标准差Tab.4 Calculation error and standard deviation of sensitivity
测力仪在投入使用前,对测力仪多位置进行变加载点实验可以获取其不同作用点下灵敏度值。但加载实验只能保证以mm为单位进行加载点变动,无法获取任意连续作用点下测力仪灵敏度。
4 基于LS-SVM算法的灵敏度预测
4.1 预测算法模型设计
设计基于最小二乘向量机(LS-SVM)的算法预测不同作用点下测力仪的灵敏度。将实验数据输入预测模型对其进行训练,能够预测连续任意作用点下测力仪的灵敏度。利用加载位置灵敏度的预测值可以反推待测力,保证测力仪对变作用位置大量程矢量力的测试精度。LSSVM将复杂问题转化为线性方程组求解[13],其RBF径向基核函数如式(11)所示:
其中:xi为输入量,σ2为平方带宽。影响LSSVM预测精度的主要参数为平方带宽σ2和正则化参数γ,利用三种优化算法:遗传优化算法(GA)、蚁群优化算法(ACO)和灰狼优化算法(GWO)对两个参数进行迭代寻优。当适应度值满足要求时,将待预测位置的坐标输入模型,输出该位置下测力仪的灵敏度预测值。
4.2 预测算法模型验证
设置参数寻优范围为γ∈[0.01,10],σ2∈[0.1,100]。分别训练基于三种优化方法的灵敏度预测函数,利用预测集数据对预测算法模型进行验证。预测结果与真实值对比如图9~图10所示。

图9 主向灵敏度预测结果Fig.9 Prediction of main direction sensitivity

图10 侧向灵敏度预测结果Fig.10 Prediction of lateral direction sensitivity
对比基于三种优化方法的预测值与真实值,求出偏差平均值及其标准差,如表5所示。分析数据并绘制如图11所示的示意图对预测偏差进行表征。
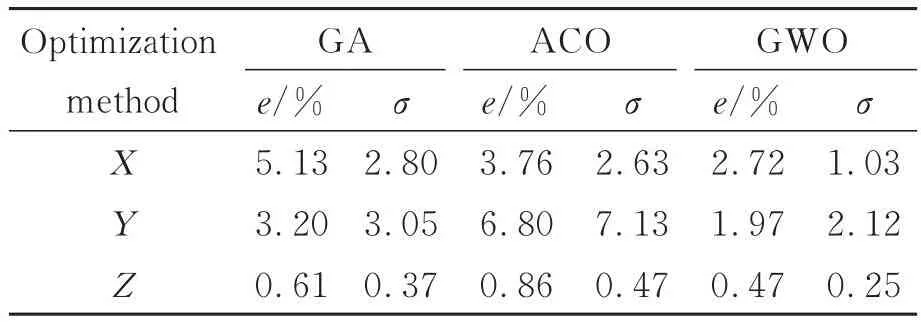
表5 灵敏度预测偏差及其标准差Tab.5 Prediction deviation and standard deviation of sensitivity
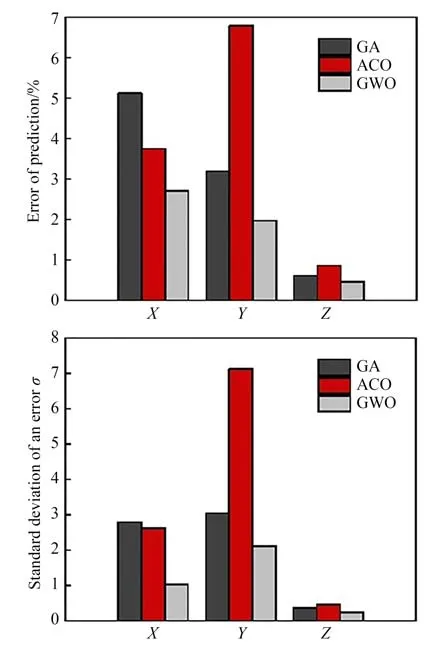
图11 灵敏度预测偏差及其标准差Fig.11 Prediction deviation and standard deviation of sensitivity
综合预测结果,基于GWO-LSSVM算法预测的不同作用点下测力仪的灵敏度平均偏差及其标准差在三个方向上均相对较小,可靠性更高,能够准确预测不同作用点下测力仪的灵敏度。
5 结 论
本文根据现代工业大型装备矢量力载荷大量程、高精度的测试要求,提出了测力仪变作用位置的灵敏度理论计算方法,并对比了理论计算与实验结果之间的偏差。基于优化方法利用变加载点实验结果对LS-SVM算法模型进行了训练,对比三种优化方法下的灵敏度预测偏差,得到最具可靠性的预测算法模型。实验验证表明:不同作用点下测力仪的灵敏度预测模型的平均预测偏差小于3%,偏差的标准差小于2.5%。其中主向预测平均偏差仅为0.25%,侧向预测平均偏差较大的原因是训练数据较少,增加训练集数据可进一步提高预测精度。
