基于模糊聚类-马尔可夫链的换电站负荷预测模型
2023-09-27范明康张怡康健余洋
范明康, 张怡,康健,余洋
(1.华北理工大学电气工程学院, 河北省唐山市 063210;2.新能源电力系统国家重点实验室(华北电力大学),河北省保定市 071003)
0 引 言
在节能减排的大环境下,电动汽车(electric vehicle,EV)渗透率不断提高,换电站极大节省了EV用户充电时间,EV换电站被纳入国家新基建计划,数量也不断攀升[1]。2022年,国家下发了《关于进一步提升电动汽车充电基础设施服务保障能力的实施意见》,提出完善新能源汽车储放绿色电力的调度机制[2-3]。换电站(battery-swap station,BSS)电池是一类优良的可调度资源,能为电网调度提供可观的调度潜力,合理调度BSS电池进行充放电可以减小其对系统的影响[4]。但是,EV用户换电需求具有随机性[5-6],预测其换电需求,并建立准确的BSS负荷预测模型是BSS参与电网调控的重要工作。
目前,针对EV用户换电需求预测方法,已有学者开展了一些研究。文献[7]将换电储备阈值作为影响EV换电需求规律的因素,为BSS电池储备决策、分析负荷对电网的影响等提供了参考,但未考虑出行链因素。基于文献[7],文献[8]通过调查传统燃油车的出行链数据计算特征参数,以此预测EV用户的出行特征参数,进而构建需求预测模型,但燃油车的数据难以与EV数据高度贴合导致该研究结论具有局限性。文献[9]借鉴文献[8]的思路将EV用户依据使用习惯、属性和特征进行聚类,进一步建立基于出行链模拟的预测模型,不过文献[9]分析换电需求时未考虑路网影响。文献[10]在文献[8-9]的基础上,从路网与选站决策的角度对换电需求进行分析,对多信息互联下的EV行驶路径、运营状态等进行模拟,计算得到EV用户在各时段的换电需求。上述文献考虑了交通、电力、信息通信系统对规律性换电需求的影响,但是上述文献均是基于大量数据开展研究的,对于小样本或缺乏数据的场合难以达到较好的预测效果。而适用于小数量的泊松分布已被广泛应用于排队问题[11],通过少量数据即可获得BSS的换电需求。
在BSS负荷预测方面,文献[12]在满足换电需求的约束下,建立了以充电费用最低及日负荷曲线波动最小为目标的优化模型,但该模型在研究EV随机性时,未考虑换电需求的不确定性。文献[13]在文献[12]的基础上考虑了换电需求不确定性,采用蒙特卡洛模拟法计算换电站的可控容量,但蒙特卡洛算法运行速度较慢,且无法建立面向控制的模型。文献[4]针对文献[13]的问题建立了电池组的状态矩阵,对其进行分群,运用递推的思想计算电池组的负荷,该方法提升了运算速度,但是该研究对于电池组状态分群做出了过多的假设,且计算过程过于繁琐。文献[14]依据电池荷电状态(state of charge,SOC)对EV集群进行了人为分区,以实现可控容量预测,但是人为分区的主观性较强,由此影响了预测精度。文献[15-20]从经济优化调度的角度建立模型,但无法直接应用于调频、调峰控制。基于马尔可夫链的建模方法能够建立面向控制的模型,还能较为精确地描述系统结构随时间的变化情况[21],该方法已被应用于温控负荷及EV的聚合建模,如文献[22-25]计及温控负荷的异质性,将温度变化范围离散化,建立马尔可夫链模型,文献[26-29]构建了基于马尔可夫链的EV充放电负荷聚合建模方法。但是当前基于马尔可夫链的聚合建模方法大都以SOC的人为分区为前提,使得构建的聚合模型准确性不高。
此外,在进行BSS负荷预测建模前,若能根据SOC、电池容量等参数对电池进行预先分类,将有利于提升预测模型的准确性。模糊C均值算法(fuzzy-C-means,FCM)具有良好分配处理簇与簇之间边界点的能力,已被应用于EV充电类型分类等领域。文献[30]利用FCM算法对EV的充电类型以及该类型所对应的充电功率进行划分,将进入充电状态的EV分为7种类型,并根据各充电类型分配相应的充电功率,完成日负荷建模。为此,本文拟先采用FCM算法根据SOC对BSS中的电池组进行聚类,以便于建立高精度模型。
基于上述分析,本文对BSS负荷预测展开研究,以电动出租车为研究对象,提出基于泊松分布的EV换电需求预测方法,得到各时刻EV换电需求数量;在此基础上,利用自适应FCM依据SOC对BSS中电池集群进行自适应分区,方便定义BSS各电池的运行状态,并且降低状态空间的维数,避免人为分区的主观性;在分区后,针对BSS的充放电周期与EV充放电过程类似的特点,进一步利用马尔可夫链建立状态转移矩阵,并最终构建基于模糊聚类-马尔可夫链的BSS负荷预测模型。算例仿真表明,泊松分布准确预测了EV需求数量,相较于蒙特卡洛模拟法,本文建立的模型能更准确地预测BSS电池的充放电功率。
1 EV换电需求预测
泊松分布是统计与概率学中常见的离散机率分布,已被广泛应用于排队问题[31]。由于EV到达BSS换电与排队问题非常相似,故可合理假设EV到达BSS属于泊松过程。
将每个EV到达BSS的时间看作一个独立事件。第一辆EV到达BSS的时间被看作为第一个事件,记为t1,以此类推,第N辆EV到达BSS的时间被看作为第N个事件,记为tN。当N>1时,第N-1辆和第N辆EV的到达时间间隔可表示为hN。则tN可以表示为:
tN=t1+t2+…+hN,(N=2,3,…)
(1)
由于每个EV到达BSS的时间是一个独立变量,时间间隔也是一个独立的随机变量。记Yt为t时刻为止到达BSS进行换电服务的EV数量,遵循参数为λ的泊松分布,即:
(2)
式中:λ表示单位时间内EV到达BSS的次数。
R(t)=[r1,r2,r3,…,rN]
(3)
式中:rω是在ω时段进入BSS的EV数量;R(t)是总换电期间的电动汽车数量。
(4)
(5)
式中:ω为根据实际情况划分的换电时区数量;Ld是总换电时区的长度;Lstep是换电时区的单位长度。
相比文献[8-10],本文所提预测方法只需BSS运营时段进行换电数量的总数,无需路网、通信系统等数据。由式(2)可预测t时刻进行换电的EV数量。BSS换电过程中电池总量保持不变,每个换电时区储备的可供更换电池数需要大于换电需求电池数。
(6)
2 电池集群模糊聚类
2.1 FCM工作原理
给定数据集S={s1,s2,…,sn}表示BSS电池的SOC,FCM就是将数据集S划分为C个模糊集Ai(i=1,2,…,C)且2≤C≤n,即利用电池SOC大小作模糊聚类。C个模糊集的中心集合表示为v={v1,v2,…,vn}。FCM的目标函数如下:
(7)
式中:uij表示第j个数据点属于模糊集Ai的隶属度;dij表示数据点与模糊集中心之间的欧氏距离;m是模糊加权数。
FCM算法就是找到使目标函数最小的每组模糊集中心[32]。通过不断优化迭代建立隶属度矩阵和模糊集中心矩阵,根据矩阵中每个数据点中的最大隶属度值uij,将数据唯一划分到模糊集Ai中,完成BSS电池的划分。
2.2 电池集群自适应FCM
若采用FCM算法对BSS电池进行聚类,需要预先确定C的数目,对于C的选取存在人为主观性。本文借助自适应FCM,通过给定C的自适应函数有效避免此问题。
聚类的目的就是将数据分类,并使模糊集间的距离尽可能大,而模糊集内的数据点距离尽可能小,基于该思想,给出C的自适应函数。
首先,确定总体数据的中心:
(8)
然后,设计C的自适应函数:
(9)
式中:sj表示数据点;vi表示模糊集中心;函数L(C)的分子表示模糊集之间的距离,分母则表示模糊集内的数据点与该模糊集中心之间的距离。故L(C)的结果越大,表明分类越合理,即对应L(C)值最大的C为最佳值。算法实现流程见图1。
利用自适应FCM算法对电池集群进行聚类避免了在选择聚类数时存在的主观性,提高了实用性。
3 BSS负荷预测建模
BSS中的电池具有充电、放电和等待三种状态,等待状态下的电池无充放电功率,充电过程和放电过程具有互逆性,建模方法类似。为此,以充电过程为例详细分析BSS电池在充电状态下的建模过程。
3.1 充电过程的马尔可夫性描述
当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态,也就是说,系统的下一个状态只与当前状态信息有关,与更早之前的状态无关,那么这个随机过程具有马尔可夫性[33-34]。设{Xt,t≥1}为一个随机过程,则可表述为:
(10)
具有马尔可夫性的随机序列X={X0,X1,…,Xt,…}称为马尔科夫链,或马尔可夫过程。条件概率分布P(Xt|Xt-1)称为马尔可夫链的转移概率分布,转移概率分布决定了马尔可夫链的特性。
对于单个电池,其充电模式下的SOC可表示为:
(11)
式中:S(t+1)和S(t)分别表示t+1时刻和t时刻的SOC;Pc表示充电功率;ηc表示充电效率;Bs为电池实际容量;Δt为时间间隔。
根据式(11),电池SOC可以被认为是一个离散的随机过程,满足以下特性:S(t+1)的概率分布与电池的历史状态无关,只取决于电池在t时刻的状态,即符合马尔可夫链。
3.2 状态转移矩阵的确定
马尔可夫链确定了在不同状态之间的一系列转换中,两个或多个保持相同状态的状态之间改变SOC的概率。这种状态的变化可以发生在连续的两个状态之间,也可以不发生,而模糊化只决定如何定义状态。
通过自适应FCM算法可以得到数据点对应的隶属度矩阵,如式(12)所示,依据隶属度矩阵进行数据点划分。
(12)
根据隶属度最大原则,将SOC序列中的数据点唯一划分至C个模糊集Ai(i=1,2,…,C)中。若t时刻A1模糊集中包含n1个数据点,假设t+1时刻有n2、n3、n4个数据点分别转移至A2、A3、A4,并满足n1=n2+n3+n4,那么,从A1转移到A2的概率可表示为P1,2=n2/n1。同理可得,P1,3=n3/n1;P1,4=n4/n1。图2给出了从A1转换到其他状态的马尔可夫链逻辑状态转移示意图。
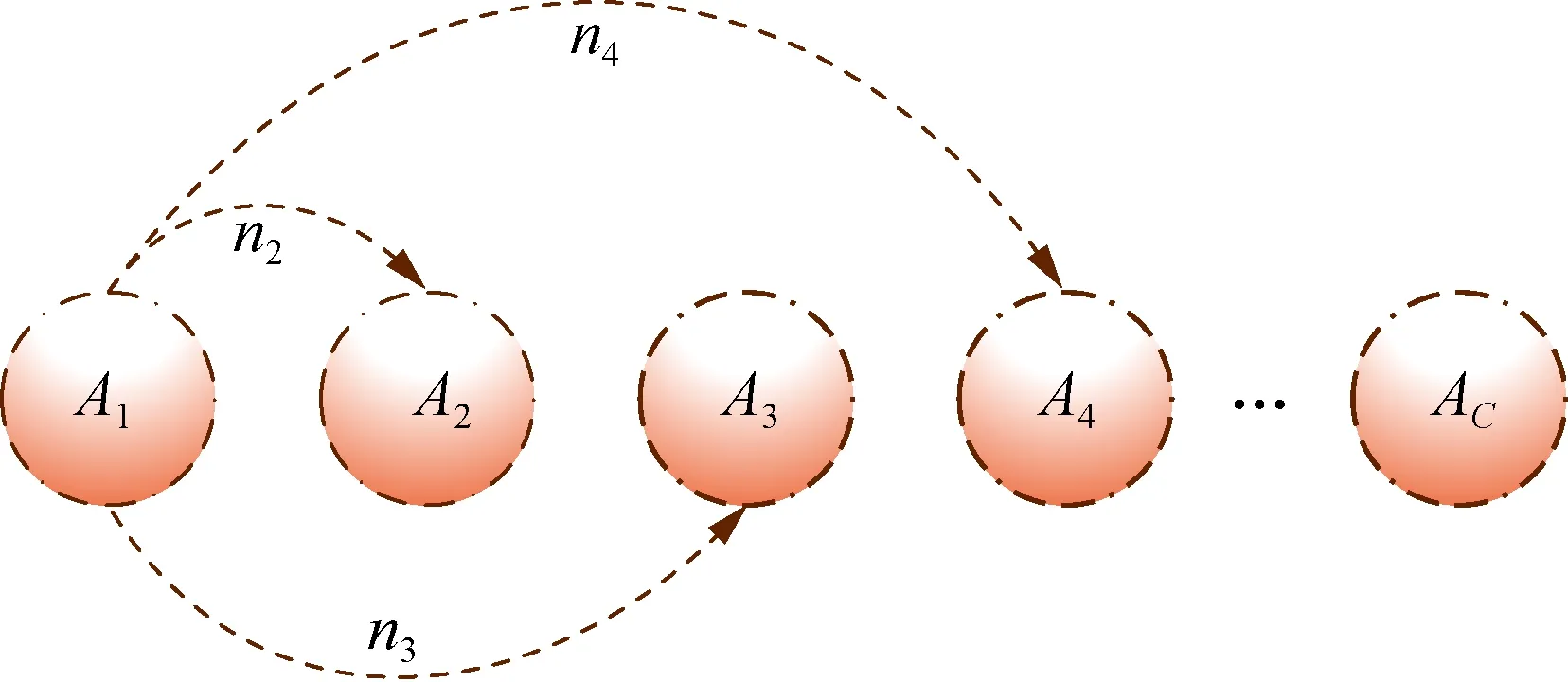
图2 状态转移图Fig.2 State transfer diagram
其他模糊集中数据点的转移同图2情况类似,故可以得到整个系统的状态转移矩阵。若从Ai模糊集到所有其他模糊集的转换总数用Ti表示,从Ai模糊集到Ak模糊集的单个状态转换用Tik(i,k=1,2,…,C)表示,则马尔可夫链转换概率矩阵可以写为:
(13)
(14)
3.3 BSS充电负荷预测模型
由于本文所建模型面向调峰、调频控制,其时间步长很小,所以假设一个时间步长内处于Ai的负荷只发生两种转移情况:保持原状态或者转入相邻状态。图3给出了SOC各模糊集的充电负荷动态转移示意图,阴影部分表示该模糊集的负荷量。每个模糊集的负荷净变化量为流入和流出该模糊集的负荷量差值,负荷净变化量不仅与相邻模糊集互动引起的负荷变化量相关,还与换电需求引起的负荷变化量有关。
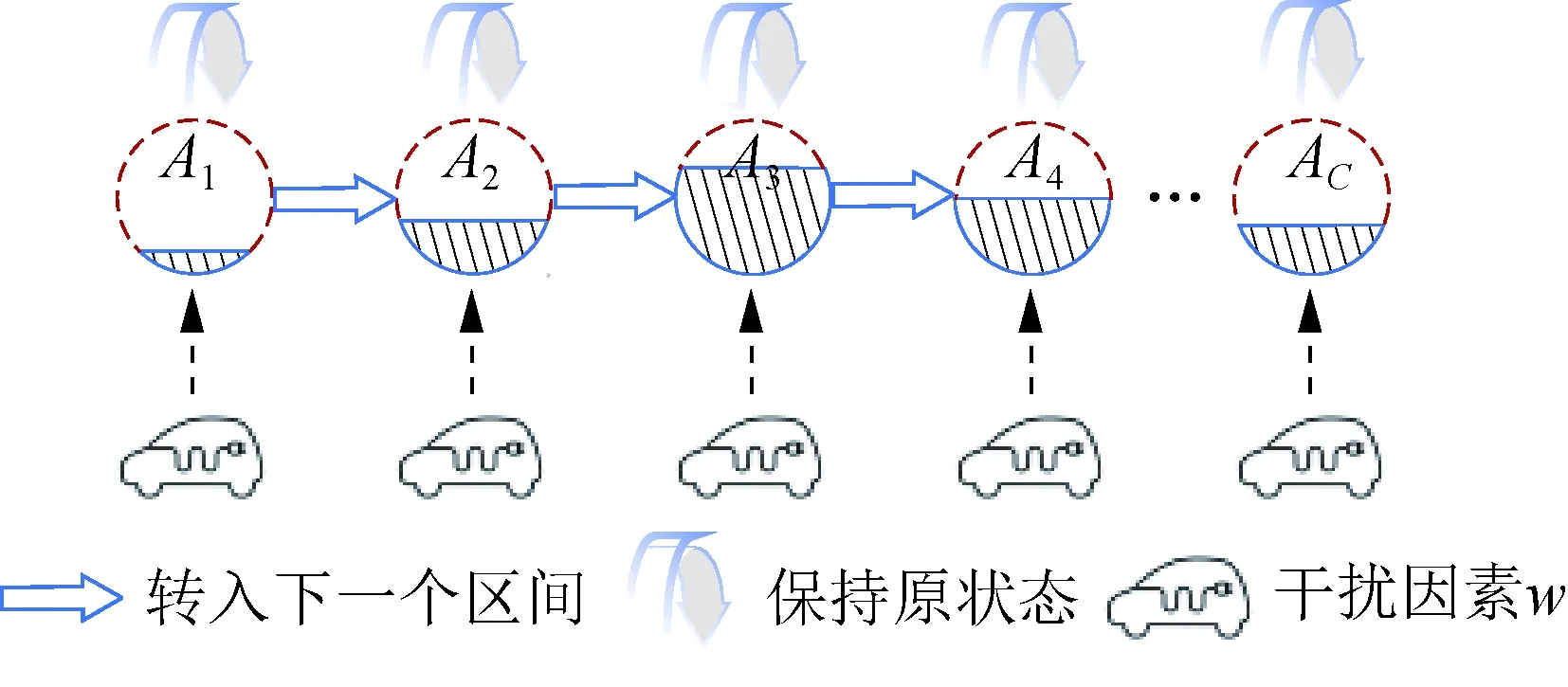
图3 动态转移过程示意图Fig.3 Schematic diagram of dynamic transfer process
不同状态下负荷量动态变化过程可由下式表示:
(15)
(16)
式中:xch(t,Ai)表示t时刻Ai模糊集内电池数量;xch(t+1,Ai)表示t+1时刻Ai模糊集内电池数量;Δxch(t,Ai)为t时刻从Ai转出的电池数量;Δxch(t,Ai-1)为t时刻从Ai-1转入Ai的电池数量;Pi,k为转移概率;wch(t,Ai)表示换电需求量。
整理式(15)和式(16),可得:
(17)
式中:αik表示动态转移矩阵的元素。进一步整理式(17),可以得到线性状态空间表达的电池集群充电负荷预测模型:
(18)
式中:xch(t)=[xch(t,A1),xch(t,A2),…,xch(t,AC)]T;wch(t)与xch(t)结构一致,也为C维列向量;ych(t)为t时刻电池集群的输出功率;Cch表示输出矩阵;C维单位行向量;Ach表示状态矩阵。
(19)
(20)
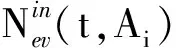
3.4 等待与放电负荷预测模型
如果不考虑电池自放电,则等待状态的EV没有充放电功率,预测模型可以表示为:
(21)
式中:上标id表示等待状态;xid(t)=[xid(t,A1),xid(t,A2),…,xid(t,AC)]T;wid(t)与xid(t)结构一致,也为C维列向量;yid(t)为t时刻闲置过程预测模型的输出功率;Aid表示闲置过程的状态矩阵。
放电过程模型如下:
(22)
(23)
(24)
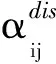
(25)
式中:Pdis表示放电功率;ηdis表示放电效率;Bs为电池实际容量。
4 算例仿真
4.1 参数设置
以某区域内600辆电动出租车为例进行仿真验证,BSS为600辆出租车提供换电服务。考虑BSS 24 h的运营状况,将一天分为96个时段,15 min为一个时段。BSS电池参数设置如表1所示。设BSS共有200组电池,运营的初始时刻为00:00,一天中初始时刻有100组电池处于可更换状态,其余电池电量在20%~80%间随机分布,电池的充放电行为可近似看作相同[35]。

表1 参数设置Table 1 Parameter setting
在Matlab软件中建立自适应FCM聚类模型,将初始时刻电池SOC数据输入至所建模型,将数据进行聚类,聚类结果如图4所示。可见,聚类数为5,按电池容量从小至大可解释为电池容量很少、电池容量少、电池容量正常、电池容量多、电池容量很多;模糊加权数为2;阈值为1×10-6。FCM的聚类结果如图5所示,可见,由于人为确定聚类数C的主观性,20%至70%的数据点间隙较大。
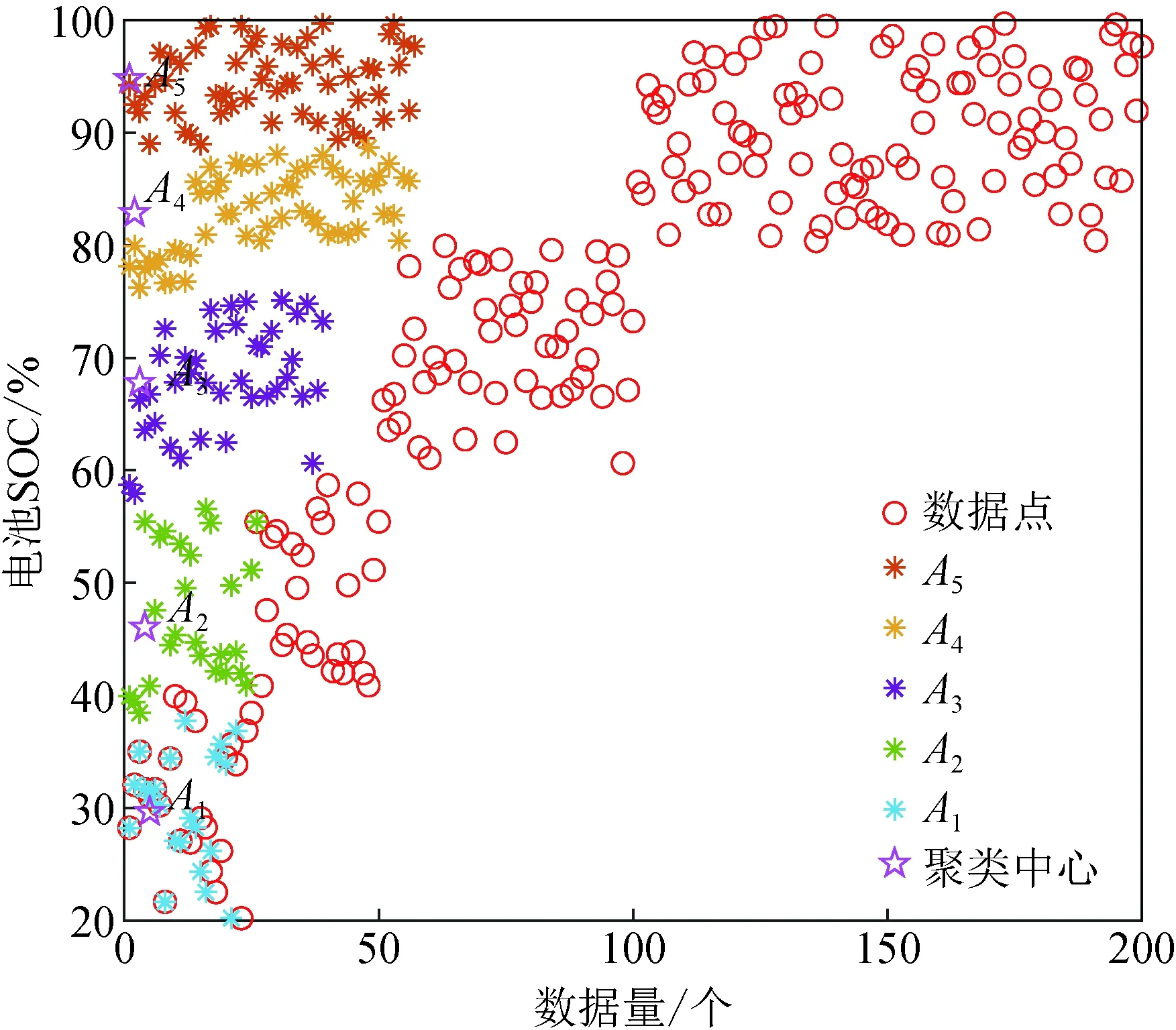
图4 自适应FCM聚类图Fig.4 Adaptive FCM clustering map
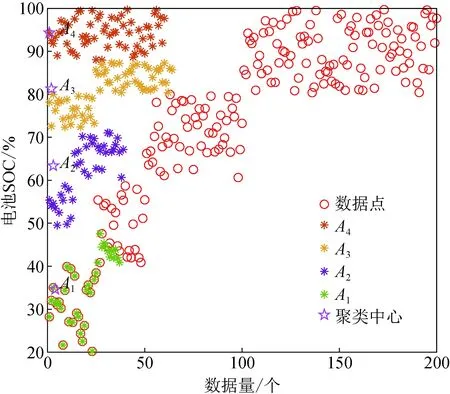
图5 FCM聚类图Fig.5 FCM clustering map
4.2 用户换电需求分析
假设EV用户在电量小于20%时会发生换电行为。此时,更换后的电池进入BSS充电,BSS换出电量大于80%的电池到EV。通过泊松分布预测各时段换电需求车辆,并与基于出行链预测方法及长短期记忆(long short-term memory, LSTM)网络预测方法进行了对比,结果如图6所示。可知00:00—06:00时段车辆较为稀少;07:00—09:00时段为上班早高峰,换电数量明显增多;10:00—17:00换电数量趋于平缓;18:00—20:00为下班高峰期,换电数量相较早高峰有显著提升;21:00—23:00换电数量明显减少,且与基于出行链预测及LSTM网络预测结果趋势保持了一致。
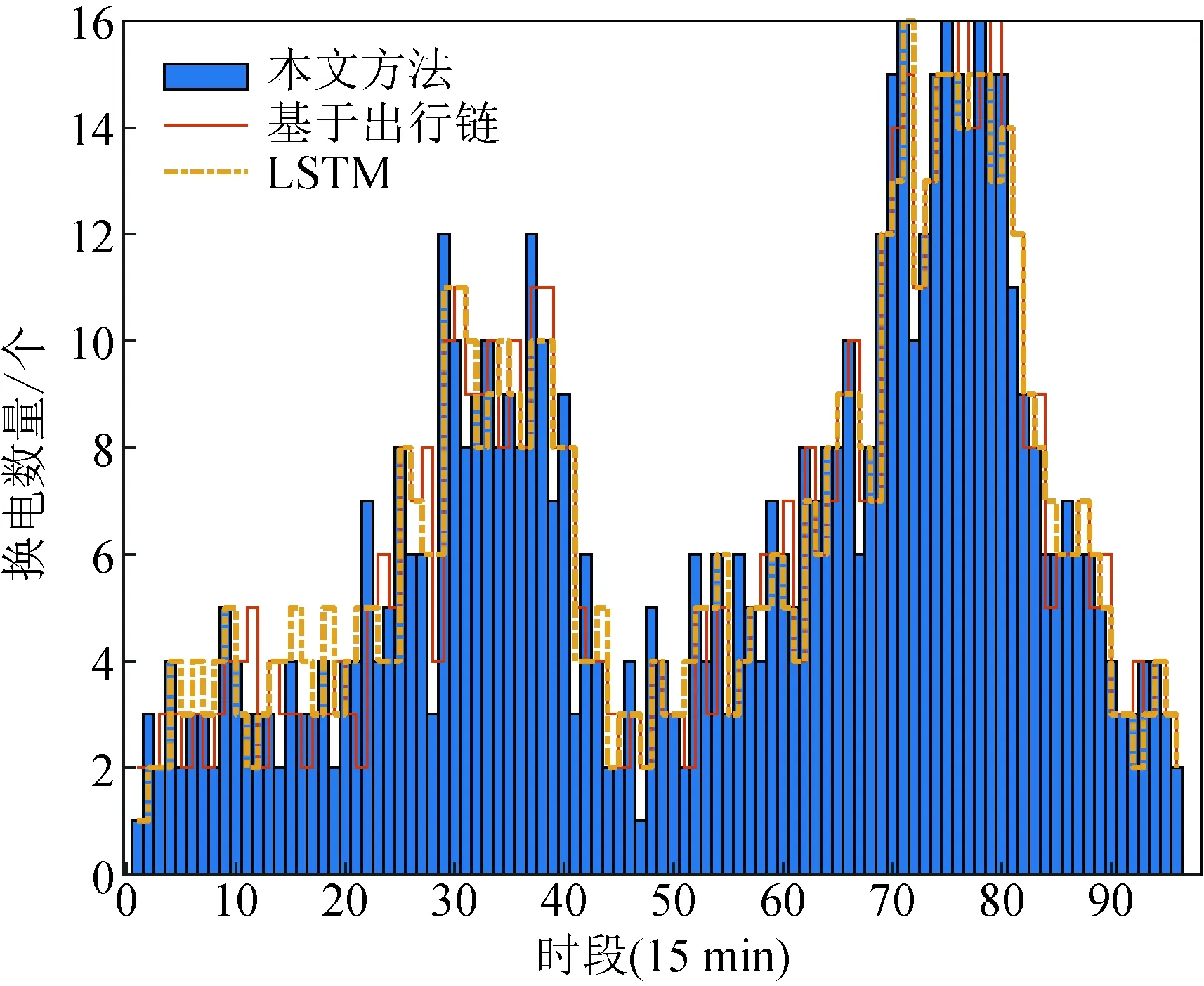
图6 换电车辆预测数量比较Fig.6 Comparison of prediction number of switching vehicles
4.3 预测模型结果及对比分析
基于模糊聚类-马尔可夫链的预测模型获取BSS各时段充电功率与放电功率如图7和图8所示。
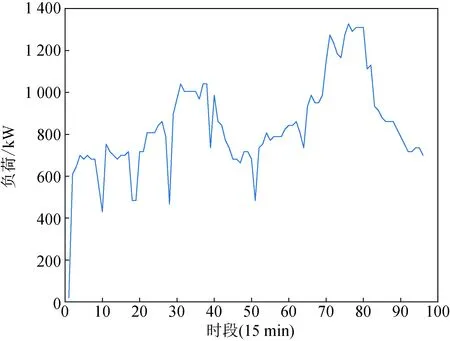
图7 聚合模型获取的BSS充电负荷Fig.7 Charge load of BSS obtained by aggregation model
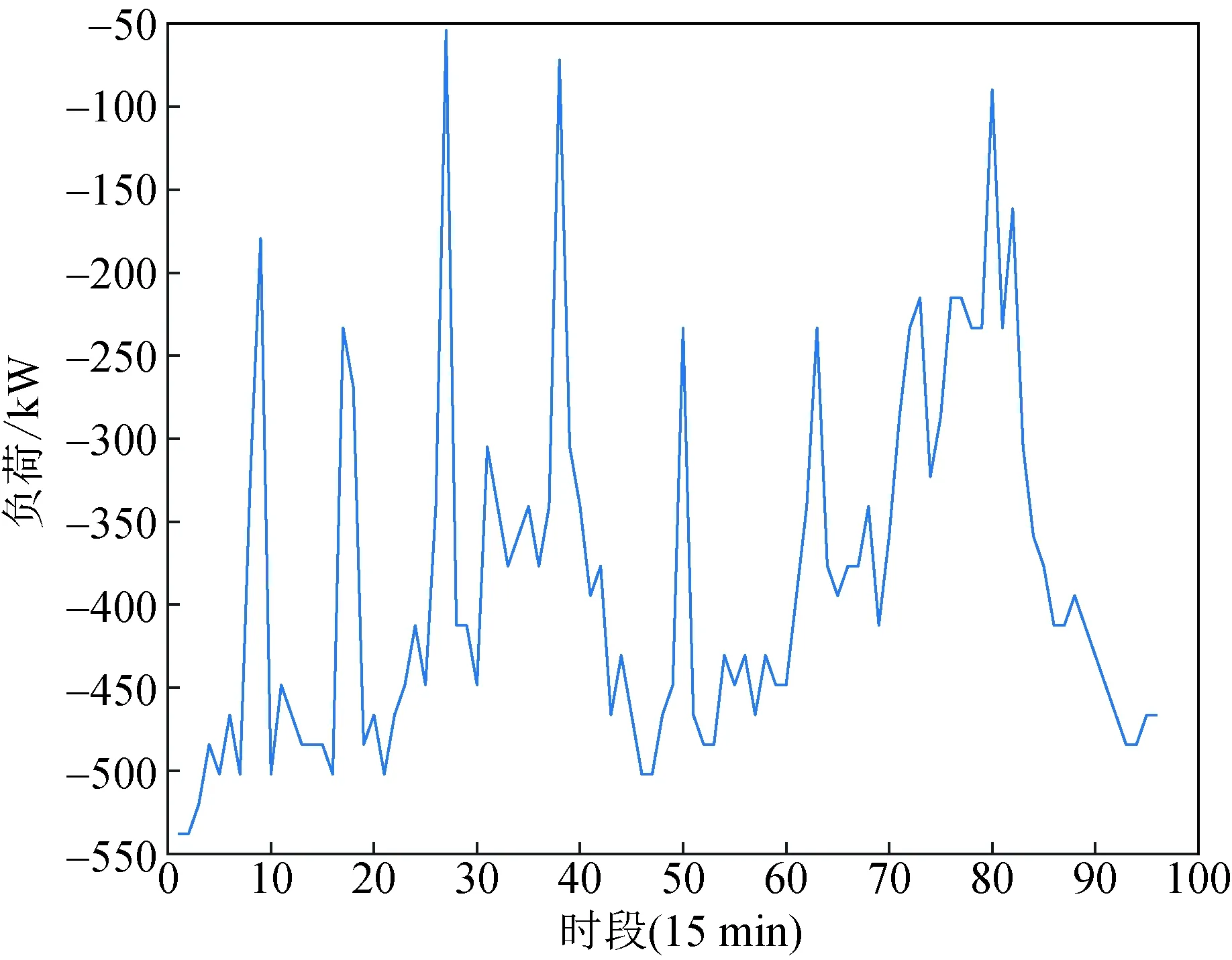
图8 聚合模型获取的BSS放电负荷Fig.8 Discharge load of BSS obtained by aggregation model
由图7可知,BSS在00:00—06:00时段充电功率为500~800 kW;07:00—09:00早高峰期间充电功率达1 000 kW;10:00—17:00充电功率为500~1 000 kW;18:00—20:00充电功率为1 200~1 400 kW;在19:00左右达到峰值1 352 kW;21:00—23:00充电功率急剧下降。由图8可知,BSS在00:00—06:00放电功率为200~500 kW;初始时刻为峰值;07:00—09:00早高峰期间因换电数量增加故放电功率减少;10:00—17:00放电功率为200~500 kW;18:00—20:00放电功率急剧减少;21:00—23:00放电功率逐渐增加至峰值。BSS放电功率在初始时刻达到峰值,而在换电高峰期放电功率则较小。
为分析所建电池负荷聚合模型的准确性,将其与蒙特卡洛模拟的聚合功率进行仿真对比。仿真参数设置与4.1节相同,蒙特卡洛模拟电池起始荷电状态符合正态分布。两种方法的对比仿真结果如图9至11所示。可知,在早晚高峰期间蒙特卡洛模拟所求充电功率波动较大,其余时间段功率波动也较频繁。比较了不同电池组规模下两种方法的BSS总负荷预测结果,如图12所示。在300组及500组电池规模下,蒙特卡洛模拟在00:00—04:00以及晚高峰期间波动较大。
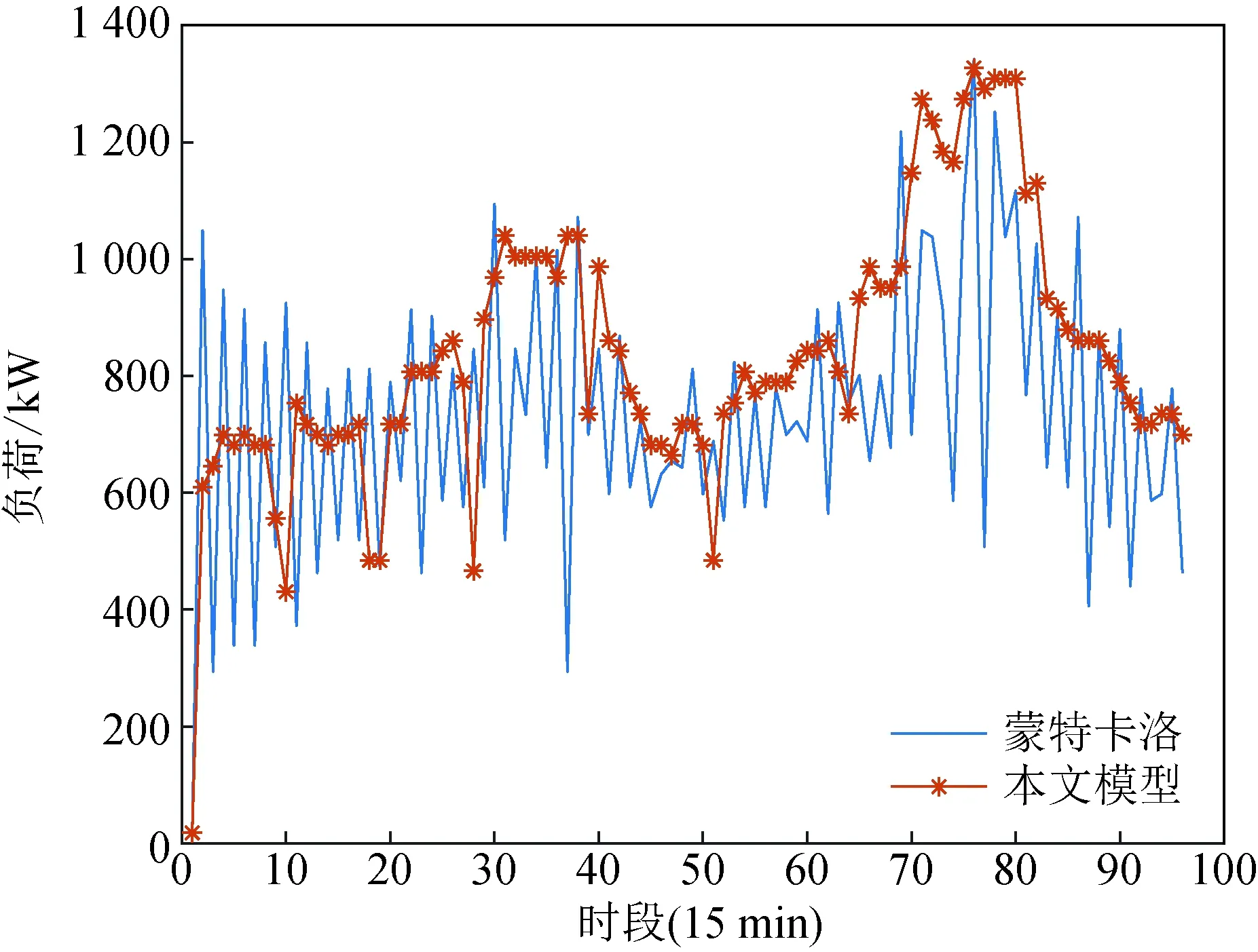
图9 充电负荷比较Fig.9 Charging load comparison
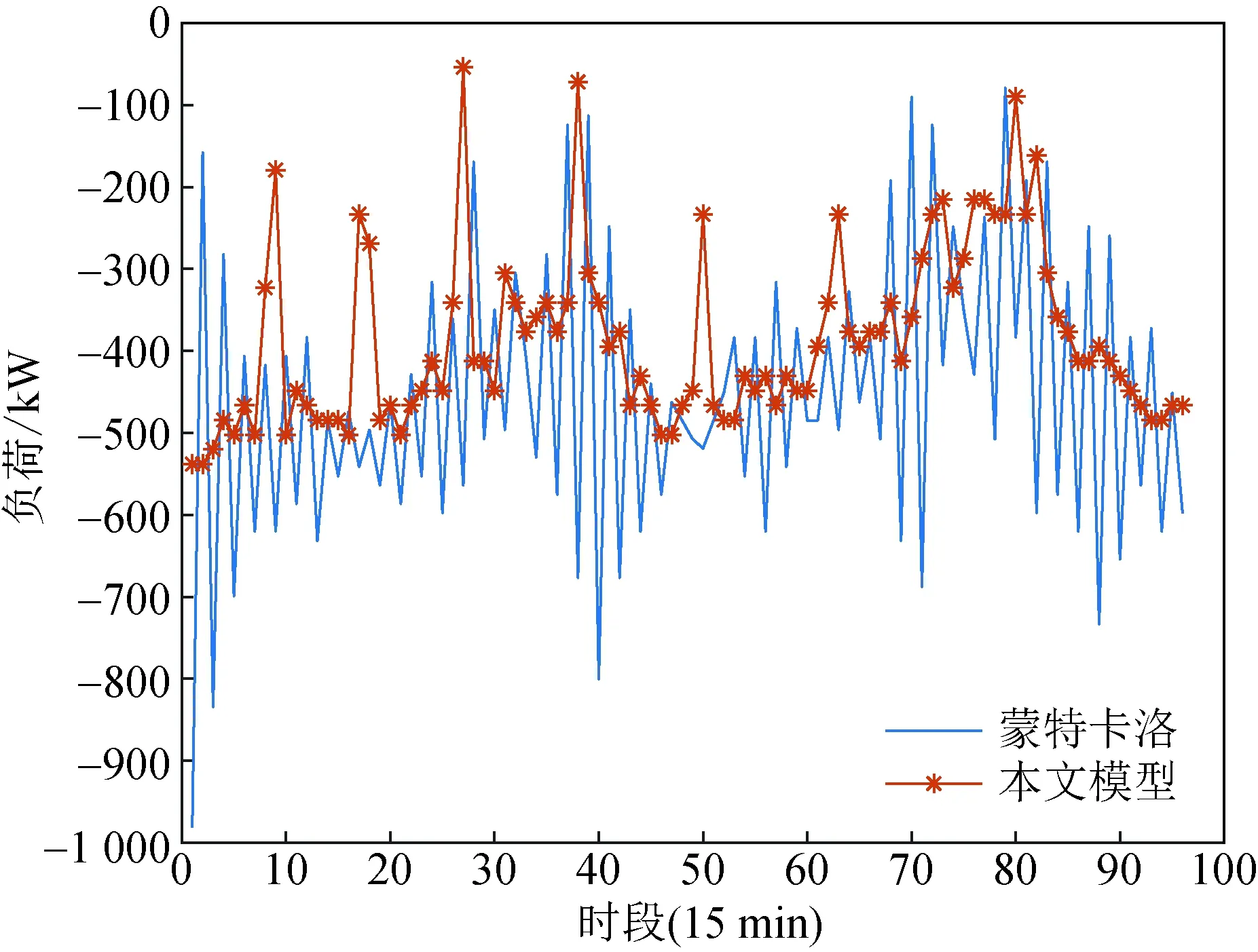
图10 放电负荷比较Fig.10 Discharge load comparison
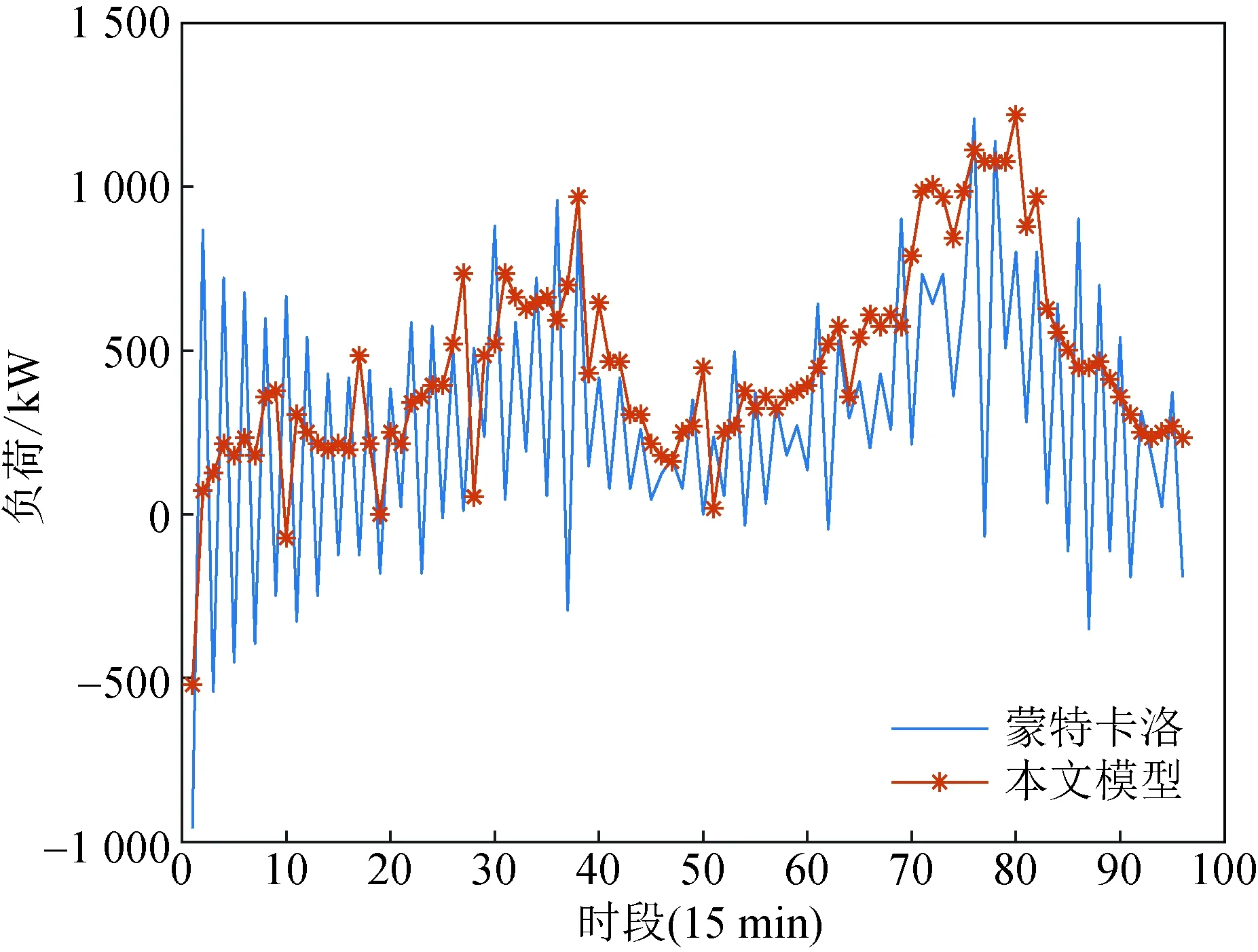
图11 一天中BSS总负荷比较Fig.11 Comparison of the total load of the switching stations during the day
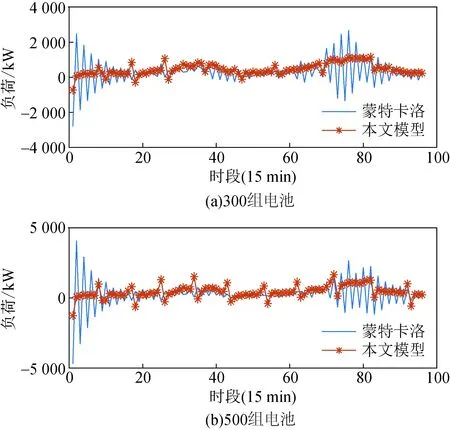
图12 不同规模电池组总负荷比较Fig.12 Comparison of battery pack loads of different sizes
可见,在整个仿真时间内,基于模糊聚类-马尔可夫链的BSS负荷预测模型与蒙特卡洛模拟法得到的聚合功率趋势保持了一致且减少了预测波动,两种方法下BSS充电负荷、放电负荷、总负荷的标准差见表2。本文模型相比蒙特卡洛预测结果的标准差分别降低了27.4%、37.7%、24.6%。说明本文构建的预测模型能够更加准确地描述BSS电池的充放电负荷动态变化过程。
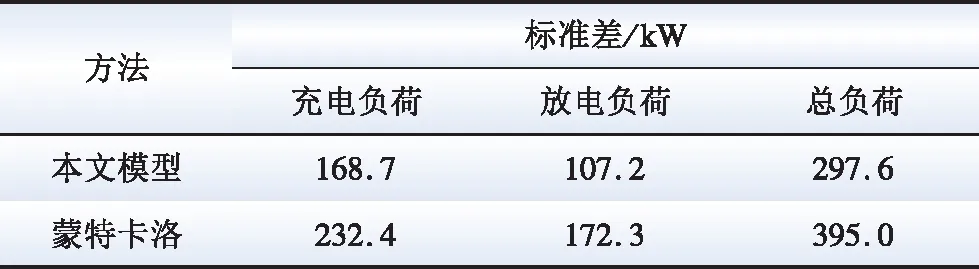
表2 标准差比较Table 2 Standard deviation comparison
5 结 论
本文在利用泊松分布预测各时刻电动汽车换电需求数量的基础上,进一步提出了基于模糊聚类-马尔可夫链的电动汽车换电站负荷预测方法,获取了充放电状态下换电站电池负荷功率。主要结论如下:
1)设计了泊松分布预测各时刻的换电需求数量,并对可供更换电池的数量进行了约束,预测结果与基于出行链及LSTM网络预测结果趋势保持一致,误差低于3%。
2)利用自适应模糊C均值聚类算法依据荷电状态对换电站中电池集群进行自适应分区,在分区基础上利用马尔可夫链建立预测模型。仿真结果表明,所建模型降低了计算难度,准确度较高,且负荷波动低于蒙特卡洛方法。
本文所建模型未考虑换电站中的电池寿命损耗问题,后续可针对此方面加以改进完善。
