基于附加阻尼控制的PMSG适应柔直送出策略优化
2023-09-27栗锐遥王潇贾辛遥田颢璟
栗锐遥,王潇,贾辛遥,田颢璟
(1. 国网北京城区供电公司, 北京市 100032;2. 国网冀北电力科学研究院,北京市 100045;3. 国网数字科技控股有限公司,北京市 100073;4. 华北电力大学电力工程系,河北省保定市,071003)
0 引 言
我国的一次能源生产、消费全球领先,其中作为能源主体的煤炭在2020年占据一次能源生产的70%以上、一次能源消费的50%以上[1],根据预测截至2025年,风电装机容量将超过5亿kW[2]。届时全球能源结构也将随着可持续发展的脚步从化石能源到可再生能源不断深化[3]。我国的风电资源主要集中“三北”地区,由于输送通道有限,导致了过去十年“三北”地区存在较大弃风率[4],传统的输电模式稳定性有限,送出的功率也有限,且需要交流同步电网作为支撑[5]。对于远距离输电,柔性直流输电的输电容量高,相对于传统输电方式成本更低,应用柔性直流技术可以大大提高电能质量,增强电网运行稳定性,且可靠性高于交流输电[6-9],但柔性直流输电与新能源发电之间的耦合关系复杂,稳定控制难度较大,主要表现:1)同步发电机特性弱、系统稳定支撑的能力差;2)柔直与风电、光伏等新发电单元的相互作用机制尚不完全明确,存在振荡风险[10]。2009年10月,美国德州南部某一双馈风电场发生次同步振荡,因系统振幅过高而导致风电机组脱网及损坏[11]。2012年我国华北地区某风电场也发生了较严重的次同步振荡,造成大量风电机组脱网[12]。
风电机组控制部分设计的不合理容易导致与柔性直流输电的控制策略不适配,可能导致风电机组经由柔性直流输电送出系统出现次同步频率、超同步频率振荡现象[13]。因此风电机组经柔直送出系统的设计和优化需经过更加细致严谨的研究来保证二者适配。
从机理角度,目前研究工作中风电和柔性直流输电混联的振荡发生机制尚未完全研究透彻,其引起振荡的因素尚不明确[14-15]。从优化角度,目前学者一般将对柔直侧加以改进优化,施加在风机侧的改进优化较为少见[16-17]。
文献[18]将新能源并网振荡现象与传统振荡现象对比,归纳新能源并网振荡的振荡形态,对大比例新能源并网的振荡风险进行评估,并分析其振荡机制。文献[19]详细描述了含电力电子变流器的风机振荡现象高发的研究现状,并基于小信号稳定性分析其振荡原因,研究结果表明,变流器与串联补偿器之间的互作用为振荡现象的主要引发因素。文献[20]表示国内某双馈风电场经某多电平柔性直流输电项目送出时出现次同步振荡故障,引发柔性直流输电停运事故。文献[21]在分析风电机组经柔性直流输电进行远距离输送的问题中,将柔性直流输电与风电机组的阻抗比作为开环传递函数,基于Nyquist判据来判断稳定性,从而探究引起该混联系统振荡的因素。文献[22]基于小信号分析法建立系统阻抗,采取扰动注入法[23-25]测得风电机组阻抗及交流侧阻抗,最后基于奈奎斯特判据对系统稳定性进行分析。
本文基于以上背景,对某直驱永磁同步风机(permanent magnet synchronous generator,PMSG)风电集群经柔性直流输电送出系统进行阻抗提取,评估其振荡风险,推导了风电机组经柔直送出系统的Bode稳定判据,最后提出用于提升该混联系统稳定性的附加阻尼控制器设计路线及控制器参数整定优化方法,最后从频域角度分析优化效果,并从时域角度仿真验证该优化效果。
1 PMSG及柔直系统建模
PMSG主要包括:风力机、永磁同步发电机、机侧变流器及网侧变流器等。直驱永磁同步风机结构示意图见图1。
1.1 PMSG模型
直驱永磁同步风力发电机的特性包含高阶、非线性、强耦合、多变量,PMSG的电磁转矩Te和有功功率Ps和无功功率Qs为:
(1)
式中:ψsd为定子d轴磁链;ψsq为定子q轴磁链;Usd为定子d轴电压;Usq为定子q轴电压;Isd为定子d轴电流;Isq为定子q轴电流;pn为发电机极对数。
1.2 变流器模型
PMSG与电网相连一般通过两电平脉宽调制(pulse width modulation,PWM)换流器,PMSG变流器由机侧变流器、网侧变流器、直流母线电容组成。背靠背换流器结构示意图如图2所示。
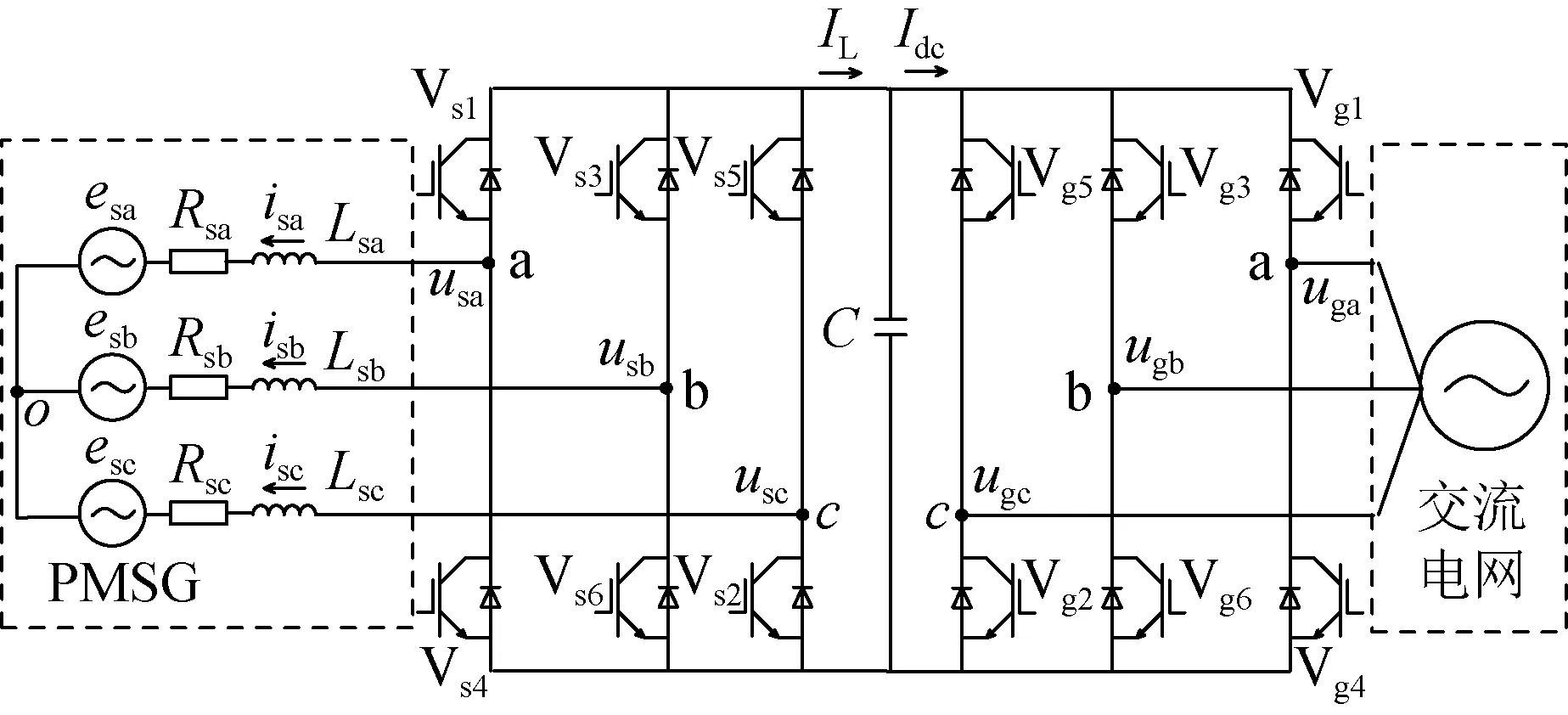
图2 背靠背换流器结构示意图Fig.2 Schematic diagram of Back-To-Back converter structure
1.3 柔直换流站模型
文献[26]建立了模块化多电平换流器(modular multilevel converter,MMC)电气系统平均值模型,用受控电压源串联受控电阻来等效桥臂电路,MMC详细模型中的六个桥臂采取受控电压源进行等效,从而实现简化模型的目的,该方法大大提升了仿真速度。
图3所示的是MMC换流器的电气系统平均值模型。
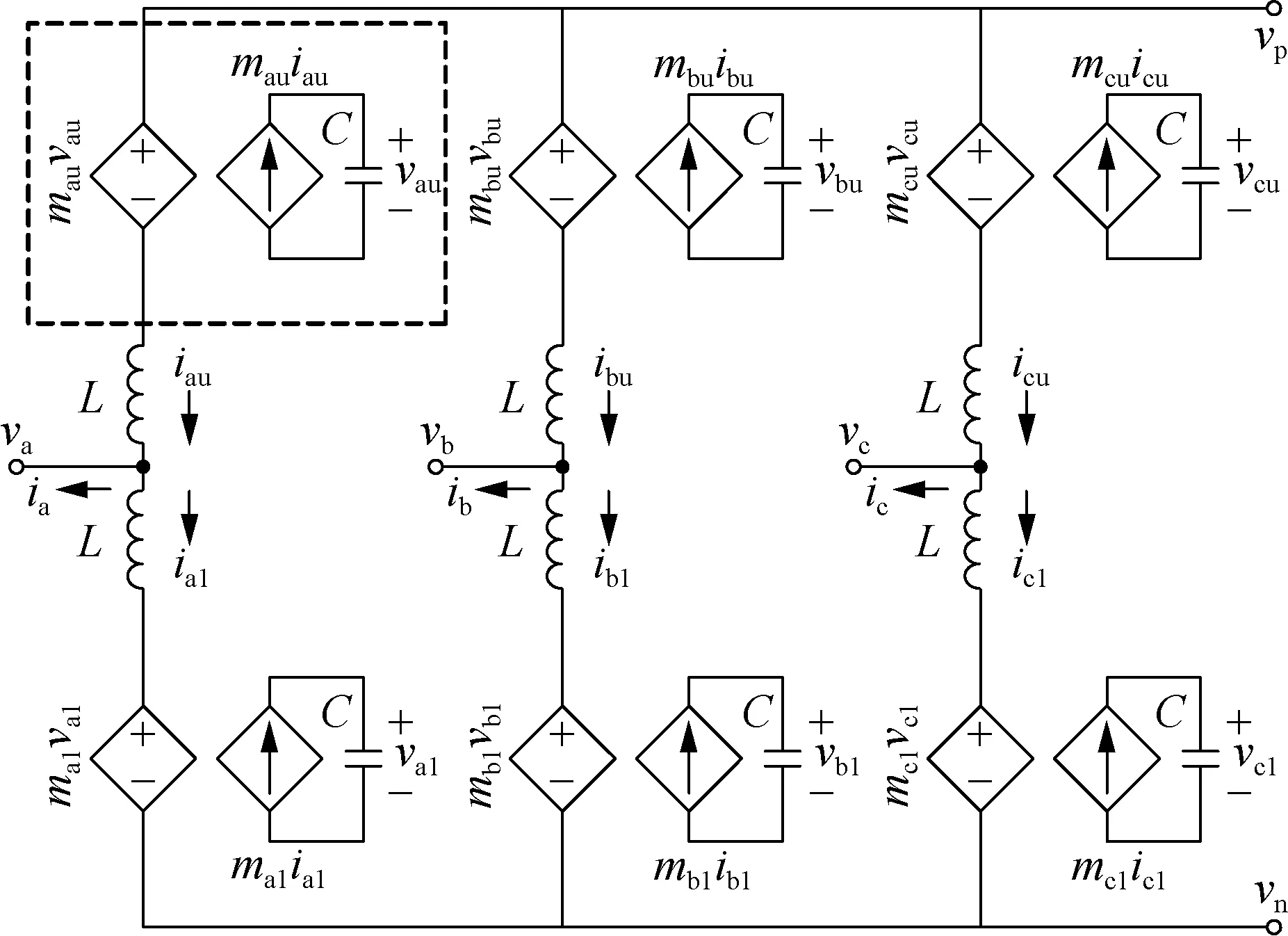
图3 MMC电气系统平均值模型Fig.3 MMC electrical system average value model
2 PMSG经柔直送出的稳定性分析
2.1 PMSG经柔直送出的Bode稳定判据
基于Nyquist判据进行如下推导。图4所示的是PMSG经柔直送出系统等效电路。以中间交互点为界,划分为“PMSG侧”与“柔直侧”两个子系统,其中“柔直侧”为柔直整个系统,PMSG侧采用诺顿等效电路替换,柔直侧采用戴维南等效电路替换。其中Iw为PMSG等效电流源,Zw为PMSG等效输出阻抗,Ug为柔直等效电压源,Zg为柔直等效输入阻抗。
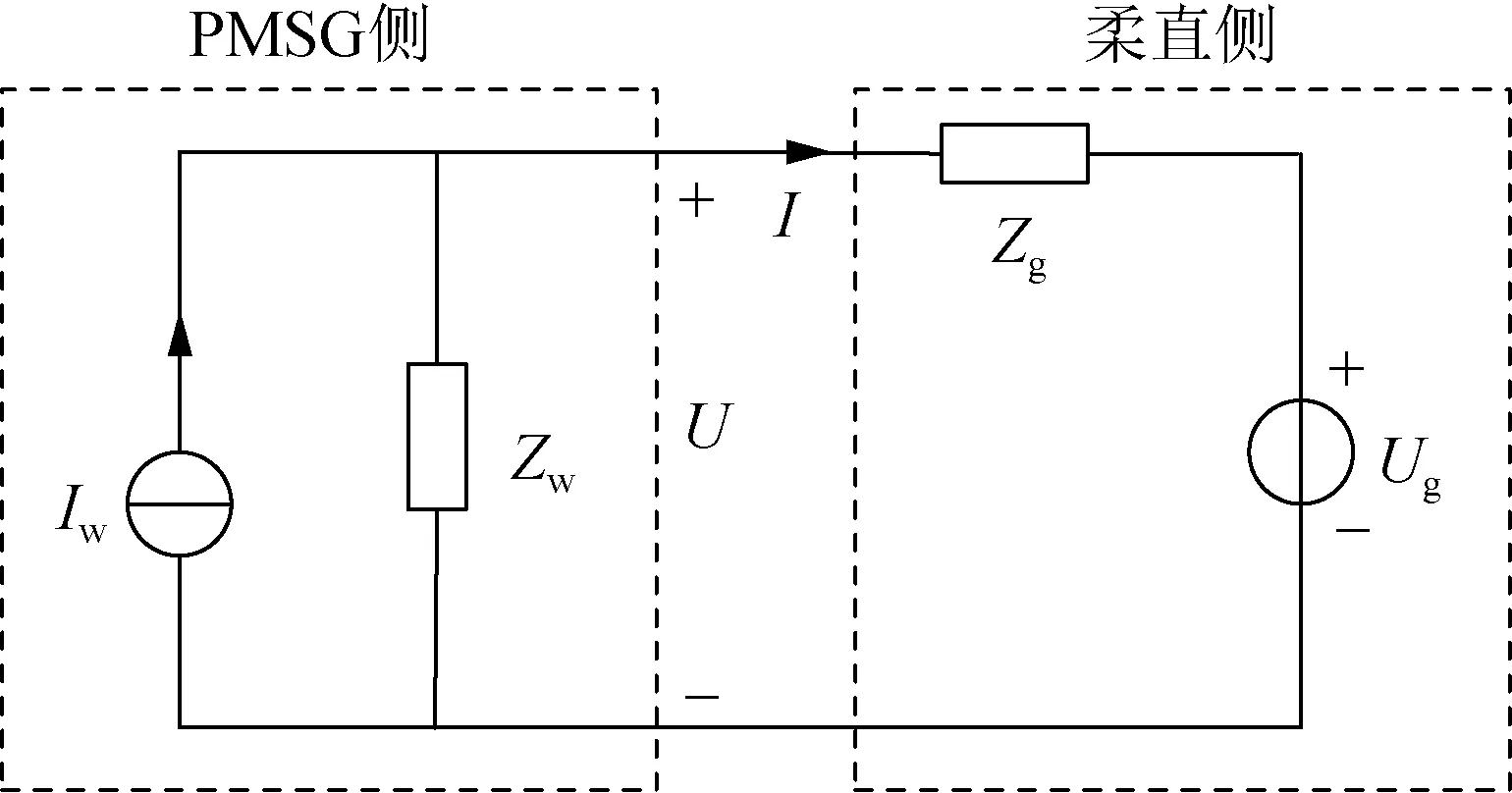
图4 PMSG经柔直送出系统等效电路图Fig.4 Equivalent circuit diagram of the hybrid system with PMSG and flexible DC transmission system
列写PMSG与柔直交互点处的电流传递函数:
(2)
交互点电流稳定的必要条件是电流传递函数的各部分各自稳定,即各部分传递函数都不含右半平面极点,则至少需满足:1)Zw(s)和Iw(s)稳定,即PMSG接入理想电压源时,PMSG自身稳定;2)Ug(s)和Zg(s)稳定,即PMSG未接入柔直,柔直本身稳定。
上述各部分稳定,则PMSG经柔直送出系统的稳定性取决于该式:
(3)
PMSG经柔直送出系统稳定的充分必要条件是H(s)的所有闭环极点都在左半平面。其中H(s)的开环传递函数为Zg(s)/Zw(s)。
伯德判据表述:若开环系统稳定,则对数幅频特性曲线为正的所有频段内,相频特性曲线正穿越(2k-1)π次数等于负穿越(2k-1)π次数(k为整数),即闭环系统稳定。
令
(4)
即
|Zg(s)|>|Zw(s)|
(5)
因此PMSG经柔直送出系统的Bode稳定判据为:在PMSG和柔直各自稳定的前提下,若|Zg(s)|>|Zw(s)|的所有频段内,∠Zw(s)-∠Zg(s)正穿越(2k+1)π次数等于负穿越(2k+1)π次数(k为整数),则系统稳定。若|Zg(s)|>|Zw(s)|的所有频段内,∠Zw(s)-∠Zg(s)正穿越(2k+1)π次数不等于负穿越(2k+1)π次数(k为整数),即系统不稳定。
2.2 提取PMSG阻抗特性
采用RT-LAB仿真平台利用扫频法对PMSG进行小信号建模。在PMSG与三相电压源间施加扰动,分析扰动后的电压电流,提取其阻抗,绘制PMSG的Bode图,利用频域分析法进行稳定性分析[27]。
本文采用步长1 Hz、幅值5%的电压扰动对1~100 Hz频段进行扫描,采用步长10 Hz、幅值10%的电压扰动对100~1 000 Hz频段进行扫描。
2.3 PMSG经柔直送出系统的振荡评估
某PMSG集群投运PMSG为 2 600台,经汇集站后采用柔直进行远距离输送。根据柔直典型参数搭建模型,并采用RT-LAB仿真平台获取柔直侧的Bode图。
为加快仿真速度,对所有PMSG简化为同工况同型号机组,应用单机倍乘等值聚合法将整个风电场的同型号风机模型化简为单机模型,从而减少风电场模型复杂程度和次同步振荡计算量[28]。图5、图6分别为1~1 000 Hz和40~60 Hz的PMSG及柔直Bode图。
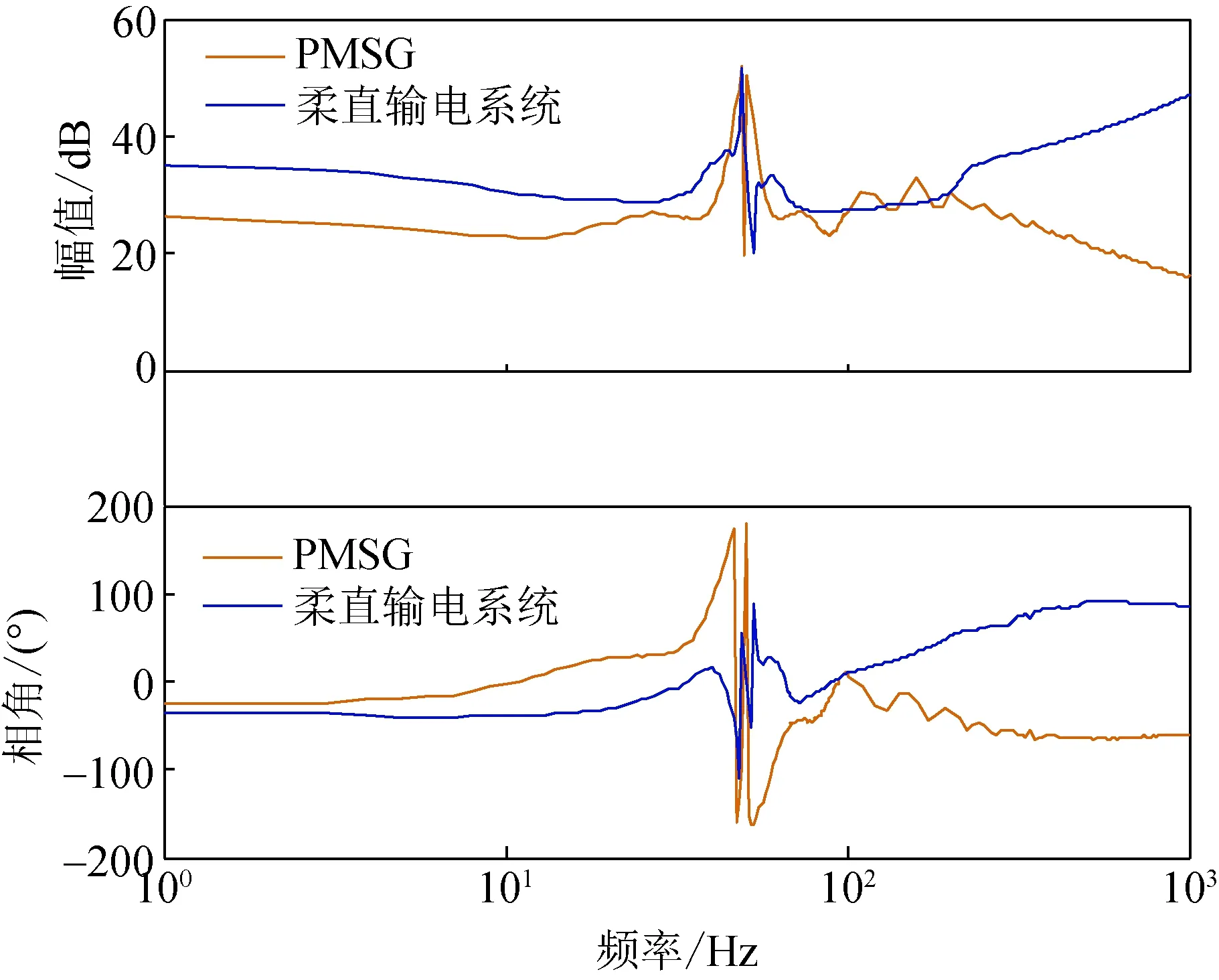
图5 1~1 000 Hz的PMSG及柔直Bode图Fig.5 Bode plot of PMSG and flexible DC transmission system for 1-1 000 Hz
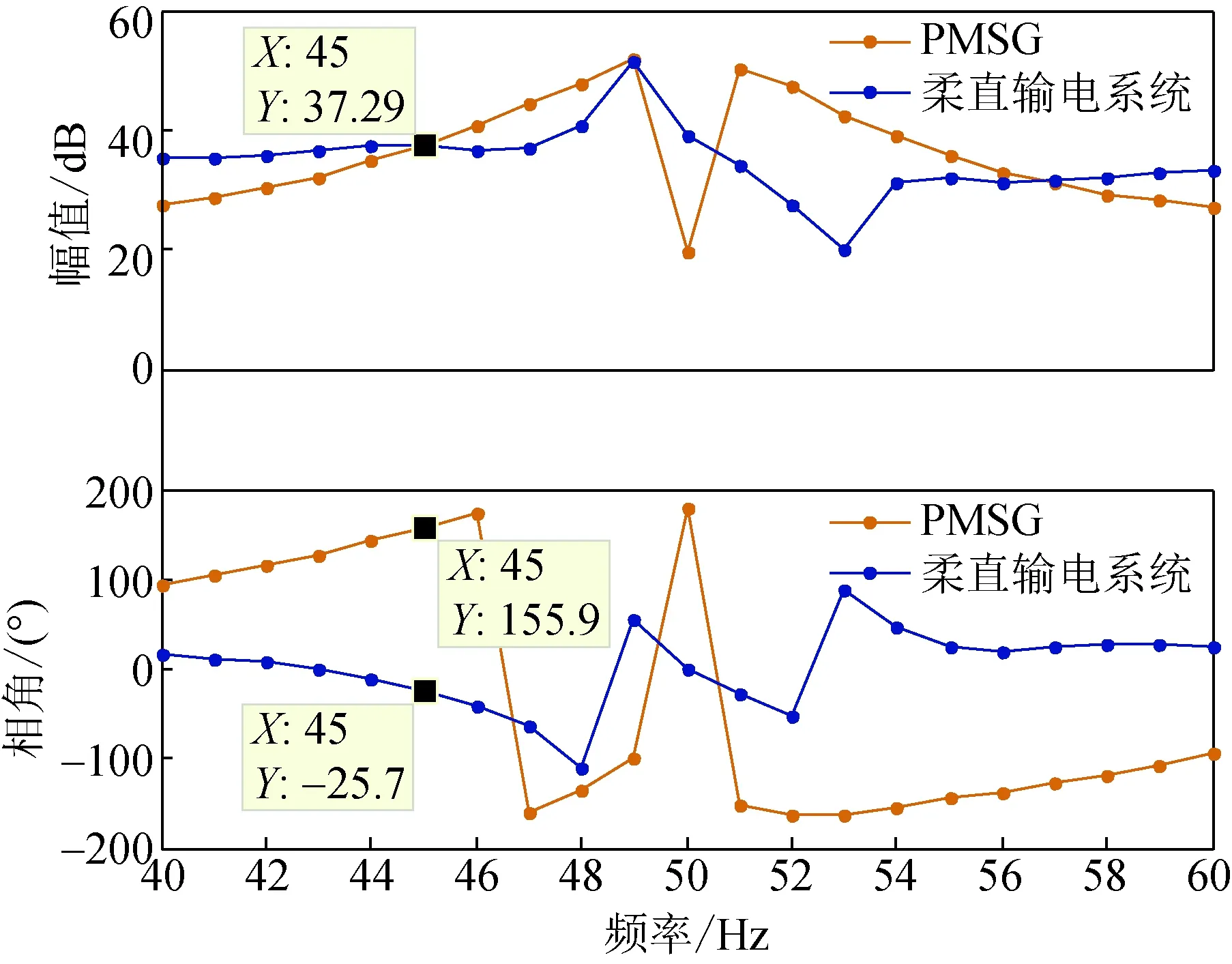
图6 40~60 Hz的PMSG及柔直Bode图Fig.6 Bode plot of PMSG and flexible DC transmission system for 40-60 Hz
通过振荡评估得到,该系统在45 Hz处PMSG和柔直存在幅值交点,交点左侧频段的PMSG幅值小于柔直幅值,45 Hz处PMSG和柔直的相角差为181.6°,45 Hz以下除邻域外的PMSG和柔直的相角差均小于180°,即在45 Hz的左邻域相角差穿越了一次180°,因此该系统存在振荡风险。经逐一检验,其他频段无振荡风险。由于幅值交点处接近180°,系统接近临界振荡状态,则振荡频率接近45 Hz。
3 PMSG经柔直送出系统振荡抑制策略
3.1 附加阻尼控制器设计方法
附加阻尼控制通过将引起振荡的信号过滤提取出来,对其进行相位超前或滞后,注入到系统中某一位置,与原有的振荡信号抵消,进而抑制振荡[29-30]。
直流电压Udc是PMSG次同步振荡现象中最为显著的影响因素。本文应用Udc作为附加阻尼控制器的信号输入。附加阻尼控制器由带通滤波器、移相器、比例增益、限幅环节组成,其中带通滤波器由高通滤波器、低通滤波器构成。图7、图8为附加阻尼控制器设计结构及其控制原理方框图。图中,Kp_out和Ki_out为外环比例增益和积分增益;Kp_in和Ki_in为内环比例增益和积分增益;Igd和Igd_ref为网侧d轴电流分量及其给定值;Igq为网侧q轴电流分量;Ugd和Ugd_ref为网侧d轴电压分量及其给定值;ωg为电网同步旋转角速度;Lf为网侧滤波电感;Udc_ref为直流电压给定值。

图7 附加阻尼控制器设计结构Fig.7 Structure of the additional damping controller
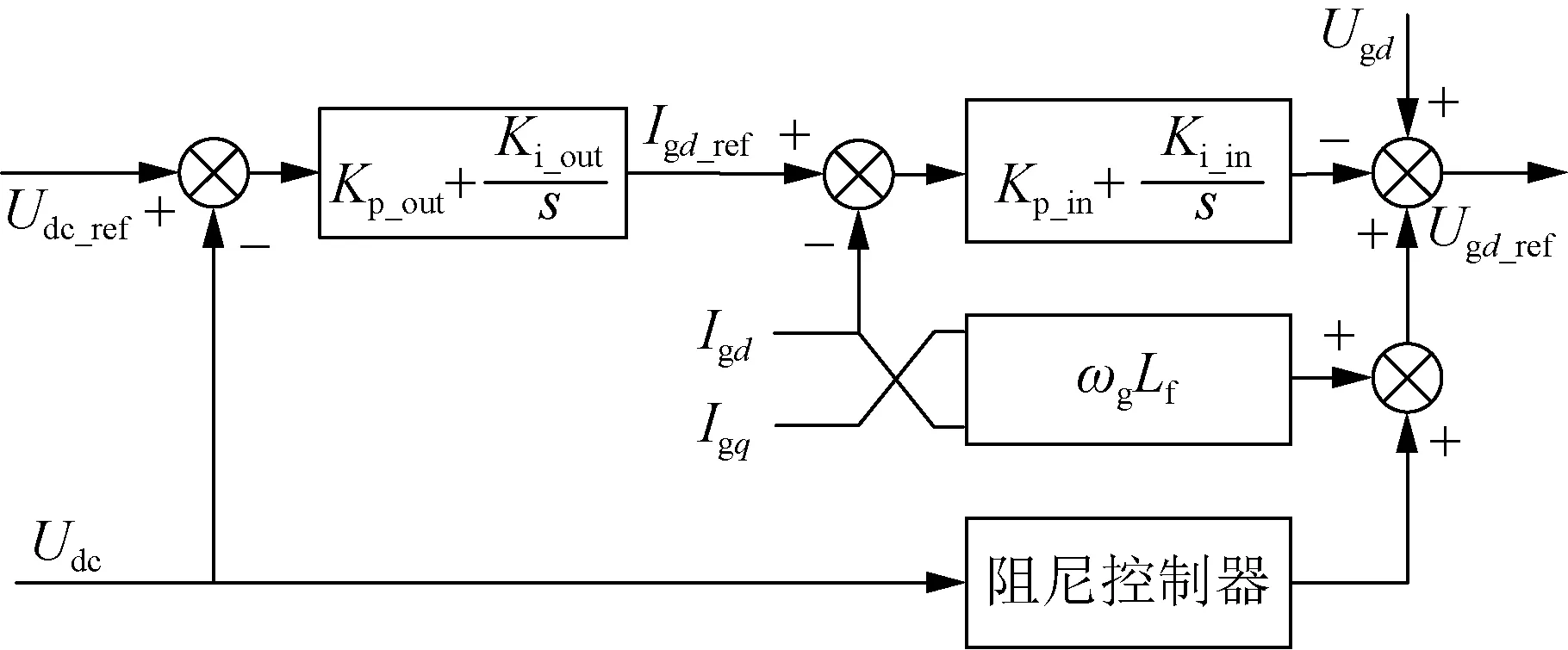
图8 附加阻尼控制原理方框图Fig.8 Control principle of additional damping controller
3.2 附加阻尼控制器参数整定
文献[31]表明,基于dq变换的频移特性,对于次同步频率的信号,在αβ坐标系下45 Hz信号经dq变换,信号频率变为5 Hz。PMSG机端三相电压的45 Hz扰动在直流电压信号中转换为5 Hz信号,因此对直流电压Udc中的5 Hz振荡信号进行抑制,即可抑制机端的45 Hz振荡。
振荡信号的提取有三大原则:1)尽可能保留振荡信号的幅值;2)使得振荡信号相位无差;3)适合的带宽范围。
经测试选定截止频率为2 Hz的高通滤波器、截止频率为12 Hz的低通滤波器。则带通滤波器传递函数Gband(s)为:
(6)
式中:Ghigh(s)、Glow(s)分别为高通滤波器传递函数和低通滤波器传递函数。
对带通滤波器进行输入输出测试,带通滤波器的Bode图如图9所示。
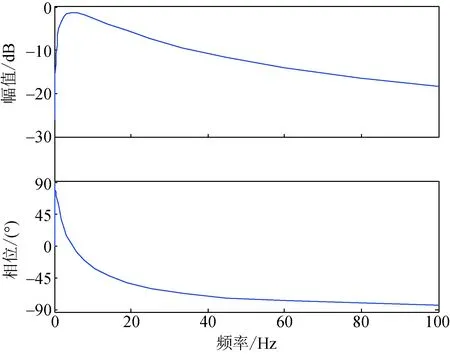
图9 带通滤波器的Bode图Fig.9 Bode plot of bandpass filter
由图9可得,带通频率为1.57~15.6 Hz,5 Hz处的幅值为-1.38 dB,大幅保留了振荡信号幅值,5 Hz处的相角为-0.388°,基本相位无差,良好地保证了目标信号的准确滤出。
设移相器为滞后网络:
(7)
(8)
(9)
式中:Gphase(s)为移相器传递函数;α>1;φm为滞后网络最大滞后角;ωm为最大滞后角的频率;T为时间常数。
由式(8)、(9)即可根据给定频率及其需要的移相角度设置移相器。
4 振荡抑制评估
4.1 频域振荡抑制评估
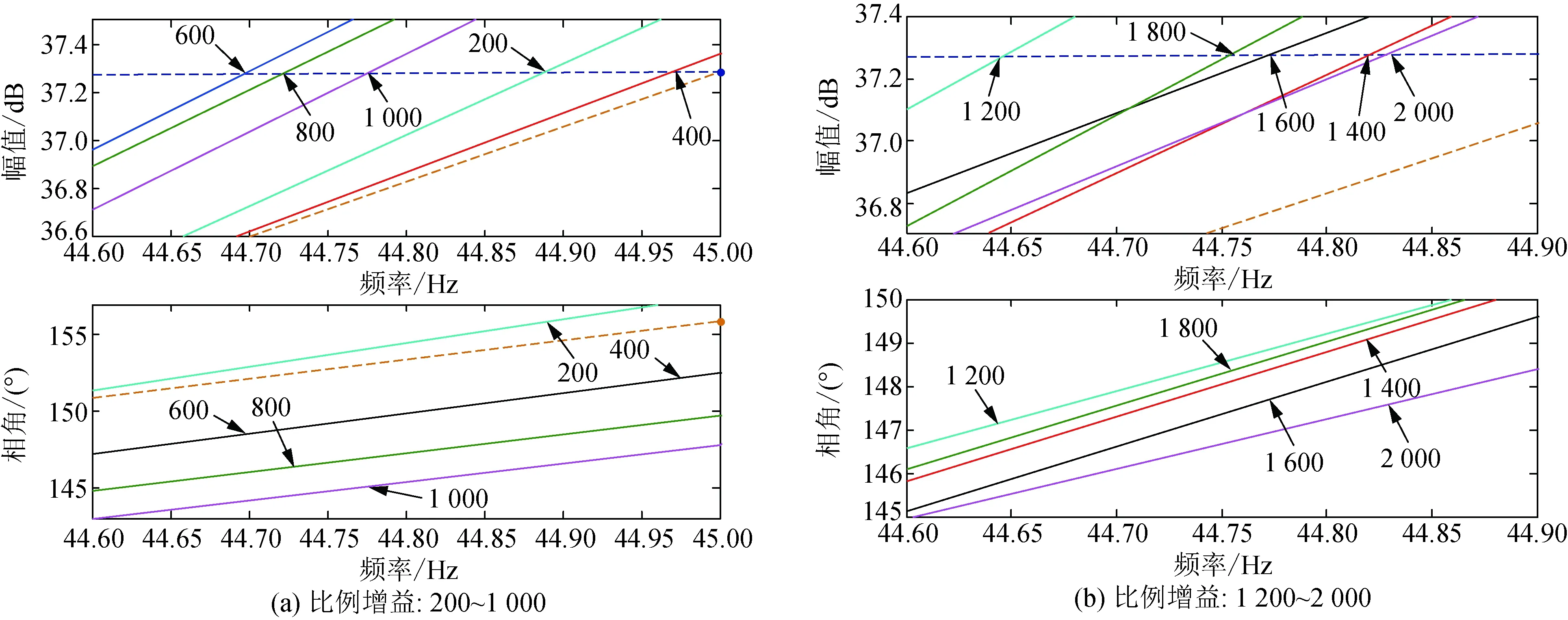
对直流电压的5 Hz频率信号分别设置了-30°、-40°、-50°、-60°、-70°、-80° 6个移相器。每个移相器均设置步长为200,200至2 000的10个比例增益,限幅器设置为±500 V/1 100 V,分别采用扫频法对单机倍乘后的PMSG进行阻抗提取。图10、图11所示的为移相-30°时比例增益分别为200~1 000和1 200~2 000的改进PMSG及柔直Bode图。移相-40°、-50°、-60°、-70°、-80°在各比例增益下改进PMSG及柔直Bode图见附录A。
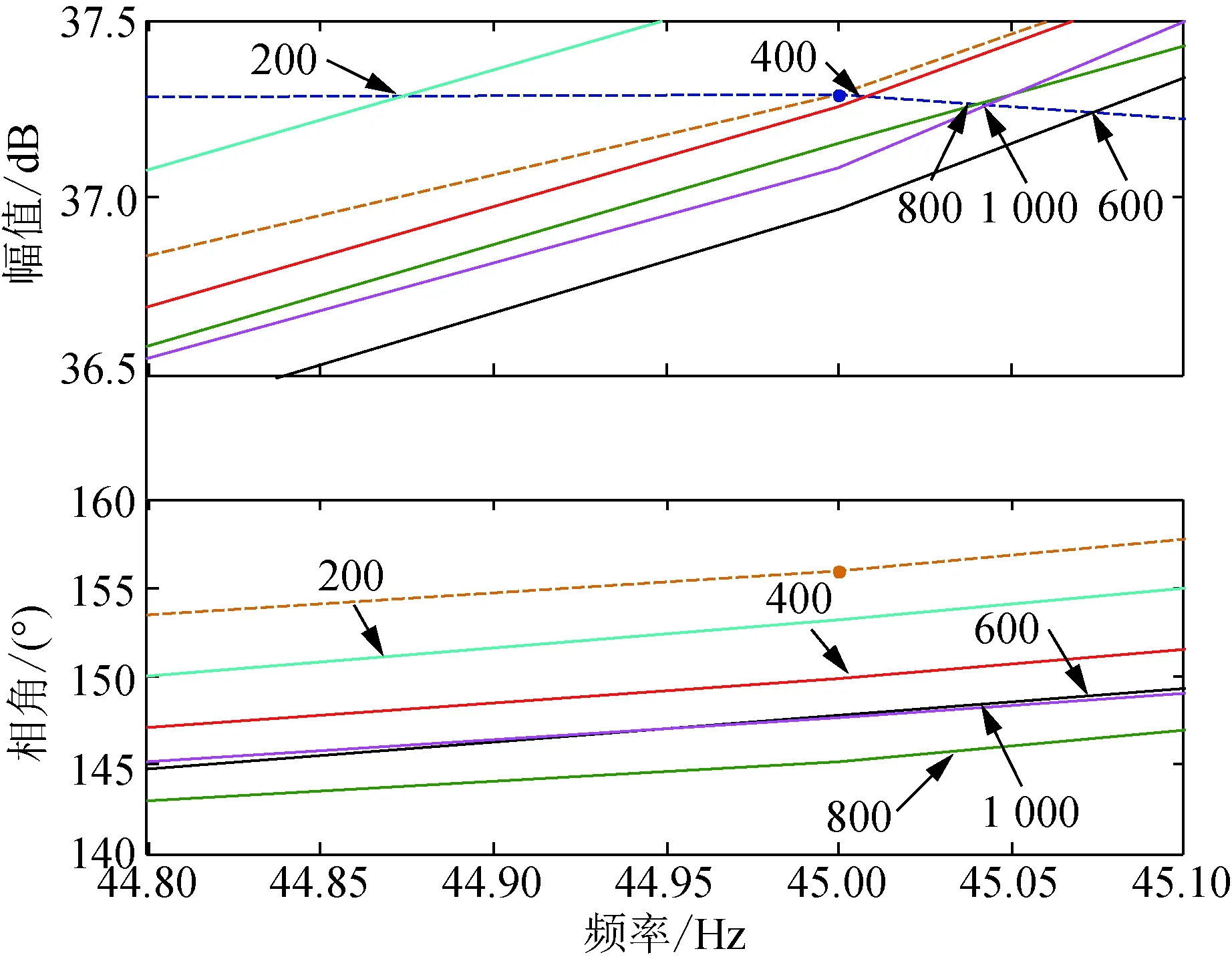
图10 移相-30°时比例增益为200~1 000的改进PMSG及柔直Bode图Fig.10 Bode plot of improved PMSG and flexible DC transmission system for -30° phase-shifts and 200-1 000 proportion-gain
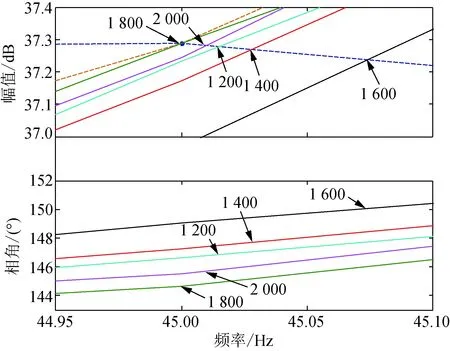
图11 移相-30°时比例增益为1 200~2 000的改进PMSG及柔直Bode图Fig.11 Bode plot of improved PMSG and flexible DC transmission system for -30° phase-shifts and 1 200-2 000 proportion-gain
箭头标记的数值为比例增益参数,幅频曲线中箭头指向的点的幅值为PMSG侧曲线与柔直侧曲线的交点幅值,相频曲线中箭头指向的点的相角为PMSG与柔直交点处频率所对应的相角。深蓝色虚线代表柔直侧的幅值、相位曲线,棕色虚线代表原始PMSG侧的幅值、相位曲线,各个颜色的实线代表附加阻尼设置为各个比例增益下的改进PMSG幅值、相位曲线。
在1~100 Hz频率范围内步长为1 Hz,所有曲线在44~45 Hz的线段和45~46 Hz的线段接近共线,该区间曲线平滑,具有较好的线性度,因此利用线性插值对44~46 Hz内的各点做线性插值,从而得到PMSG与柔直幅值交点所处频率下的PMSG、柔直相角,计算PMSG和柔直的相角差。表1为PMSG与柔直相角差。
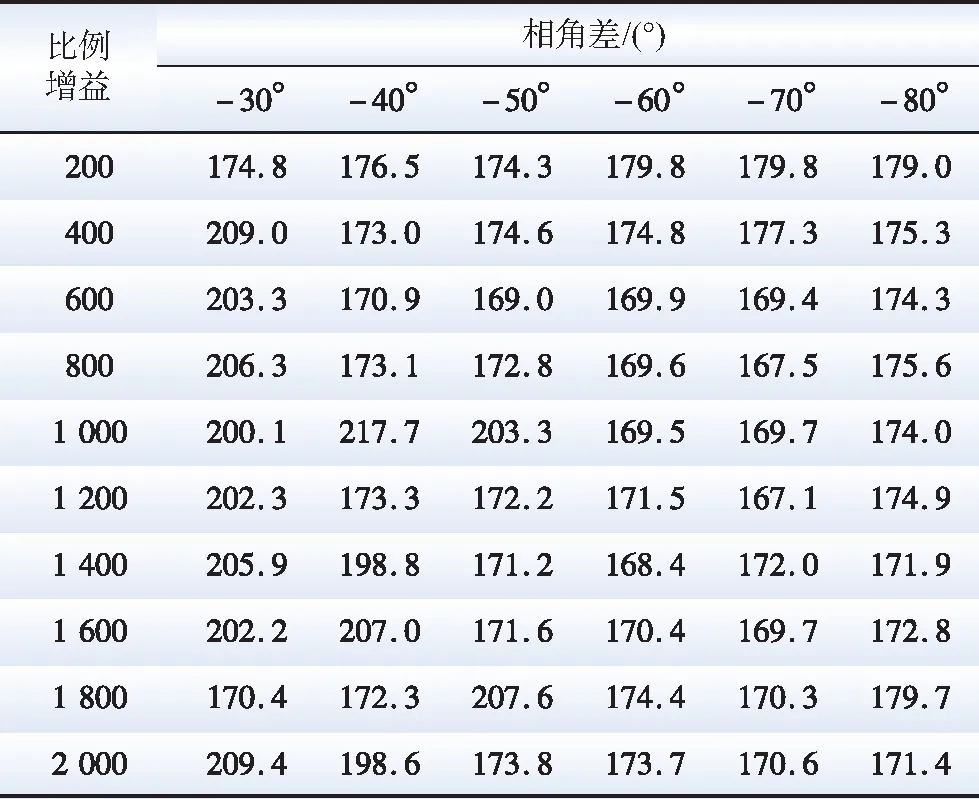
表1 PMSG与柔直相角差Table 1 Phase angle difference between PMSG and flexible DC transmission system
由表1可归纳各移相器角度及各比例增益下PMSG与柔直相角差的变化规律,定性分析得出附加阻尼控制器的整定优化方向,PMSG与柔直相角差统计图如图12所示。
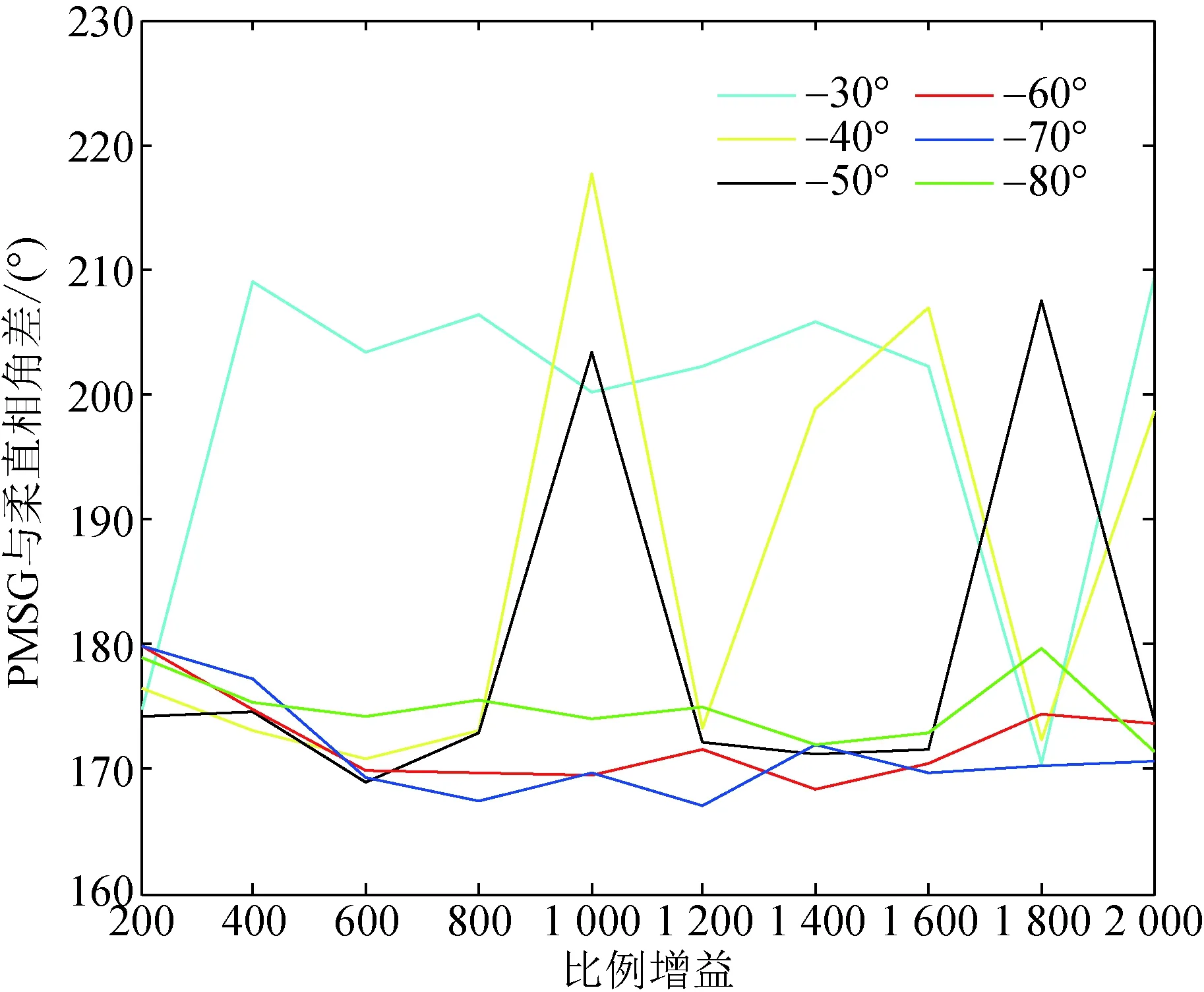
图12 PMSG与柔直相角差统计图Fig.12 Statistical chart of phase angle difference between PMSG and flexible DC transmission system
研究结果表明:1)-30°、-40°、-50°移相器只有在部分比例增益下可抑制振荡。-60°、-70°、-80°移相器在各比例增益下均能抑制振荡。2)移相器由-30°变化到-80°过程中,振荡抑制效果呈现出先增强再减弱的趋势。其中-60°、-70°的抑制效果最佳。
4.2 时域振荡抑制评估
在RT-LAB半实物仿真平台中,将PMSG与柔直模型相连,在上述频域评估中的实验数据中挑选振荡抑制效果较好的附加阻尼控制参数。将移相器设置为-60°、比例增益设置为1 400,但初始状态不投入附加阻尼控制器。PMSG起机运行后投入并如柔性直流输电,发生电压、电流振荡后,待振荡稳定,于20 s处投运设置好参数的的附加阻尼控制器。PMSG-柔直并网点相电流标幺值时域波形图如图13所示。
由图可知,PMSG-柔直并网点相电流标幺值时域波形的振幅发生波动,振幅的最小值仅为其最大值的76%,PMSG经柔直送出系统发生了次同步振荡,经FFT变换可计算得出振荡频率约为45 Hz。20 s时投入附加阻尼控制器后,PMSG-柔直并网点相电流标幺值时域波形的振幅快速趋于定值,振荡现象得到显著抑制。
对投入前的19.7 s至19.9 s的波形进行采样,经FFT分析得到45 Hz谐波含量为9.2%。对投入后的20.1~20.3 s进行采样,经FFT分析得到45 Hz谐波含量为0.7%,45 Hz谐波比例显著减少,验证了基于附加阻尼控制的PMSG经柔直送出系统振荡抑制策略的有效性。
5 结 论
本文将PMSG经柔直送出系统在并网点分为PMSG侧和柔直侧两个子系统,推导了PMSG经柔直送出系统的Bode稳定判据,提取某PMSG场站和柔直系统阻抗,并进行振荡风险评估。研究表明在45 Hz处存在振荡风险。为了解决PMSG机端特性的45 Hz次同步振荡问题,采取了抑制直流电压Udc中的5 Hz振荡信号的方案。用附加阻尼控制进行PMSG适应柔直送出策略优化,提出了附加阻尼控制器设计方法和参数整定技术。
从频域角度对改进策略的效果进行分析,在移相器由-30°变化到-80°过程中,振荡抑制效果先增强再减弱,其中-60°和-70°移相器的振荡抑制效果最好。
从时域角度进行振荡抑制评估,将PMSG与柔直相连,在上述频域评估中的实验数据中挑选振荡抑制效果较好的附加阻尼控制参数,在PMSG起机运行后接入柔直,发生振荡后投运附加阻尼控制,振荡得到有效抑制,验证了基于附加阻尼控制的PMSG经柔直送出系统振荡抑制策略的有效性。
本文推导的PMSG经柔直送出系统的Bode稳定判据及附加阻尼控制的振荡抑制方法有一定借鉴意义。但仍存在以下几个方面的问题值得进一步深入研究:
1)本文仅建模了PMSG内部的正序控制,仅采用正序扰动扫频得到正序阻抗,实际风机可能还存在负序控制,负序阻抗中也可能出现振荡风险,在后续研究中可进行完善。
2)本文针对PMSG机型进行相关控制策略优化,后续研究扩展到双馈风机、光伏发电单元等其他新能源发电机组。
附录A
图A4 移相-70°的改进PMSG及柔直Bode图Fig.A4 Bode plot of improved PMSG and flexible DC transmission system for -70° phase-shifts
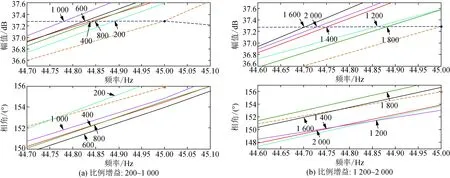
图A5 移相-80°的改进PMSG及柔直Bode图Fig.A5 Bode plot of improved PMSG and flexible DC transmission system for -80° phase-shifts
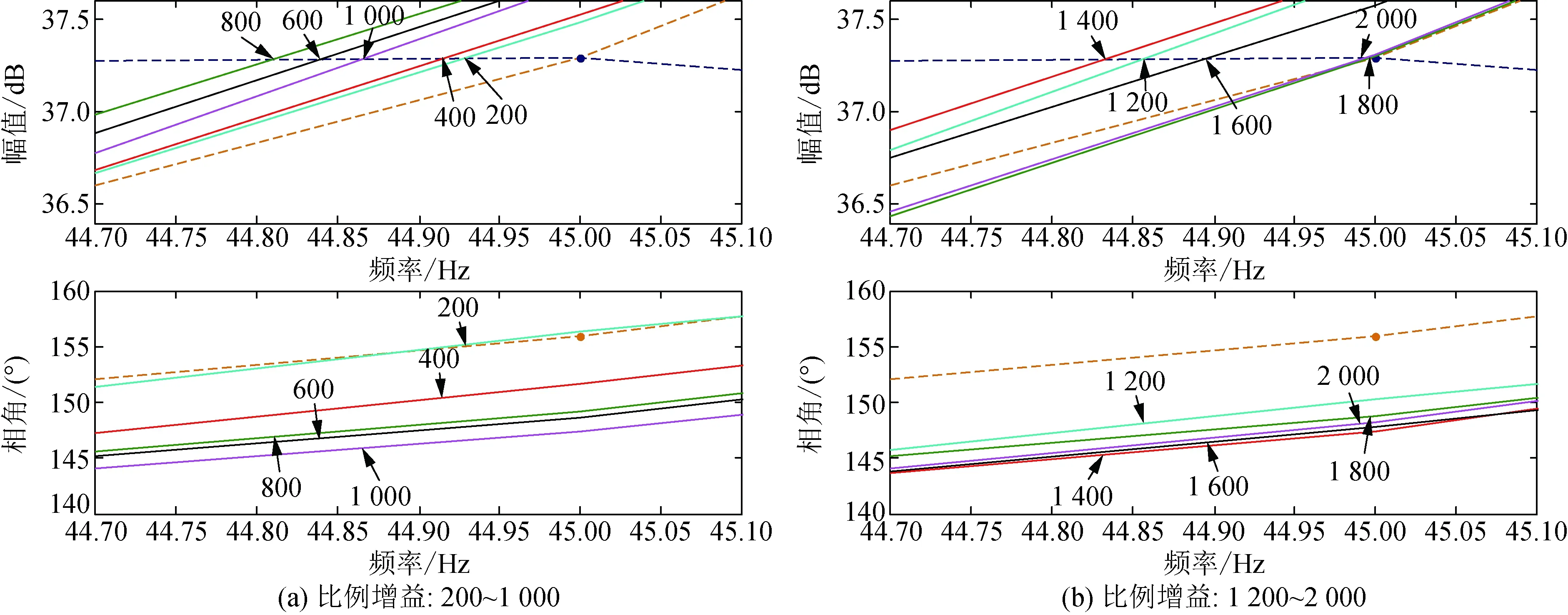
图A3 移相-60°的改进PMSG及柔直Bode图Fig.A3 Bode plot of improved PMSG and flexible DC transmission system for -60° phase-shifts
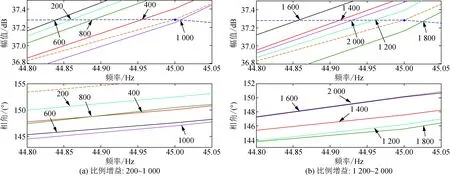
图A2 移相-50°的改进PMSG及柔直Bode图Fig.A2 Bode plot of improved PMSG and flexible DC transmission system for -50° phase-shifts
