低编译复杂度的双容错阵列码
2023-09-27王子豪蔡红亮
解 峥,王子豪,唐 聃*,张 航,蔡红亮
(1.成都信息工程大学 软件工程学院,成都 610225;2.四川省信息化应用支撑软件工程技术研究中心,成都 610225;3.中国电子科技集团第三十研究所,成都 610041)
0 引言
随着存储需求的持续增加,为保证存储系统的高性能和可靠性,独立磁盘冗余阵列(Redundant Array of Independent Disks,RAID)技术[1]得到广泛的认可和应用。由于技术发展趋势[2-3],发生并发磁盘故障的可能性随着系统规模的增长而增加[4-5],RAID-6[2]在RAID 的众多策略中脱颖而出,得到了广泛应用,并成为目前研究的重点。
RAID-6 的双容错能力通过底层的纠删码技术实现,因此,RAID-6 的性能与使用的纠删码密不可分。由于异或(Exclusive OR,XOR)运算的特性,阵列码在编译码过程中具有较低的计算复杂度,因此也常用于RAID-6 中底层纠删码的实现。典型的阵列码有EVENODD[6]、RDP(Row-Diagonal Parity)[3]和X-code[7]等。EVENODD 和RDP 使用两个特定的校验磁盘存储校验位,它们的缺点是连续的写操作会导致磁盘热点集中和I/O 瓶颈。虽然X-code 独特的结构克服了这些缺陷,但磁盘间的依赖性较强,导致扩展性不足[8]。近年来,新的阵列码也在不断被提出,如N-code[9]、EaR(Enduranceaware RAID-6)[10]以及Thou Code[11]。这些阵列码分别对复杂均衡、编译复杂度以及容错能力进行优化,可作为RAID-6的底层编码保障数据可靠性。
虽然纠删码可以容忍多个磁盘的并发故障,但在实际应用中单磁盘故障的恢复场景占全部恢复场景的99.75%[4]。因此,单磁盘故障恢复的性能对于存储系统也至关重要。但RIAD-6 中的经典阵列码EVENODD、RDP 和X-code 在单磁盘故障恢复过程中对存活磁盘的读取次数较多,单盘恢复性能不足。为了提高单磁盘故障恢复的性能,Huang 等[12]通过增加冗余位的方式,降低了单盘修复时的数据下载量;Deng等[13]对X-code 进行改进,缩小了数据重建窗口;Fu 等[14]考虑到真实存储系统中存在逻辑磁盘旋转映射到磁盘,设计了两种基于贪婪算法的恢复机制以减少修复过程I/O;Li 等[15]提出了具有双层码结构的OI-RAID,可加快磁盘恢复;Chen等[16]对HV Code(Horizontal-Vertical Code)[17]在单磁盘故障恢复上进行优化,具有更少的磁盘读取次数;Huang 等[18]改进了Liberation 码[19]的编译码算法,消除了编译码过程中的冗余计算,从而减少了数据恢复过程的异或次数。
针对现有阵列码的不足,本文提出了一种基于异或运算的混合阵列纠删码——J 码(J-code)。J-code 结合了横式阵列码和纵式阵列码的优点,具有较低的编译码复杂度和较少的XOR 操作数,还能容许任意两个磁盘的并发故障。J-code沿对角线和反对角线方向生成校验位,将部分校验位均匀分布在数据磁盘中,相较于横式阵列码中使用多个专用的校验磁盘,J-code 仅有一个校验磁盘,可以在一定程度上缓解磁盘I/O 瓶颈和失衡问题,降低了编译码复杂度;相较于纵式阵列码,J-code 提高了码率,并节省了单节点修复占用的I/O资源。
1 相关工作
在阵列码被提出前,存储系统广泛应用的纠删码为RS(Reed-Solomon)码[20],随后,Plank[21]将RS 编码算法应用于RAID 存储系统中。虽然RS 码具有最大距离可分(Maximum Distance Separable,MDS)[22]性质和理论上无限容错等优点,但它的编译码过程涉及有限域上的计算,计算复杂度高[2]。为降低计算复杂度,Blaum 等[6]提出了一种阵列纠删码EVENODD,与RS 码相比,EVENODD 最突出的优点是计算复杂度低、编译码速度快。随着研究的深入,阵列码最终取代RS 码,广泛应用于RAID 的编码实现中。RAID-6中使用的阵列码分为横式阵列码和纵式阵列码。横式阵列码的特点是原始数据位和校验位分布在不同的列上,典型的横式阵列码包括EVENODD、RDP 等;纵式阵列码的特点是校验位均匀分布在各列中,与原始数据位混合放置,典型的纵式阵列码有X-code、P-code[23]等。
横式阵列码和纵式阵列码的编码结构对它们的性能也造成了不同影响:横式阵列码有多个专用于放置校验块的校验列,校验信息集中在特定校验盘上,造成读写开销大、I/O瓶颈和I/O 不平衡等问题;纵式阵列码数据块和校验块均匀分布在各列中,具有良好的单写复杂度和编译码效率,但存储效率往往不及具有相同容错能力的横式阵列码,磁盘间紧密的逻辑联系也限制了纵式阵列码的扩展能力。
近年来,双容错的阵列码不断被提出,如EaR[10]、N-code[9]等,但学术界对混合阵列码的研究依然较少。EaR属于横式阵列码,使用两块专用的校验磁盘分别保存行校验位和对角校验位,其中保存对角校验位的磁盘比其他磁盘多存储一个数据块,因此磁盘存储的数据量并不统一。EaR 优化了编译码复杂度,但未在单磁盘恢复性能方面进行优化。N-code 是一种混合阵列码,没有专用的校验磁盘,而是将校验块与数据块一同分散在所有磁盘中,其中,行校验块按阶梯状分布,第一个磁盘和最后一个磁盘均使用一半的空间存储对角校验位。N-code 在降级读和负载均衡方面进行了优化,但编译码复杂度和单磁盘恢复性能并没有提升。目前,纵式阵列码除了X-code、P-code 外,受到的关注较少,在实际环境中的应用也很少,它们的性能和特性仍需要继续探索[24]。
综上,现有研究工作提出的双容错阵列码要么属于横式阵列码,要么属于纵式阵列码,而对混合编码方式的阵列码的研究涉及较少。因此,亟须设计混合编码模型,结合横式编码与纵式编码的优点,有效地提升双容错阵列码的性能。
2 J码
2.1 编码设计
J-code 采用混合校验规则的阵列码,与其他阵列码一样,由参数p定义,要求p必须是大于2 的素数。J-code 构造一个大小为(p-1) × (p+1)的二维阵列进行编码,不同于RDP 将校验位全部放置在两个单独的列中,也不同于X-code将校验位均匀放置在各列,J-code 采用一种折中的放置方案,即数据块分别按照斜率为-1 的反对角线和斜率为1 的对角线异或运算,得到反对角校验块和对角校验块,两种校验块分别采用横式和纵式的方式放置。全部的校验块呈“J”形排列,因此将该纠删码模型命名为J-code。J-code 编码后的二维阵列可表示为:
其中:D是由原始数据构建的(p-2) × (p+1)二维阵列;Ph是由D编码得到的1 ×p二维阵列;Pv是由D和Ph编码计算得到的(p-1) × 1 二维阵列,包括Pv1和Pv2。编码计算公式如下:
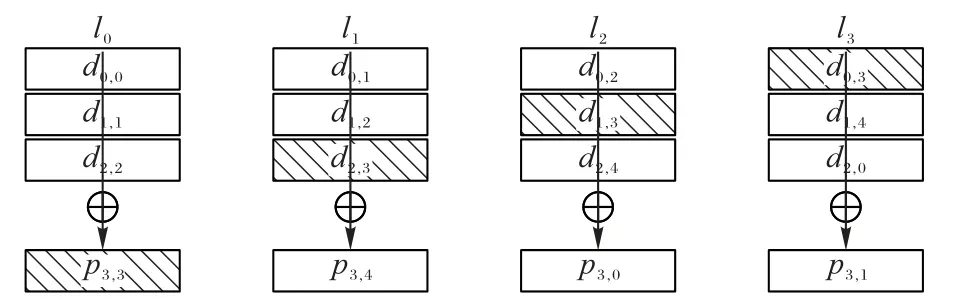
其中:di,j表示J-code 二维阵列C(p) 第i行j列的元素(i∈[0,p-2],j∈[0,p])分别表示(j+k+2) modp和(i-k) modp。本文只存储了p-1 条对角线的校验结果,同时选取pp-2,1所在的对角线作为“缺失的对角线”(missing diagonal)[6],不再进行对角校验计算。J-code 的编码过程如图1 所示。

图1 J-code的生成过程Fig.1 Process of J-code generation
2.2 译码过程
本文构造一个磁盘数为p+1 的磁盘阵列,并按0~p编号,p是大于2 的素数。定义各个原始数据块和校验块,将J-code 的构造形式化。将每个由J-code 构建的二维阵列中相同位置的块分组成一个条带。对于一个二维阵列的原始数据,先按反对角线方向将每p-2 个原始数据块分组,每组进行异或求和,并将得到的反对角校验位加入该组,将这样的一个分组称为一个反对角校验集,记为ln(n∈[0,p-1])。如图1(a)所示。当p=5 时,l0由d0,0、d1,1、d2,2和p3,3组成。可定义完整的反对角校验集合P={ln|n∈[0,p-1]}。磁盘k上存储的数据di,k所属反对角校验集为(i∈[0,p-2],k∈[0,p-1])。对于一个二维阵列的原始数据位和横式排列的校验位,沿对角线方向按p-1 进行分组,每组进行异或求和,并将得到的对角校验位加入本组,将这样的一个分组称为一个对角校验集,记为如图1(b)所示,当p=5 时由d0,0、d3,2、d2,3、d1,4和p0,5组成 。同理,定义完整的对角校验集合由于磁盘k上存储的数据di,k(i∈[0,p-2],k∈[0,p]),当i+k=p-1 时,di,k位于“缺失的对角线”上,不进行对角检验计算,即不属于任何对角校验集。di,k所属的对角校验集为:
因此,前p个磁盘中存储了反对角校验块,第p+1 块磁盘,即磁盘p中存储对角校验块,称为对角校验磁盘。
定理1 J-code 中原始数据块所属的反对角校验集与对角校验集,除当前数据块本身外没有重叠数据块。
证明 按照编码过程和参数p构造J-code,设二维阵列中存在原始数据块dx,y(0 ≤x≤p-3,0 ≤y≤p-1)。根据编码构造过程可知,数据块dx,y所属的构造反对角校验位的反对角校验集l和构造对角校验位的对角校验集l′分别为:
假设反对角校验集l和对角校验集l′存在dx,y之外的重叠元素,记为di,j,若存在i∈[0,p-2],则:
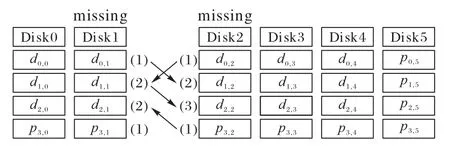
当k=0 时,i=x,对角校验集和反对角校验集在每行有且只有一个数据块,因此,数据块di,j与数据块dx,y重合,与假设矛盾;当k≠0 时,为保证i为非负整数,则必须为p的整数倍,由于0 ≤x≤p-1 当发生单磁盘数据丢失时,若故障磁盘位于前p个磁盘中,可跨磁盘0 到p-1 取出特定原始数据块和校验块构建反对角校验集进行数据恢复;若故障磁盘是磁盘p,使用前p个磁盘内的数据块和校验块即可构建对角校验集进行恢复。 当双磁盘发生数据丢失时,丢失磁盘可分为两类:一类是包含对角校验磁盘p,即前p个磁盘中的某一个磁盘与磁盘p同时发生数据丢失;另一类不包含对角校验磁盘p,即前p个磁盘中的两个磁盘同时发生数据丢失。 针对第一类情况,由于反对角校验集内数据的存储位置不涉及对角校验磁盘,因此可以仅通过反对角校验重构前p个磁盘中的丢失数据,由此,再根据对角校验集的定义便可恢复对角校验磁盘p中数据。 针对第二类情况,所有的数据丢失都发生在存储反对角校验集合的磁盘。从二维阵列结构看,对角校验磁盘p存储的校验块均属于对角校验集合P′,称对角校验集合P′与对角校验磁盘p中所有元素相交。 引理1 J-code 形式化编码构成的二维阵列前p个磁盘中任意两个磁盘未参与构造的对角校验集不相同。 证明假设丢失磁盘编号为d1和d2,d2=d1+j(j∈[1,p-1]),记两个磁盘未参与构造的对角校验集为l′n和,则: 假设m=n,则m=(n+ip) modp成立,i为自然数。由于j∈[1,p-1]且m,n∈[0,p-1],可知∀i∈N,均无法满足n+j=n+ip,于 是(n+j) modp≠(n+ip) modp,即(n+j) modp≠m与假设矛盾,假设错误,因此m≠n。证毕。 引理2 J-code 形式化编码构成的二维阵列中前p个磁盘中任意两个磁盘分别有一个与对方存储数据不相交的反对角校验集。 证明 根据J-code 形式化编码构成的二维阵列特点,前p列参与了反对角校验位的构建,因此只提取前p列,得到一个(p-1) ×p的二维阵列。第i行依次水平循环左移i个位置,得到新的二维阵列a,p=5 时对应的阵列如图2 所示。 图2 J-code的反对角校验集Fig.2 J-code anti-diagonal parity set 二维阵列a中每列元素属于同一个反对角校验集,而位于同一条斜率为1 的对角线的元素属于同一个磁盘。每个磁盘中存储的元素所属的反对角校验集构成了一个大小为(p-1) × (p-1)的阵列。如图3 所示,阴影标注的数据块存储于磁盘3,阴影数据块所属的反对角校验集构成了4 × 4的二维阵列。 图3 反对角校验集与磁盘3的对应关系Fig.3 Relationship between anti-diagonal parity set and disk3 根据结构特点易知,大小为(p-1) ×p的阵列a中必然存在一个与磁盘d中元素不相关的反对角校验集l,同时,a中元素必然分布于其他所有非对角校验磁盘中。因此,a中任选两个磁盘,则分别拥有一个与对方磁盘存储数据不相交的反对角校验集。根据a的构造原理,J-code 形式化编码构成的二维阵列同样满足。证毕。 假设前p个磁盘中两个故障磁盘分别为d1和d2,所具有的与对方存储数据不相交的对角校验集分别为lm和ln,未参与构造的对角校验集分别为。根据引理1、2 知,lm和包含磁盘d1中数据块,而不包含d2中的数据;ln和包含磁盘d2中数据块,而不包含d1中的数据。因此,首先可以通过lm、ln尝试恢复磁盘d1和d2中对应丢失的块;然后,分别探寻恢复出的数据块所属的反对角校验集和对角校验集;最后进行异或求和操作,恢复出新的丢失数据。如此循环,直至恢复全部丢失符号。当p=5 时,以磁盘1 和磁盘2 丢失为例,恢复过程如图4 所示,括号内数字与箭头分别表示恢复的次序和方向。 图4 双磁盘故障恢复过程Fig.4 Double disk failure repair process 定理2 根据J-code 的编码过程构造的二维阵列可以在其任何两个磁盘发生故障后重建。 证明 从代数的角度,可以根据式(2)、(3),构建关于丢失磁盘内存储数据的齐次线性方程组,通过证明齐次线性方程组系数矩阵任意两行满足线性无关来证明该齐次线性方程组有解,继而证出两个磁盘内数据可恢复。 假设通过参数p构建的二维阵列故障磁盘编号为d1和d2,其中,d2=d1+j,d1∈[0,p-1],j∈[1,p-1]。磁盘d1和d2存储的数据分别记为 {x0,x1,…,xp-2} 和{xp-1,xp,…,x2p-3}。由反对角校验集的构建过程,可以一般化构造方程: 其中,ci表示当前反对角校验集的其他元素的异或求和的结果。由引理2 可知,磁盘d1和d2分别存储一个特殊的元素,该元素所属的反对角校验集中没有对方磁盘中的元素,标记这两个元素分别为xm和xn,其中m=p-j-1,n=p+j-2。由式(6),根据磁盘d1和d2存储的数据所属的反对角校验集构建齐次线性方程组 由齐次线性方程组(7)构建大小为p×(2p-2)的系数矩阵的一般形式,令diag[ 1,1,…,1 ]m×m。构造的矩阵如图5所示。 根据编码构造原理及齐次线性方程组可知,系数矩阵任意两行是线性无关的,同理,根据对角校验集的构建过程,同样可以一般化构造方程: 当磁盘d1编号为0 时,即位于第一个磁盘位置,则磁盘d1中存储的元素均参与了对角校验集的构建。根据结构特点,假设磁盘d1中元素xk参与的反对角校验集不包含磁盘d2中数据块,则k=j-1,因此: 由式(9),根据磁盘d1和d2存储的数据相关的对角校验集构建齐次线性方程组: 由式(9)构建大小为(p-1) × (2p-2)的系数矩阵的一般形式,令C=diagdiag[ 1,1,…,1]k×k。构造的矩阵如图6所示。 图6 由式(9)构造的矩阵的一般形式Fig.6 General form of matrix constructed by equation(9) 当磁盘d1编号不为0 时,根据引理1,设磁盘d1和磁盘d2内数据未参与构建的对角校验集分别为,则磁盘d1中存在一个数据块属于,记为xm,磁盘d2中存在一个数据块属于,记为xn,根据阵列结构和对角校验位生成方式,有m=j-1,n=2p-2 -j,于是: 由式(8),根据磁盘d1和d2存储的数据相关的对角校验集构建齐次线性方程组 由式(10)构建大小为(p-1) × (2p-2)的系数矩阵的一般形式,令。构造的矩阵如图7 所示。根据编码构造原理及齐次线性方程组可知,无论是图6 或图7,其中任意两行都是线性无关的。根据定理1 易知,对角校验集和反对角校验集构建的次线性方程组的系数矩阵任意两行线性无关。因此,通过拼接两种系数矩阵可构建非奇异矩阵来求解未知数{x0,x1,…,x2p-3}的值,即磁盘丢失的数据。证毕。 图7 由式(10)构造的矩阵的一般形式Fig.7 General form of matrix constructed by equation(10) 对于J-code,如果故障磁盘不是对角校验盘,常规恢复方案是使用反对角校验集来恢复每一个丢失数据。例如当p=5 时,磁盘0 出现错误,可以通过反对角校验集{l0,l2,l3,l4}恢 复,其 中l0={d0,0,d1,1,d2,2,p3,3},l2、l3和l4同理。如果故障磁盘是对角校验盘,恢复方案就是使用原始数据和反对角校验位重新编码。 J-code 单磁盘故障的常规恢复方案只使用了反对角校验集,但每个数据位都受两个不同校验块的保护。本节将介绍p>3 的J-code 同时使用两个校验集的混合恢复方案,把两个校验集的重叠元素存储在内存中,以减少恢复过程中磁盘的读取次数,节省恢复时间。 观察二维阵列的前p列,由于列数比行数多1,两个校验集分别沿着斜率为1 的对角线方向和斜率为-1 的反对角线方向构造,且在每一行分别只包含一个元素。因此,任意一对反对角校验集与对角校验集至多存在一个重叠元素。 对反对角校验块的生成过程分析可知,该过程仅涉及前p个磁盘,与对角校验磁盘无关,每个反对角校验集包含p-1 个元素,其中每一个元素分布在阵列中不同且连续的列,同时位于不同行中,因此,对于每一个反对角校验集而言,存在一个非对角校验盘,它存储的数据块不属当前校验集,即存在一个不相交的非对角校验盘。同理,对对角校验块的生成过程进行分析,每一个对角校验集包含p个元素,每一个元素分布在阵列中不同行和不同列,因此,对于每一个对角校验集而言,也存在一个列与之不相交。图8 展示了p=5时校验集l0和l′0及与其不相交的列。引理3 指出了两种校验集与各自不相交的列的对应关系。 图8 两种校验集与不相交磁盘的关系Fig.8 Relationships between tow parity sets and disjoint disks 引理3 设di,j(i∈[0,p-2],j∈[0,p])为J-code 二维阵列中的一个元素,则: 1)有且仅有一个非对角校验列与其所属的反对角校验集不相交,该列编号为 2)有且仅有一个非对角校验列与其所属的对角校验集不相交,该列编号为 对于任意一个反对角校验集与对角校验集,若二者不相交的列相同,设为j。根据结构特点,若两个校验集分别按照各自斜率延伸,则会相交于dp-1,j或d-1,j,由于二维阵列只有p-1 行,因此两个数据块实际并不存在,故两个校验集不相交。 由引理3,设两个位于同一个丢失磁盘c中的元素分别为di,c和dj,c,假设di,c使用对角校验集恢复,dj,c使用反对角校验集恢复。若两个校验集不相交的列相同,则 因此,i+1+c=c-j-1+kp,其中k为整数,化简得j=kp-i-2。由于i,j∈[0,p-2],k只能取1,即j=p-i-2。由此可得出引理4。 引理4 设di,c和dj,c为J-code 二维阵列中同一个磁盘c中的两个元素,其中i,j∈[0,p-2],c∈[0,p-1],当j=p-i-2 时,di,c所属的对角校验集和dj,c所属的反对角校验集的交集为空。 证明 为减少磁盘的读取次数,应让恢复过程中用到的校验集存在尽可能多的重叠数据。由引理4 易知,当故障列中使用不同校验集进行恢复的两个元素的行编号之和不等于p-2 时,使用的两个校验集之间没有重叠数据。设丢失列中t个元素使用对角校验集恢复,剩下的p-1 -t个元素使用反对角校验集恢复,其中有k对校验集不相交,则重叠元素的个数为 存储利用率是指存储的原始数据量与全部编码信息量的比值。J-code 编码构建的二维阵列中,(p-2) ×p的阵列用于存储源数据,剩余空间存储冗余数据,存储利用率为,可容忍任意两列数据丢失。而同样能容忍两列数据丢失的EVENODD、RDP、X-code、N-code 和EaR的存储利用率对比如表1、图9 所示,其中RDP 与N-code 在同一参数p下具有相同的存储利用率。根据理论分析对比,虽然J-code 在存储利用率方面仅优于X-code,但相较于下文中J-code 降低的编译码复杂度和单磁盘故障修复I/O,J-code 所增加的存储开销仍在可接受范围内。 表1 不同纠删码的存储利用率计算公式Tab.1 Formulas for calculating storage utilization of different erasure codes 图9 不同纠删码的存储利用率对比Fig.9 Comparison of storage utilization of different erasure codes 编译码复杂度的高低是纠删码在编译码阶段的实用性和效率的体现,因此,编译码复杂度也是评价纠删码性能的重要指标之一。J-code 作为阵列码的一种,基于XOR 运算的编译码计算方式使其计算复杂度远低于基于Galois 域GF(2w)运算的纠删码,如RS 类纠删码与再生码。 下面以每种阵列码的数据位构造校验位所需的异或操作平均次数作为衡量编码复杂度的指标,对EVENODD、RDP、X-code、N-code、EaR 和J-code 进行对比。根据J-code 的编码过程可知,J-code 的每个信息位都参与了反对角校验位的构建,斜率为1 的部分对角线上的信息位与反对角校验位参与了对角校验位的构建,因此一个J-code 码字的编码过程总异或次数为 2(p2-3p+1),编码复杂度为。EVENODD、RDP、X-code、N-code 和EaR 的编码复杂度对比如表2、图10(a)所示。其中,EVENODD 的原始构建方式要求p+2 个磁盘,除了X-code 外的其他纠删码的构建都要求使用p+1 个磁盘,假设这些纠删码都应用于具有p+1 个磁盘的存储系统中,为保持统一,令EVENODD 逻辑上的最后一个数据磁盘只存储零。而RDP 与N-code 在同一参数p下具有相同的编码复杂度。 表2 不同纠删码的编码和译码复杂度计算公式Tab.2 Calculation formulas of encoding and decoding complexity of different erasure codes 图10 编码复杂度和译码复杂度对比Fig.10 Comparison of encoding complexity and decoding complexity 类似地,以每种阵列码恢复两列数据位过程中异或计算次数与原始数据块之比作为衡量译码复杂度的指标。在此,假设数据丢失都发生在存储原始信息的列中。由第二章Jcode 的译码过程可知,J-code 恢复两列丢失数据XOR 操作次数 为2p2-7p+4。因此,J-code 的译码复杂度为。EVENODD、RDP、X-code、N-code 和EaR 的译码复杂度对比如表2、图10(b)所示,其中,RDP 与N-code 在相同参数p下具有相同的译码复杂度。 如图10 所示,当p=3 时,J-code 具有最低的编码复杂度;随着p的增加,J-code 的编码复杂度仅高于X-code 并逐渐趋于一致,而J-code 的译码复杂度始终保持最低,说明J-code具有优秀的编译码性能,在理论上能提高存储系统的编译码速度。 单磁盘故障修复I/O 指修复任意一个故障磁盘时对其他磁盘的读取次数。本节仅考虑存储原始数据的磁盘丢失的情况。第3 章详细阐述了J-code 的混合恢复方案,在此不再赘述。EVENODD、RDP、X-code、N-code 和EaR 的单磁盘修复硬盘读取次数如表3、图11 所示,其中EVENODD、RDP、Xcode 同样采用单磁盘故障最优恢复方案[25]。与4.2 节一样,EVENODD 逻辑上的最后一个数据磁盘只存储零。由图11可知,随着编码参数p的增加,J-code 始终具有最少的磁盘读取次数,说明了在单磁盘故障修复过程中,J-code 占用最少的I/O 资源。 表3 不同纠删码的单磁盘故障修复硬盘读取次数计算公式Tab.3 Calculation formulas of read times for single disk failure repair of different erasure codes 图11 不同纠删码的单磁盘故障修复磁盘读取次数对比Fig.11 Comparison of read times among different erasure codes for single disk failure repair 为评估J-code 在真实应用场景下的性能,在编码用时、单磁盘故障恢复时间和双磁盘故障恢复时间方面进行了实验对比。该实验横向对比的纠删码分别是J-code、EVENODD、RDP、X-code、N-code 和EaR。编码参数p的取值为3、5 和7。与上文一致,EVENODD 逻辑上的最后一个数据磁盘只存储零。用于测试的文件的大小为5 MB,为实现各个阵列码条带数统一,设置当编码参数p=3 时,数据块分块大小设为600 KB;当p=5 时,数据块分块大小设为100 KB;当p=7 时,数据块分块大小设为50 KB。实验的软件运行环境是CentOS7 64 位操作系统,硬件环境为CPU Intel Core i5-10400、内存8 GB、机械硬盘1 TB*8。 4.4.1 编码用时实验 从表4 编码过程的用时可看出:由于J-code 在生成反对角校验位过程中,XOR 计算次数少于EVENODD、RDP、Ncode,因此编码速度得以提升。由于EaR 每个条带多存储一个校验块,导致编码时间比J-code 长。而X-code 的特殊构造方式使它具有最低的编码复杂度,从而具有最快编码速度。相较于EVENODD、RDP、N-code 和EaR,J-code 的编码时间分别减少了6.96%~28.70%、0.30%~20.20%、0.60%~23.60%、7.00%~22.80%。随着p的扩大,编码时间趋于稳定,各个阵列码的用时相差不大。 表4 不同编码参数p下的用时对比Tab.4 Comparison of time consumption under different encoding parameter p 4.4.2 单磁盘故障修复用时实验 从表4 单磁盘故障的平均修复用时可看出:当p=3 时,在单个条带内,相较于其他阵列码,J-code 采用常规恢复方案时具有最小的磁盘读取次数,因此修复速度最快。而Xcode 由于需写入数据块最多,因此耗时最长。当p>3 时,Jcode 采用混合恢复方案仍能实现最少的磁盘读取次数。综合三种编码参数,在单磁盘故障修复过程中,J-code 相较于EVENODD、RDP、X-code、N-code 和EaR,故障修复时间分别减少了7.20%~17.46%、5.40%~14.68%、10.61%~31.62%、6.81%~16.22%、2.23%~10.58%。 4.4.3 双磁盘故障修复用时实验 从表4 双磁盘故障的平均修复用时可看出:在双磁盘损坏场景下,J-code 的修复过程需要读取的数据块个数比EVENODD、RDP、N-code 和EaR 少,同时需要写入的数据块个数比X-code 少,因此J-code 的修复时间最短。实验结果表明,相较于EVENODD、RDP、X-code、N-code 和EaR,J-code 的译码时间分别减少了9.43%~29.10%、6.05%~16.23%、15.58%~36.00%、5.88%~15.67%、0.39%~12.41%。 在磁盘阵列中,由磁盘故障导致的数据丢失对企业及用户造成巨大损失。目前已有多种阵列码被用于实现RAID-6的容错机制,但编译码复杂度较高,单盘、双盘恢复速度较慢。为此,对横式阵列码与纵式阵列码进行分析,提出了一种结合二者编码特点的混合阵列码J-code,阐述了编译码过程以及单磁盘快速修复方案,并证明其正确性。通过理论分析,J-code 在满足RAID-6 双容错能力的同时,具有较低的编译码复杂度和单磁盘故障修复I/O。实验结果表明,相较于EVENODD、RDP、N-code 和EaR,J-code 能够减少编译码时间和单磁盘故障修复时间,而在存储利用率方面稍有不足;相较于X-code,J-code 优化了存储开销,节省了译码时间和单磁盘故障修复时间,而在编码时间方面稍有不足。此外,J-code的校验生成规则也在一定程度上缓解了数据修复过程中磁盘I/O 失衡的问题,因此J-code 适合用于磁盘阵列的底层编码实现,具有应用前景。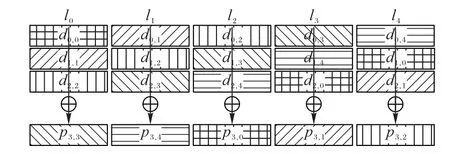

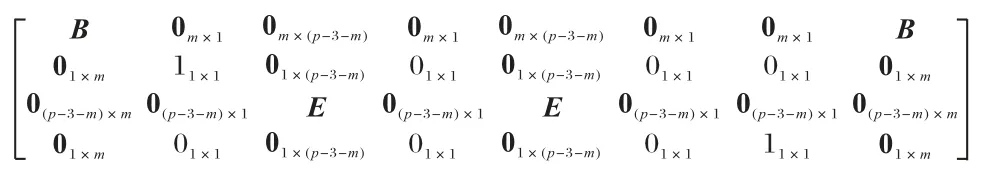
3 单磁盘故障恢复方案
3.1 常规恢复方案
3.2 混合恢复方案

4 实验与结果分析
4.1 存储利用率和容错率

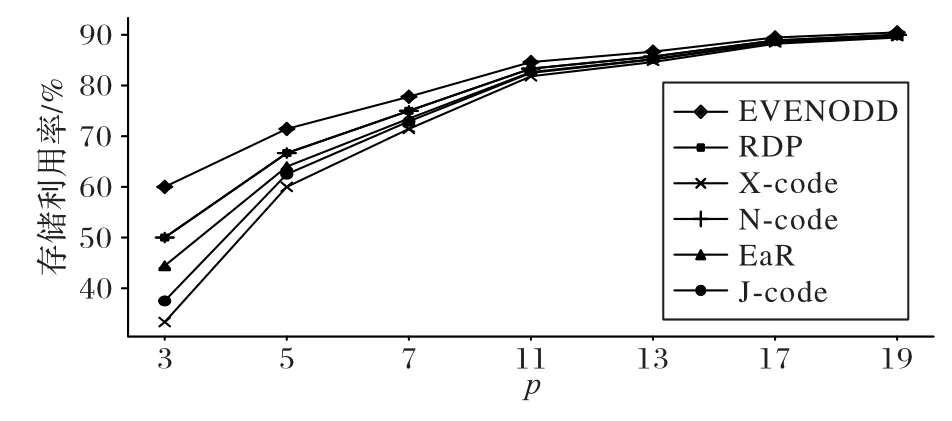
4.2 编译码复杂度

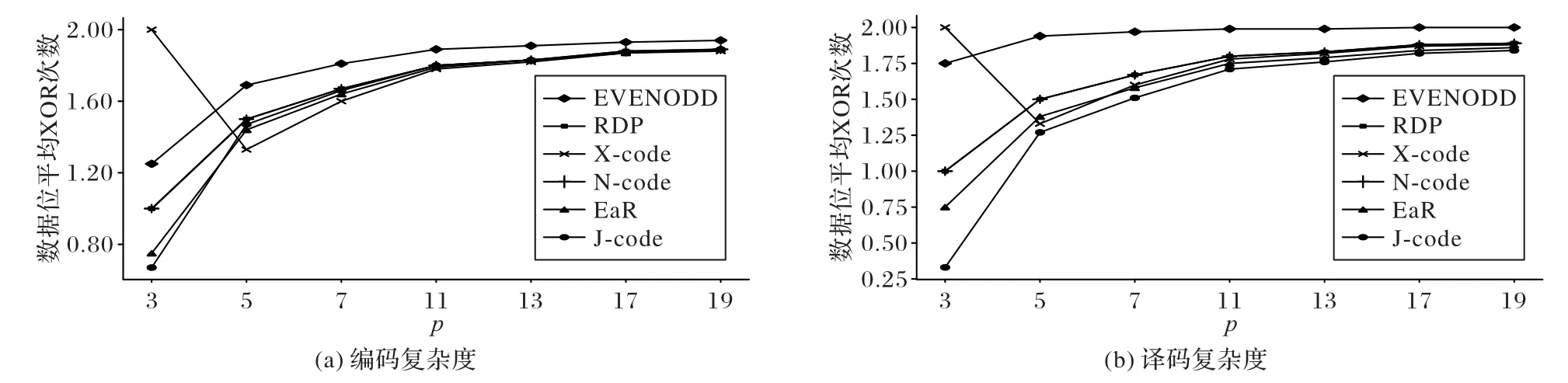
4.3 单磁盘故障修复I/O

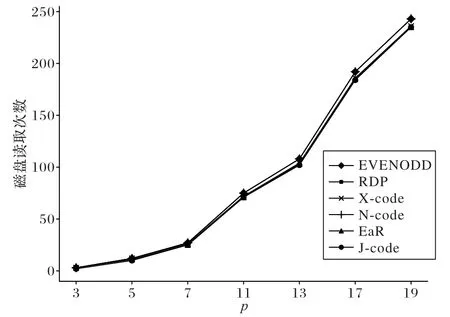
4.4 真实应用场景下的实验对比
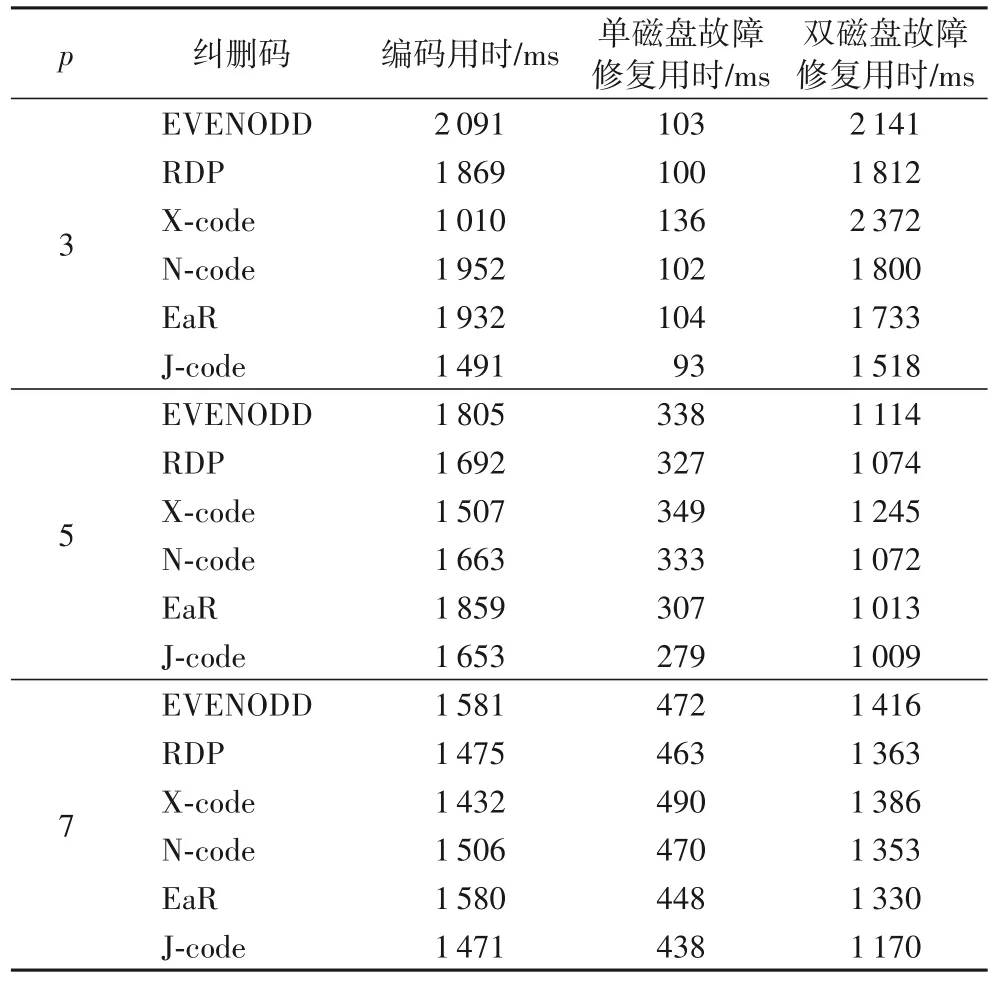
5 结语
