基于混合机制的深度神经网络压缩算法

赵旭剑，李杭霖

（西南科技大学 计算机科学与技术学院，四川 绵阳 621010）

0 引言

随着深度神经网络（Deep Neural Network，DNN）的快速发展和应用，对于深度神经网络的压缩需求也愈发强烈。如表1 所示，神经网络的计算复杂度随模型复杂度增加而增加，这为DNN 在有限资源设备的部署移植带来了困难与挑战。传统的DNN 中通常含有庞大的参数，这些参数一定程度上代表着模型复杂度，决定模型占有的空间大小，这些参数往往存在冗余［1］。因此，如何减少冗余信息并对深度神经网络模型进行压缩的研究具有重要理论意义。

表1 经典神经网络对比Tab.1 Comparison of classical neural networks

本文针对深度神经网络因模型存储空间和计算量大而难移植至嵌入式或移动设备的问题，通过深入分析已有深度神经网络压缩算法在占用内存、运行速度及压缩效果等方面的实验性能，以mini-ImageNet 数据集为基础，融合知识蒸馏、结构设计、网络剪枝和参数量化的压缩机制，基于AlexNet 建立深度神经网络压缩模型，提出一种基于混合机制的深度神经网络优化压缩算法。

本文的主要工作如下：

1）系统分析了深度神经网络压缩算法影响要素，提出了一个基于AlexNet 的影响要素分析研究框架。

2）提出了一种基于混合机制的深度神经网络压缩优化算法。采用知识蒸馏的思路设计学生网络和教师网络两个神经网络作知识迁移，使学生网络从教师网络中学习“知识”，再通过对学生网络进行结构设计和网络剪枝的操作来缩小学生网络的体量大小，并通过参数量化进一步缩小学生网络体积达到网络压缩的效果。

1 相关工作

随着深度学习的快速发展，对DNN 的计算量需求也越来越大，这无疑加速了对DNN 压缩算法的研究，于是网络剪枝、知识蒸馏、参数量化、结构设计等压缩算法相继出现。

网络剪枝［2］是为压缩深度神经网络而提出的删除权重张量中冗余参数的算法。早在20 世纪90 年代，LeCun 等［3］就提出了网络剪枝的概念，主要步骤包括预训练、剪枝和微调。网络剪枝的压缩算法有多种实现方法，Wang 等［4］提出从零开始剪枝（prune from scratch）的方法并在CIFAR10 和ImageNet 数据集上进行验证，该方法在进行网络剪枝前随机初始化权重以获得多样化的剪枝结构，甚至能够获得性能更优的模型；Dong 等［5］提出将神经网络结构搜索直接应用于具有弹性通道和层尺寸的网络，通过最小化剪枝后网络的损失来减少通道数；Chen 等［6］提出为每个卷积层引入一个显著性剪枝模块（Saliency-and-Pruning Module，SPM），SPM 需要先学习并预测显著性分数，然后将其应用剪枝到每个通道，这种自适应网络剪枝方法能够降低卷积神经网络（Convolutional Neural Network，CNN）的计算量；Wen 等［7］对剪枝权重与神经元的选择作对比分析，在准确率不受影响的条件下，得出结果为：对权重剪枝会导致剩余神经元接受不同数量的输入，利用不同GPU 进行加速的效果均不理想，稀疏剪枝实际上是令神经网络中的矩阵更稀疏，通过不同方法使某些神经元失活，但实际上内存的占用并未减少。

Hinton 等［8］首次提出知识蒸馏的概念，通过引入与教师网络相关的软目标来促进学生网络训练，达到知识迁移的目的，使学生网络能学习来自教师网络的隐藏信息。由于深度神经网络的网络层数较多，且每层含有较多网络参数，Romero 等［9］提出使用回归模块来配准部分学生网络和部分教师网络的输出特征，并对输出特征进行相应处理，将网络处理的重点放在特征层以更高效地进行知识蒸馏，知识蒸馏往往需要先预训练教师模型，再通过蒸馏将知识传递给学生模型，该训练过程会带来运行速度的减慢。

参数量化的实现方法很多，它的中心思想是令多个参数共享取值。Vanhoucke 等［10］和Hwang 等［11］通过fixed-point 降低参数精度，令取值相近的参数共享一个数值。Chen 等［12］提出利用哈希桶的方式压缩神经网络，将神经网络的权值随机划分到多个哈希桶，其中同一哈希桶内共享同一参数以实现神经网络的压缩。之后，他们在此基础上又提出一种新网络FreshNets（Frequency-sensitive hashed Nets）［13］，将网络卷积核变换到频率域并在频率域进行随机哈希，对重要性低的高频部分使用更低的哈希位数表示，以实现更高压缩。Gong等［14］通过K-means 聚类算法对参数进行聚类操作，每簇参数共享中心值以达到压缩神经网络的目的。

调整神经网络架构可以只需要比较少的参数达到压缩神经网络的目的，该类方法统称为结构设计。深度可分离卷积是其中一个至关重要的理论，基于此衍生出各式各样的网络。Iandola 等［15］提出一种小网络SqueezeNet，在达到AlexNet精度的情况下，只需要AlexNet 中50%的参数。Howard 等［16］提出基于移动端和嵌入式视觉应用的MobileNets 模型，使用深度可分离卷积构建轻量级DNN，结果表明MobileNets 在ImageNet 分类问题上有极佳的性能。Zhang 等［17］为了避免分组卷积带来副作用，设计允许更多通道数的ShuffleNet，使用通道打乱操作来帮助信息在不同的通道间流动，利于编码更多信息。

总而言之，现有的经典神经网络压缩算法在内存占用、运行速度及压缩效果的实验性能上各有优劣。针对以上问题，本文首先系统分析DNN 压缩算法的影响要素，并提出一种基于混合机制的深度神经网络优化算法提升压缩效率，为深度神经网络在有限资源环境下的移动部署提供可行的解决方案。

2 深度神经网络压缩算法的影响要素

本文基于AlexNet，在mini-ImageNet 数据集上，综合考虑压缩算法的结构属性和功能属性，对网络剪枝、线性参数量化、基于K-means 的聚类参数量化、知识蒸馏以及分组卷积五种神经网络压缩算法进行性能评测，并从准确率、压缩比和加速比三个指标进行分析。对比结果如表2 所示。

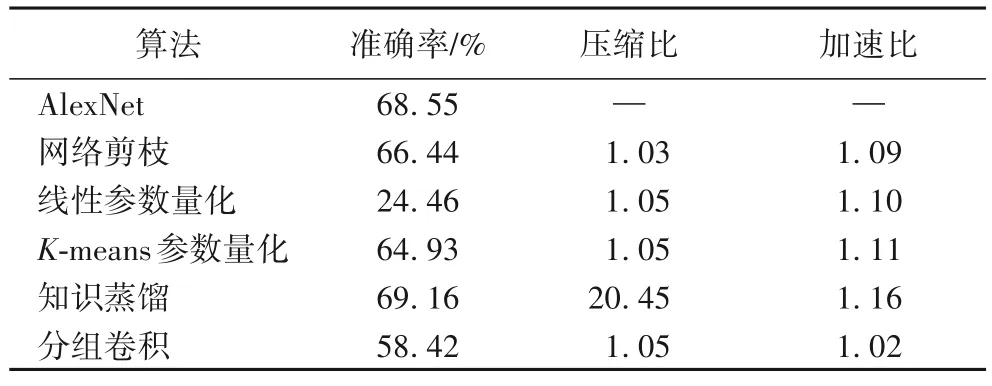
表2 不同压缩算法对AlexNet的压缩结果对比Tab.2 Compression results of different compression algorithms on AlexNet

在进行网络剪枝操作时，首先训练未剪枝的神经网络，设置删减阈值为0.5，通过fine-tune 将剪枝后的模型重新在训练集上训练，以减少网络剪枝带来的损失。若剪枝后网络的准确率变化在5%以内，则结束剪枝操作；反之继续剪枝。经过网络剪枝压缩的神经网络压缩比为1.03，准确率小幅下降，运行速度和压缩程度得到了小幅优化。

线性参数量化和K-means 参数量化都将卷积层参数压缩至4 b，虽然压缩比与加速比相差不大，但线性参数量化会导致准确率过低。因此，本文的混合机制在进行组合时选择K-means 参数量化算法。

知识蒸馏的学生网络构造相对简单，主要由3 个卷积层和1 个全连接层构成。从表3 可以看出，经过知识蒸馏后，网络的准确率相较于原始AlexNet 提高了0.61 个百分点，压缩比达到了20.45，加速比也较其他经典算法表现更出色。同时，可以看出，通过分组卷积调整神经网络结构后，网络的压缩比和加速比也有小幅提升。

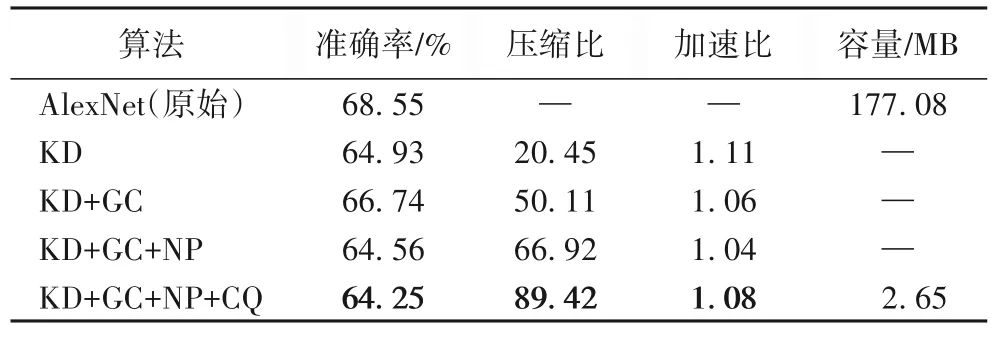
表3 压缩算法实验结果Tab.3 Experimental results of compression algorithms

知识蒸馏通过模型转换将知识迁移到紧凑的模型上，显著提升了压缩性能，说明模型全局（结构）层面的优化对算法具有积极影响。同时，从局部（参数）的角度来看：网络剪枝与分组卷积分别采用参数去繁与参数简化的方法实现末端（参数）的功能优化，提高了算法压缩性能；而参数量化则令多个参数共享数值，使用K-means 参数量化能优化模型的运行速度和空间占用。因此，本文设计了一种融合压缩算法结构与功能特征，自全局向局部优化的神经网络压缩机制。

3 基于混合机制的DNN压缩优化算法

3.1 优化算法模型构建

本文采用知识蒸馏设计一个体量较小的学生网络和基于AlexNet 的教师网络作知识迁移，使学生网络从教师网络中学习教师网络学到的“知识”，再通过结构设计、网络剪枝缩小学生网络的体量大小，并通过参数量化进一步缩小学生网络。本文算法主要的模型结构如图1 所示。

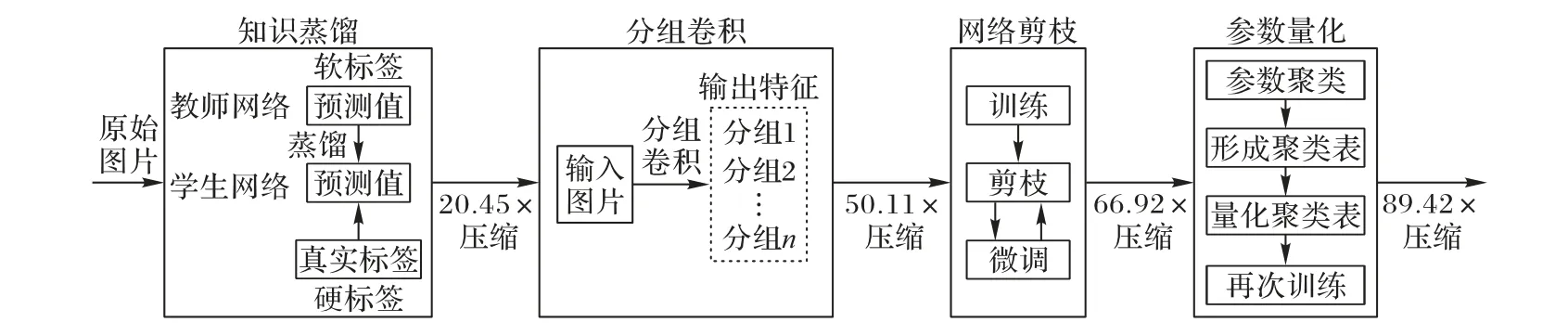
图1 本文算法的模型结构Fig.1 Model structure of the proposed algorithm

3.2 教师网络和学生网络的构建

本文首先基于知识蒸馏压缩算法建立教师网络和学生网络两个神经网络，其中教师网络结构与AlexNet 结构一致，学生网络为3 层卷积层与1 层全连接层简单组合而成的网络。利用这两个网络进行知识迁移，其中教师网络为“知识”输出者，学生网络为“知识”接受者，将学生网络的训练结果与正确标签比对，用式（1）求得cross-entropy 并最小化它的值：

其中：H(A，B)是神经网络A和神经网络B的交叉熵；xi是样本标签；PA(xi)是神经网络A判断结果为样本xi的概率；PB(xi)是神经网络B判断结果为样本xi的概率。

知识蒸馏过程可以大致划分为两个阶段，如图2 所示：第一阶段是训练相对复杂或由多个模型集成的教师网络；第二阶段是训练学生网络，它是参数量较小、结构相对简单的模型。损失函数用式（2）表示，主要由教师网络训练结果经蒸馏后与学生网络训练结果的损失LossSOFT(q，q″)和学生网络训练结果与标签的损失LossHARD(p，q)组合而成。

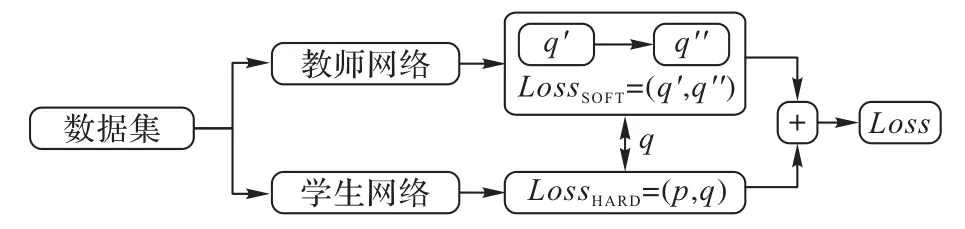
图2 知识蒸馏流程Fig.2 Process of knowledge distillation

其中：p为样本标签；q为学生网络训练结果；q″为教师网络经蒸馏后的训练结果。

学生网络和教师网络对于任何输入都能获得输出，输出经过Softmax 映射后同样能输出对应类别的概率值。与普通Softmax 层不同，知识蒸馏的Softmax 层用式（3）表示，需要添加温度参数，避免输出变为one-hot 形式而损失教师网络所携带的隐藏信息。其中：yi为输出结果；xi为第i个输入；xj为遍历所有输入；T为温度参数。经过知识蒸馏的神经网络效果对比如图3 所示，虽然经过知识蒸馏（Knowledge Distillation，KD）的学生网络（KD）仍不如教师网络，但在测试集上的损失和准确率都优于未经过知识蒸馏的学生网络。

图3 经过知识蒸馏的神经网络的结果对比Fig.3 Comparison of results of neural networks after knowledge distillation

3.3 学生网络的结构设计

完成知识蒸馏后，学生网络已经学习到教师网络所学过的“知识”，其中还包含带有隐藏信息的“暗知识”。此时对学生网络进行结构设计，使它只需要比较少的参数，就能够进一步压缩深度神经网络的空间大小。

利用深度可分离卷积对卷积神经网络进行结构设计，该方法一般分为逐通道卷积和逐点卷积两个步骤，如图4 所示。其中逐通道卷积过程是将卷积核设为平面，设置卷积核数量与输入通道数相等；逐点卷积过程则是将不同卷积核处理的数据连接起来。处理上一步的输出特征图，将新卷积核大小设置为1 × 1 的通道数以得到新输出。此方法能明显减少参数量。设输入通道数为I，输出通道数为O，卷积核大小为K×K，此时参数量减少至这样做之所以能减少参数数量，是相当于在逐通道卷积的过程中共享了参数。

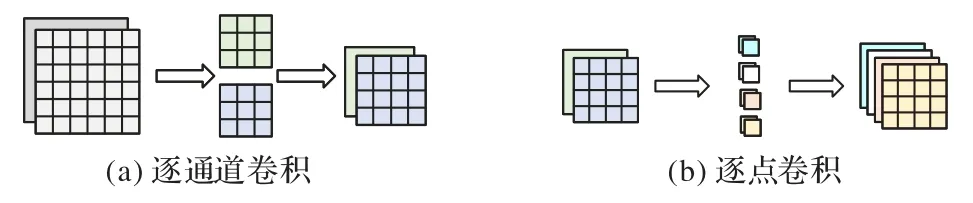
图4 深度可分离卷积Fig.4 Depthwise separable convolution

由于后续还需对学生网络进行网络剪枝，而对卷积层使用深度可分离卷积的方式会对剪枝结果产生较大影响，所以本文采用原理类似的分组卷积予以替换。分组卷积原理如图5 所示，分组卷积输出特征图的每个通道只与输入特征图的部分通道有关，这部分通道即为组。设输入通道数为I，输出通道数为O，卷积核大小为K×K，分为N组，则每一组的输出通道数为，只需要将各分组的计算结果按照通道连接即可，用此方法的参数量为，一定程度上减少了卷积所需参数量。

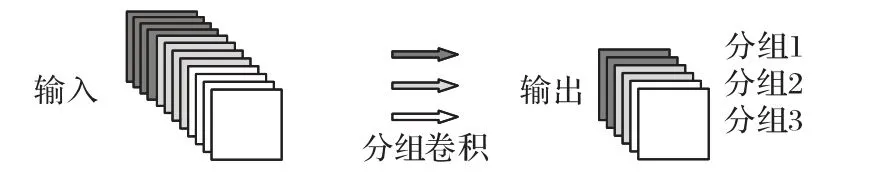
图5 分组卷积Fig.5 Group convolution

3.4 学生网络的网络剪枝

对学生网络进行网络剪枝操作能进一步缩小学生网络的大小，网络剪枝本质是移除深度神经网络中的冗余参数。本文主要以权重为剪枝单元实现非结构化剪枝，对学生网络的网络剪枝流程如图6 所示。

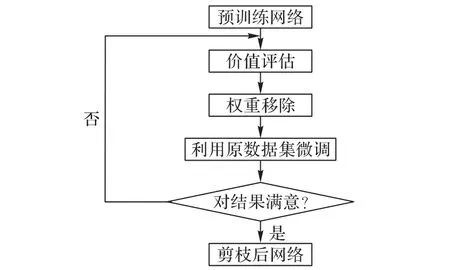
图6 网络剪枝流程Fig.6 Flow of network pruning

首先训练未剪枝的学生网络；其次利用式（4）和式（5）计算L1、L2的取值，移除取值在设定阈值以外的权重；再利用原数据集对剪枝后的学生网络进行训练微调，以减少剪枝所带来的损失；最后判断剪枝后的网络准确率变化是否在5%范围内浮动，若是则结束算法，否则进行二次剪枝。

其中：yi为第i个样本标签；为第i个输出数据；m为样本数。

3.5 学生网络的参数量化

完成知识蒸馏、结构设计、网络剪枝后，对学生网络进行参数量化操作进一步压缩DNN。参数量化有许多不同实现方式：如利用K-means 等算法对神经网络的权重进行类别分簇；也可以将出现频率高的簇用低比特代替，将频率出现低的用高比特代替，如此能减少存储空间，如Huffman encoding算法。

本文主要实现线性量化和基于K-means 的非线性量化两种参数量化方法。线性量化计算便捷，如式（6）所示，设A和W都是类型为float32 的浮点数，将A和W分别量化为int8类型的AQ和WQ后进行计算，能显著提高运算速率，但量化后的AQ和WQ在一定程度上存在损失，a，b，c，d为常数。

基于K-means 的非线性参数量化过程如图7 所示，对学生网络中的权重进行K-means 聚类操作，将同一类别下的权重赋值为该类别的均值，分簇后只需要一个存储类别的Tab1 和一个存储类别与权重映射关系的Tab2 即可表示权重，能够有效地减小所需存储空间。

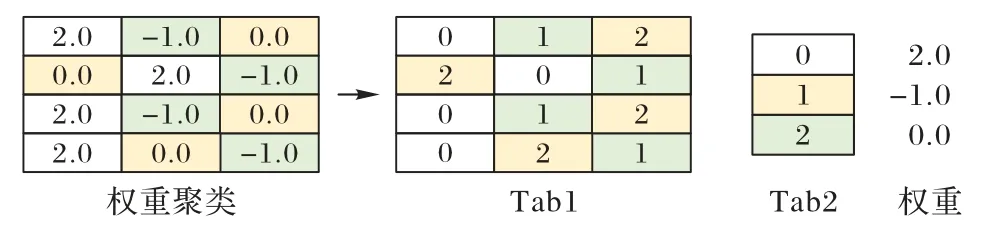
图7 基于K-means的参数量化设计Fig.7 Parameter quantization design based on K-means

4 实验与结果分析

4.1 实验数据集

实验采用mini-ImageNet 数据集（https：//lyy.mpi-inf.mpg.de/mtl/download/Lmzjm9tX.html）。mini-ImageNet 数据集在元学习和小样本学习领域应用广泛，是ImageNet 数据集的子集。

ImageNet 数据集是一个非常庞大的数据库，主要用于对视觉识别的研究。ImageNet 数据集为超过1 400 万张图像标记注释，并给100 万张以上的图像提供了边框，ImageNet 数据集中包含“气球”“轮胎”等20 000 多个类别数据，且每个类别均有不少于500 张图像。训练如此庞大的数据集需要消耗大量计算资源，因此，2016 年GoogLe DeepMind 团队在ImageNet 的基础上提取出了它的子集mini-ImageNet。

DeepMind 团队首次将mini-ImageNet 数据集用于小样本学习研究，mini-ImageNet 数据集自此成为了元学习和小样本领域的基准数据集。mini-ImageNet 数据集内共包含100 个类别，共60 000 张图片，其中每类有600 个样本，每张图片的规格大小为84×84，图片均为RGB 三通道彩色图片。相较于CIFAR10 数据集，虽然mini-ImageNet 数据集更加复杂，但更适合进行原型设计和实验研究。mini-ImageNet 的容量大小为2.86 GB，数据架构如图8 所示，其中images 里为所有的图片样本，train.csv、test.csv 文件内均含两列数据，第1 列为文件名，第2 列为标签。

图8 mini-ImageNet的数据架构Fig.8 Data architecture of mini-ImageNet

4.2 数据预处理

首先对数据集进行划分。如果按照给定的训练集和测试集进行划分，即将100 个类别数据按照类别划分给三个数据集，这并不契合本文的实验需求，因此，首先将所有照片提取出来，通过train.csv 和test.csv 将照片保存到对应标签的文件夹下，即将100 类数据保存到100 个文件夹中，文件夹名为类别名。将数据按照6∶2∶2 的比例划分为训练集、验证集和测试集，三个数据集内均有100 个类别，数据集中每个类别的样本数为划分好的6∶2∶2。数据示例如图9 所示。

图9 数据示例Fig.9 Examples of data

对mini-ImageNet 数据集中的每个样本进行预处理。与MNIST 手写数据集不同，mini-ImageNet 是从原始ImageNet 数据集中选择的一小部分子集，每个子集包含来自不同类别的图像，这些图像可能具有不同的尺寸和宽高比。在使用mini-ImageNet 进行训练和评估时，通常会将所有图像调整为相同的大小，以便于输入到模型中。由于本文主要基于AlexNet 设计算法实验，故统一将图片随机裁剪到224×224 的像素大小，并进行随机水平翻转以达到数据增强的效果，减少过度拟合并提高模型的泛化能力。

4.3 评测标准

实验过程的压缩比Cr和加速比Sr主要效仿失真率而来，利用式（7）和式（8）进行计算。准确率Ar则利用式（9）计算。

其中：M为原模型，M'为经压缩后的模型；λ为原模型占用存储大小，λ∗为经压缩后模型占用存储大小；γ为运行原模型耗时，γ∗为运行经压缩后模型耗时；α为所有预测正确的样本数，α∗为总样本数量。

4.4 实验设计

为了更充分地比较和分析本文算法与已有方法的实验性能，本文的实验设计分为两个步骤：AlexNet 训练与压缩算法性能评测，以实现Benchmark 性能分析。具体过程如下。

1）AlexNet 训练。将mini-ImageNet 数据集按照6∶2∶2 划分为训练集、测试集和验证集进行实验，通过验证集调整选择在训练集得到的最优的结果并应用于测试集，须在训练前对图片统一进行裁剪。经迭代训练得到本文实验的Benchmark 算法。

2）压缩算法性能评测。基于AlexNet 对不同深度神经网络压缩算法及组合算法进行算法性能评测。本文主要考虑了网络剪枝、线性参数量化、基于K-means 的聚类参数量化、知识蒸馏以及分组卷积5 种神经网络压缩算法的组合方法进行实验。

4.5 实验比较与分析

基于以上分析设计，本文基于AlexNet 在mini-ImageNet数据集上进行了实验比较与分析。实验结果如表3 所示，其中：GC（Group Convolution）代表分组卷积，NP（Network Pruning）代表网络剪枝，CQ（Clustering Quantization）代表聚类量化，LQ（Linear Quantization）代表线性量化，KD 代表知识蒸馏。实验结果表明，本文算法（KD+GC+NP+CQ）在压缩后的准确率只降低了6.3%的情况下，压缩后AlexNet 的容量减小了98.5%，压缩性能较优。在准确率损失不严重的情况下，压缩比随着组合压缩算法复杂度上升而增大，其中知识蒸馏显著压缩了神经网络模型，且对加速比的提升有较大优化，分组卷积和网络剪枝的加入很大程度上缩小了模型存储空间，最后对模型进行基于K-means 的聚类参数量化操作，进一步压缩加速模型。图10 展示了AlexNet 在进行网络剪枝时，在不同删减阈值下的准确率损失与压缩比变化趋势。

图10 不同删减阈值情况下的实验结果比较Fig.10 Comparison of experimental results under different deletion thresholds

分析可知，随着删减阈值不断增大，压缩比和准确率损失总体呈上升趋势，当删减阈值为0.5 时出现一个转折点，此时是最佳删减阈值。从理论上而言，在进行网络剪枝时，所删减的网络连接会随着删减阈值的增大而变多，从而使参数的稀疏矩阵中为零的值随之增多，达到减小存储空间的效果。AlexNet 的存储占用随着删减阈值的增加而减小，与理论相同。在经过最佳阈值点0.5 后，AlexNet 在（0.5，0.7］的阈值区间内准确率损失增长速率显著，说明此时神经网络中重要程度高的连接比较多，而重要程度低的连接比较少。

图11 展示了AlexNet 量化为不同比特条件下的准确率损失与压缩比变化趋势。因为在进行K-means 聚类之前是利用随机中心点初始化的，本文选取3 次实验结果的平均值进行分析以避免实验偶然性。

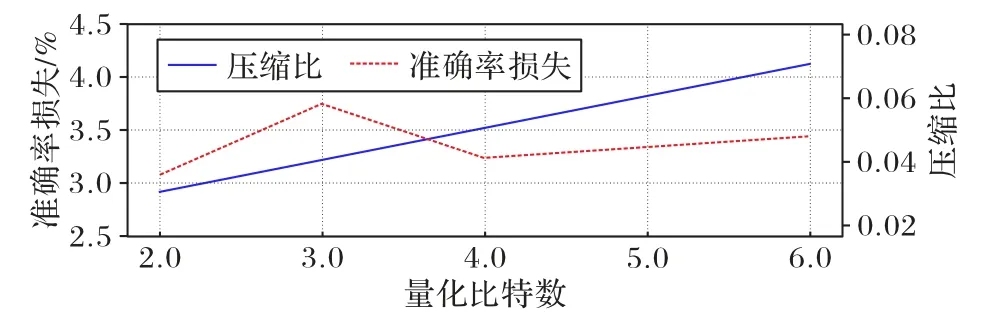
图11 不同量化比特数情况下的实验结果比较Fig.11 Comparison of experimental results under different quantization bit numbers

分析可知，模型的准确率损失首先随着量化比特数增加而上升，在4 b 时出现明显转折点，随后呈现缓慢上升趋势。当量化模型参数为4 b（聚类簇数为16）时准确率损失最小。理论上，在执行参数量化对神经网络进行压缩时，量化比特数越大，占用的存储空间也越少。如图11 所示，AlexNet 的压缩比随着量化比特数上升而稳步上升，与理论结论一致。

图12 展示了AlexNet 在不同分组条件下的准确率损失情况。对AlexNet 使用1、2、4 组不同数量分组进行训练，分析可知，当划分分组数量为2 时，虽然在一定程度上减少了模型参数，但准确率损失比较严重；当划分分组为4 时，能更大程度压缩模型的同时减小准确率损失，也就是保证准确率并减小模型参数存储空间。理论上而言，分组卷积能带来的模型效果要优于标准的卷积网络，因为分组卷积类似于正则所带来的效果，能够减少训练参数的同时增加相邻层之间对角相关性，避免过拟合的现象发生。分析可知，AlexNet 的准确率随分组的数目呈现先减小再增加的趋势，故划分组别为4 能带来更好的压缩效果。

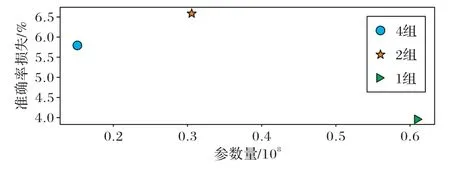
图12 不同分组情况下的准确率损失对比Fig.12 Comparison of accuracy loss under different grouping conditions

5 结语

本文针对深度神经网络因模型存储和计算量大而难移植至嵌入式或移动设备的问题，系统分析了深度神经网络压缩算法影响要素，提出了一个基于AlexNet 的影响要素分析研究框架；在此基础上，提出了一种融合知识蒸馏、结构设计、网络剪枝和参数量化的混合机制的深度神经网络优化压缩算法。实验结果表明，在准确率降低了6.3%的条件下，存储量压缩比达到了89.42，加速比达到了1.08，为深度神经网络在移动设备等有限资源条件下的移动和部署提供了更大的可能性。