基于k-ω 湍流模型的某云爆弹亚音速下二次引信气动特性研究

车淑琴，马俐康，杜云鹏，孙春霞，童亚光，戴 为

（晋西工业集团有限责任公司，太原 030027）

云爆弹是一种高能毁伤弹药[1]，自1966 年美国在越南投下首枚GBU-55B 云爆战斗部以来，云爆战斗部以其独特的作用方式及大面积高效毁伤特点受到世界各军事强国的大力追捧，在世界各军事强国的技术推动下，云爆战斗部取得了快速的发展[2]。而二次起爆型云爆弹会发生二次爆炸，一次释放大量燃料，利用炸药爆炸产生的冲击波将外层的云爆剂抛撒到空中。与空气混合，产生高浓度的云雾气。然后二次引信会再次点火引爆炸药，将含有高浓度云爆剂的云雾气引爆，形成火球并产生气浪，从而达到摧毁建筑物和杀伤人员的目的[3]。

二次引爆的时间很大程度上影响着云雾爆轰产生的威力，引爆时间过早，云雾浓度过大、体积过小，消耗起爆能较多；引爆时间过迟，云雾浓度偏小，容易发生爆燃而非爆轰，爆燃产生的威力远小于爆轰威力，甚至起爆失败。因此，为适应较高终点落速的二次起爆型云爆弹的使用需求，在二次引信与母弹分离后，需要合适的阻力特性，且在减速过程中保持自身稳定飞行，确保二次引信能够在恰当的时间、高度与扩散至最佳浓度的云团实现交会起爆[4]。

通过仿真分析从分离点到起爆点的弹道过程，确定二次引信阻力特征，使得二次引信在特定的时间落入云团中心，二次引信到达预定高度即开始分离，通过增大分离速度实现二次引信减速。采用仿真分析抛撒点到起爆点的弹道过程，确定二次引信分离延时、云雾剂抛撒延时和二次引信起爆延时，使二次引信与云团中心在空间-时间上进行动态匹配交会，在特定时间内实现云团起爆。二次引信阻力特性及稳定性都影响到弹道计算时二次引信减速和飞行结果，故而二次引信阻力特性及稳定性的研究对云爆弹的可靠起爆至关重要。

1 N-S 方程

CFD 数值求解的核心部分是Navier-Stokes（N-S）方程，从方程中可获得流动规律和解决流动问题，在三维直角坐标系下可压缩流体非定常流动的N-S 方程为[5]

N-S 控制方程是所有牛顿流体流动必须遵循的支配方程，然而这些流动所呈现的具体状况千差万别，这是由于定解条件和流体物性的不同而引起的。因此，边界条件的提法及其数学处理在计算流体力学中是一个十分重要的问题。首先，适当的边界条件提法及其数学处理是计算过程稳定的必要条件；其次，边界处理的具体方法可能影响如摩阻、热流等物理量的计算精度；再次，在对一些流动问题的细致模拟中，边界条件将可能对流场内部结构产生影响。总之，对于多尺度物理量现象的直接数值模拟来讲，不仅需要采用高精度、高分辨率的差分格式，而且要求控制边界条件[6-8]。由于k-ε 模型更加适合做主流区计算，而k-ω 模型在近壁面的计算中有较大优势[9-13]，本文中近壁面主要采用k-ω 湍流模型。

2 二次引信气动特性数值仿真计算

为适应云爆弹内部空间需要并增加二次引信进入云团的概率，在云爆弹内部分布4 个二次引信，同时为更大程度地提高二次引信内部空间，将其设计为异形形状。二次引信气动CAD 外形简化后如图1 所示，该二次引信在俯仰、偏航方向具有对称性，二次引信分为弹体及6 个稳定尾翼，弹体剖面为六边形，稳定尾翼翼型为长方形。弹体特征长度为0.548 m，参考面积为0.070 703 974 4 m2。

图1 二次引信模型

2.1 网格划分

该二次引信的CFD 仿真模型是采用商业软件进行模拟数值计算的，采用从上到下的结构体网格划分方法，异形二次引信的局部表面网格模型如图2 所示。计算域外流场网格模型如图3 所示。计算网格采用六面体网格，根据尺寸比例在弹体外围设置一个绕流流场，第一层边界层网格厚度为5×10-6m，网格增长率设定为1.5 以控制网格增长速度，避免网格增长过快导致计算发散，当使用k-ω 湍流模型时，其使用壁面模型法，要求y+=1，近壁面网格层数为15 层，由于云爆弹云爆剂抛撒的特殊性，对抛出二次引信速度区域进行限制，选取表1 中的参数作为计算工况。

表1 计算工况组合

图2 二次引信表面网格

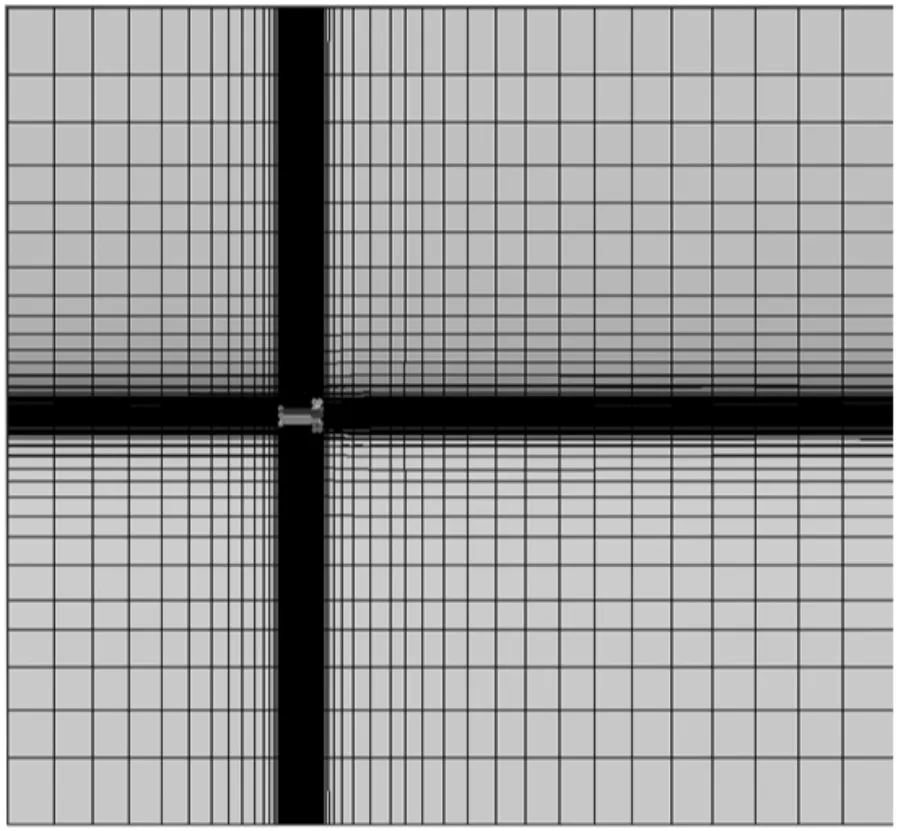
图3 计算域外流场网格

2.2 计算求解

用网格划分软件对计算网格质量进行检查并优化，确认无误后输出网格文件。该模型的计算网格角度Angle 27°以上，Determinant 3×3×3 质量0.5 以上，网格夹角歪斜度Equiangle Skewness 0.2 以上。将网格导入计算软件中后，再一次检查网格质量，显示最小体积网格尺寸大于0 即可（无负体积网格）；使用密度耦合求解器；选择k-ω 湍流模型；运用理想气体介质，气体黏度满足萨兰德定理；避免边界条件选择压力远场边界条件；差分格式采用动量、湍流动能及湍流耗散率均选用二阶迎风格式；参考压强使用标准大气压；采用隐式算法，其余默认；定义监视器，进行20 000 步的迭代计算。作者运用上述设置方法对某现有模型进行计算，并与风洞试验结果进行对比分析，其阻力系数、升力系数、俯仰力矩系数等误差均控制在5%以内，说明该方法计算具有一定的准确性和可靠性。

3 气动特性计算结果及分析

二次引信扰流外流场域压力云图及二次引信弹身上的压力云图如图4、图5 所示。由图5 可知，二次引信端头和翼梢前端所受压强最大。

图4 外流场压力云图

图5 二次引信表面静压

轴向力系数、法向力系数与阻力系数、升力系数的换算关系如下

式中：CD 为阻力系数，CL 为升力系数，Cz 为侧向力系数，CA 为轴向力系数，CN 为法向力系数，CZ 为横向力系数[14]。

3.1 升力特性分析

在侧滑角为0°时，0°、2°、4°、6°、8°、10°和12°攻角下，进行不同马赫数下的仿真计算，得到升力系数变化曲线如图6 所示，由图6 可知，该二次引信升力系数随攻角增大而增大，并且其升力系数受马赫数影响很小，法向力随攻角呈现近似线性变化规律，符合空气动力学基本规律。

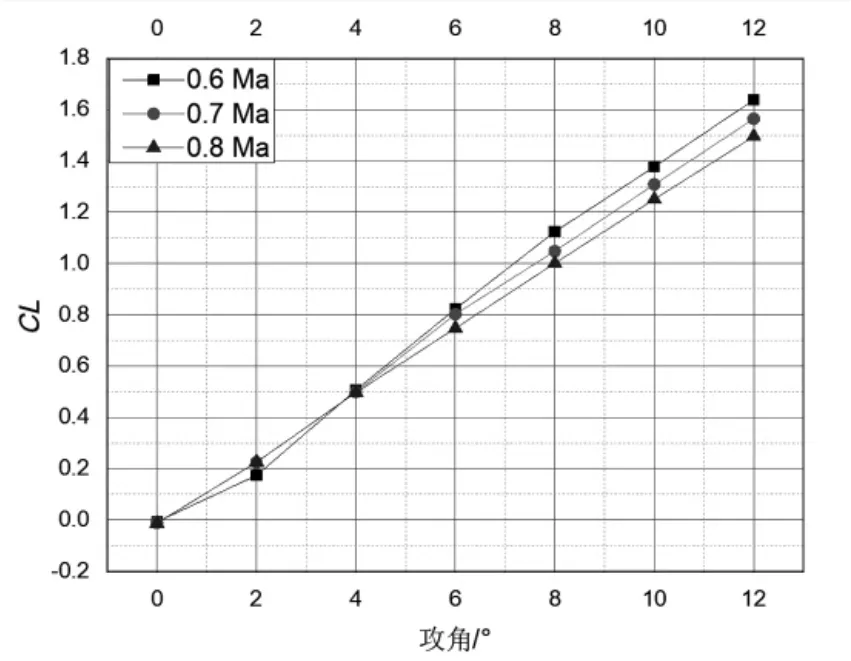
图6 二次引信升力系数随攻角、马赫数变化曲线

3.2 阻力特性分析

在侧滑角为0°时，在0°、2°、4°、6°、8°、10°和12°攻角下，进行不同马赫数下的仿真计算，得到阻力系数变化曲线如图7 所示，由图7 可知，该二次引信阻力系数在相同攻角下，随马赫数的增大而增大；在相同马赫数下，该二次引信阻力系数随着攻角的增加缓慢增长，但增长较小，说明阻力系数受攻角影响较小。

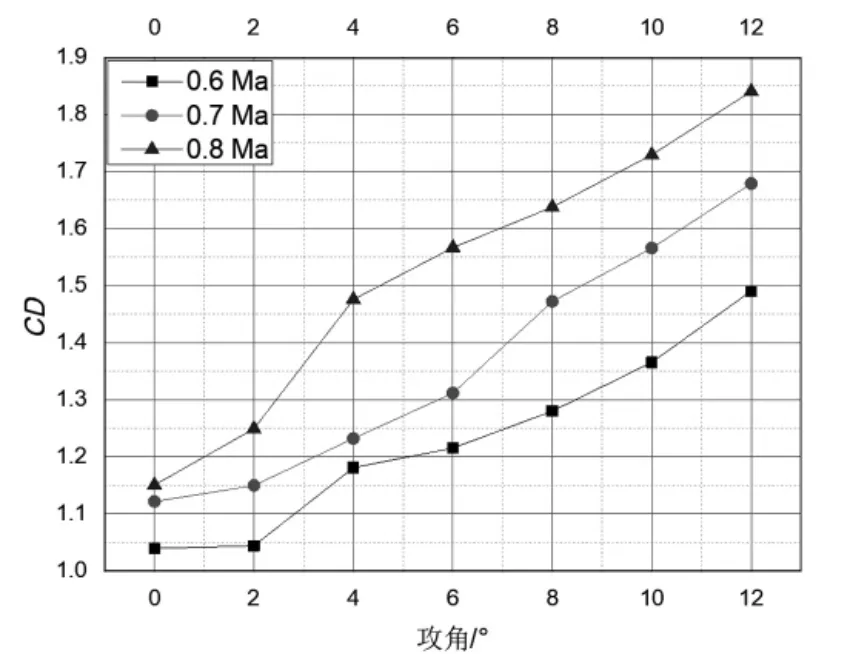
图7 二次引信阻力系数随攻角、马赫数变化曲线

3.3 侧向力特性分析

在攻角为0°时，在0°、2°、4°、6°、8°、10°和12°侧滑角下，进行不同马赫数下的仿真计算，得到侧向力系数变化曲线如图8 所示，由图可知，该二次引信侧向力系数受马赫数影响较小，但是受侧滑角影响较大，侧向力系数随着侧滑角的增大而增大，呈现近似线性变化规律，符合空气动力学基本规律。

图8 二次引信侧向力系数随侧滑角、马赫数变化曲线

3.4 俯仰力矩系数特性分析

该二次引信俯仰力矩系数（对质心0.510 3）随攻角、马赫数变化的曲线如图9 所示，可以看出，俯仰力矩系数随攻角变化并非线性的，且俯仰通道是静稳定的。0～6°攻角时，随着攻角增大，俯仰力矩系数增大较快；攻角为9～12°时，随着攻角增大，俯仰力矩系数增加较慢。

图9 二次引信俯仰力矩系数随攻角、马赫数变化曲线

3.5 偏航力矩系数特性分析

该二次引信偏航力矩系数（对质心0.510 3）随侧滑角、马赫数变化的曲线如图10 所示，可以看出，偏航力矩系数随攻角变化是线性的，且偏航通道是静稳定的。

图10 二次引信偏航力矩系数随侧滑角、马赫数变化曲线

4 结论

本文通过将某云爆弹亚音速下二次引信气动外形作为研究对象，应用商业数值仿真计算软件对模型进行计算，并对计算结果进行分析。计算结果表明，在0.6～0.8 Ma 下，该异形二次引信阻力系数随着马赫数的增大而增大，阻力系数受马赫数影响较大，升力系数随着攻角的增大呈线性增大，阻力系数受马赫数影响较大，侧向力系数随侧滑角的增大呈线性增长；在俯仰通道和偏航通道都是静稳定的，不排除计算误差的情况下，俯仰方向静稳定度在13%左右，偏航通道静稳定度在17%左右，根据以往飞行经验分析，无控情况下，静稳定度达10%左右方可满足实际使用需求，所以俯仰方向和偏航方向的静稳定性可以满足使用需求。研究结果为非常规弹丸弹道特性的深入研究提供了参考和依据。