对角互补模型分类例析

⦿江苏省宝应县实验初级中学 顾啸敏

初中数学里有诸多几何模型,如手拉手模型、角含半角模型、倍长中线模型、对角互补模型等,它们在中考压轴题中频频出现,综合考查学生基本几何知识以及分析、综合、探究的能力,因其变化的图形中往往蕴含着某些不变的关系,而某些变化的关系里又蕴含着不变的解题规律,所以受到了命题者的青睐.本文中重点就“对角互补型”几何模型进行分类例析.

1 90°的全等型

90°的全等型是指相对的两个角都是90°,其中一个直角顶点在另一个直角的角平分线上,我们可以得到相等的线段、线段的和差关系及图形面积之间的关系.此类型的基本图形如图1-1与图1-2,它们的已知条件均为∠AOB=∠DCE=90°,OC平分∠AOB.

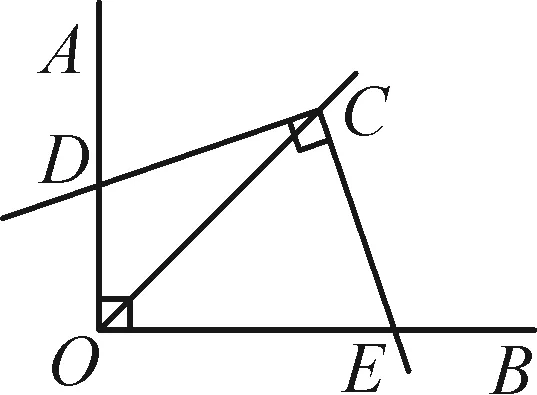
图1-1

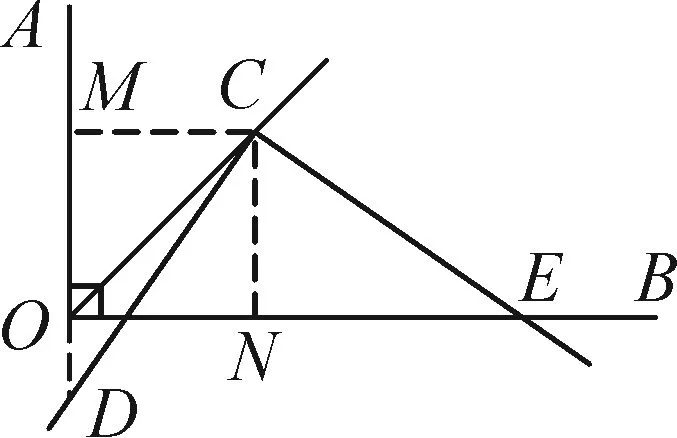
图1-2

例1如图2-1,四边形ABCD被对角线BD分为等腰直角三角形ABD和Rt△CBD,其中∠BAD和∠BCD都是直角,另一条对角线AC的长度为2,求四边形ABCD的面积.

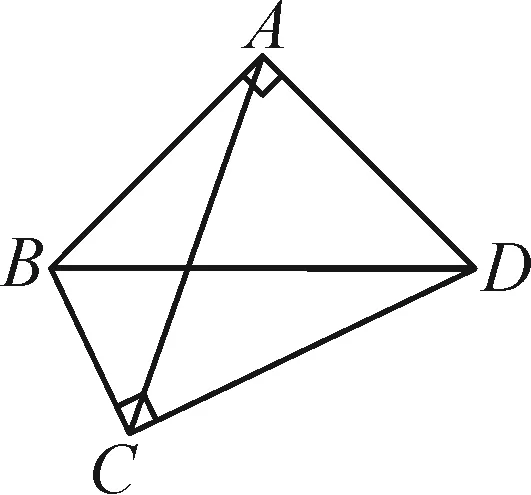
图2-1

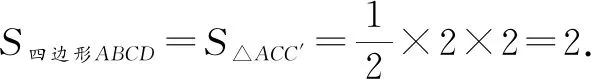
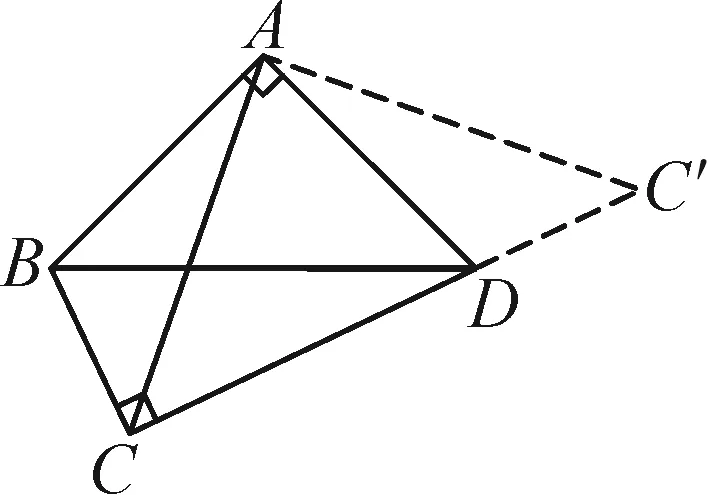
图2-2

评注：本题的图形就是“对角互补模型”,且相对的两角均为90°,此时四边形的面积等于两直角顶点连线平方的一半.

2 120°的全等型

120°的全等型是指相对的两个角分别为120°和60°,其中一个角的顶点在另一个角的平分线上,我们也可以得到相等的线段、线段的和差关系、图形面积关系.此类型的基本图形如图3-1与图3-2,已知条件均为∠AOB=2∠DCE=120°,OC平分∠AOB.

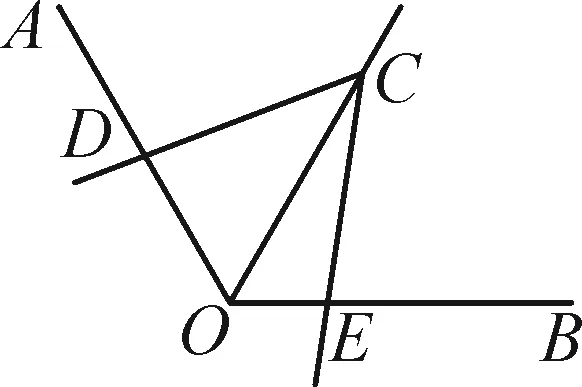
图3-1

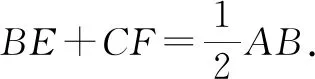
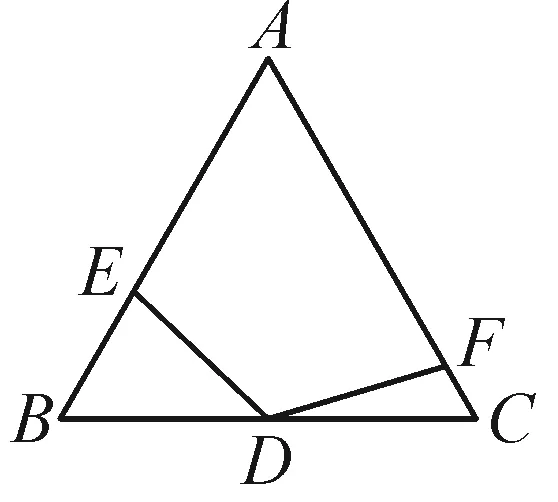
图4-1

解析：过点D作DM⊥AB于点M,作DN⊥AC于点N,如图4-2,则∠AMD=∠BMD=∠AND=∠CND=90°．又∠A=60°,所以

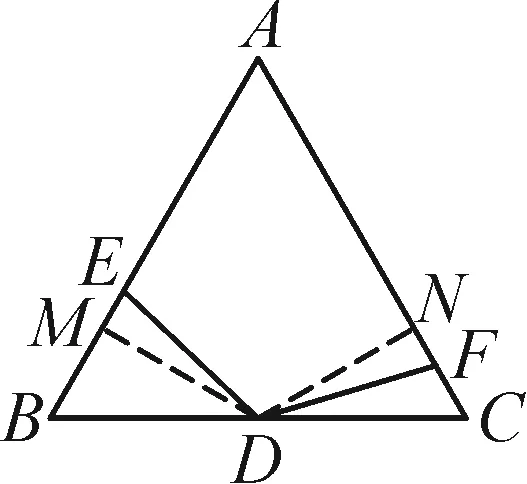
图4-2

∠MDN=360°-60°-90°-90°=120°．

又∠EDF=120°,所以∠MDE=∠NDF．

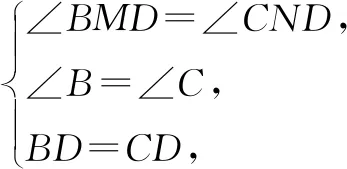
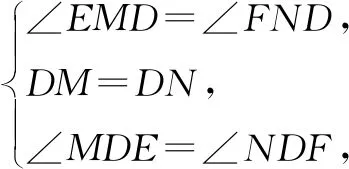
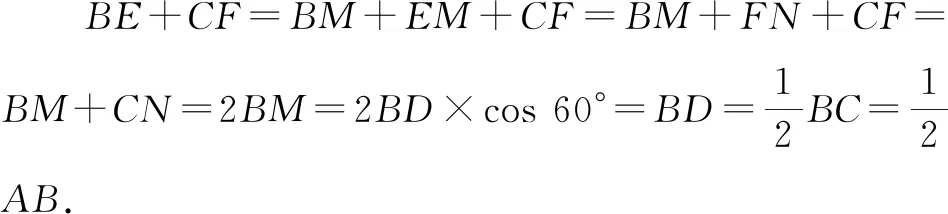
评注：本题属于“对角互补模型”,且对角度数分别为60°和120°,由于D是底边中点,根据“三线合一”可知点D仍在60°角的平分线上.本题虽然没有使用原模型的结论,但仍使用了原模型的思路,即过一个角的顶点作另一个角两边的垂线,从而构造全等三角形.

3 任意角全等型

任意角全等型是指在对角的四边中,相对的两个角只有互补关系,没有特殊的度数,其中一个角的顶点在另一个角的平分线上,我们仍可以得到一些有益的结论.基本图形如图5-1与图5-2,它们的已知条件均为∠AOB=2α,∠DCE=180°-2α,OC平分∠AOB.

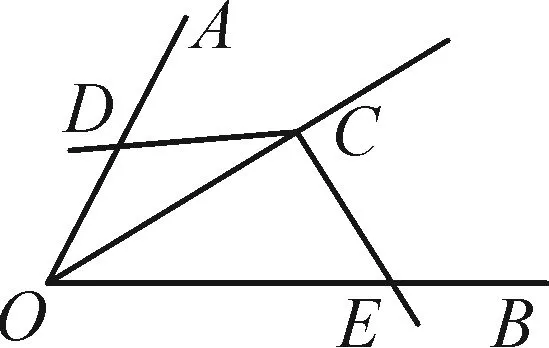
图5-1

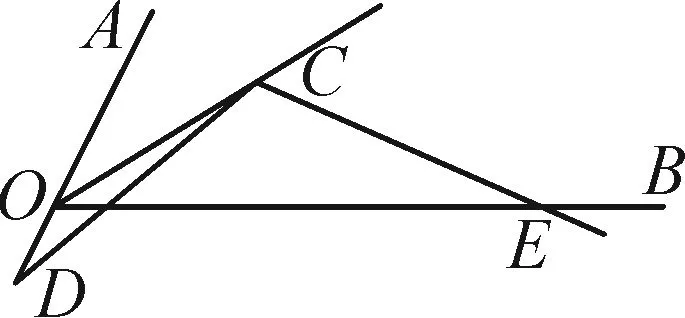
图5-2

对于图5-1,有结论:CD=CE;OD+OE=2OC·cosα;S△OCD+S△OCE=OC2·sinα·cosα.

对于图5-2,有结论:CD=CE;OE-OD=2OC·cosα;S△OCE-S△OCD=OC2·sinα·cosα.

例3已知△ABC是⊙O的内接三角形,AB=AC,在∠BAC所对弧BC上任取一点D,连接AD,BD,CD．

(1)如图6-1,如果∠BAC=120°,那么BD+CD与AD之间的数量关系是什么?写出猜测并加以证明.

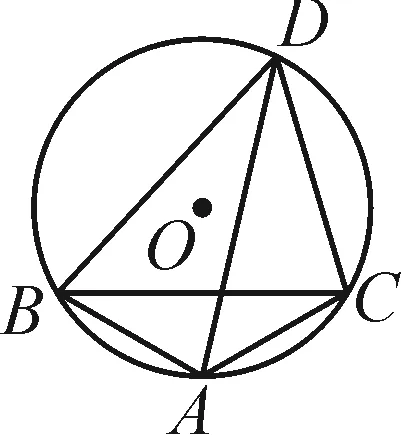
图6-1

(2)如果∠BAC=α,写出BD+CD与AD之间的数量关系并证明.

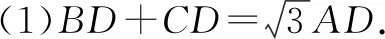
理由如下:延长DB到E,使得BE=DC,连接AE,过点A作AF⊥BD于点F,如图6-2.

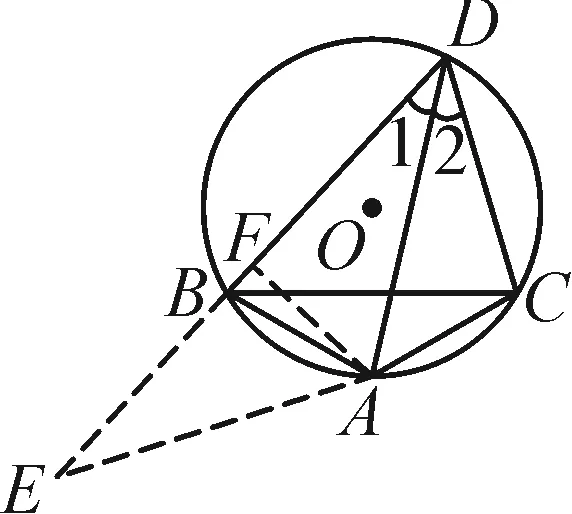
图6-2

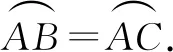
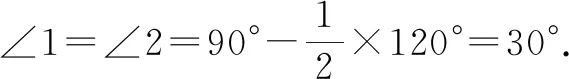
所以∠2=∠E,即∠E=∠1,则AE=AD.

于是DF=EF,从而DE=BD+CD=2DF.

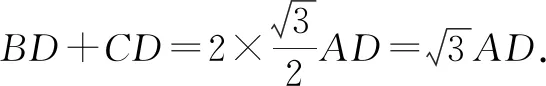
(2)略．

评注：当特殊的度数换作任意角时,它的结论也就更一般了,我们也能看出这种模型的本质所在,但解题思路基本不变,即作垂线、延长截取构造全等三角形.

“对角互补型”这里讲述的是全等型的,即一个角的顶点刚好在另一个角的平分线上.其实,对角互补型的几何模型还有相似型的,即一个角的顶点并不在另一个角的平分线上,有兴趣的同学可以继续探究.只要我们在学习过程中认真总结与反思做过的试题,并掌握一些基本的数学模型,这样在解答数学问题时就能做到得心应手,游刃有余.