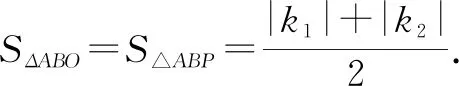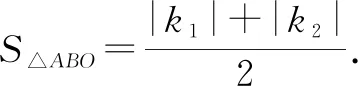巧用反比例函数k的几何意义模型解题
2023-09-27重庆市九龙坡区杨家坪中学郑天顺
⦿重庆市九龙坡区杨家坪中学 郑天顺
在数学解题教学中,教师既要讲解解题思路,更要培养学生的数学思想、模型意识、几何直观理念,让学生学会利用数学模型解决数学问题.本文中将对反比例函数k的几何意义模型解题进行简要分析.
1 利用反比例函数面积不变性模型解题
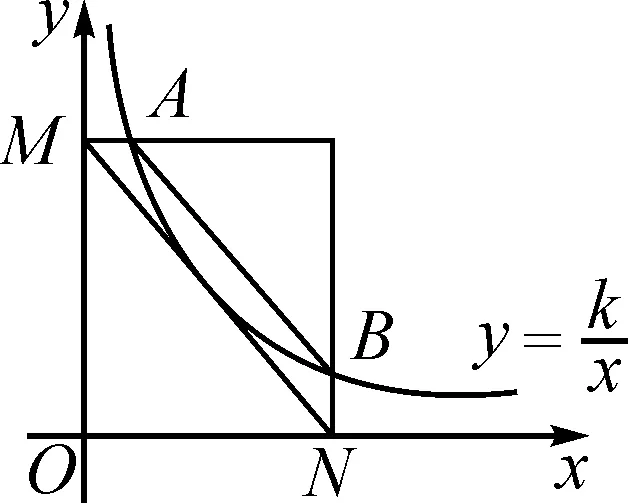
反比例函数面积不变性指的是过反比例函数图象上的任意一点分别作x轴与y轴的垂线,它们与坐标轴形成的矩形面积为定值|k|(如图1所示),即S矩形ABEO=S矩形DOFC=|k|.
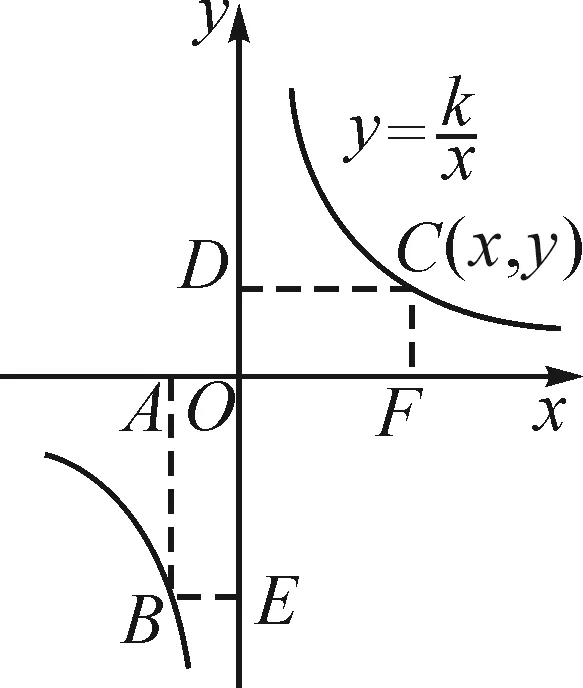
图1
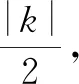
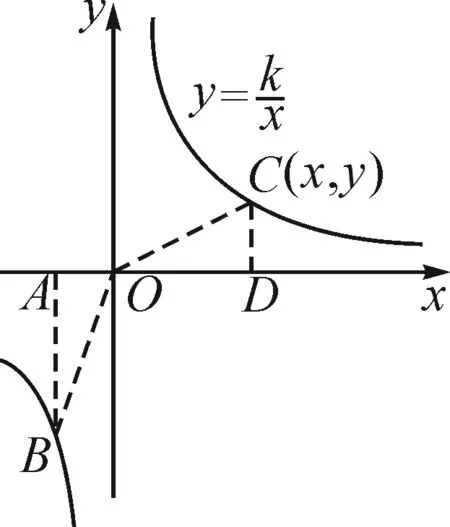
图2
2 利用反比例函数面积公式模型解题
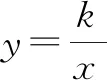
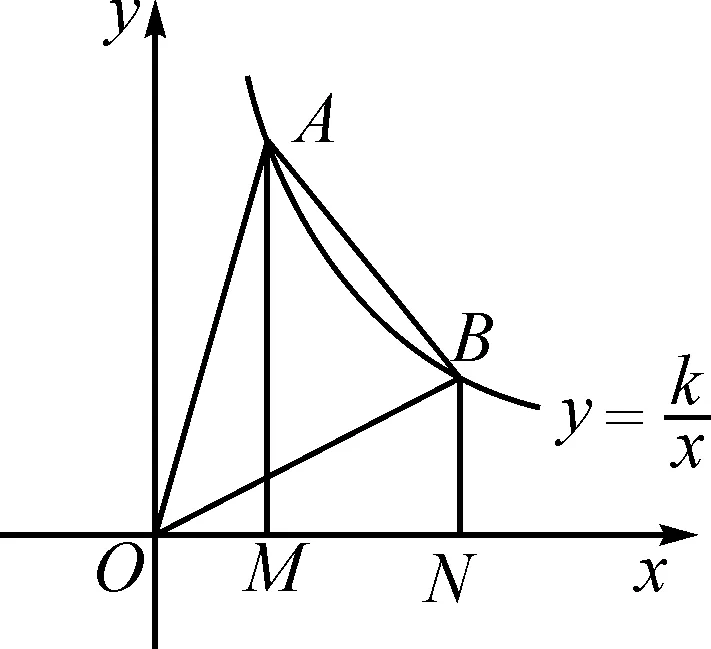
图3
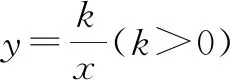
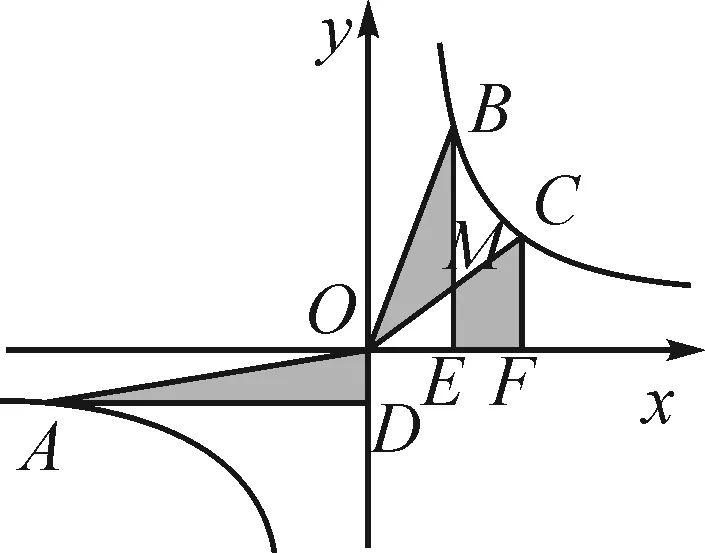
图4
A.S1=S2+S3B.S2=S3
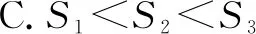
分析:由模型1和模型2的结论,可知
由S△BOE-S△OME=S△COF-S△OME,得S2=S3.
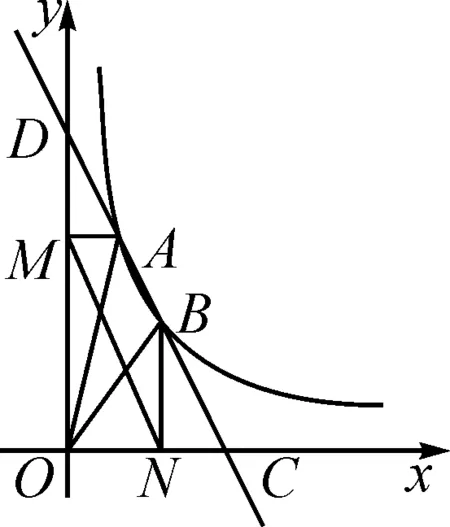
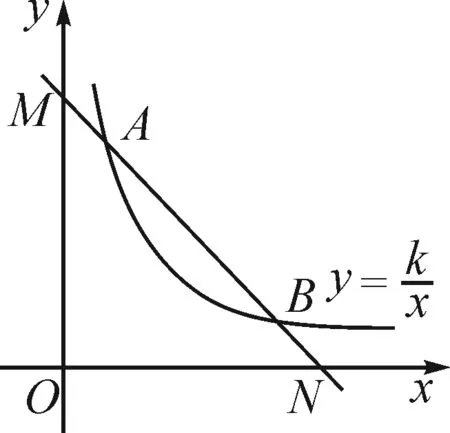
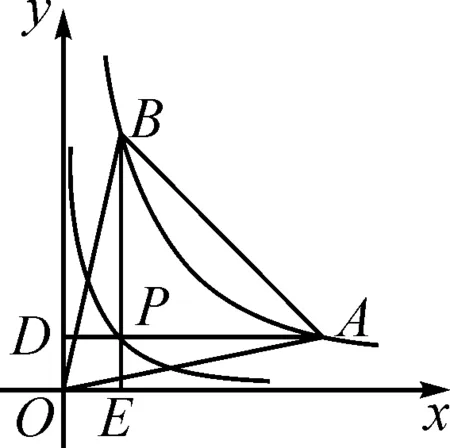
所以S2=S3 反比例函数平行性质模型指的是过反比例函数图象上的任意两点分别作x轴与y轴的垂线,如图5,则AB与MN一直保持平行关系,即AB//MN.反比例函数平行性质模型可有效解决位置、面积等方面的问题. 图5 图6 A.1 B.2 C.3 D.4 分析:结论①,从反比例函数的平行性质模型来看,四边形DMNB与四边形AMNC均为平行四边形,所以BD=NM=AC,AM=CN,所以AD=BC.又∠AMD=∠BNC=90°,所以ΔAMD≌△CNB,故①正确. 结论②,从平行性质模型来看显然正确. 结论③,过点O作CD的垂线,△AOD与△BOC等底同高,面积相同. 结论④,四边形DMNB与四边形MNCA只能确定一组对边相等,故周长并不一定相等. 故选答案:C. 反比例函数等线段性质模型指的是过反比例函数图象上的任意两点作直线,并使这条直线与坐标轴相交,若设相交点分别为M,N,则AM=BN(如图7与图8). 图7 图8 图9 (1)求k的值; (2)连接OA与OB,若点P的横坐标是2,求△AOB的实际面积; (3)若直线AB与x轴交于点M,与y轴交于点N,试证明AM=BN. 分析:(1)显然k=10. 又∠NGB=∠AFM=90°,则△NGB≌△AFM,所以AM=BN. 本题第(3)问还可以先求证S△NOB=S△AOM,再利用等高证明AM=BN,或在Rt△NGB与Rt△AFM中利用勾股定理进行求解,从而论证AM=BN. 图10 (1)若直线AB与x轴或y轴平行,则S矩形ABNP=|k1-k2|. 图12 图13 图15 图16 在数学教学过程中,需注重学生解题思维、创新意识的培养,提高学生应用数学模型的能力.反比例函数k的几何意义模型有很多,如面积不变性模型、面积公式模型、平行性质模型等,在解决数学问题的过程中,让学生了解各种模型的应用方法,从而提高解决问题的能力.3 利用反比例函数平行性质模型解题
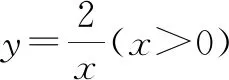
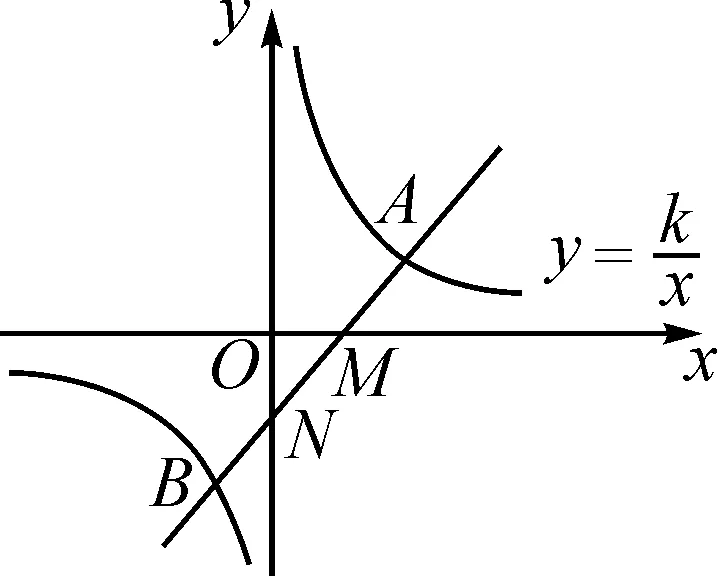
4 利用反比例函数等线段性质模型解题
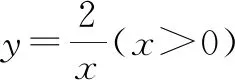
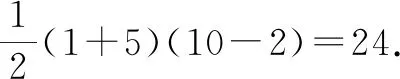
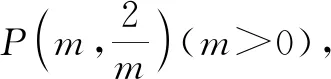
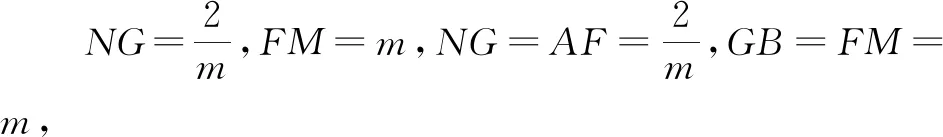
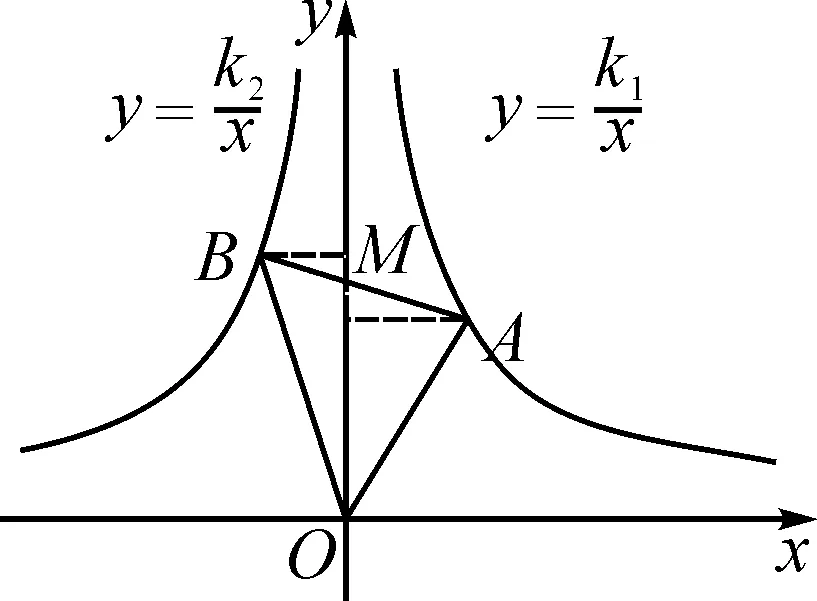
5 利用反比例函数之同侧双曲模型解题
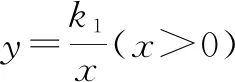
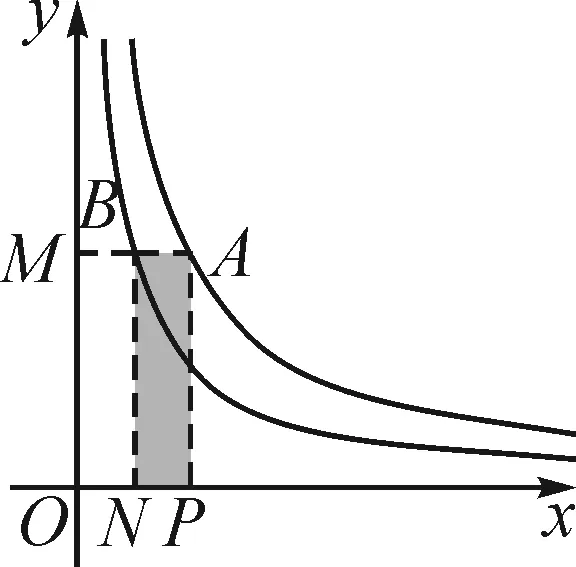
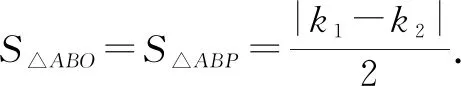
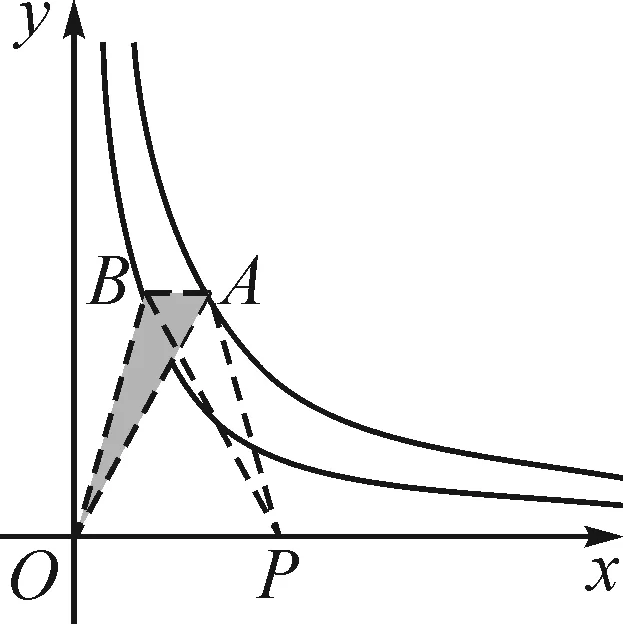
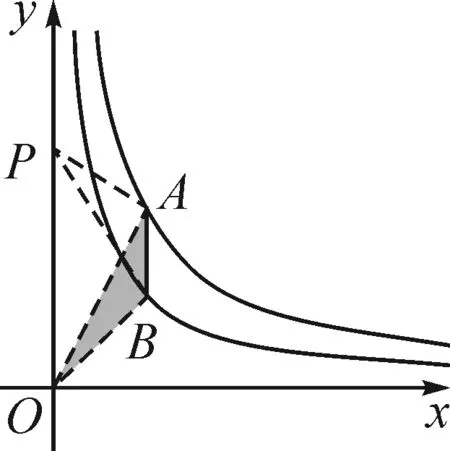
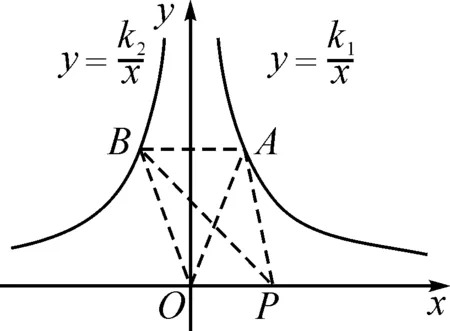
6 利用反比例函数之异侧双曲模型解题