“构造辅助圆”在初中数学解题中的灵活运用

⦿ 吉林师范大学数学与计算机学院 王 雪

“构造辅助圆”是指在原有的几何图形上,构建一个辅助圆,利用圆的特性来完成题目的解答.通过辅助圆的构造,能够将几何题目中较为繁杂的已知条件进行集中处理,同时能够发现几何图形中的隐藏条件,利用对这部分条件的分析,快速解决问题.本文中结合实例,帮助学生明确辅助圆的应用环境,以及针对不同题型如何构造辅助圆.

1 “构造辅助圆”解决数学问题的应用现状

目前初中生在解题的过程中,较少应用辅助圆,且应用效果不理想.在几何题的解答过程中,辅助线的应用是比较常见的,但是有部分题目通过辅助线来解答依旧存在难度,甚至需要多条辅助线才能完成,如果学生用这种方法应对选择题和填空题,就会浪费大量的时间.而应用辅助圆则可以为相关问题披上圆的外衣,这样就可以依据圆的性质进行解题,从根本上起到化繁为简的作用[1].

2 “构造辅助圆”解决数学问题的实际案例

2.1 辅助圆在求线段长度的几何问题中的应用

在解决求线段长度的几何问题中,通常是利用相同端点的线段构造辅助圆,以端点作为圆心,选取相等的线段作为半径或直径,完成辅助圆的构建后再利用圆的基本性质求解线段长度[2].

解析：由AE∥CD,得∠BDC=∠DBE.

由AB=AC=AD=AE,将点D,C,B,E视为圆上的点构建辅助圆,如图1.于是弦DE与弦BC的长度相等.

图1

因为EB为辅助圆的直径,所以∠EDB=90°.

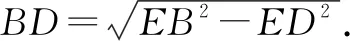
2.2 辅助圆在求度数的几何问题中的应用

在解决求度数的几何问题中,通常可以将公共点作为顶点,作三角形的外接圆.在构建辅助圆的过程中要将三角形与辅助圆建立明确的关系.

例2如图2所示,△ABC为等腰三角形,且AB=AC,直线AP为△ABC外侧直线,点B与点D关于AP轴对称.

图2

求证:∠1=∠2.

证明：∵点B,D关于直线AP对称,

∴直线AP为线段BD的垂直平分线.

∴△ADB为等腰三角形.

∴AD=AB=AC.

故可以AC为半径,点A为圆心,构建如图3所示的辅助圆.

图3

∵P为BD中点,且AP为过点E的直线,

∴△DEB为等腰三角形.

∴DE=BE.

∴∠EDB=∠EBD.

∴∠2=2∠EDB.

又∠1=2∠CDB(同弧所对的圆心角是圆周角的2倍),

∴∠1=∠2.

2.3 辅助圆在求图形面积问题中的应用

在数学中考题中,涉及面积的题型也很多,当题目条件较多且分散的几何图形很难运用面积公式时,可以尝试构建辅助圆,利用圆的基本性质以及圆的面积公式进行计算[3].

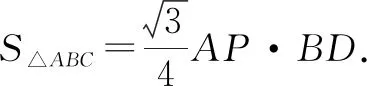
图4

解析：依题意可知AB=AC=BC=AD,构建以点A为圆心,AB为半径的圆,得到如图5所示的辅助圆.

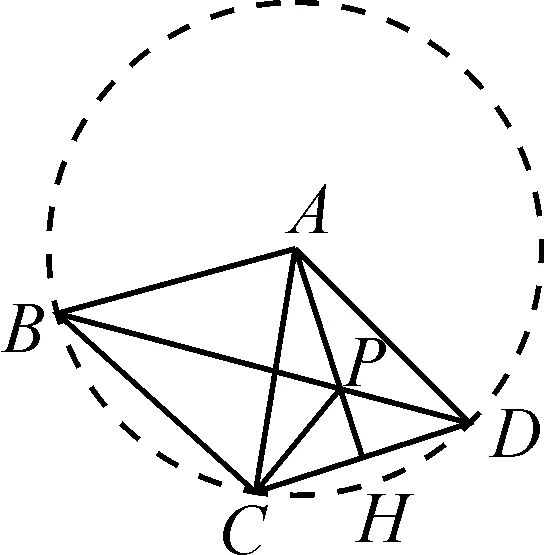
图5

∵△ABC为等边三角形,

∴∠BAC=∠ACB=∠ABC=60°.

又∠BCP=90°,∠BCA=60°,

∴∠PCA=∠CDB=30°.

∴△BCD∽△APC.

∴BC∶AP=BD∶AC.

又BC=AC,

∴BC2=AP×BD.

2.4 辅助圆在求线段比或面积比问题中的应用

图形中的某两条线段成比例或图形面积成比例这类题型是中考的难点和重点.利用辅助圆则可以结合圆的性质,通过圆中的线与角的关系进行求解.构建辅助圆时,要将有关线段置于辅助圆的关键位置,例如,可作为直径、半径或弧所对的弦.这样容易发现线段之间的关系,从而更加简便地进行解答[4].

例4在Rt△ABC中,AC=BC,∠ACB=90°,P是CB延长线上的一点,BP∶BC=k,已知0≤k≤1,过点B作AB的垂线,过点P作AP的垂线,使两条垂线相交于点Q,且AP=PQ,连接AQ,求△ABC与△APQ的面积比.

分析：根据已知条件分析,△APQ的面积较难求解,所以可以根据△APQ来构建辅助圆.

解析：以AQ为直径,AQ的中点O为圆心,构建如图6所示的辅助圆.

图6

∵AP=PQ,且∠APQ=90°,

∴△APQ为等腰直角三角形.

设BC=AC=m.

∵BP∶BC=k,

∴BP=km,PC=(k+1)m.

2.5 辅助圆在求线段极值问题中的应用

辅助圆在求线段极值问题中有着广泛的应用,特别是在数学竞赛中经常遇到.

例5在边长为4的正方形ABCD中,P为对角线BD上的一个动点,且与点B,D不重合,连接AP,过B作AP的垂线,垂足为H,连接DH,求线段DH的最小值.

分析：由于无论点P如何运动,AB的长度都不会改变,因此可以AB为直径,AB的中点E为圆心构建辅助圆,通过圆确定点H的运动轨迹.

解析：取AB中点E,连接DE,构建如图7所示的几何图形,可得

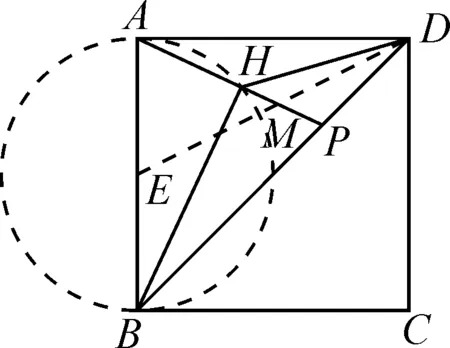
图7

综上所述,“构造辅助圆”在初中数学解题中的广泛应用,不仅包含大量的几何问题,而且部分代数问题中也可使用.构建辅助圆时,要结合题目的具体情况,根据四点共圆的条件确定辅助圆.通过辅助圆在不同类型几何问题中的应用,明确构建辅助圆在初中数学解题中的可行性与实用性,通过辅助圆的灵活应用,提升学生的实际解题能力.