一题诱发 拓展利用 激发联想 促进迁移——探索含45°角问题的研题训练

⦿ 甘肃省定西市临洮县椒山初级中学 杨建霞

数学问题是启发学生思维的源泉.教师在讲解问题的过程中,只有抓住问题突破的方向,找到恰当的方法,才能正确启发学生探究准确的思维路径,在此基础上引领学生及时总结相关解题方法与思路,将数学方法转变为数学思想,再将数学思想沉淀为数学能力,从而转化为数学综合素养,至此,所训练的问题才能真正凸显其价值[1].

波利亚在《怎样解题》一书中说过这样的话:“教师最重要的任务之一是帮助学生分析问题,挖掘问题本质,寻求解题线索,辨析解题方法,有效地帮助学生提升分析和解决问题的能力.”

本文中以一道含有45°角的几何问题为例展开研究分析,彰显问题价值.

1 问题呈现

图1

2 问题思考

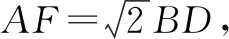
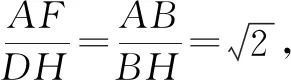
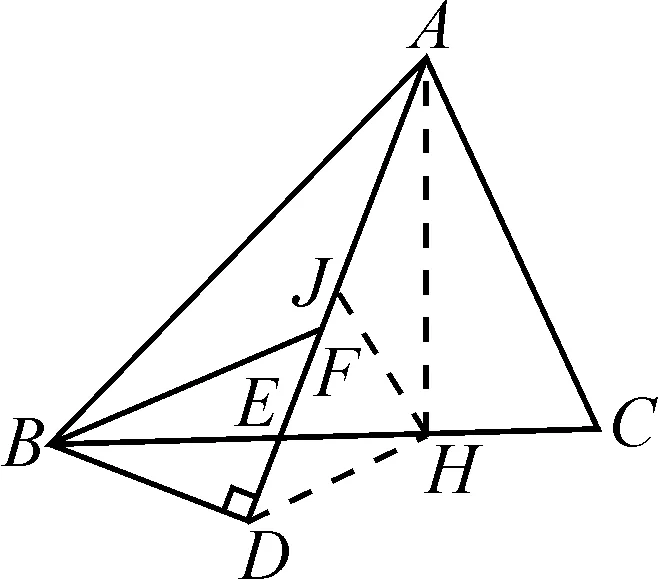
图2

初步结论:从上述问题的解析过程来分析,遇到45°的条件时往往可以构造等腰直角三角形,利用等腰直角三角形的三线合一或者基本性质等展开进一步推理,再结合相关的条件构造全等三角形或者相似三角形,进而解决边之间的关系或角度相等等问题.

3 拓展利用

如图3,在Rt△ABC中,∠C=90°,且满足AC>BC,BD平分∠ABC,点E在BC上,∠EDB=45°,若BE=5CE,CD=3,试求AB的长.

图3

分析：本题条件中显然凸显的是∠EDB=45°,根据已知经验,怎么构造等腰直角三角形呢?有几种可能性,其一过点E作BD的垂线,其二是过点B作DE的垂线.通过分析可以发现,前者在推理过程中与已知条件联系不上,故可考虑后者.如图4,作BF⊥DE,交DE的延长线于点F,FN⊥BC于点N,FM⊥AC于点M,DH⊥AB于点H,连接CF.由△DMF≌△BNF,推理得到四边形MCNF是正方形.设CE=a,则BE=5a.根据边之间的关系可进行突破、解答[2].

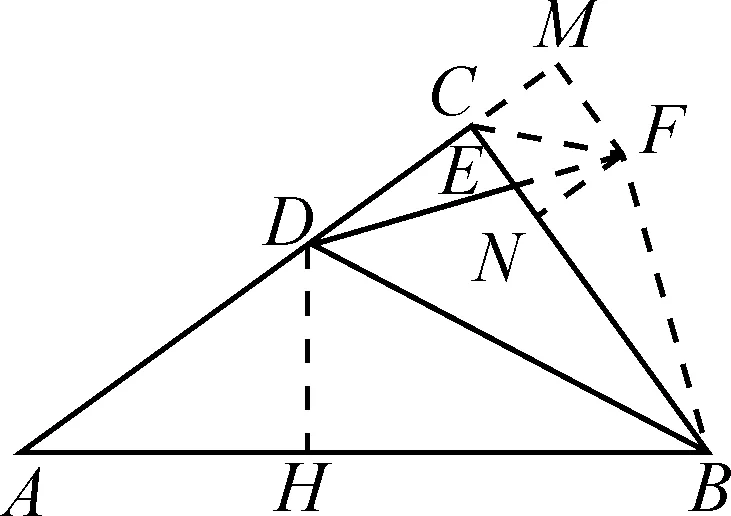
图4

激发联想:只考虑简单的45°,可以直接构造等腰直角三角形,从而找到问题的突破口,作出相关解答.若出现和为45°或者差为45°的情况,又该怎么处理呢?

例如,如图5,在△ABC中,AB=AC,∠BAC=90°,D为平面内的一点.当点D在△ABC的外部,且满足∠BDC-∠ADB=45°,请你证明线段CD与AD的数量关系.

图5

本题中给出的条件是∠BDC-∠ADB=45°,这样的条件显然无法直接利用,根据上述问题给定的一种想法,可以在∠ADB外构造新的45°,这样就能满足∠BDC=∠ADB+45°.如图6,在边AD外直接构造等腰直角三角形,即过点A作AE⊥AD,且AE=AD,连接DE,CE,证△BAD≌△CAE(SAS),得∠ABD=∠ACE,再证△DOC≌△DOE,得CD=ED,即可解决问题.

图6

结论升华:结合上面几个问题的具体分析,我们发现如果遇到几个角的差为45°角的问题时,可以根据相应两个角的位置,重新构造等腰直角三角形,变差为和,再结合相关条件构造全等三角形或相似三角形进行分析研究[3].

4 促进迁移

如果在解题过程中遇到两角和为45°时,往往与等腰直角三角形相联系,或利用角之间和的关系进行等量代换,确定角与角之间的关系.

图7

在这道试题中一个比较明显的条件就是∠FEP+∠G=45°,如何转化这个条件,形成推理条件呢?如图8,根据∠FEP+∠FGO=45°和∠1=∠FGO+∠GOM,可以得到∠GOM=∠FEP;再根据∠GMO=∠PNE=90°,PE=GO,判断得到△GOM≌△PEN(AAS);再得出G,R,P的坐标分别为(-3,12),(3,6),(6,3);过点Q作QK垂直于x轴于点K,则QK=BK;最后利用直线BQ的解析式得出结论.

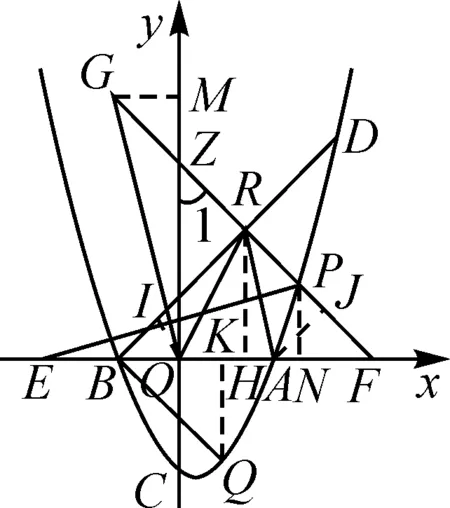
图8

从这几道试题的研究过程可以发现,涉及到“45°”角的问题,通常构造等腰直角三角形,或者和等腰三角形联系起来,借助相关条件形成全等三角形或相似三角形.不管哪种形式,都要准确判断好构造的方向,或者联系内在的隐形等腰三角形,这些都是解题的关键所在[2].

同样地,遇到“60°”角的问题时,可以考虑构造等边三角形,借助等边三角形的特殊性获取更多的条件,以突破问题的疑难点.

综上可以发现,找到一种问题的解决思路,就能通过问题所体现的特点,举一反三,这也是真正把握问题本质的要求所在.在教学中要充分挖掘这类问题的功效,加强问题联想训练,诱发学生解题思维,积极拓宽解题模式训练,同时也要注意增强问题的潜在价值,在训练过程中引导学生不断深入探究,找到问题的模型,为提升综合素养奠定基础.