例谈核心素养视域下的教学整体把握

⦿南京市陶行知学校 罗 尉

《义务教育数学课程标准(2022版)》(下简称新课标)在教学建议中特别提出“教学目标的设定要体现整体性”,“改变过于注重以课时为单位的教学设计,推进单元整体教学设计,体现数学知识之间的内在逻辑关系,以及学习内容与核心素养表现的关联”.基于此,笔者结合“二次函数的图象与性质”教学实际谈谈以单元主题教学来实现教学整体把握的实践与思考.

1 教学分析

1.1 已具备的认知水平和活动经验

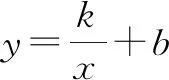
1.2 确定二次函数图象与性质的研究思路

复杂的问题要从最简单的入手,二次函数图象的研究可以从y=ax2开始,对于这类形式的二次函数的图象与性质,可让学生借助已有经验自行研究.接着,大部分学生会自然地去研究y=ax2+k的图象,毕竟已经有了图象上下平移的研究经验.但学生的思路如何能自然地生长到研究y=a(x+h)2的图象上呢?这个时候,学生很容易受一般式y=ax2+bx+c的影响,直接在此基础上加上一次项,从而去研究函数y=ax2+bx或y=ax2+bx+c的图象.这时,不要怕出错,更不要直接要求学生回到预设的研究思路上来.不妨大胆地让学生尝试,在他们发现这样研究比较“麻烦”或者与之前的研究相距甚远时,再引导学生借助经验回头看看,便能发现上下平移研究后,还可以通过左右平移变化来继续研究形如y=a(x+h)2的二次函数的图象,进而研究形如y=a(x+h)2+k的二次函数的图象,思路也就更加顺利、自然.这样学生会对函数图象研究思路的理解更加深刻,以后也可用同样的方法去研究更高次的函数图象.

2 教学片段

2.1 环节一:提出问题,讨论研究方法

问题1上节课我们从实际问题中抽象出了一类函数——二次函数,它丰富了函数家族,你能写出一些具体的二次函数吗?

追问1:你能将这些二次函数进行分类吗?

追问2:你能表达出每种形式的二次函数吗?

追问3:任意二次函数y=ax2+bx+c都能写成y=a(x+h)2+k的形式吗?

设计意图：学生自己归纳出二次函数常见的几种形式,为后面图象与性质的研究做铺垫.

问题2如果我们继续研究,你认为可以研究二次函数的哪些方面?你是怎么想到的?

追问1:为什么我们要研究这些内容?

追问2:怎样研究二次函数的图象与性质?

问题3你打算从哪种形式的二次函数开始研究?为什么?

2.2 环节二:合作学习,研究函数性质

活动一:将学生分成几个学习小组,以小组为单位自主研究二次函数y=ax2的图象和性质.

设计意图：让学生借助已有的活动经验自主探究,进一步积累研究函数图象与性质的经验和方法,掌握绘制二次函数图象的技巧,体会从特殊到一般解决问题的思维方式.展示不同小组画的函数图象(如图1),让学生意识到a决定二次函数图象的开口方向和大小.再借助“几何画板”动态演示,让学生直观地体会a的变化与图象变化的对应关系.

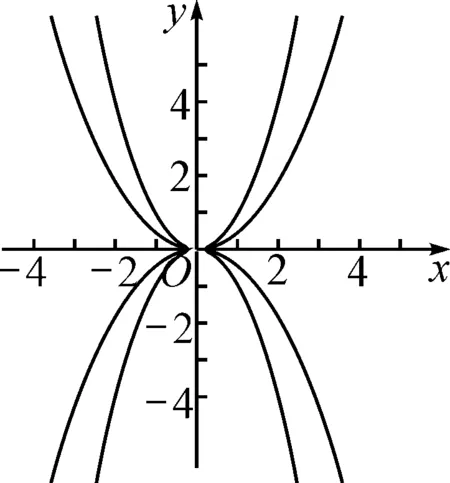
图1

2.3 环节三:共同讨论,明确研究路线

问题4接下来,研究哪种形式的二次函数?

追问1:为什么要这样研究?

追问2:我们以前有过类似的研究吗?

追问3:函数图象左右(上下)平移反映到表达式上是如何变化的?你有什么猜想?

追问4:如果这个猜想正确,那么下一步你打算研究图象的什么平移?以前有这样的研究经验吗?

追问5:是否研究了所有的二次函数的图象特征?

设计意图：借助y=ax2的图象,通过平移,可得出其他形式的二次函数图象,明晰研究二次函数图象的路径(如图2).让学生体会从特殊到一般解决问题的思想方法,结构化分解问题,感受数学思维的力量,体会探究解决问题策略的魅力,理解研究问题先思后做的重要性[2].

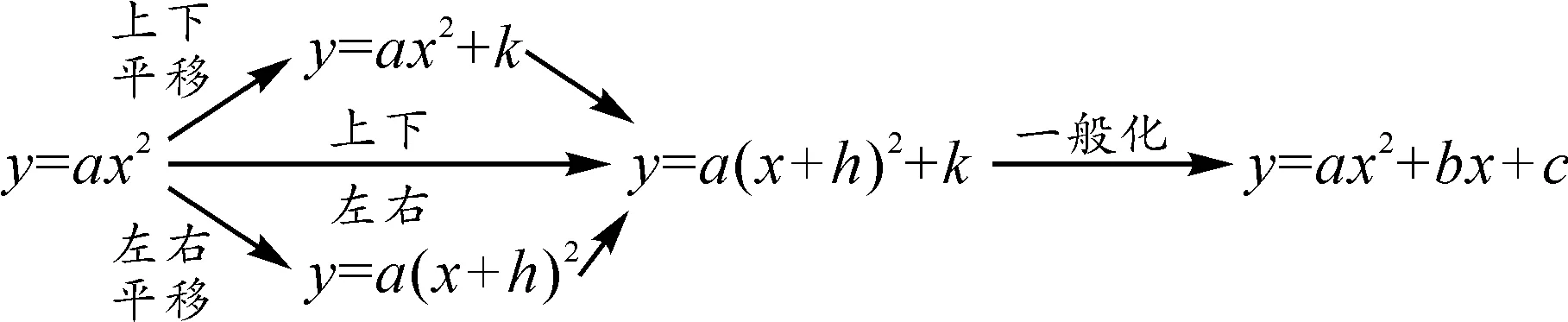
图2

活动二:借助研究y=ax2图象的经验,根据讨论的研究路线,自主研究函数y=ax2+k,y=a(x+h)2以及y=a(x+h)2+k的图象与性质.

设计意图：让学生运用平移法画出函数图象,说出函数的大致性质,教师通过“几何画板”进行验证.在此过程中,可以借助“几何画板”的动画演示,帮助学生理解常量h,k对函数图象位置的影响,明确形如y=a(x+h)2+k的二次函数中常量a,h,k的作用.

问题5你打算如何画y=ax2+bx+c的图象?

设计意图：倒逼学生将一般式y=ax2+bx+c通过配方法转化成y=a(x+h)2+k的形式,借助刚才的研究方法得出其函数图象,让学生感受结构化解决问题的便捷性.当然,还可以采用“列表—描点—连线”这样的通法画函数图象.

若在第一个环节中,学生归纳了二次函数y=a(x+m)(x+n)的形式,这时候可以引导学生先观察函数表达式的结构,借助一元二次方程中因式分解法的学习经验,容易想到点(-m,0)和(-n,0)对应着函数图象与x轴的交点,再借助常量a就可以简单地画出该二次函数的图象.当然,这里处理的程度取决于学生的研究能力.

3 教学反思

3.1 积累数学活动经验,建构知识体系

教材中函数主题的内容被安排在不同的学期,希望通过螺旋上升的方式帮助学生逐步理解函数.因此,在函数的教学中更需要教师以主题单元等形式进行整体把握,逐步推进.通过整体把握教学内容,教师了解本章知识的产生与来源和发展的结构及其相互之间的关联,以及它们具有的价值和意义,建立对所学知识的本质理解,帮助学生结合已有的认知,建构条理分明、互相关联的数学知识体系.

在积累数学活动经验的过程中,体会和感悟不同数学教学内容背后具有一致性、可迁移性的数学思想与解决问题的方法,学会研究一类问题的方法[2].在遇到新问题时,能借助已有的数学活动经验,结构化地分析问题,创造性地解决问题.

3.2 渗透数学思想方法,发展核心素养

数学核心素养的发展具有阶段性、连续性、整合性等特点.教学的整体把握,因其具有整体性的目标设计与规划,所以更有利于学生逐渐形成科学的思维习惯、发展核心素养.函数的教学内容尤其是其中蕴含的数学思想,学生需要在较长的过程中逐步认识与理解.在此过程中,教师可以引导并帮助学生提炼出能打通数学知识之间的关联、发挥核心作用的数学思想方法.

教师在教学中只有关注到教学内容及其相关内容的整体性、逻辑的连贯性、方法的普适性、思想的一致性、思维的系统性[2],才能引领学生亲历研究学习内容的一般过程,并在此过程中建构起有效的认知结构,体会不同研究对象之间研究方法的一致性和可迁移性.这样方可帮助学生逐步理解学习内容的本质,学会用整体的、联系的、发展的眼光看问题,用所学的知识和方法解决问题,形成科学的思维习惯,发展数学核心素养.