促进初中生数学建模素养发展的教学策略研究*

⦿江苏省仪征市新集初级中学 李爱民

数学的思想包括数、形以及数与形结合的推理过程.建模过程是学生综合运用基本数学知识与数学思维去解读生活中问题的成长历程.因此,数学建模与素养发展息息相关,数学建模包括学生数学思维、自主实践能力的培养、数学素养的构建等方面.促进初中生数学建模素养发展的教学策略研究是当下教育教学的需要.

1 搭建数与式的桥梁,激发学生的建模意识

意识是形成思维的前提,思维是形成素养的条件,它们是层层递进、互相依赖的关系.在帮助学生发展数学建模素养时,首先创设学生关注的情境,通过兴趣引导,激发建模意识,并将这种意识贯穿于数学训练中,促使他们逐渐形成数学思维.

数学的思维是抽象的,教学过程中通常采用直观的形式将实际问题转化为抽象的数学问题,这种转化就是帮助学生形成数学思维的过程,是对数学问题的建模.“直观的形式”来源于生活现象,需要学生细致入微、灵活敏锐地观察生活,然后试着以数学的思维去解读生活实际.

例如,讲授苏科版八年级下册“10.5分式方程”的应用时,在课堂解决问题环节创设以下情境.

案例1(2022年江苏省泰州市中考试题)为了改善生态环境,某乡村计划植树4 000棵.由于志愿者的支援,实际工作效率提高了20%,结果比原方案提前3天完成,并且多植树80棵,原计划植树多少天?

分析：方法1——对比观察法.

原方案实际工作完成时间/天t(假设)t-3每天完成量/棵4 000t4 000+80t-3

方法2:

原方案实际工作每天完成量/棵x(假设)(1+20%)x植树总量/棵4 0004 000+80

通过案例1的分析可以发现,培养学生观察生活现象的兴趣和能力,有利于他们在课堂学习过程中自然而然地采用观察法解决问题.案例1中的两种分析,都是以比较观察、量化观察为线索,根据得到的现象进行思考,从而找出隐藏在现象背后的数学实质.

2 细挖教材知识内容,引导数学建模方法

初中生处于直观思维活跃,而抽象思维逐渐形成的阶段.数学是一种抽象化的解决实际问题的工具,掌握数学建模知识,需要将数学建模融入到学生数学学习中,需要教师对现有教材进行深入浅出的挖掘.学科素养的发展,更需要在授课过程中潜移默化地向学生传递建模方法,帮助他们提升数学学习能力,让建模的难度循序渐进、逐步攀升.

如在学习苏科版八年级上册“6.4用一次函数解决问题”时,通过课题组的研究认为,在习题课环节,可以采用例题引导知识建模的方法.

案例2(2022年江苏省南通市中考题改编)定义:如图1,A,B为直线l同侧的两点,过点A作直线l的对称点A′,连接A′B交直线l于点P,连接AP,那么称点P为点A,B关于直线l的“等角点”.

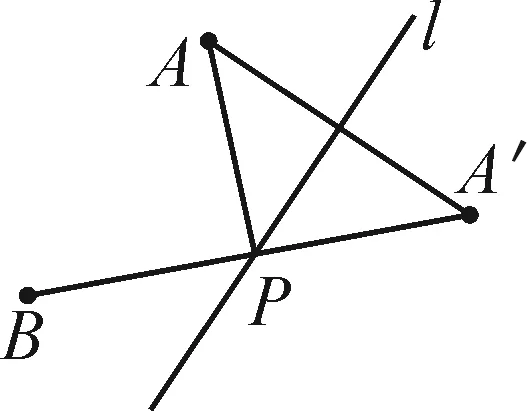
图1

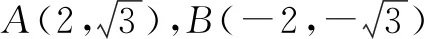
图2

课堂上在深入解读基本数学知识的同时,引导学生从基于数学建模的问题解决方式入手,选取类似知识点以建模方式进行讲解,有利于学生对数学思想的内化.通过课堂典例的引导,加深学生印象,并于适当时机对建模方法加以归纳总结、强化信息的提取、释疑的策划、模型的构建等,让学生在思想的同化过程中发展数学建模素养.

3 思考生活实际问题,促进建模素养发展

将建模思维、方法运用到生活情境中去解决问题,是初中生对数学建模素养发展的深层次目标.在这一过程中,需要从初中生的学情出发,了解他们的学习特点及兴趣,注意选材,将更多有趣的生活案例引入教学之中,并以数学建模的方式进行分析,使学生逐渐感受到用数学建模解疑生活实际的乐趣,进而激发学生自发进行建模活动.

在“不等式”复习课环节,课题组成员提出了引用如下一个案例.

案例3(2022年江苏省南通市中考题)小明购置A,B两种商品,每次购置同一种商品的单价相同,具体信息如下表:

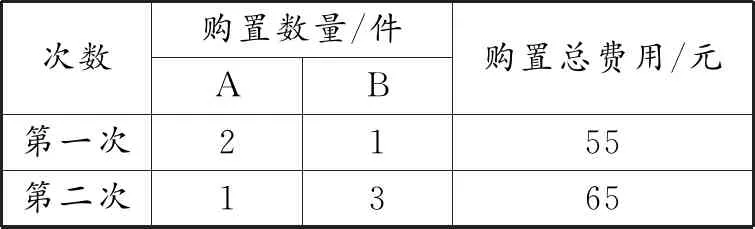
次数购置数量/件AB购置总费用/元第一次2155第二次1365

根据以上信息解答以下问题:

(1)求A,B两种商品的单价;

(2)假设第三次购置这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购置方案,并说明理由.

分析：(1)设A,B两种商品的单价分别为x元和y元,根据题意不难得到二元一次方程2x+y=55和x+3y=65,解得x=20,y=15.

(2)第三次购置这两种商品共12件,若购置A,B种商品分别为a,b件,则a+b=12;A种商品的数量不少于B种商品数量的2倍,即a≥2b.由此可得0≤b≤4.故购置总费用为20a+15b.由20a+15b=20(12-b)+15b=240-5b,得当b=4,a=8时,最省钱.

案例3的问题情境与初中生的实际生活紧密相关,问题(1)属于二元一次方程组的知识应用,也为问题(2)作铺垫;问题(2)是不等式的应用,要解决的问题是设计出最省钱的购置方案,其实是利用不等式求最值.由此可见,中考试题问题设置的难度是逐步上升的,因此,课堂教学中的建模过程也应由浅入深,逐步夯实加固数学学科素养.

在教学中,从学生的实际学情出发,结合学生的数学建模能力合理安排问题梯度,以基础知识带动知识应用.多创设与生活情境相关的问题,多留给学生思考和探究空间,鼓励学生创新出更多的建模思路.

总而言之,促进初中生数学建模素养发展的教学在于搭建数与式的桥梁,即对数与式的关联进行建模,形成数学的基本思想方法;夯实教与学的环节,让数学思维方法在基本的训练过程中得到升华,从而使数学素养得以发展.