大口径X80管道沉管应力响应规律与临界深度分析*

石 彤,王炎兵,金广义,刘啸奔,张 宏,黄启玉

(1. 中国石油大学(北京)油气管道输送安全国家工程实验室/石油工程教育部重点实验室/城市油气输配技术北京市重点实验室 北京 102249;2. 吉林省焓荣科技有限公司 吉林 长春 130033)

0 引 言

“十四五”期间,随着对油气需求量的不断加大,我国大口径高钢级长输管道建设将进入高峰期[1-2]。而作为管道建设重要的一环,下沟铺设的安全性就显得尤为重要。沉管法是利用管道自身重力将管道自然降落到管沟内的施工方法,因为沉管施工具有征地协调量小、操作简便、施工作业效率高等优点,在我国管道建设中得到了越来越多的应用[3-6]。但是,由于沉管施工过程中存在较大的管沟落差,管道发生弯曲变形,容易在局部产生较大的拉压应变,严重时将导致拉裂或屈曲失效。

针对沉管下沟管道铺设方法,国内外学者开展了一系列研究。在沉管施工方法与解析计算研究方面,康万平、刘长江、李艳华等人[7]研究了不同施工环境下管道铺设方法的选择以及沉管下沟在油气长输管道施工中的应用。张英奎等人[8]介绍了西气东输管道工程在水网地区采用大口径管道施工的特点及方法。对施工便道修筑和作业带加固、河流和水塘及道路的穿越、管材运输等进行了论述,为今后类似的管道施工建设积累了一定的经验。季蓓蕾、刘啸奔等人[9]研究了不同沉降形式对管道轴向应力状态的影响,掌握大口径管道的轴向应力应变状态,保障了管道的安全运行。王付会等人[10]将模型简化成超静定梁,最终推导出不同深度管道最大应力公式。夏梦莹、张宏等[11]基于弹性梁理论,给出了挖沟过程中管道挠曲线微分方程,通过边界条件与协调方程,给出了考虑几何非线性的挖沟过程中管道应力与变形解析计算方法。刘啸奔等人[12]提出一种改进的位移变形作用下海底管道应变解析分析方法,根据线性强化模型考虑了管材的非线性本构关系,最终基于平衡方程和迭代计算,可以精确计算管道应力应变。在数值计算方面,程浩力等人[13]对高地下水位段采用单侧沉管下沟的施工工艺进行了有限元模型验证,得到了小口径油气管线在高地下水位段施工的相关结论。孟佳等[14]简化出管道和土体相互作用的物理模型,利用 ANSYS 软件进行沉管下沟的开挖长度分析。谷青悦等人[15]使用有限元模型对管道沉管下沟所受应力进行模拟计算和比较分析,论证该长输管道项目采用管段端部沉管下沟或管段中间沉管下沟的施工方法。刘玉卿等人[16-17]利用有限元方法分析了中俄东线采用沉管下沟施工作业方式的可行性。

综上所述,虽然国内外对沉管施工方法进行了一定的探究,综合采用解析法和有限元方法进行了管道沉管下沟过程中管道过程的仿真分析,但未得到X80管道沉管下沟的临界悬空长度与沉管深度,现场施工缺乏直接指导。针对此,本文基于非线性有限元法,建立我国D1 219 mm X80直管段管道沉管下沟应变数值计算模型,通过分析X80管道在沉管下沟时的变形过程,得到管道完全沉管时悬空长度与管沟深度的关联关系,进而得到完全沉管施工临界的悬空长度与管沟深度。研究成果可以直接指导大口径X80管道管沟开挖过程的控制,保障沉管施工安全、高效进行。

1 沉管下沟简介

1.1 沉管过程简介

沉管下沟指的是沿管道开挖管沟,利用管道自身重力作用缓慢将管道自然下沉到管沟内的施工方法。Q/SY GDJ 0387—2014 《油气输送管道沉管下沟施工规范》中将沉管下沟分为单侧沉管下沟和双侧沉管下沟,其中双侧下沟的方式在工程实际中应用更广泛。

双侧沉管下沟可分为双侧单向沉管下沟及双侧背向沉管下沟。双侧单向沉管下沟是从管段的一端开始,逐步向管段另一端进行管沟开挖和沉管下沟作业,如图1(a)所示;双侧背向沉管下沟则是从管段的中间一点开始,同时向两端进行管沟开挖和沉管下沟作业,如图1(b)所示。当管道完全接触管沟沟底时,视为完全沉管。

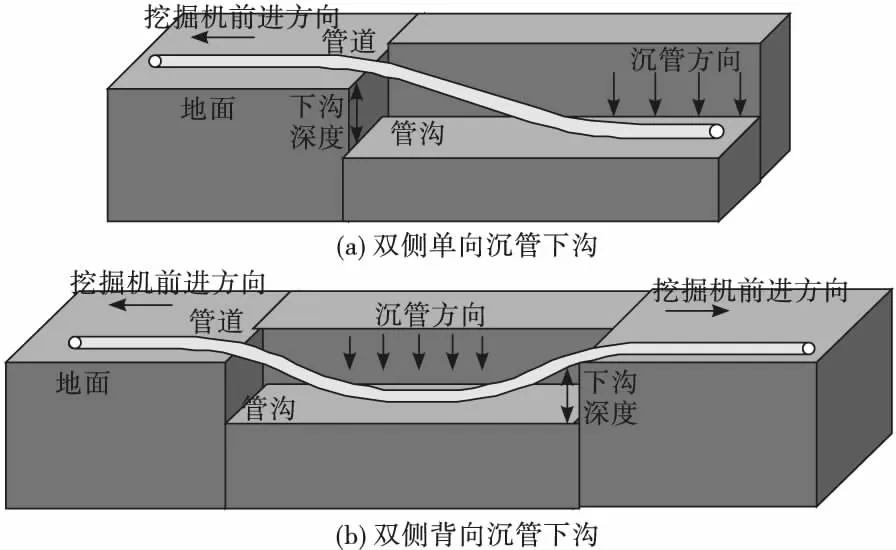
图1 双侧沉管下沟示意图

1.2 沉管施工中管道应力控制要求

沉管过程中因管道会产生较大范围的垂向弯曲,进而形成较大的轴向弯曲应力,根据Q/SY GDJ 0387—2014《油气输送管道沉管下沟施工规范》的规定,我国管道沉管敷设时管道的许用应力应满足:

σe=σh-σa≤[σ]=0.8σs

(1)

式中:σe为管道中的等效应力,MPa;σh为管道环向应力,MPa;σa为管道轴向应力,MPa;[σ]为管道设计的许用应力,MPa;σs为管材的最低屈服强度,MPa。

2 管道沉管下沟有限元模型

应用非线性有限元分析软件,建立D1 219 mm X80直管段管道沉管下沟的数值计算模型,分析X80直管段管道在沉管下沟施工时的变形过程,经计算得到管道完全沉管时悬空长度与应力响应规律,并计算得到临界深度,可直接指导沉管施工管沟开挖并校核油气长输管道沉管下沟的安全性。

下沟过程中,管道长度达数百米,针对管道沉管下沟数值计算模型,将管道本体简化为三维薄壁管,使用有限元软件ABAQUS中的PIPE 31空间线性管单元进行模拟。管道材料采用线弹性,其弹性模量为210 GPa、泊松比0.3,最小屈服强度555 MPa。考虑到下沟管段足够长,管道两端自由约束。在下沟敷设过程中,管道受到重力和土体支撑力的作用,重力载荷即为管道自重,以惯性力的方式施加。

在下沟过程中,在管沟边缘支点处会对管道进行挤压,产生较大应力集中现象,管道最大拉应力出现在管沟边缘管顶处。计算时,基于建立的双侧单向沉管下沟与双侧背向沉管下沟有限元模型,通过将不同位置土块下移模拟挖掘机开挖产生的沟底深度,模拟完全沉管时悬空长度与管顶最大应力。建立的双侧单向沉管下沟与双侧背向沉管下沟有限元模型如图2所示。

图2 双侧沉管下沟有限元模型

3 管道应力和悬空长度影响分析

3.1 不同土壤对管道应力的影响

在进行沉管敷设施工时,不同土壤类型会对沉管敷设时管道应力有一定影响。为探究大口径高钢级长输管道不同土壤情况下双侧单向与背向完全沉管施工时管道悬空长度与管顶最大应力状态分布规律,选取D1 219 mm X80管道,以软黏土、中黏土、硬黏土、松砂、中砂和密砂六种常见的土壤类型及3 m沟深施工工况为例,进行数值仿真计算。依据BS EN 1997-1—2004《欧洲法规7:土木设计总则》中给出的土壤类型,进行土壤参数取值,6种常见土壤类型弹性模量见表1。

表1 不同土壤类型弹性模量 MPa

D1 219 mm管道3 m沉降时管道纵向位移分布曲线如图3所示,双侧单向与双侧背向完全沉管时,管道悬空长度随土壤弹性模量增大而增加,而后趋于稳定,土壤类型为弹性模量较大的密砂时,单向下沟在92.7 m左右,背向下沟在93.5 m左右。计算结果说明在管径不变条件下,土壤参数对沉管施工中管道悬空长度有一定影响,但影响较小。不同土壤参数、同一下沟深度工况管道悬空长度详细计算结果见表2。

表2 D1 219 mm管道不同土壤参数双侧单向、双侧背向沉管下沟悬空长度计算表 m

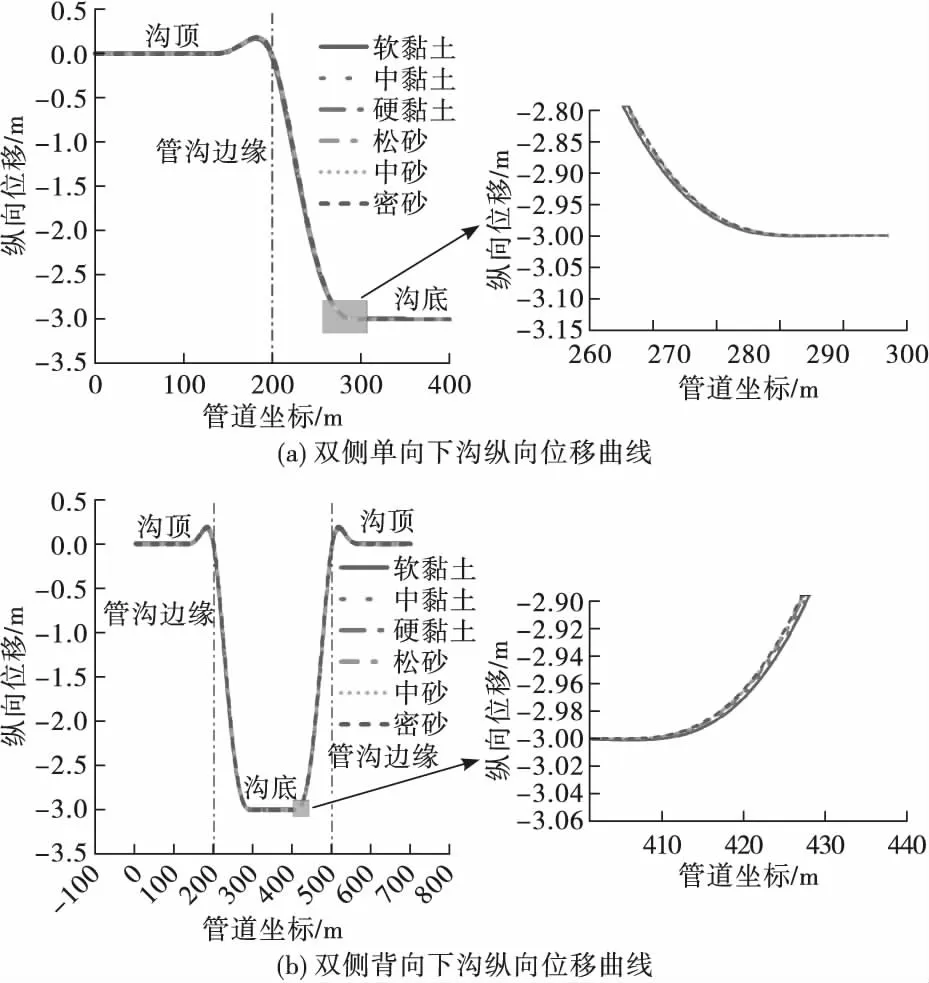
图3 不同土壤管道3 m沉降时双侧单向和双侧背向管道纵向位移曲线

D1 219 mm管道3 m沉降时管顶轴向应力分布曲线如图4所示。

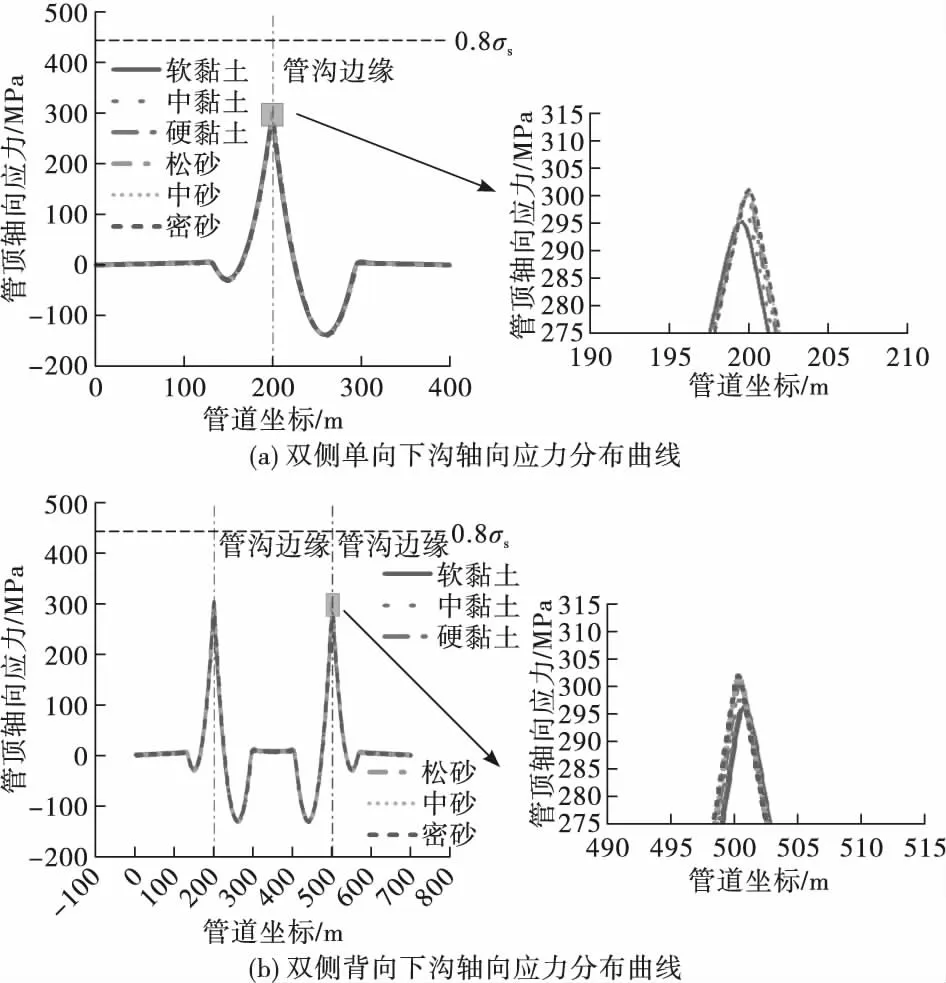
图4 不同土壤管道3m沉降时双侧单向和双侧背向管顶轴向应力分布曲线

双侧单向与双侧背向完全沉管时,管顶最大拉应力位于下沟施工边界处,管顶最大拉应力随着土壤弹性模量增大而趋于稳定。土壤类型为密砂时,双侧单向沉管管道管顶最大应力为301.3 MPa左右,双侧背向沉管管道管顶最大应力为302.2 MPa左右。由计算结果可知,同一直径、壁厚管道,管道双侧单向、双侧背向完全沉管时管顶最大拉应力随土壤弹性模量增大而增加并趋于稳定。不同土壤弹性模量、同一下沟深度工况管顶轴向应力详细计算结果见表3。

表3 D1 219 mm管道不同土壤参数双侧单向、双侧背向沉管下沟管顶最大拉应力计算表 MPa

3.2 管道壁厚对管道应力的影响

为探究大口径高钢级不同壁厚长输管道在双侧单向与背向完全沉管施工时管道悬空长度与管顶最大应力状态分布规律,选取壁厚18.4、22、27.5 mm的3种D1 219 mm X80管道,以密砂、下沟深度3、4、5 m施工工况为例,进行数值仿真计算。

D1 219 mm管道3 m沉降时管道纵向位移分布曲线如图5所示。

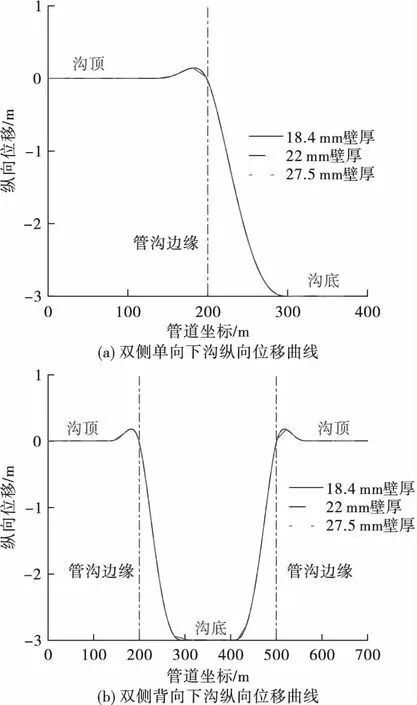
图5 不同壁厚管道3 m沉降时双侧单向和双侧背向管道纵向位移曲线

双侧单向与双侧背向完全沉管时,不同壁厚管道悬空长度基本相当,在92 m左右。说明在管径不变条件下,管道壁厚在沉管施工中对管道悬空长度影响较小,同一管径条件下管道完全沉管时,管沟开挖长度基本一致便满足施工要求。不同壁厚、同一下沟深度工况管道悬空长度详细计算结果见表4。

表4 D1 219 mm管道不同深度双侧单向、双侧背向沉管下沟悬空长度计算表

D1 219 mm管道3 m沉降时的管顶轴向应力分布曲线如图6所示。双侧单向与双侧背向完全沉管时,管顶最大拉应力位于下沟施工边界处。双侧单向沉管时,不同壁厚管道管顶最大应力为301.3 MPa左右。双侧背向沉管时,不同壁厚管道管顶最大应力为302.2 MPa左右。由此可见,同一直径、不同壁厚管道双侧单向、双侧背向完全沉管时管顶最大拉应力基本相当,说明在管径不变条件下,管道壁厚对完全沉管时管顶最大拉应力影响较小。不同壁厚、同一下沟深度工况,管顶轴向应力详细计算结果见表5。

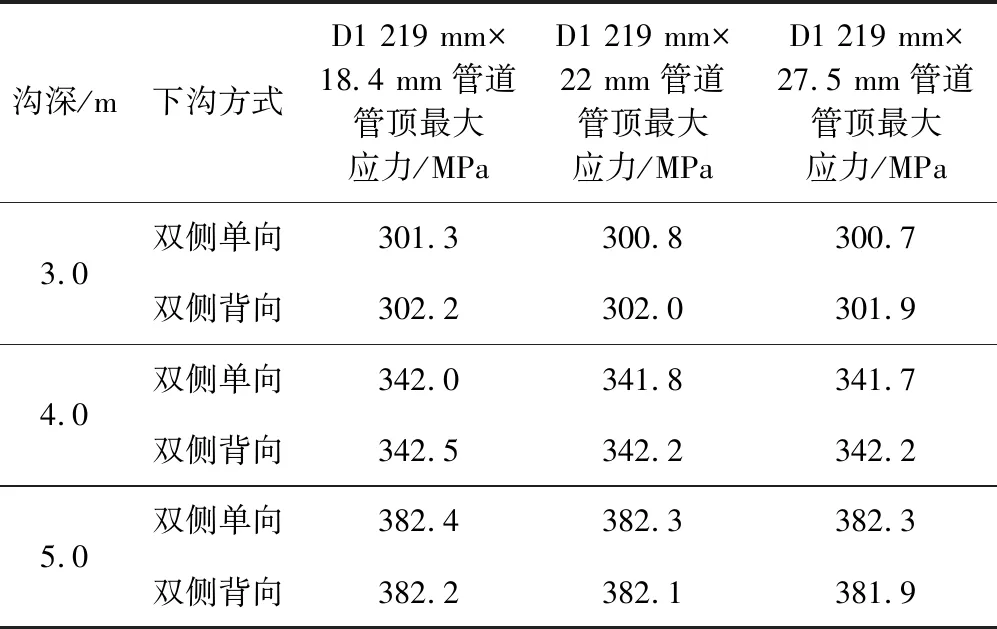
表5 D1 219 mm管道不同深度双侧单向、双侧背向沉管下沟管顶最大拉应力计算表

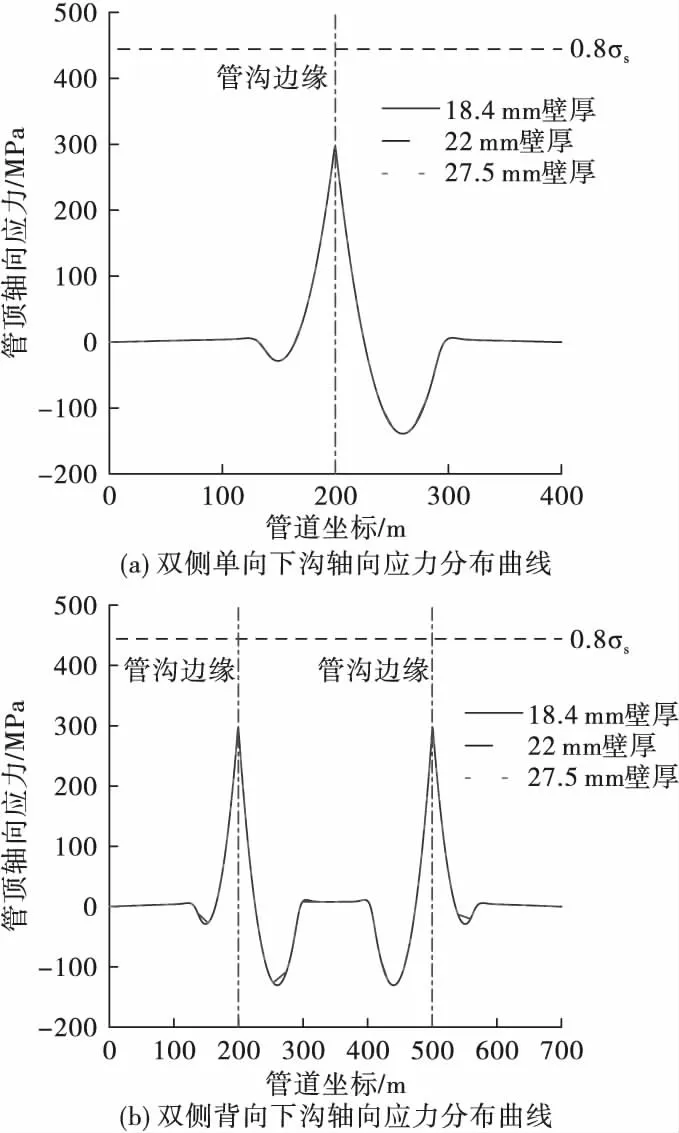
图6 不同壁厚管道3 m沉降时双侧单向和双侧背向管顶轴向应力分布曲线

3.3 支墩位置对管道应力的影响

管道下沟施工时,支墩一般间隔12 m设置,随着管沟开挖,支墩会被人工清除,支墩与管沟的距离在0～12 m之间连续变化。为探究大口径高钢级长输管道在不同支墩位置时,双侧单向与背向完全沉管施工管道悬空长度与管顶最大应力状态分布规律,选取D1 219 mm×18.4 mm X80管道,以密砂、下沟深度3 m、支墩位置距管沟0、4、8、12 m工况为例,进行数值仿真计算。

D1 219 mm×18.4 mm管道不同支墩位置3 m沟深沉降时,管道纵向位移分布曲线如图7所示,双侧单向与双侧背向完全沉管时,管道悬空长度保持不变。双侧单向与双侧背向沉管时,不同支墩位置管道悬空长度相差小于0.5 m。由此可见,不同支墩位置施工时,管道的悬空长度变化很小。不同下沟深度工况管道悬空长度详细计算结果见表6。

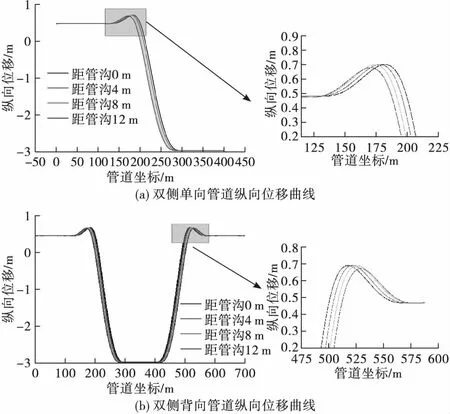
图7 D1 219 mm×18.4 mm管道沟深3 m不同支墩位置双侧单向和双侧背向管道纵向位移曲线

D1 219 mm×18.4 mm管道3 m沉降时,管顶轴向应力分布曲线如图8所示。

图8 D1 219 mm×18.4 mm管道沟深3 m不同支墩位置双侧单向和双侧背向沉管管顶应力曲线

双侧单向与双侧背向完全沉管时,管顶与管底最大应力位置会随着支墩位置的改变而移动,最大应力在320.5 MPa左右。由计算数据可以判断,支墩距管沟位置增加时,管道最大应力值几乎一致,当距离增加到一定值时,管道与管沟边缘接触,土壤给管道一支撑作用,管顶最大应力减小,在距管沟12 m工况下,管顶最大应力为308.4 MPa,因此可以认为支墩位置对管道完全沉管时管顶最大拉应力影响不大。不同支墩位置管顶轴向应力详细计算结果见表7。

表7 D1 219 mm×18.4 mm管道不同支墩位置双侧单向、双侧背向管顶最大拉应力 MPa

3.4 有无支墩对管道应力的影响

为探究大口径高钢级长输管道在有无支墩时双侧单向与背向完全沉管施工管顶最大应力状态与悬空长度分布规律,以不同支墩位置计算结果为基础,选取D1 219 mm×18.4 mm X80管道,以密砂、下沟深度3 m、有无支墩施工工况为例,进行数值仿真计算。

D1 219 mm×18.4 mm管道有无支墩时3 m沉降管道纵向位移曲线如图9所示。双侧单向与双侧背向完全沉管时,有支墩的管道悬空长度要大于无支墩的。由计算结果可知,相同管道尺寸条件下,管道完全沉管时,有支墩情况下需要加长管沟开挖长度。有无支墩时管道悬空长度计算结果见表8。

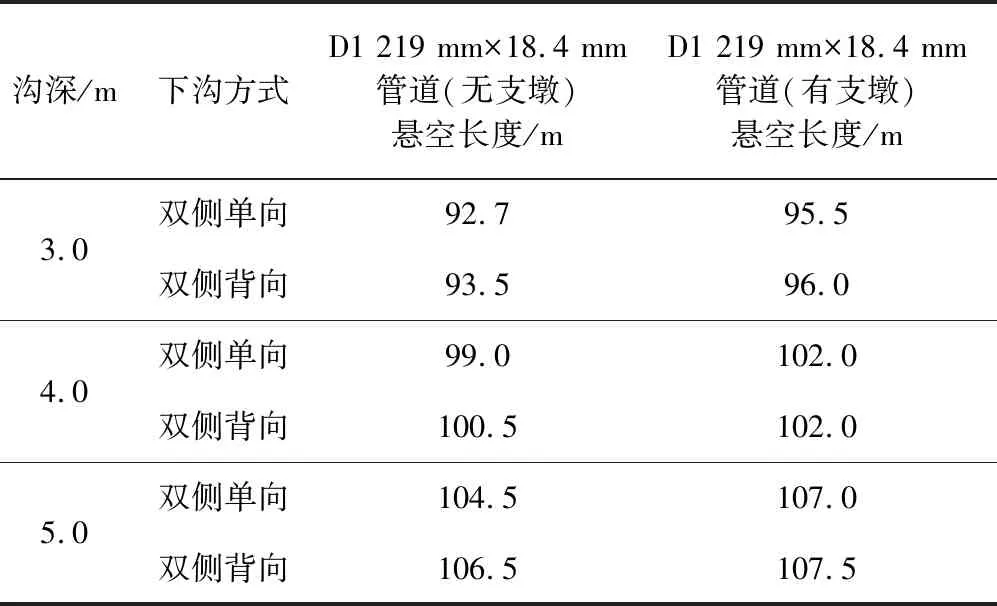
表8 D1 219 mm×18.4 mm管道不同深度有无支墩双侧单向、双侧背向沉管下沟悬空长度

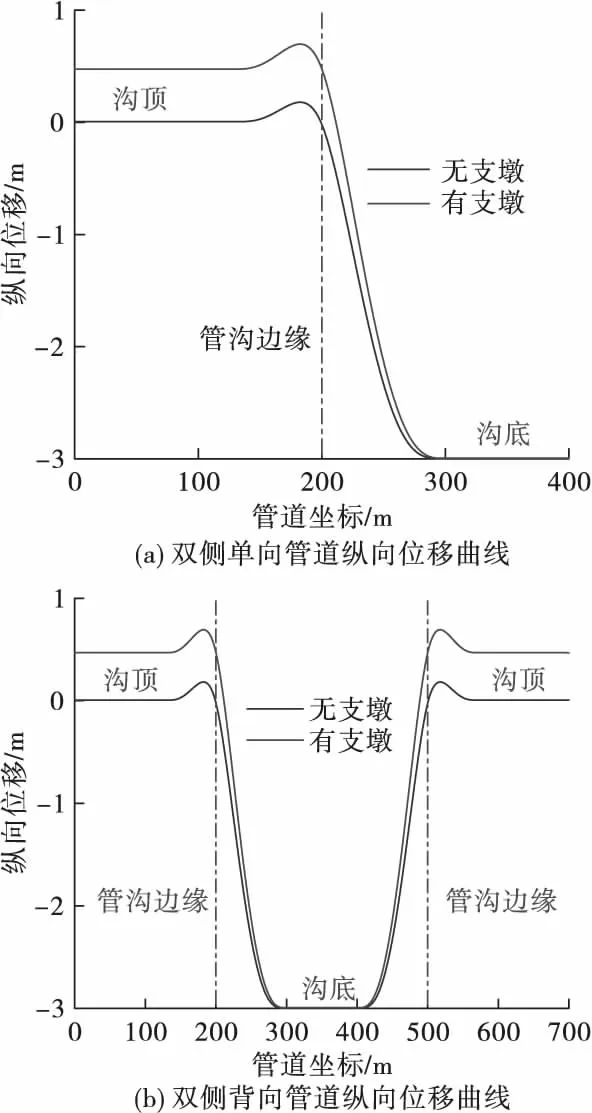
图9 D1 219 mm×18.4 mm管道不同深度有无支墩双侧单向和双侧背向沉管下沟悬空长度计算曲线

D1 219 mm×18.4 mm管道有无支墩时3 m沉降管顶轴向应力分布曲线如图10所示。有支墩工况下管道应力呈波动分布,双侧单向与双侧背向完全沉管时,有支墩的管顶最大拉应力明显要大于无支墩的。由计算结果可知,相同管道尺寸条件下,管道完全沉管时,有支墩情况下管顶最大应力更大。有无支墩时管顶应力详细计算结果见表9。

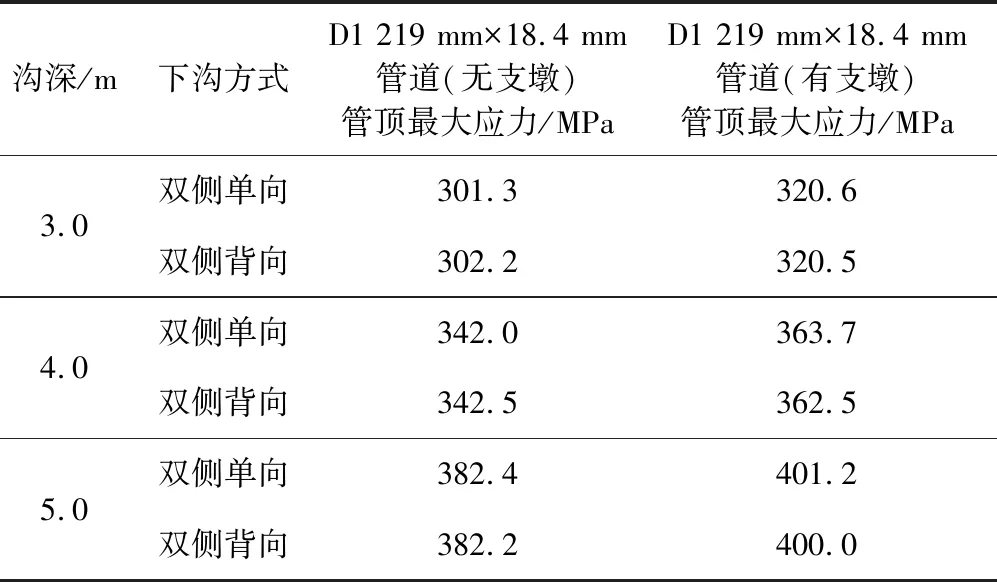
表9 D1 219×18.4 mm管道不同深度有无支墩双侧单向和双侧背向沉管下沟管顶最大拉应力

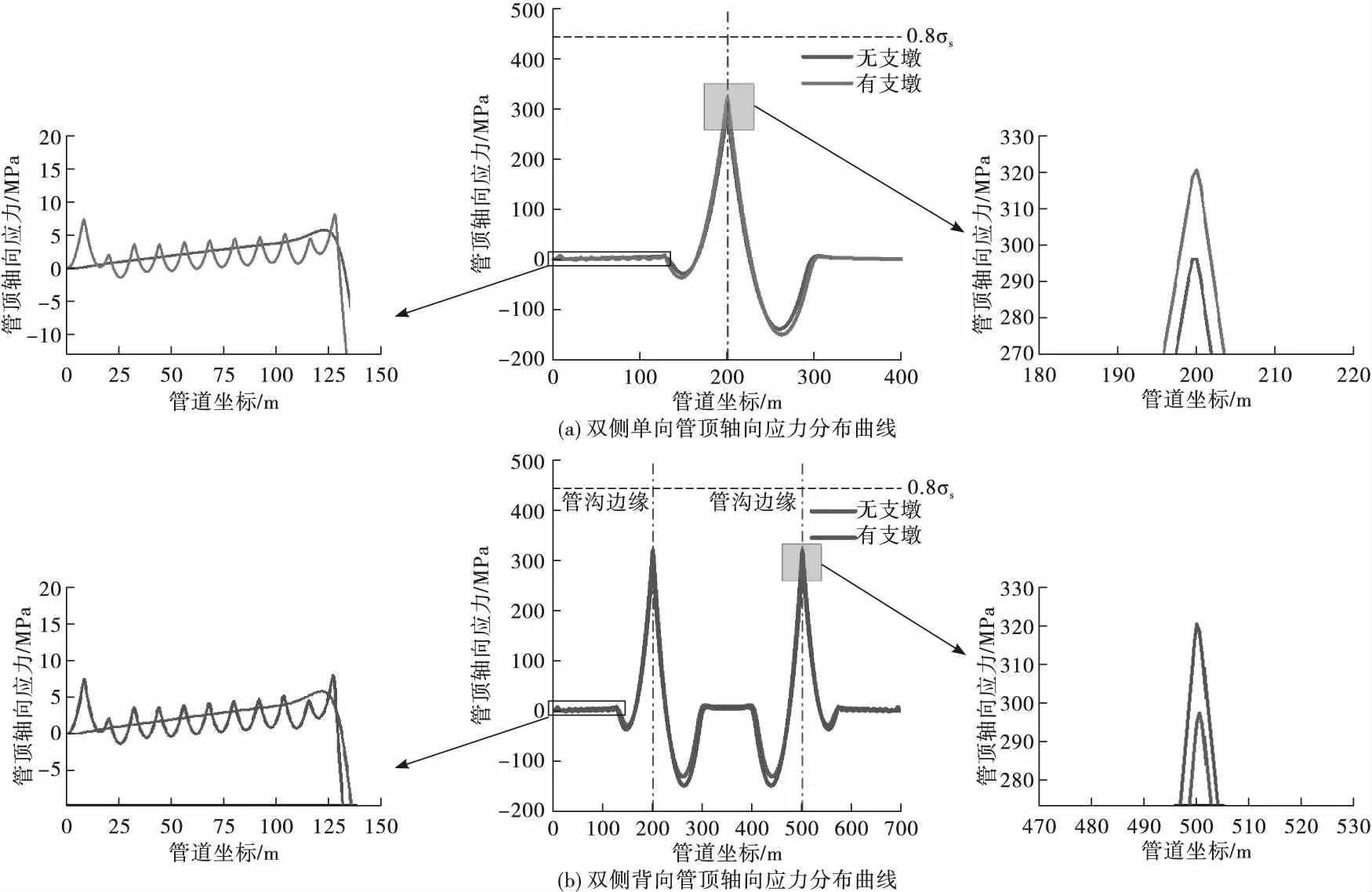
图10 D1 219 mm×18.4 mm管道不同深度有无支墩双侧单向和双侧背向沉管下沟管顶轴向应力分布曲线

3.5 管沟深度对管道应力的影响

基于上述不同土壤、不同壁厚、支墩位置、有无支墩影响因素分析,探究大口径高钢级长输管道在双侧单向与背向不同管沟深度完全沉管施工时管道悬空长度与管顶最大应力状态分布规律,得到管道完全沉管施工临界沟深。选取D1 219 mm×18.4 mm X80管道,并以密砂、不同下沟深度施工工况为例,进行数值仿真计算。

D1 219 mm×18.4 mm管道不同沟深沉降时管道纵向位移分布曲线如图11所示。双侧单向与双侧背向完全沉管时,管道悬空长度随着沟深增加而增大。对于D1 219 mm×18.4 mm管道,下沟深度每增加0.5 m,管道的悬空长度增加值在4 m以下,且随着沟深增加,增幅越来越小。不同下沟深度工况管道悬空长度详细计算结果见表10。

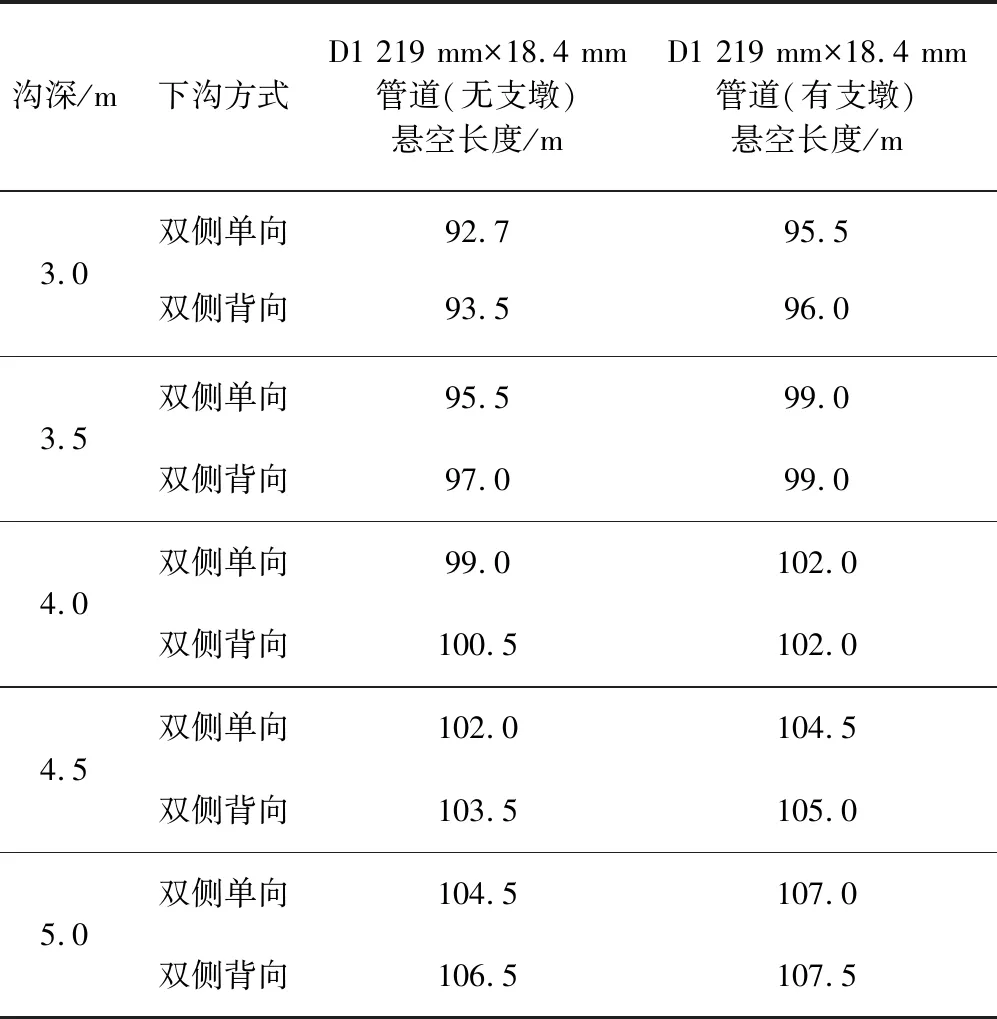
表10 D1 219 mm×18.4 mm管道不同深度双侧单向和双侧背向沉管下沟悬空长度

图11 D1 219 mm×18.4 mm管道不同深度双侧单向和双侧背向沉管下沟悬空长度计算曲线

由D1 219 mm×18.4 mm管道不同沉降时管顶轴向应力分布曲线如图12所示,同一直径、不同沉管深度管道双侧单向、双侧背向完全沉管时管顶轴向应力随着管沟深度增加而增大。可以看出,下沟深度是影响管道安全的最重要因素之一,针对不同尺寸管道的最大下沟深度需经计算得到。对于 D1 219 mm×18.4 mm X80管道,由不同工况管顶应力详细计算结果见表11。

表11 D1 219×18.4 mm管道不同深度双侧单向、双侧背向沉管下沟管顶最大拉应力

图12 D1 219×18.4 mm管道不同深度双侧单向和双侧背向沉管下沟管顶应力曲线

对模型进一步计算临界沟深与悬空长度可知,无支墩情况下,双侧单向沉管沟深达到6.74 m、悬空长度达113.0 m,管道最大应力达到临界许用应力;双侧背向沉管沟深达到6.80 m、悬空长度达115.5 m,管道最大应力达到临界许用应力。有支墩情况下,双侧单向沉管沟深达到6.25 m、悬空长度达113.0 m,管道所受最大应力达到临界许用应力;双侧背向沉管沟深达到6.31 m时,悬空长度达到113.5 m,管道所受最大应力达到临界许用应力。

4 结 论

针对大口径X80直管段管道沉管下沟敷设问题,本文以D1 219 mm X80管道为例,建立了直管段管道沉管下沟敷设参数化数值计算模型,计算了工程中4类影响因素作用下的管道管顶最大拉应力变化及管道纵向位移分布,可以为D1 219 mm X80管道沉管施工提供指导。

1)不同土壤类型条件下,双侧单向与双侧背向完全沉管时,管顶应力和管道悬空长度随土壤弹性模量增大而有小幅增加,并趋于稳定。说明在其他条件不变的情况下,土壤类型对沉管施工中管道悬空长度有一定影响,但这种影响较小。

2)不同管道壁厚条件下,管道应力和悬空长度的变化趋势相同,同一直径、不同壁厚管道双侧单向、双侧背向完全沉管时悬空长度与管顶最大拉应力基本相当,同一管径、不同壁厚条件下,管道完全沉管时管沟开挖长度一致便满足施工要求。

3)不同支墩位置条件下,当支墩位置发生改变时,管顶最大应力位置随支墩位置移动,管道悬空长度与管顶应力基本一致,认为支墩位置对管道施工影响较小。

4)无支墩和有支墩情况下,悬空长度和管顶应力的变化趋势相同,无支墩情况下呈连续性变化,有支墩情况下呈阶梯状或波动状变化;相同管沟深度沉管,管道中最大应力在有支墩情况下大于无支墩情况。

5)同一直径、不同壁厚管道双侧下沟完全沉管时,管顶最大轴向应力随管沟深度增加而增大。对于D1 219 mm X80管道,无支墩情况下,双侧单向与双侧背向沉管临界深度分别为6.74 m和6.80 m;有支墩情况下,双侧单向与双侧背向沉管临界深度分别为6.25 m和6.31 m。