基于集成学习及电阻层析成像的两相流流型辨识

张立峰, 肖 凯

(华北电力大学 自动化系,河北保定 071003)

随着我国工业不断发展,对两相流监测日趋重要。两相流系统在电力、化工和石油等工业部门广泛存在。两相流根据构成系统的相态分为气液两相流、液液两相流、液固两相流和气固两相流等。气液两相流是各类两相流中最常见、最复杂的两相流动体系之一,气液两相流作为一种非平稳过程,其状态的变化具有时变性、非线性和随机性等复杂流动过程的特点,这些因素导致对气液两相流的状态检测十分困难[1-2]。流型是气液两相流最基本的特征参数,因此其他参数的准确测量需要依赖于对流型的了解,对两相流流型的准确辨识具有重要意义[3]。

电阻层析成像(Electrical Resistance Tomography,ERT)是一种用于连续流动相为导电介质的两相流可视化检测方法,其原理为根据不同介质的电导率特性,通过测量敏感场边界信号,反推内部电导率分布图像,从而得到介质分布状况[4],其具有非侵入、结构简单及实时性高等特点[5]。

基于ERT的流型辨识方法可分为2类。一类是基于ERT重建图像进行流型辨识:仝卫国等[6]提出一种基于Landweber迭代图像重建算法和卷积神经网络相结合的流型辨识方法,该方法先利用电容层析成像技术对管道内的气液两相流进行图像重建,然后建立卷积神经网络模型,对重建后的流型图片进行分类,从而达到流型辨识的目的;翁润滢等[7]采用压差传感器对不同流型的压差信号进行采集,在时频分析后将其转换为时频谱图,然后采用卷积神经网络对时频谱图进行分类从而实现流型辨识。另一类则是利用ERT系统测量值,基于信号分析或特征提取结合某种分类方法进行辨识[8]:李凯锋等[9]利用主成分分析法提取ERT测量数据,再通过K-均值聚类算法对泡状流、层状流和环状流实现流型辨识,并验证了该方法的可行性;陈德运等[10]采用主成分分析法对ERT系统中的边界测量电压数据进行特征提取,然后作为支持向量机的输入,对油水两相流的均匀流、层流、环状流和核心流4种流型进行流型辨识,并通过实验验证了该方法的有效性。

在之前的研究中,鲜有人将集成学习与流型辨识相结合,这种方法属于机器学习中的一种,通过构建并结合多个学习器来完成学习任务[11],主要包含Boosting、Bagging及Stacking 3类算法,一般结构是先产生一组“个体学习器”,再用某种策略将它们结合起来[12],所用的策略主要有平均法、投票法和学习法3种。

极限梯度提升(eXtreme Gradient Boosting,XGBoost)是Boosting算法中的一种,由Chen等[13]于2016年提出,该算法在传统GBDT(Gradient Boosting Decision Tree)算法上进行改进[14],基本思想是将多棵分类回归树(Classification And Regression Tree,CART)作为弱分类器,最终组合为一个强分类器,达到提升算法准确率的效果 。

AdaBoost算法也属于Boosting算法中的一种。 其原理是根据前一个弱分类器的分类结果,调整下一个弱分类器的样本权重和弱分类器权重,最后将多个弱分类器组合成一个强分类器,达到提高分类效果的目的[15]。由于AdaBoost算法可以使用不同的分类算法作为弱分类器,并且可以有效地提高算法效果,因此在各种研究中得到了广泛的应用。

笔者先对实验采集的泡状流、弹状流、段塞流和混状流4种流型数据进行帧数均值化,然后利用XGBoost算法进行预训练,并以增益值作为指标对特征进行选择,保留重要特征,去除冗余特征,以此来降低分类模型的复杂度和提高实时性。最后将5个深度神经网络(Deep Neural Networks,DNN)模型作为弱分类器,通过AdaBoost算法组成DNN-AdaBoost强分类器,输入预处理好的数据进行流型辨识,并与其他算法进行比较,以验证DNN-AdaBoost算法在流型辨识中的有效性。

1 电阻层析成像系统原理

电阻层析成像系统由ERT传感器、数据采集系统及重建图像计算机3部分构成[16],见图1。

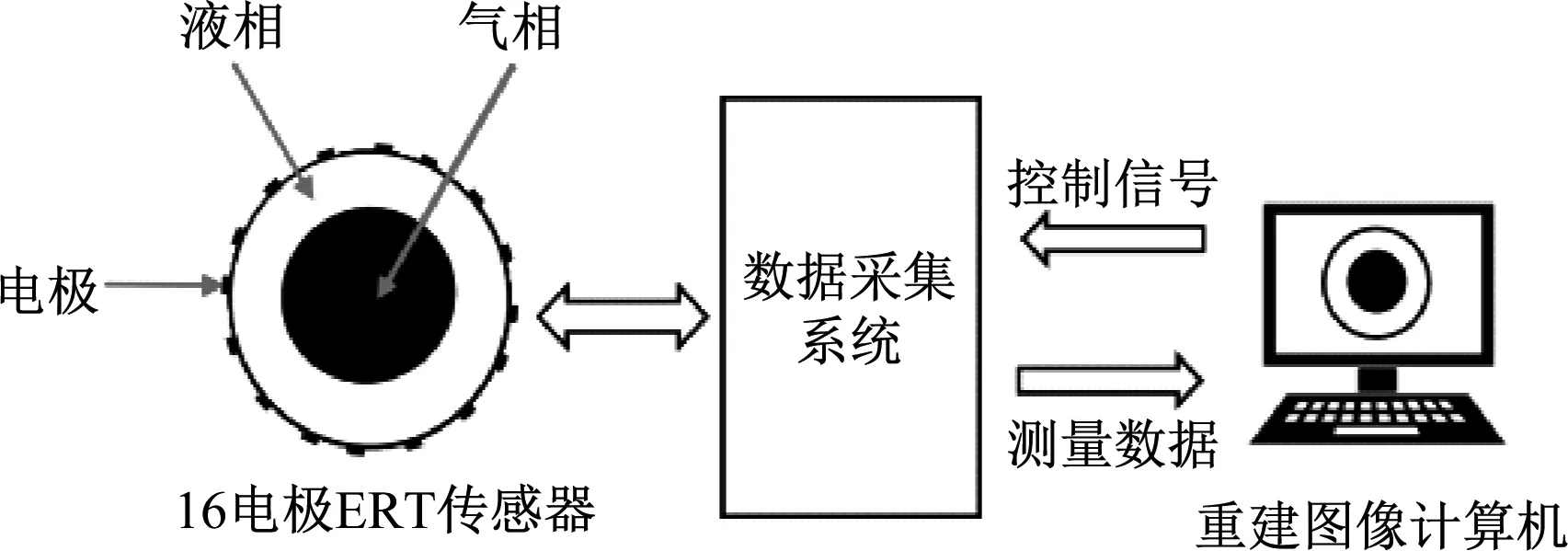
图1 电阻层析成像系统原理图

电阻层析成像系统工作原理是由重建图像计算机对数据采集系统发出控制信号,控制ERT传感器的激励模式及测量模式,并采集测量值。16电极ERT传感器采用相邻激励模式并进行相邻电极电压测量,共采集120个独立边界电压测量值,经A/D转换传回计算机,采用图像重建算法即可获得管道截面电导率分布的重建图像[17]。

2 流型辨识模型

2.1 CART算法

CART算法采用一种二分递归分割的技术,将当前的样本集分为2个子样本集,使得生成的每个非叶子节点都有2个分支。因此,CART算法生成的决策树是结构简洁的二叉树[18]。

CART算法主要分为2步:第一步是将训练样本进行递归地划分自变量空间并进行建树,第二步是用验证数据进行剪枝。建树过程中引入基尼系数H(p),据此选择最优特征,并决定该特征的最优二值切分点,其计算公式如下:

(1)

式中:a为当前类别;A为总类别数;pa为样本点属于第a类的概率。

具有最小基尼系数的属性及其属性值为最优。基尼系数值越小,说明二分之后的子样本的“纯净度”越高,选择该属性作为分裂属性的效果越好,以此完成建树过程。为有效降低过拟合问题,提高模型的泛化能力,需对树模型进行剪枝处理。经过建树以及剪枝处理后即可生成一个CART模型,再将CART模型作为XGBoost算法的弱分类器,最终将多个CART弱分类器结合起来构成一个强分类器,形成XGBoost算法。

2.2 XGBoost算法

XGBoost算法是在GBDT算法上改进而来的,相比于传统的GBDT算法,XGBoost算法无论是在模型精度还是在模型计算速度方面均得到较大改善。其基本思想是将多个CART模型组合,通过前一模型的预测结果来减少后一个模型的偏差,从而提高预测性能[19]。

XGBoost算法最终的强分类器数学模型如下:

(2)

模型的目标优化函数S为:

(3)

(4)

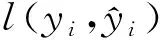
再对损失函数进行二阶泰勒展开,将式(4)代入式(3)得到近似优化目标函数:

(5)

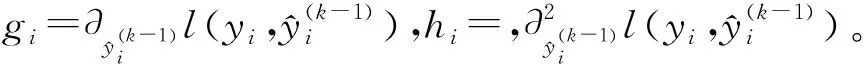
利用XGBoost算法进行预训练,根据预训练的结果可以计算特征的重要性程度,根据特征重要性进行排序后再进行特征选择,以此来达到数据降维的目的。

2.3 DNN神经网络

本文构建的DNN弱分类器模型分为输入层、隐藏层和输出层3部分。隐藏层有 4 层,每层包含 500个神经元节点。ReLU激活函数R(x)用于去线性化,以交叉熵作为损失函数,反向传播用于学习训练调整和更新神经元之间的权重。R(x)表达式为:

(6)

交叉熵损失函数L为:

(7)

式中:N为样本个数;M为类别个数;yic为符号函数,如果第i个样本的真实类别为c,则值为1,否则为0;pic为样本i属于c类的概率。

DNN神经网络的框架图如图2所示。

图2 DNN网络框架图

2.4 DNN-AdaBoost算法

本文构建的DNN-AdaBoost算法模型使用5个DNN模型作为AdaBoost算法的弱分类器,原理是依次训练多个DNN模型,根据上一个DNN分类器的结果调整下一个DNN分类器的样本权重,从而达到自适应提升的效果,最后根据每个DNN分类器分类效果确定其在最终强分类器中的权重[20]。其算法过程如下:

(1) 输入训练样本。

(2) 初始化权值分布Di。

Di=(w1,w2,…,wN)

(8)

式中:wi为第i个样本的权值,每个样本赋予相同的初始权值,为1/N。

(3) 训练弱分类器,共进行TN次迭代,TN为弱分类器的总数。

选择一个DNN神经网络,作为第t个弱分类器Ht并计算该弱分类器在权值分布Dt上的分类误差et:

(9)

式中:wt(i)为第t次迭代中第i个被错误分类样本的权值。

计算当前DNN神经网络在最终强分类器中的权重αt:

(10)

更新下一次迭代的样本权值Dt+1:

(11)

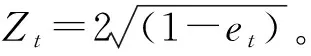
(4) 将各个DNN神经网络弱分类器Ht及其权重αt组合为一个强分类器Hfinal。

(12)

通过符号函数sign的作用,得到最终的强分类器:

(13)

(5) 将测试样本输入强分类器,输出分类结果。

基于集成学习的流型辨识模型框图见图3。

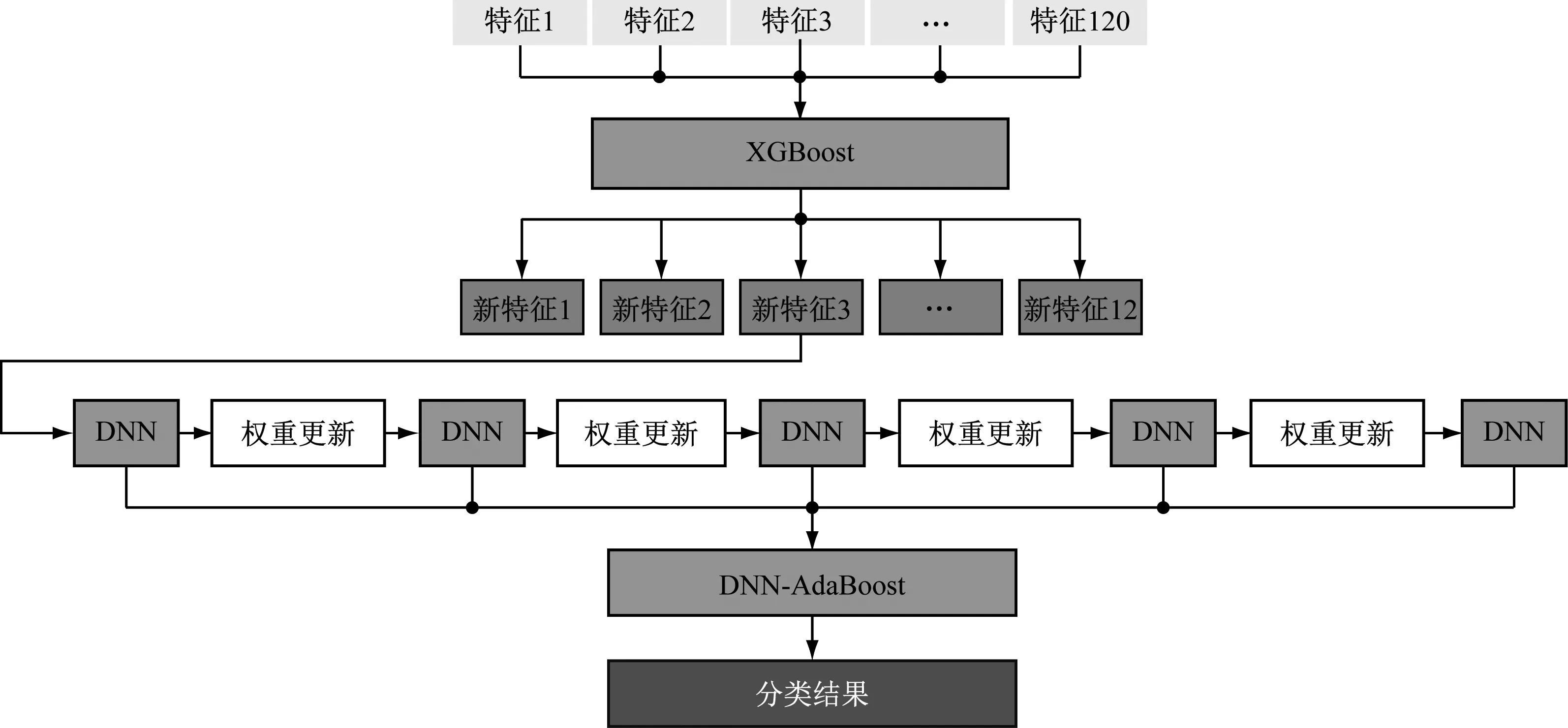
图3 基于集成学习的流型辨识模型框图

3 实验过程及结果分析

3.1 数据采集

使用华北电力大学先进测量实验室的可移动气水两相流实验装置进行实验数据采集,实验装置实物图和示意图分别如图4和图5所示。

图4 实验装置实物图

图5 实验装置示意图

此装置主要由水路循环、气路循环及电阻层析成像三部分组成。首先由空气压缩机压入储气罐里的气体经过压力表、气体涡轮流量计、浮子流量计到达ERT传感器。同时水箱里的水由水泵抽取经过电磁流量计、阀门到达ERT传感器与气体混合形成气液两相流。在水流量不变的情况下,通过调节气相路的阀门开度来改变气量,可以得到不同的气液两相流流型。最后由ERT传感器采集不同流型的信息。参考垂直管道气液两相流的Taitel流型图进行气相及液相的流量配比,当水与气的比例在一定的范围内时,即可得到一种典型流型,同时亦可观察有机玻璃透明管段记录当前流型,得到不同的气液两相流流型。

ERT传感器部分透明直管段的管径为50 mm,其周围安装16电极ERT阵列传感器,采用四电极激励测量策略,采样频率为120 Hz,共可获得120个独立测量值,通过数字化ERT系统将模拟信号转化为数字信号保存至计算机。实验中将水相体积流量固定为1.7 m3/h,通过阀门调节气相流量的大小,进而改变气液两相流的流型状态。经实验观察,选取气相体积流量为0.3 m3/h、0.5 m3/h、1.2 m3/h和2.5 m3/h,分别对应泡状流、弹状流、段塞流及混状流4种流型,如图6所示。

(a) 泡状流

3.2 数据预处理

在实验采集的样本预处理方面,由于每帧数据只包含了极短时间内气液两相流的流型信息,并不能很好地表征其在时间序列下整体流型的流动特征。因此,进行了帧数均值化处理。不同帧数均值化的平均辨识准确率如图7所示。

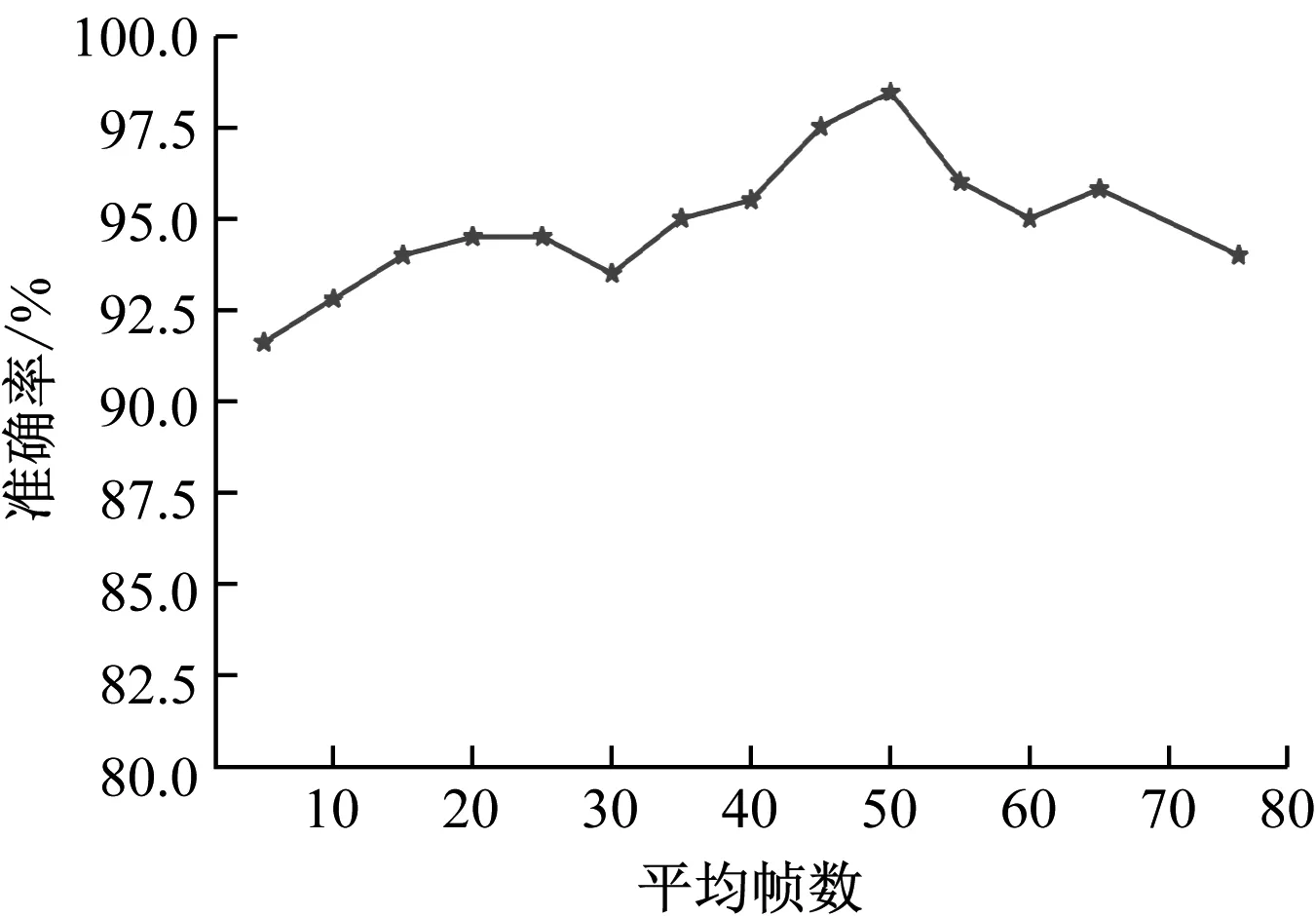
图7 平均辨识准确率

由图7可以看出,对5帧至50帧均值化处理后的流型辨识准确率总体呈逐渐升高的趋势,但继续增加均值化的帧数,又会导致准确率下降,其原因为均值化处理后的数据综合考虑了多个截面的平均信息,极大地降低了用单一截面信息评估整体的局限性,增加了动态流型的整体特征,但过多帧数的均值化又会导致各个流型之间的特征差异变小,从而出现各个流型之间易于混淆的结果。因此,本文选择以每50帧数据均值化的方式对数据进行预处理。

由于采集的数据特征维度为120维,为有效降低模型复杂程度及提高实时性,需对数据进行降维处理。先用XGBoost算法对数据进行预训练,得到每个特征的重要性,然后设置阈值进行特征选取。特征重要性根据gain值β进行评价,其计算公式如下:

(14)

根据式(14)计算每个特征的gain值,如图8所示。由图8可以看出,120个特征所对应的gain值各不相同,即特征重要性不同,综合考虑对算法实时性的要求和精度要求,按照特征重要性进行排序,并设置特征选择的阈值为0.02,据此对特征进行选择,最终选出12个特征组成新的数据特征。为了对比特征选择前后对流型辨识效果的影响,对比了特征选择前后的训练时间、预测时间及4种流型平均辨识准确率,如表1所示。

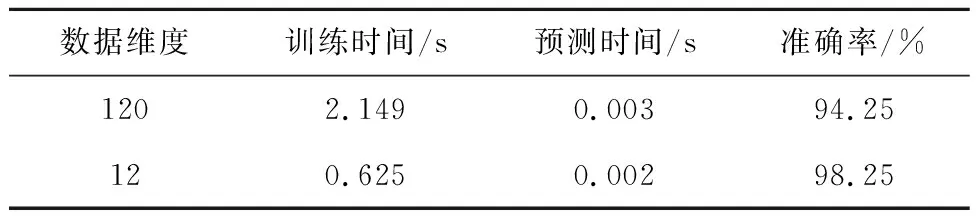
表1 特征选择前后各参数的对比

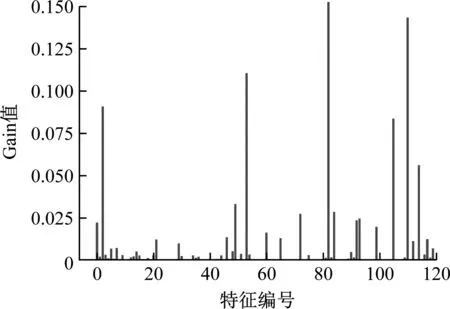
图8 特征重要性

由表1可以看出,在将特征为120维的数据降维到12维后,其训练时间从2.149 s减至0.625 s,预测时间从0.003 s减至0.002 s,准确率从94.25%提高到98.25%,其原因为通过特征选择实现降维,保留了重要特征,去除冗余特征,从而降低了模型复杂程度,提高了算法实时性,并且冗余特征的去除有效降低了过拟合对算法精度的影响,因此算法的实时性和精度均得到了提高。

3.3 流型辨识及结果分析

数据预处理完成后的数据样本共有800个,每个样本维度为12维,将其以4∶1的分布随机划分出640个训练样本及160个测试样本。然后将其输入DNN-AdaBoost算法中进行流型辨识。

DNN-AdaBoost算法中有一些参数(见表2)对模型的整体性能有重要影响。 因此,本文使用网格搜索算法对 DNN-AdaBoost 算法中的参数进行优化。

表2 超参数调优

为了验证AdaBoost算法的提升效果,对比了单独采用DNN算法进行流型辨识与采用自适应提升后的DNN算法(即DNN-AdaBoost算法)对同一批数据的分类效果,结果如图9所示,其中a～d分别对应泡状流、弹状流、段塞流及混状流。

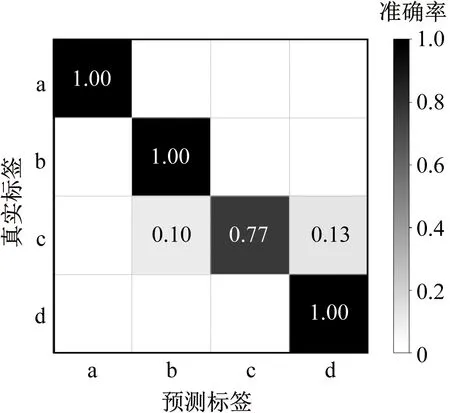
(a) DNN算法

由图9可以看出,DNN模型对4种流型的平均辨识准确率为94.25%,对段塞流的辨识准确率最差,仅为77%,其中10%的样本被错分为弹状流,13%的样本被错分为混状流。 DNN-AdaBoost算法的平均辨识准确率达到98.25%,其中有2%的弹状流样本被错分为段塞流,而段塞流的样本中有3%的样本被错分为弹状流,3%的样本被错分为混状流。2种算法对段塞流流型的辨识效果较差,其原因为段塞流是弹状流至混状流的过渡流型,其流型特征与弹状流、段塞流比较相似,因此易被错分为这两种流型。从2种算法的平均辨识准确率可知,相比DNN算法,由DNN和AdaBoost组成的DNN-AdaBoost算法的辨识精度有所提升,其辨识精度由94.25%提高到98.25%。

为了比较DNN-AdaBoost算法与其他算法的流型辨识精度,使用相同数据输入BP神经网络、SVM、决策树及GBDT算法模型进行流型辨识。由表3可以看出,DNN-AdaBoost 算法模型对泡状流、弹状流、段塞流和混状流的辨识精度均优于BP神经网络、SVM、决策树、GBDT算法和DNN算法模型,其对泡状流、混状流的辨识准确率可达到100%,平均辨识精度可达98.25%。

4 结 论

(1) 流型辨识前对数据进行预处理十分必要。选择不同帧数均值化处理对辨识结果的准确性有较大影响。 经过XGBoost算法特征选择后,可以提高算法的实时性和准确性。

(2) AdaBoost算法对DNN模型的提升效果较为明显,对4种流型的平均辨识准确率从94.25%提高到98.25%。

(3) 经过XGBoost算法特征选择后的DNN-AdaBoost算法对流型辨识的准确率高于BP神经网络、SVM、决策树、GBDT算法和DNN算法,该算法的平均辨识准确率可以达到98.25%。

(4) 所采用的DNN-AdaBoost算法在流型辨识方面取得了较好的效果,但也存在一定的局限性。首先,该算法弱分类器的数目不易确定,需花费较长时间进行寻优;其次,由于组合了多个DNN弱分类器,在数据训练时需耗费较长时间。因此,采用更高效的参数寻优方法及进行模型优化以减少训练时间是后续需要解决的问题。