动态高阶矩风险稳健性测度与参数化组合投资决策研究

刘书婷, 许启发,2, 蒋翠侠

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.过程优化与智能决策教育部重点实验室,安徽 合肥 230009)

0 引言

金融理论与实践表明,金融资产收益往往并非服从正态分布,而是具有非对称以及尖峰肥尾等典型特征。一方面,收益序列分布的左尾通常比右尾长,存在负偏度,意味着收益下降的可能性高于收益上升的可能性;另一方面,收益序列分布比正态分布更加陡峭,存在超额峰度,使得黑天鹅事件发生的可能性极大增加。因此,仅从收益序列前二阶矩出发,难以全面准确刻画金融资产收益行为特征,需要研究其更高阶矩(偏度与峰度)行为。

在偏度(Skewness)与峰度(Kurtosis)的测度中,如传统的矩(分别对应三阶标准矩和四阶标准矩)测度方法,其数值被放大到三次幂和四次幂,很容易受到异常值影响。为此,高阶矩风险的稳健性测度受到学者们的重视。例如, GROENEVELD和MEEDEN[1]提出基于分位数的偏度测度方法; HOGG[2]设计基于分位数的峰度测度方法;KIM和WHITE[3]通过蒙特卡洛实验和实证研究,证明了基于分位数的高阶矩风险测度方法具有稳健性及有效性。为进一步考虑动态高阶矩风险,GHYSELS等[4]构建混频数据分位数回归(MIDAS-QR)模型并用于估计条件分位数,给出了具有时变特征的偏度风险测度方法。然而,关于时变峰度风险的稳健测度方法有待进一步研究。

MARKOWITZ[5]提出均值-方差(M-V)模型,考虑了金融资产收益分布的前二阶矩,在代表收益的均值与代表风险的方差之间进行权衡,取得了巨大成功。随着新的风险测度引入,M-V模型获得了进一步发展。 BRIEC等[6]创造性提出均值-方差-偏度(M-V-S)模型,讨论了带有前三阶矩的组合投资选择。在此框架下,带有偏度风险的组合投资研究不断涌现[7]。随着金融理论与实践的深化以及金融计量建模技术的发展,四阶矩(峰度)风险也受到了越来越多投资者和学者们的关注。在组合投资选择中,理性投资者有意降低峰度风险,以最大程度地减少极端事件发生的可能性。为此, JONDEAU和ROCKINGER[8]利用期望效用函数的泰勒级数展开,将峰度风险引入组合投资模型,建立了均值-方差-偏度-峰度(M-V-S-K)分析框架。在这一框架下,MEHLAWAT等[9]讨论了带有峰度风险的组合投资问题,强调了峰度风险对金融投资决策的显著影响。

实际上,求解带有高阶矩的组合投资模型是一项具有挑战性的工作,已有学者对相关技术进行了探讨。CHEN等[10]等将高阶矩作为目标函数引入到组合投资模型中,其求解被转化为收益、偏度最大化和方差、峰度最小化的非凸规划问题。该方法虽然能够体现投资者追求收益、规避风险的理念,但模型求解存在较大的困难。不同于以收益各阶矩作为目标函数的优化方法,BRANDT等[11]运用参数化组合投资策略,通过最大化投资者期望效用函数求解组合投资模型。这一方法仅需估计较少的参数,显著提高了计算效率。然而,现有关于参数化组合投资的研究仅对收益的前三阶矩进行了讨论,尚未引入峰度风险并考虑对投资者组合投资选择的影响。

鉴于以上,本文研究动态高阶矩风险稳健性测度并建立相关的参数化组合投资决策模型,具体创新性研究工作如下。第一,基于MIDAS-QR模型给出动态峰度风险稳健测度方法,不仅考虑金融市场中峰度风险的时变特征,而且充分利用高频数据信息,提高峰度风险测度的及时性、准确性以及稳健性。第二,使用参数化组合投资策略,将动态偏度风险和动态峰度风险引入组合投资权重函数,联合常绝对风险厌恶(CARA)效用函数,构建动态高阶矩参数化组合投资决策模型,记为B-S-K模型。该模型大幅缩减了待估计参数的数目,有效避免以高阶矩为目标函数进行优化时所带来的求解困难。第三,设计了三步法求解方案,有效区分资产特征变量、动态偏度风险和动态峰度风险等对资产配置权重以及组合投资绩效的影响,为投资者动态修正组合投资选择、有效防范高阶矩风险提供依据。第四,分别对中国股票市场的个股和行业板块指数展开实证,研究结果一致表明:基于MIDAS-QR模型的动态峰度风险测度方法是测度金融市场峰度风险的有效且稳健方法;市盈率、账面价值比和动态偏度风险对组合投资权重产生显著正向影响,条件波动率和动态峰度风险对组合投资权重产生显著负向影响,这些为组合投资决策提供较好的金融机理性解释;考虑动态高阶矩风险的B-S-K模型是组合投资决策的有效工具,不仅帮助投资者更加全面地把握与规避投资风险,而且为投资者带来了更高的风险调整收益。

1 动态高阶矩风险稳健性测度

1.1 动态偏度风险稳健性测度

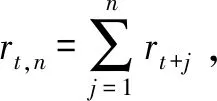
考虑到传统偏度测度方法对异常值的敏感性,已有文献对偏度风险稳健性测度进行了探讨。其中,GHYSELS等[4]将Cornish-Fisher(简称CF)展开与基于分位数的偏度测度方法相结合,并充分考虑金融市场风险的时变性,给出动态偏度风险的稳健测度混合方法:

(1)

式中qα,t-1(rt,n)是MIDAS-QR模型使用高频(日度)收益信息估计的低频期(月度)条件分位数:

(2)

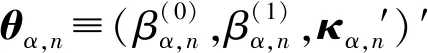
1.2 动态峰度风险稳健性测度

与偏度类似,传统基于矩的峰度测度方法也很容易受到异常值的影响。为此,HOGG[2]提出基于分位数的峰度测度方法:

(3)

式中分子(分母)比较了上分位数1-α(1-β)和下分位数α(β)之间的距离。HOGG[2]通过仿真实验发现,当α=0.05,β=0.5时,RKINT(rt,n)的测度结果最为稳健。

考虑到投资者对收益四阶矩的关注,本文将式(3)中基于分位数的峰度测度方法与四阶CF展开式相结合,同时考虑金融市场中峰度风险的时变性,给出条件信息集Ωt-1下的动态峰度风险稳健测度混合方法:

(4)

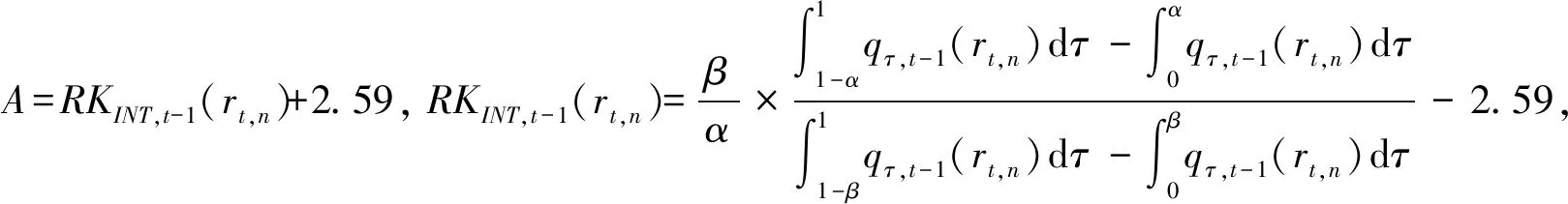
qτ,t-1(rt,n)由式(2)中MIDAS-QR模型估计。本文基于MIDAS-QR模型给出的动态峰度风险测度混合方法RKINT,t-1(rt,n),能够有效提取并及时补充高频数据中的有用信息,其测度的峰度风险不但具有时变性,而且更加及时、稳健和准确。

2 动态高阶矩参数化组合投资决策

2.1 模型表示

假设t-1时刻,有Nt-1个风险资产。理性投资者考虑通过组合投资选择,实现效用最大化[13]。本文选用体现投资者风险厌恶的CARA效用函数,构造投资者效用最大化问题:

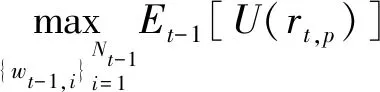
=Et-1[-exp[-γ(1+rt,p)]]

(5)

式中γ>0为绝对风险厌恶系数;rt,p为组合投资收益;rt,i为金融资产的收益;wt-1,i表示t-1时刻分配给金融资产i的权重。

BRANDT等[11]提出参数化组合投资策略,将金融资产特征纳入组合投资决策过程中,显著提高金融资产配置效率的同时,增加了组合投资选择的可解释性。受此启发,本文对组合投资权重进行了参数化设计,将其表示为金融资产特征变量、动态偏度风险和动态峰度风险三方面的线性组合。在特征变量选取方面,本文考虑条件波动率VOL、市盈率PE和账面价值比BTM。已有研究表明这些资产特征对组合投资决策具有重要意义,例如:GHYSELS等[4]发现考虑VOL的影响,可为投资者带来更高的潜在收益;许启发等[14]研究指出投资者配置PE较高的金融资产,能够有效降低投资风险;许启发等[15]讨论了带有BTM的组合投资问题,结果表明考虑BTM帮助投资者获得了更高的投资收益。基于以上分析,将组合投资权重设计为:

(6)

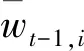
本文构建的B-S-K模型具有明显优势:第一,B-S-K模型形式简单、求解方便,仅需估计较少的参数。对于N个风险资产,在传统的高阶矩组合投资模型中,需要计算N个期望收益、N×N个方差-协方差矩阵、N×N2个偏度-协偏度矩阵以及N×N3个峰度-协峰度矩阵,共计N+N2+N3+N4个参数;在参数化策略构建的B-S-K模型中,需要计算N个动态偏度风险、N个动态峰度风险以及N个组合投资权重,共计3N个参数。易见,对于一N≥2个的组合投资决策,本文基于参数化组合投资策略构建的B-S-K模型,有效缩减了待估计参数的数目,避免了参数估计不准确以及过度拟合等问题。第二,B-S-K模型的参数化组合投资权重设计,同时考虑了资产特征变量、动态偏度风险和动态峰度风险等方面的影响,能够细致刻画出特征变量及动态高阶矩风险对资产配置权重以及组合投资绩效的贡献,为组合投资选择提供了金融机理性解释。第三,B-S-K模型考虑了金融市场的动态风险,可以进行动态组合投资选择,为投资者动态修正资产配置提供了依据。

2.2 模型求解

B-S-K模型的求解本质上是一个非线性优化问题,常用技术包括:遗传算法、粒子群优化算法和梯度下降算法等。已有研究大多将目标函数作为一个整体进行一次性优化求解,存在计算压力与初始值选择两个难点。与之不同,本文基于BFGS算法,设计了三步法求解方案,分步骤求解动态高阶矩风险下的参数化组合投资模型。第一步,估计B模型中特征变量系数λB≡(λVOL,λPE,λBTM);第二步,固定第一步所得结果,估计动态偏度风险系数λSK;第三步,前两步中得到的参数估计值固定不变,基于投资者期望效用最大化估计动态峰度风险的系数λKR。与整体优化的求解方法相比,三步法求解方案具有明显优势:第一,每一步中需要优化的参数数目相对减少,进而缓解了计算压力,缩短了优化时间,提高了模型求解效率;第二,后一步优化以上一步所得结果作为输入,有效降低了对参数初始值的敏感程度,增加了参数估计结果的稳定性;第三,可以分阶段展示B-S-K模型的中间结果,便于比较和分析资产特征变量、动态偏度风险和动态峰度风险等各因素对组合投资权重与绩效的具体影响。

2.3 模型评价

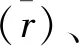
AShR=ShR×[1+(S/6)×ShR-(K/24)×ShR2]

(7)

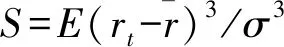
3 实证研究

3.1 数据与描述

以中国股票市场个股为研究对象,随机抽取六支股票作为代表:中国铁建、中国国航、中国银行、大悦城、新世界和红豆股份。数据包括各股票的日度收盘价、市盈率和账面价值比,数据来源于巨灵财经,样本区间为2010年1月4日至2019年9月31日。另外,条件波动率通过混频数据抽样方法计算[4]。

对六支股票日度收益进行统计性描述,发现六支股票的收益率序列均不服从正态分布,且具有明显的尖峰肥尾特征。因此,在组合投资决策中,仅关注收益序列的前二阶矩存在不足,需要考虑收益序列的更高阶矩特征以得到更好的组合投资效果。

3.2 动态高阶矩风险稳健性测度分析

鉴于金融风险的时变性,已有研究采用滚动窗方法测度动态高阶矩风险,然而其局限性不容忽视:第一,滚动窗口长度选择具有较大随意性;第二,损失了原始高频数据中包含的丰富信息。为此,需要进一步讨论具有动态特征的高阶矩风险稳健性测度。运用MIDAS-QR模型估计六支股票月度收益的条件分位数,进一步结合式(1)和式(4),计算动态偏度风险的稳健测度SKINT,t-1和峰度风险稳健测度KRINT,t-1。

从六支股票动态高阶矩风险稳健测度的结果(限于篇幅,结果略)可以得到:第一,样本期间内,六支样本股的SKINT,t-1不为零且在较小范围内波动,表明各样本股具有明显的动态偏度风险,组合投资决策时需要考虑偏度风险并从动态角度进行防范与规避。第二,KRINT,t-1在较小区间范围内波动,呈现出显著的时变特征,表明KRINT,t-1能够动态且稳健地测度金融市场中的峰度风险,可以帮助投资者及时跟踪并把握峰度风险,为其动态修正金融资产配置提供有效依据。第三,六支股票均存在超额峰度,说明样本期间内极端事件发生的可能性较大,需要从高阶矩的角度研究组合投资选择问题,进而较好地避免极端风险的影响。

进一步对六支股票动态高阶矩风险之间的相关性进行分析,发现六支股票动态高阶矩风险之间的相关系数较小,计算相关系数绝对值的均值,可以得到:两两股票SKINT,t-1序列间相关系数绝对值的均值为0.2905,KRINT,t-1序列间相关系数绝对值的均值为0.1796。可见,六支股票动态高阶矩风险之间存在显著的弱相关性,在组合投资决策中考虑动态高阶矩风险,将有助于投资者合理地多样化资产配置,有效地防范和分散投资风险。

3.3 动态高阶矩参数化组合投资决策分析

3.3.1 组合投资结果分析

表1 组合投资模型参数估计结果(个股)

运用三步法求解方案,以投资者效用最大化为目标,估计动态高阶矩参数化组合投资模型参数。本文考虑较低、中等和较高三种不同程度的风险厌恶水平,选取γ为3,5和7。在表 1中,M-V模型和B模型考察了资产特征变量对组合投资权重的影响;B-S模型在B模型基础上,引入动态偏度风险,考察动态偏度风险对组合投资决策的影响;B-S-K模型在B-S模型基础上,纳入动态峰度风险,以考察由动态峰度风险引起的组合投资权重变化情况。

观察表 1中参数估计结果,可以发现:第一,条件VOL对组合投资权重具有显著的负向影响,PE和BTM具有显著的正向影响,说明投资者倾向于增持条件波动率较低、市盈率和账面价值比较高的股票。第二,动态偏度风险的系数在1%水平上显著为正,表明投资者倾向于偏度风险较大的股票。第三,动态峰度风险的系数显著为负,表明动态峰度风险对组合投资权重产生了显著的负向影响,换句话说,在最优资产配置中,股票的动态峰度风险越大,其分配的权重就会越小,这与投资者最小化峰度风险的投资理念相统一。第四,对于三种不同程度的风险厌恶水平,资产特征变量(或动态偏度风险,或动态峰度风险)对组合投资权重的影响方向保持一致,可见本文构造的参数化组合投资决策模型具有稳健性,能够为组合投资选择提供较好的机理性解释。

3.3.2 组合投资效果评价

从收益、风险和风险调整收益等方面,将本文构建的B-S-K模型与等权方案、M-V模型、B模型和B-S模型进行对比分析。

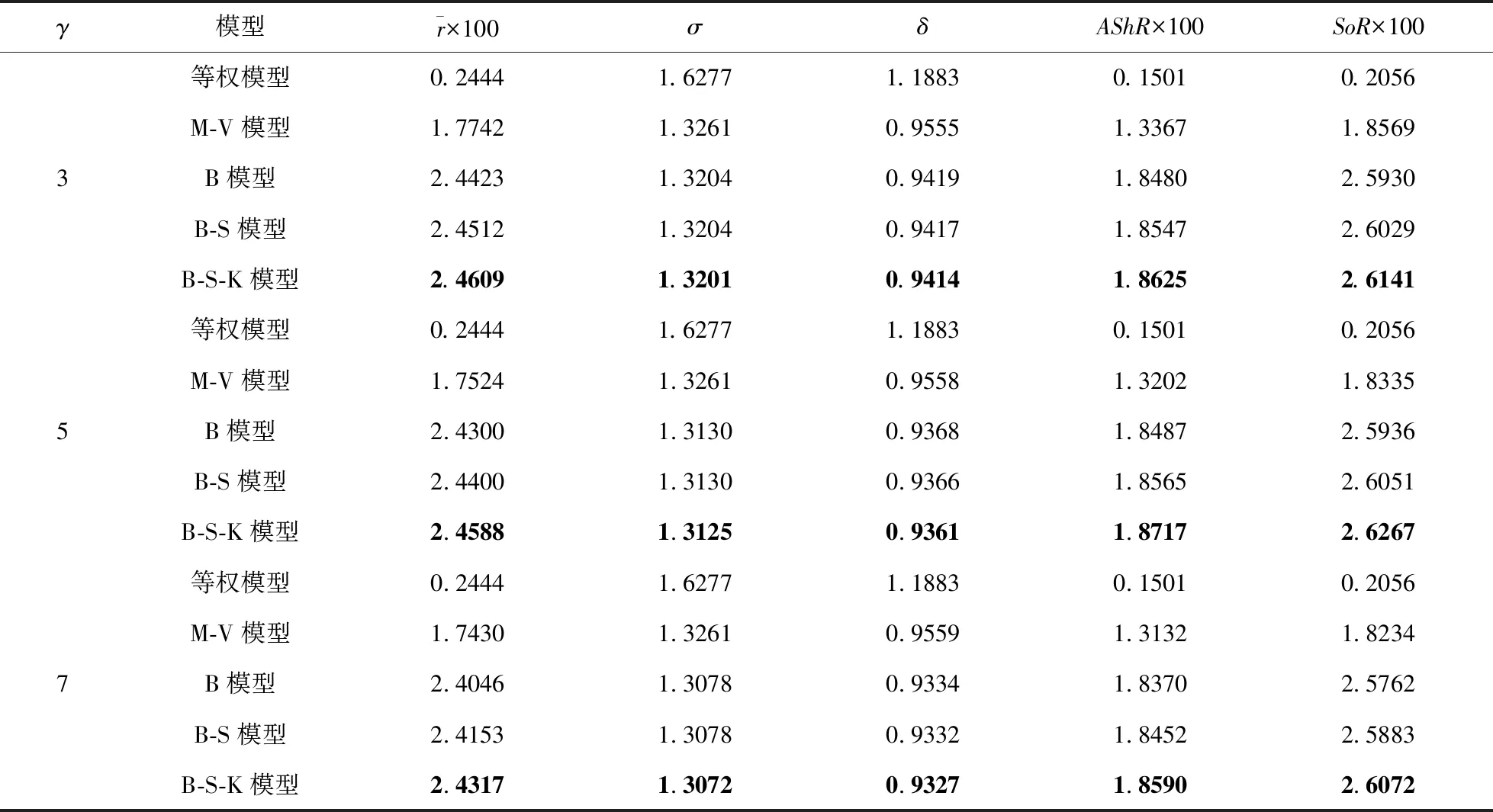
表2 组合投资模型表现(个股)

由表 2可以看出,同时考虑动态偏度风险和动态峰度风险的B-S-K模型具有很好的组合投资绩效。第一,在组合投资收益、风险和风险调整收益等方面,B-S-K模型均表现出显著优势。具体地,B-S-K模型所得的期望收益、调整Sharpe比率和Sortino比率均最大,而标准差和下行风险均最小。可见,B-S-K模型能够为投资者带来较高的收益水平,同时较好地分散投资风险。第二,在较低、中等和较高等三种不同风险厌恶程度下,B-S-K模型的各评价指标都要优于等权方案、M-V模型、B模型和B-S模型,表现出较强稳健性。第三,当风险厌恶水平由低到高时(γ的取值逐渐增加),B-S-K模型所得的标准差和下行风险逐渐减小,组合投资期望收益也在逐渐减小,对应的调整Sharpe比率和Sortino比率在γ=5时达到最大值。这些结果表明,B-S-K模型帮助投资者有效地规避组合投资风险,能够为(尤其是具有中等风险厌恶水平的)投资者带来较高的风险调整收益。

综上述,动态偏度风险和动态峰度风险对组合投资决策都产生了显著影响。本文构建的动态高阶矩参数化组合投资模型(B-S-K),同时考虑了这两种具有时变特征的高阶矩风险。与等权方案、M-V模型、B模型和B-S模型等相比,B-S-K模型在收益、风险和风险调整收益等方面均表现最优,并且在不同风险厌恶水平下具有稳健性。由此可见,B-S-K模型是组合投资决策的有效工具,能够为不同风险厌恶水平的投资者带来更好的组合投资效果。

4 稳健性检验

4.1 检验过程说明

第一,数据选取。这里以中国行业板块指数为研究对象,选取中国证监会行业分类指引(2012年版)中的行业板块,剔除数据缺失严重的居民服务和修理行业,剩余18个行业板块。考虑到行业板块是处于同一行业的股票集合,这里选用行业指数的条件波动率、市盈率和账面价值比等作为特征变量。

第二,高阶矩风险测度。运用MIDAS-QR模型测度具有动态特征的高阶矩风险。首先,通过MIDAS-QR模型使用高频(日度)收益信息估计18个行业板块指数n期(月度)收益的条件分位数;其次,将条件分位数结果分别代入式(1)和式(4),计算各行业板块指数的动态偏度风险和动态峰度风险。

第三,组合投资决策。运用动态高阶矩参数化组合投资模型(B-S-K),研究18个行业板块指数的组合投资决策。首先,将行业板块指数的特征变量、动态偏度风险和动态峰度风险引入组合投资权重函数,联合CARA效用函数,构建B-S-K模型;其次,运用三步法求解B-S-K模型参数;最后,从收益、风险和风险调整收益三个方面,与等权方案、M-V模型、B模型和B-S模型进行比较,评价本文构建的B-S-K模型应用于中国行业板块指数的有效性和稳健性。

4.2 检验结果分析

(1)高阶矩风险测度结果分析。18个行业板块指数的高阶矩风险测度结果(限于篇幅,结果略)表明:样本期间内,各行业板块指数的高阶矩风险在较小区间范围内波动,并且较少出现极端取值,测度结果受异常值的影响相对较小,总体较为稳健;极端事件的发生,对各行业板块指数的高阶矩风险产生了显著影响,例如2015年股灾、2018年贸易争端以及2020年新冠疫情期间,大多数行业板块指数的动态偏度风险SKINT,t-1(rt,i)呈现负值,动态峰度风险KRINT,t-1(rt,i)值较大,证实了高阶矩风险测度结果的有效性。可见,基于MIDAS-QR的动态高阶矩风险测度方法能够同样有效地测度18个行业板块指数的高阶矩风险,其测度结果具有时变性和稳健性,能够为投资者及时跟踪高阶矩风险、实现资产动态配置提供有效参考。

(2)组合投资结果分析。为检验本文构建的动态高阶矩参数化组合投资决策模型(B-S-K)的稳健性和有效性,进一步分析18个行业板块指数的组合投资结果,包括模型参数估计结果和模型表现结果(限于篇幅,结果略)。此处仍然考虑等权方案、M-V模型、B模型和B-S模型等对比模型,同时考虑较低、中等和较高等三种不同风险厌恶程度,对应γ取值分别为3,5和7。

综合以上,可以发现在组合投资模型参数估计和绩效表现等方面,运用18个行业板块指数数据得到的结果与运用六支个股数据得到的结果较为一致。因此,本文构建的参数化B-S-K模型不仅适用于需要灵活配置的单支股票间组合投资决策问题,而且可以运用到反应市场整体发展态势、具有中长期投资价值的行业板块指数研究中,具有较好的稳健性和有效性。

5 结论

本文构建了动态高阶矩参数化组合投资决策模型(B-S-K)。一方面,基于MIDAS-QR模型给出动态峰度风险稳健性测度方法,充分挖掘原始高频数据信息,提高动态峰度风险测度的及时性、稳健性和准确性。另一方面,引入参数化组合投资框架,同时考虑动态偏度风险和动态峰度风险,构建包含动态高阶矩风险的参数化组合投资模型,并基于BFGS算法给出三步法求解方案。B-S-K模型不但大幅缩减待估计参数的数目,避免以高阶矩作为目标函数的组合投资模型的求解困难;而且量化资产特征变量、动态偏度风险和动态峰度风险等对组合投资权重和组合投资绩效的具体贡献,增加组合投资选择可解释性,为投资者动态修正资产配置提供决策依据。

为检验B-S-K模型有效性,考察动态高阶矩风险稳健性测度与参数化组合投资决策的效果,分别选取中国股票市场的六支个股和18个行业板块指数展开实证,研究结果一致表明:第一,动态高阶矩风险稳健性测度方法是测度金融市场高阶矩风险的有效方法,其测度结果受异常值影响较小;第二,动态偏度风险和动态峰度风险均对组合投资决策产生了显著影响,不同风险厌恶水平的投资者在进行组合投资选择时,往往都偏好具有较大偏度风险和较小峰度风险的股票;第三,条件波动率、市盈率、账面价值比、动态偏度风险、动态峰度风险等都与组合投资权重呈现出显著的相关关系,这些为组合投资决策提供较好的金融机理性解释;第四,与等权方案、M-V模型、基准(B)模型和B-S模型等相比,本文构建的B-S-K模型在收益、风险和风险调整收益等三个方面均表现出显著且稳定的优势。