基于层间互信息的时序网络节点重要性识别方法
2023-09-25邓志文李新春王大阜
邓志文, 李新春, 孔 杰, 王大阜
(1.中国矿业大学 图书馆,江苏 徐州 221116; 2.中国矿业大学 经济管理学院,江苏 徐州 221116; 3.国网湖南电力有限公司,湖南 益阳 413506)
0 引言
随着当前各种社交网络平台的蓬勃发展,复杂网络分析逐渐受各学科领域研究者的广泛关注。Internet、社交网络、科研合作网络和论文引用网络等都可以用复杂网络进行描述和研究。网络节点重要性识别是复杂网络研究中一项重要内容,它在信息扩散机制与控制、广告营销策略制定等多个领域具有广泛应用。现有网络节点重要性识别方法主要基于网络全局、局部的结构特征,或者基于网络中节点在所处的位置,再或者基于网络动力学特征,这些方法都是基于与时间无关的静态网络,与之不同,时序网络考虑了节点之间交互关系和时间次序,可以更加准确地刻画手机通讯、社交等复杂系统的交互关系[1]。
时序网络带有时间信息,其边会随着时间的变化出现或者消失,和传统静态网络的拓扑结构存在较大差异,网络数据除了节点和边外,还包含接触时间信息,因此识别其中节点重要性的方法较传统方法也有很大不同。近年,学者们关于时序网络节点重要性识别方法开展了一系列研究,归纳起来主要分为三个主要方向:
(1)传统复杂网络分析。TANG等把连续的时序网络切成相等的时间片,通过网络介数中心性和接近中心性计算节点重要性[2];KIM和ANDERSON通过线图模型,计算网络度中心性、介数中心性以及紧密中心性来度量时序网络节点重要性[3]。
(2)结合传播动力学。邓冬梅等基于节点边缘贡献度和节点的感染方式评价节点重要性[4];HUANG和YU通过引入动力学相反方法对时序网络节点重要性进行度量[5]。
(3)系统结构科学。杨剑楠等基于节点层间相似性的超邻接矩阵对节点在各个时间层上的重要性排序,并通过节点删除法判断节点的影响力[6];郭强等应用TOPSIS方法对时序网络层间关系选择,挖掘时序网络中的重要节点[7]。
另外其它文献从不同角度来研究,如文梁耀洲等[8]基于评分矩阵的排名聚合理论,提出了一种基于排名聚合的时序网络节点重要性识别方法;胡钢等[9]通过网络层间同构率动态演化的超邻接矩阵建模对时序网络中的节点重要性排序。已有的研究从不同角度出发开展讨论,取得了很好的研究成果,也存在不足。复杂网络可看成一个复杂的通信系统模型,将边看作信息流,则节点的信息量可以度量其相对重要性。马润年等[10]通过计算静态网络节点边的概率分布求得与其相连节点之间的互信息量,然后对节点互信息求和作为其重要性评估指标,而时序网络中网络结构的变化会导致层间信息传递量改变,WU等[11]针对时序网络,用边概率分布从全局量化这种层间信息传递的相互关系。但度量节点重要性更需要考虑单个节点在层间所发生的这种信息量变化的过程,具有局部特征,基于此本文提出一种基于层间互信息的时序网络节点重要性计算方法。该方法基于时间窗口模型,计算各时间窗口内网络特征向量指标,通过节点边在时序窗口的概率分布和相邻窗体间节点的联合概率分布计算节点在层间的互信息值,将其作为节点在各时间窗口的时序系数,再结合以上两个结果综合评估时序网络内各节点的重要性。最后,利用修改的SIR模型,在公共测试数据集上进行实验,实验结果证明了本方法的优越性。
1 相关定义
1.1 时序网络模型
时序网络是一个含有多个对象及对象间按时间排列的相互作用系统,其中对象视为节点,对象间的相互作用视为关系。令G(V,E)表示一个无向无权的时序网络,其中:V为时序网络中所有节点的集合;E为时序网络中所有边的集合,用三元组eti(vi,vj,t)表示节点之间的时序交互,即节点vi和vj在t时刻产生交互,如图1所示。
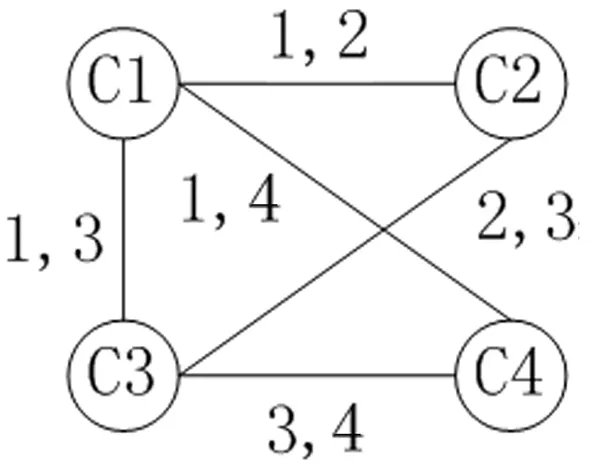
图1 时序网络
令A表示时序网络G所对应的邻接矩阵,相比静态网络,A中元素aij值是节点i和j所有交互时间点集合[t1,t2,…,tn],如下图所示,其对角元素为0。
如果节点vi和vj之间存在连边,则其元素aij=1,否则aij=0。在复杂网络研究中,网络节点重要性识别方法如基于网络全局、局部的结构特征,或者基于网络中节点在所处的位置,其都是基于节点所处的周围环境进行定量计算,都用到了复杂网络理论中的一个重要概念特征向量中心性。
1.2 特征向量中心性
中心性用来衡量一个节点在网络中处于核心地位的程度,目前有四种中心性的分析方法,分别是:度中心性、间接中心性、紧密中心性、特征向量中心性[12]。特征向量中心性度量的是节点影响的传递,其值即与节点本身的重要性有关,也与其相邻的其它节点的重要性相关,记xi为节点i的重要性度量值,则:
其中,c为一个比例常数,aij表示矩阵A中节点vi和vj之间是否存在连接,aij为1时表示节点间存在连接,值为0表示无连接。
记x=[x1,x2,…,xn]T,经过多次迭代计算到达稳态时,可以表示为如下的矩阵形式:x=cAx。
以上公式x表示的是矩阵A的特征值c-1对应的特征向量,也可以写成如下形式:Ax=λx。
其计算过程:
(1)计算邻接矩阵初始特征向量x(0);
(2)利用公式x(n)=cAx(n-1)依次迭代计算;
(3)当x′(n)=x′(n-1)时,迭代结束;
(4)选择有最大特征值的特征向量,其中特征向量中的第i个元素作为第i个节点的中心性。
一个节点特征向量中心性的值与其相邻节点的中心性值的和成正比,也就是重要的节点周围的节点相比也更重要,有少量重要的节点其中心性值有可能超过拥有大量平庸相邻节点的节点。邻居节点本身的重要性会影响所评价节点的重要性。
1.3 时序窗口
时序网络中边具有时效性,它会随时间的变化而变化。现有常用研究方法是将时序网络中连续的时间段划分成等时间间隔的多个时间窗口,同一时间窗口构成一个网络片段,最后生成一个连续的切片网络序列,如图2。

图2 长度为6时序网络序列
定义时序窗口:假设时序网络总时间长度为[0,T],设每个时间段长度为t,则窗口数为M=T/t。如上图将时序长度设为2,则窗口数为3,如图3。
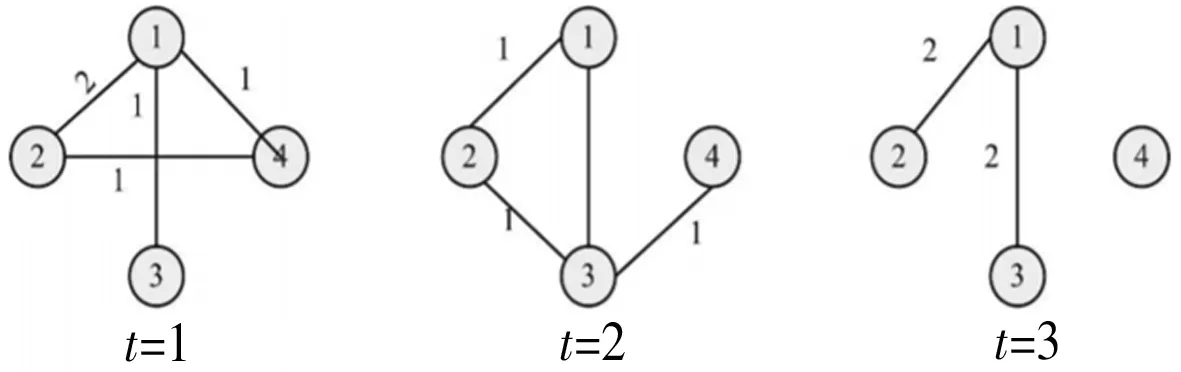
图3 长度为3时序网络序列
不难看出,对于同一数据集,时序窗口的大小设置不同,最后所得的时间窗口个数和各个窗口内的网络节点连边情况也不相同。
2 基于层间互信息的节点时序相关系数计算
传统的静态网络通过在边上加上权值来衡量两节点间的关系强度,且这个权值一般都是对节点间发生关系次数的直接累加。社交网络中节点的重要性度量实际上是反应的节点影响力,从信息论角度思考就是节点传递给其它节点的信息量,在时序网络中每个时序窗口的网络结构不同,其节点传递的信息量也不一样,通过关系次数的直接累加会丢失时序窗口间网络结构变化以及节点信息传递量变化的信息。WU等[11]从全局角度通过连边概率分布和联合概率分布计算层间的互信息值,进而得出网络各层间整体相关性值,节点的重要性度量需要关注节点在时序窗口间相关性,因此本文结合WU等[11]从节点连边概率分布出发设计算法模型计算节点间的相关性,并通过定义相关性系数矩阵作为时间窗口间节点的信息传播变化量值,下面本文讨论相邻层间节点相关性系数计算方法。
2.1 时序节点相关性矩阵

2.2 节点层连边概率分布计算
时序网络中各层并不是完全独立的,比如会存在一些边的重叠,不同层的同一节点往往倾向于有相同的网络结构特性。当在时间窗口[t2,tn]时,第n个时序窗口用n位的二进制数a来描述某个节点i在第n个时间窗口连边状况,如果节点i与节点j在1至n个时间窗口中某个窗口存在边,则a对应元素表示为1,否则为0,最后将这条边作为一个概率分布的实例。计算公式如下:
上式中N为网络节点数,count(tn)计算的节点i在第n个窗口所有相同a值数,其第n层节点i的信息熵公式:
如图4第三个时序窗口中节点A可用表1表示其连边概率分布值。

表1 层内节点边概率分布表
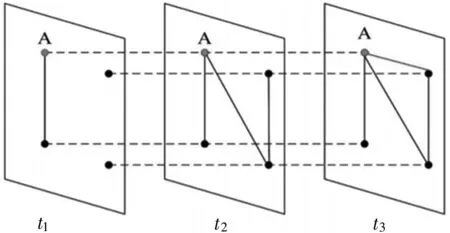
图4 时序网络边变化
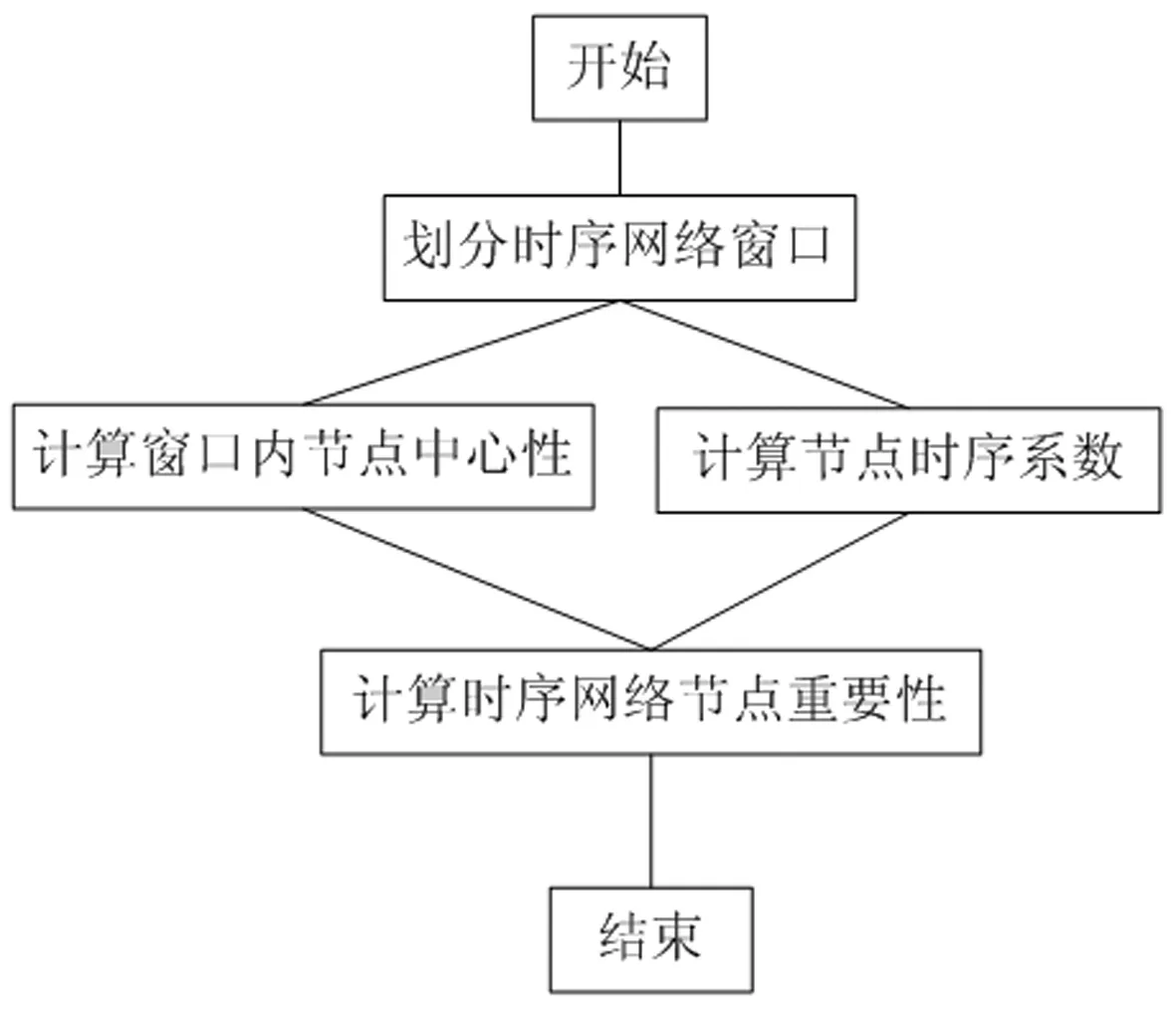
图5 时序网络节点重要性计算流程图
2.3 节点相邻层联合边向量概率分布
用两位二进制数b来描述某个节点i在相邻两层窗口连边状况,用公式Hi(tn,tn+1)表示节点i在相邻层间的联合信息熵,如上图4节点A在t2和t3相邻窗口间连边的联合概率分布如表2。

表2 层间节点连边联合概率分布表
2.4 节点层间相关性系数
信息论中一个随机事件它结果越稳定则所传递的信息量越小,相应的在时序网络中如果两个节点在连续的多个时序窗口间保持稳定关系,则这对节点间所传递的信息量也会变少。信息论中互信息常用于表示信息之间的关系,是两个随机变量统计相关性的测度,已知事件A和事件B,如果他们的互信息值越高,则它们的相关性也越高,因此互信息也多用于评价多个属性的关键程度和属性重要性的计算。本文通过计算节点在层间的互信息用于衡量节点在相临层间的相关性。在[t2,tn]内,相邻两层间节点的相关性可用下式表示:

3 时序网络节点重要性计算方法
3.1 时序窗口特征向量
通过时间分割,时序网络形成了连续不等的切片网络序列,一个有n个节点的时序网络,假设被切分成了t个时间窗口,通过求层间联合边向量概率分布、层间相关性系数等得出每个时间窗口节点对应的特征向量中心性值,公式表示如下:
Ei=[e1,e2,e3,…,en],i∈[1,t]
3.2 时序网络节点重要性计算
时序网络由多个时序片段组成网络序列,单个网络片段中节点的中心性无法反应整个网络序列节点重要程度,但节点重要性计算结果应反映节点在局部时间节点的特征以及全局的变化情况,因此本文设计时序网络节点重要性计算算法的基本思想为:节点在不同时间窗口间的影响力与其信息传递量的变化有关,也就是2.4节中所计算的节点时序相关系数,系数越大,节点相比上一个时间窗口变化也越大,所传递的新信息量也越多。为了得到节点重要性计算的综合值,借鉴加权计算思想,将节点时序相关系数作为节点在各时序窗口中的加权系数,以衡量不同窗口间节点的重要性差异,通过加权计算得到节点在整个时序网络下的整体值。其重要性计算过程如下:
步骤1划分时序窗口M=T/t。
步骤2计算各个时间窗口内各个节点的特征向量中心性。
步骤3计算相邻时间窗口的相关性系数矩阵Kt,t+1。
步骤4计算时序网络节点重要性值W(i):
上式中W(i)表示时序网络中节点的重要性值。
4 实验分析
4.1 数据描述
本文采用Manufacturing和Enrons真实社交数据来检验本方法在时序网络节点重要性计算的效果。Manufacturing和Enrons两个数据集为公司员工之间邮件联系数据集。
数据集Manufacturing收集了某公司内部员工之间通过电子邮件进行通信的交互记录,其通信日期从2010年1月至2010年9月;数据集Enron收集的是某公司内部高层管理人员之间通过邮件从2000年到2002年共两年的通信记录。本文将两个数据集中的员工抽象为网络的节点,员工之间的通信记录抽象为网络节点之间的连边,交互时间则对应每条连边的时间属性值,按月进行时间切分。统计结果如表3。其中N表示总节点数,T表示切分的时序网络数,C表示节点之间的总交互数,E表示网络的连边数。

表3 实验数据集
4.2 对比方法
K-核分解法是常用的静态网络节点重要性计算方法,该方法通过递归依次将节点分成不同的层次,每一层中节点越靠近网络中心位置节点重要性越大。时序K-核分解法则将静态方法扩展到时序网络中[13],该方法计算节点重要性不仅反应了网络的拓扑信息、网络节点全局情况,也综合考虑了网络各个节点的时序关系影响,因此本文以时序K-核法进行对比分析。
4.3 方法评价
静态网络中评价节点重要性方法是计算其准确性,它通常是与一种经典标准模型算法对比并计算算法的关联度,关联度越高,则算法准确性越高,本文使用SIR模型作为衡量标准。
传统的SIR模型[14]不包含时序信息,直接将SIR模型应用到时序网络中会造成实验结果的不准确性。在网络传播中同一对节点在不同时序窗口都有连边,节点间交互频率高,则这对节点间在网络中被传播的概率也就高。基于此,本文参考朱晓霞和胡小雪[15]的研究对传统SIR模型进行调整。
设时序网络各时间窗口t1,t2,t3,…,tn的传播概率为c1,c2,c3,…,cn,其中ci的取值范围为[0.01,0.2],如果节点对(i,j)之间在时间窗口t1,t2,tx有连边,则时序网络节点i对节点j的感染概率计算如下:
pi=1-(1-ci)(1-c2)(1-cx)
设SIR模型和所验证算法的节点的排序结果分别为X和Y,X={x1,x2,x3,…,xn},Y={y1,y2,y3,…,yn}。任意节点对(xi,xj)和(yi,yj),如果满足xi>yi和xj>yj,或者xi 其中nc表示协同节点对数量,nd表示非协同节点对数据,i(X,Y)值越高表示该算法的准确性越高。 本文通过与时序K-核分解法进行对比实验。基于层间互信息的时序网络节点重要性计算方法简称IG, 时序K-核分解法简称TKs,为了便于计算,实验中将各时间窗口的传播率ci都设为相等值,并通过不断修改ci的值来观察i(X,Y)的变化,Manufacturing数据集实验结果如图6。 图6 Manufacturing实验结果 从图6看出,实线的值要高于虚线,也就是本文给出的方法计算得到的节点重要性的准确度相比高于时序K-核分解方法,证明本文方法的排序结果存在一定的优势。 图7中Enron数据集中IG重要性排序的准确性依然要高于时序K-核分解方法,同时从曲线波动性不难看出其准确性稳定性也较高。从SIR模型分析,因为SIR模型中即有易感节点被感染概率,同时也要考虑被感染节点恢复后重新被感染的概率以及节点的反感染作用,实际上SIR模型这种复杂的相互影响关系可以看成一种网络关系随时序复杂变化的过程,与本文求层间节点相关性系数方法具有一定相似性,因此通过SIR模型验证本文方法其关联度更高。 图7 Enron实验结果 本文基于时间窗口模型,通过时序窗口层的特征向量计算获得了局部时间的节点中心性值,同时结合信息论相关理论从网络结构中连边变化出发计算相邻时间窗口间节点变化的相关性用于度量信息传递的变化量,结合两种结果计算求得时序网络节点重要性,根据修改后的SIR模型来评估算法准确性,并对比时序 K-核分解方法可得本文方法的节点重要性计算结果相比具有一定的优越性。但本文仅对相邻时间窗口间节点相关性变化分析,存在一定局限,丢失了整体或多个时间窗口所隐含的信息,因此如何结合多个时间窗口或全局去衡量网络中节点关系的变化是需要深入研究的问题。4.4 实验分析


5 结语
