基于随机恢复时间的骨盆骨折创伤患者手术分配优化
2023-09-25邓国英
李 清, 苏 强, 邓国英
(1.上海政法学院 经济管理学院,上海 201701; 2.同济大学 经济与管理学院,上海 200092; 3.上海市第一人民医院 创伤中心,上海 201620)
0 引言
骨盆骨折是由骨盆直接挤压引起的严重创伤,常伴有其他器官和系统损伤,致残率高达50%~60%。近年来,机动车和工伤事故频繁发生,骨盆骨折已成为骨科常见的损伤[1]。严重的骨盆骨折会导致失血性休克和重要脏器损伤,救治不当会产生高达10.2%的死亡率。根据骨盆的稳定性,骨科创伤协会采用Tile分型方法将其分为A稳定型,B部分稳定型和C不稳定型三类[2],B型和C型患者通常建议手术治疗。骨盆骨折急救遵守创伤生命支持原则,首先抢救生命,生命体征稳定后再进行相关检查,确定创伤类型,制定骨折手术计划。在医疗资源共享背景下,优化手术安排,合理分配医疗资源至关重要。本文创新点如下:
(1)根据患者入院时生命状态将其分为恢复期和计划期两类,恢复期患者经过随机恢复时间到生命稳定状态后手术。(2)建立马尔科夫决策过程模型,得到最优分配策略,分析最优策略结构性质。(3)调整恢复期患者的恢复时间、数量和参数,设置不同形式惩罚函数,进行敏感性分析。
1 文献综述
手术是医院重要的收入来源,也是不可忽视的成本中心,手术资源利用直接影响手术服务水平。在预约调度和手术分配方面,以传统预约排期模型为基础,XIAO等[3]建立三类患者临床预约的随机规划模型,采用先进调度方法优化性能指标。LIU等[4]考虑不同部门的计划和容量,统计住院时间和住院人数,建立MDP模型制定每日手术安排计划。
医疗设备动态分配方面,朱黎敏等[5]考虑三类患者,以最大化满足患者检查为目标建立有限阶段马尔科夫决策支持模型,制定最优预约调度策略。针对CT室的管理,周杰等[6]以最大化系统期望收益为目标,建立MDP模型,制定不同容量的管理策略,研究不同策略对患者等待时间的影响。GENG和XIE[7]考虑两类不同等待时间和收益的患者,建立MDP模型,优化门诊调度。刘阳和耿娜[8]考虑患者不同需求、患者失约和医生加班等情况,以最大化检查的期望收益和最小化加班惩罚成本为目标,建立有限时间MDP模型。
考虑随机因素是手术调度研究的热点。基于随机手术时间、住院时间和手术室容量有限等情况,SHEHADEH和PADMAN[9]以最小化手术成本和延误成本为目标建立混合整数非线性规划,设计自适应列约束生成算法求解。SAADOULI等[10]综合考虑手术时间和恢复室容量的不确定,研究骨科手术患者的择期手术排序问题。JIANG等[11]考虑手术时间随机和患者随机缺席情况,建立分布式鲁棒优化模型,对手术室调度问题进行优化。
已有研究多面向全院患者,设计一台或多台设施的分配策略。本文聚焦创伤领域,为骨盆骨折患者制定手术分配策略。第2节建立马尔科夫决策过程模型;第3节设计实验,分析得出相关结论;第4节总结全文,指出文章不足和未来拓展研究。
2 考虑随机恢复时间的马尔科夫决策过程模型
2.1 问题描述
本文将手术患者分为恢复期和计划期两类,计划期患者入院时生命状态稳定,确定骨折类型后制定手术方案。生命状态不稳定的患者首先抢救生命,术后恢复至稳定状态再接受骨盆骨折手术,这类患者为恢复期患者。恢复时间受到患者年龄、身体状况和骨折类型等因素影响,设置随机恢复时间。系统中同时存在两类患者时,从中选择一类患者进行手术,以最大化期望收益。
2.2 模型建立
每次选择一个患者进行手术,产生收益;满足条件而没手术的患者在队列等候,产生等待成本;规划期结束仍没手术的患者产生惩罚成本。
符号的定义和说明如下:

T(t=1,2,…,T):服务周期总数α=0.1,2:决策集合c:恢复期患者s:计划期患者rti(i=1,2,…,n):恢复期患者恢复时间at∈{0,1}:t周期计划期患者的预约计划rc:恢复期患者每台手术收益rs:计划期患者每台手术收益wc:恢复期患者每周期等待成本ws:计划期患者每周期等待成本kc:恢复期患者的惩罚成本ks:计划期患者的惩罚成本prti∈[0,1]:不同恢复期患者的到达概率ps:计划期患者接受手术的概率ct:t周期等待手术的恢复期患者st:t周期等待手术的计划期患者nct:t周期进行手术的恢复期患者数量nst:t周期进行手术的计划期患者数量cut:t周期后没有手术的恢复期患者数量sut:t周期后没有手术的计划期患者数量S=(ct,st):t周期状态空间Vαt(ct,rti,st):t周期状态S选择决策α的收益f(cut,sut):惩罚函数线性形式:f(cut,sut)=-cut·kc-sut·ks非线性形式:f(cut,sut)=-c2ut·kc-s2ut·ks
本文以最大化期望收益为目标,建立有限阶段马尔科夫决策过程模型,采用后向迭代算法求解。
(1)状态空间
系统状态采用向量S=(ct,rt0,st)表示,其中,st表示第t周期等待手术的计划期患者数量;ct,rt0表示第t周期恢复时间为0的恢复期患者数量。ct,rti(i=1,2,…,n)表示第t周期恢复时间为i的恢复期患者数量。
(2)决策集合
3种决策,α=1选择恢复期患者手术,α=2选择计划期患者手术,α=0不选择患者手术。
(3)转移概率
计划期患者以概率pt(st+1|st,αt)转移到t+1周期,如式(1)。
(1)
αt为第t周期决策;nst为第t周期手术的计划期患者数量,αt=2时,nst=1。
恢复时间为0的恢复期患者,其转移概率为式(2)。
pt(cr+1,rt0|ct,rt0,αt)
(2)
nct表示第t周期手术的恢复期患者数量,αt=1时,nct=1。恢复时间为i的恢复期患者,其转移概率如式(3)。
pt(cr+1,rti|ct,rti,At,rti)
(3)
At,rti为患者的联合到达概率。
(4)收益函数
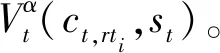
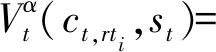
(4)
式(4)是一个递归结构,其详细展开式如式(5)。
(5)
(6)
t周期有ct,rt0个恢复期患者和st个计划期患者,等待成本为-ct,rt0·wc-st·ws。若恢复时间为1的恢复期患者在t周期到达,且无计划期患者,概率为pt,rt1·(1-ps·at+1),系统进入新状态(ct,rt0+1,st);若计划期患者按时接受手术,且恢复时间为1的恢复期患者在t周期到达,概率为pt,rt1·ps·at+1,系统进入新状态(ct,rt0+1,st+1)。最优决策见式(6)。
式(6)的最终状态见式(7)。
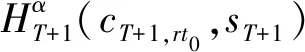
(7)
式(7)为未手术患者的惩罚成本。
该问题的目标函数如式(8)。
(8)
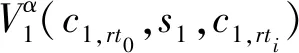
3 案例分析与讨论
采用Matlab R2013a自带求解器,笔记本电脑的操作系统为Windows 7,CPU为:Intel Core i3-3227U,主频为1.90 GHz,内存为4GB。
3.1 数据收集和参数设定
收集上海市第一人民医院2015~2020年骨科的数据,设置3种恢复期患者,其恢复时间分别为1,2和3,参数设置见表1。等待成本等于每日住院费用加每日平均工资,等待帮助恢复期患者达到更稳定的生命状态,因此其等待成本小于计划期患者。规划期末没有安排手术的患者将流失,恢复期患者有更高的收益和风险,因此其惩罚成本大于计划期患者。

表1 参数设置
3.2 实验结果与讨论
(1)决策路径分析
初始状态(期初各患者数量)和各服务周期患者到达情况已知,考虑8个服务周期,求解MDP模型得到状态路径(各周期等待患者数量)和决策路径(各周期决策),见表2。

表2 决策路径分析
(2)最优分配策略——开关曲线
任一周期患者的最大数量为ct,rt0=st=5·t。第三个周期中患者最多等待人数为15,本文采用第三个周期来解释最优分配策略。
采用非线性惩罚函数得到最优分配策略,如图1。该场景有3个恢复期患者,其恢复时间分别为1,2和3,ct,rti=1,i=1,2,3,记为S1(1-1-1)。

图1 S1(1-1-1)的最优分配策略(t=3)
在任一服务周期,给定计划期患者数量,当恢复期患者数量小于关键指标时,选择计划期患者手术,反之,选择恢复期患者手术。开关曲线展示了实时动态资源分配情况。
(3)关键指标单调性

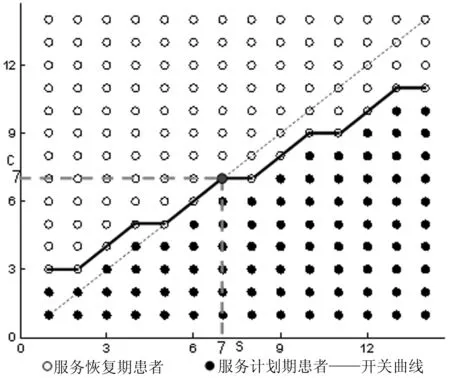
图2 S3(1-1-2)最优分配策略

图3 S4(1-4-1)最优分配策略
(4)关键指标与恢复期患者数量的关系
假设恢复时间为1,2和3的恢复期患者数量最多为6,4和2个,构造48(6×4×2)种场景。i-j-k分别表示3类恢复期患者数量。定义5种场景:S1,1-1-1;S2,0-0-0;S3,1-1-2;S4,1-4-1;S5,6-1-1。表3比较了各场景下ncp,Δn和Δcr的值。ncp表示恢复期患者数量,Δn表示S1与其他场景ncp的差值,Δcr表示S1与其他场景关键指标的差值。

表3 不同场景下关键指标值的比较(t=3)
综上,ncp相同的场景有相同分配策略,ncp=6和ncp=7除外。ncp相同,恢复时间为1的恢复期患者为1个时,最初的2-3个关键指标与其他场景不同,后续值一样。当恢复时间为1的恢复期患者数量大于1时,恢复期患者比计划期患者享有优先权。
S1与其他场景关键指标差值≤S1与其他场景间ncp差值;随着计划期患者的增加,不同场景间关键指标差值不断增加,直至到达最大值ncp。关键指标值越大,恢复期患者优先权越低;ncp越大,恢复期患者优先权越高。
(5)恢复期患者数量对最优策略的影响
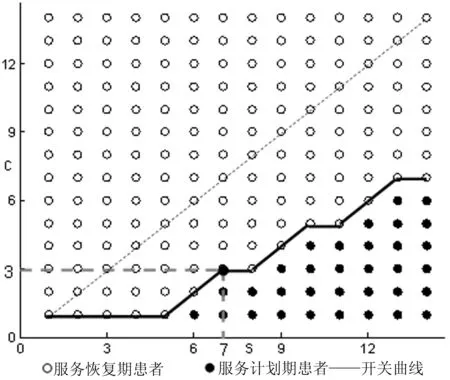
图4 S5(6-1-1)最优分配策略

4 结论
本文在有限规划期内,研究了计划期和恢复期两类骨盆骨折创伤患者的手术安排问题。收集上海市第一人民医院的数据,设计患者参数,得到如下结论:
(1)惩罚函数采用二次函数形式时,最优分配曲线呈现出开关曲线形式。惩罚函数为一次函数时,选择哪一类患者手术取决于患者参数。
采用二次函数形式的惩罚函数时,有以下结论成立。
(3)在任一服务周期,恢复期患者总数相同的场景通常有相同的分配策略,ncp=6和ncp=7时存在例外。恢复期患者数量越多,其享有的优先权越高。此外,各场景关键指标差值小于等于不同场景中ncp的差值,随着计划期患者数量增加,关键指标的差值呈现出逐渐增大的趋势。
本文也存在较多不足:首先,初始状态随机设置患者数量;其次,没有考虑患者批量到达的情况,模型中假设每个服务周期只有一个患者到达。再者,由于骨盆骨折类型、患者身体情况和手术方案不同,手术时间因人而异,文中假设手术时间为一个服务周期。未来研究中,应考虑上一规划周期未手术的患者数量,设置合理的系统初始值。根据实际情况修改患者的到达模式,延长规划周期,作出连续决策,更符合现实情况。
