基于等级置信度的灾后初期多阶段时限派遣模型
2023-09-25李晓超
李晓超, 张 雷,2
(1.浙江财经大学 工商管理学院,浙江 杭州 310018; 2.新疆大学 经济与管理学院,新疆 乌鲁木齐 830046)
0 引言
我国是世界上破坏性地震发生频率较高、灾害损失较大的国家之一。2000—2020年,我国因地震伤亡人数占全球地震伤亡总数的18%。因此,如何最大程度地减少灾区人员伤亡成为我国应急救援行动决策中需要解决的重要问题之一[1]。
破坏性地震发生后,决策者往往需要考虑多个阶段不同情景下的不同派遣任务并做出连续多阶段动态决策[2-4]。多阶段应急决策问题中,前一阶段的决策将对后一阶段决策产生影响,因此,决策者必须考虑相邻阶段决策的关联性[5-9]。杨文国等[5]针对应急救援过程中信息流多变的特征以总的加权救助时间最小化为目标构建救护车分配优化模型;朱莉[6]以绝对和相对总成本最低、救援总耗时最短为多决策目标,构建兼顾效率和公平的跨区域协同应急救援模型;姜艳萍等[7]运用风险决策的方法分析信息不断完善的过程中如何对已经执行的应急方案进行调整;陈兴等[8]建立多阶段多目标多部门应急协同决策模型并随事态发展对决策进行动态调整;姜艳萍等[9]考虑多阶段子方案间相容性并提出一种决策方案链的选择方法。另一方面,震后救援工作具有明显的时效性,时间约束是应急救援方案不可或缺的限制条件,张雷等[10]以最短到达时间为约束条件构建基于优先权的震后时限多目标指派模型。救援效率的高低直接决定了灾区人员伤亡减少程度,樊治平等[11]以完成各救援任务效果最好为目标构建多目标救援人员分组优化模型;张雷和孔艳岩[12]考虑震后受灾点救援力量的实际需求,以应急救援效率最大化为目标确定了应急救援队伍分组方案;张淑文等[13]考虑出救点选择和救援队伍特征,根据不同灾情允许的最大救援时间研究救援队伍运送优先级对救援时间和救援效果的影响。
由上述文献可以看出,动态连续性及应急时限性是震后初期救援主要特征,然而少有文献对其进行统一考虑。另一方面,震后初期受灾及救援信息具有明显的未知不确定性,而救援队伍相对于各受灾点救援效率的合理评估是实现有效救援的前提,现有文献少有涉及。证据推理(ER)适用于包含不完整、不精确和未知评估的不确定问题[14,15],在风险评估及应急管理[16-19]中得到广泛应用。鉴于此,本文将ER理论引入震后应急救援派遣模型,利用等级置信度确定救援队伍相对各受灾点的救援效率;基于时间约束构建阶段子方案,在考虑各阶段子方案关联性基础上建立多阶段动态时限优化模型,通过模型求解得到最佳派遣方案。
1 问题描述
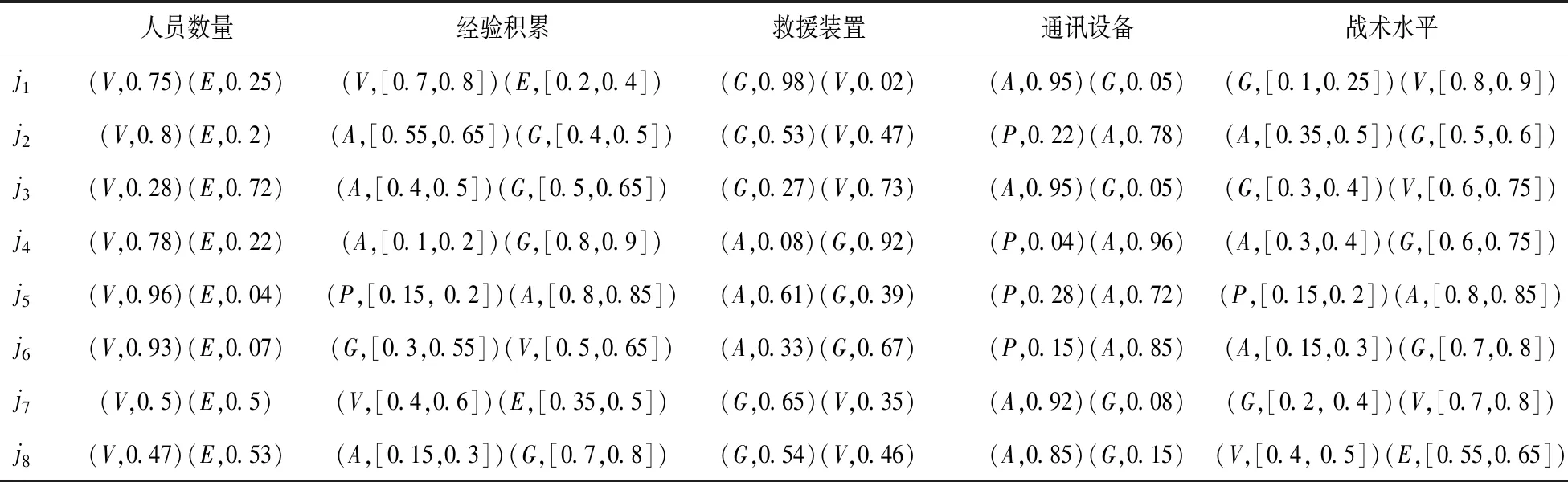
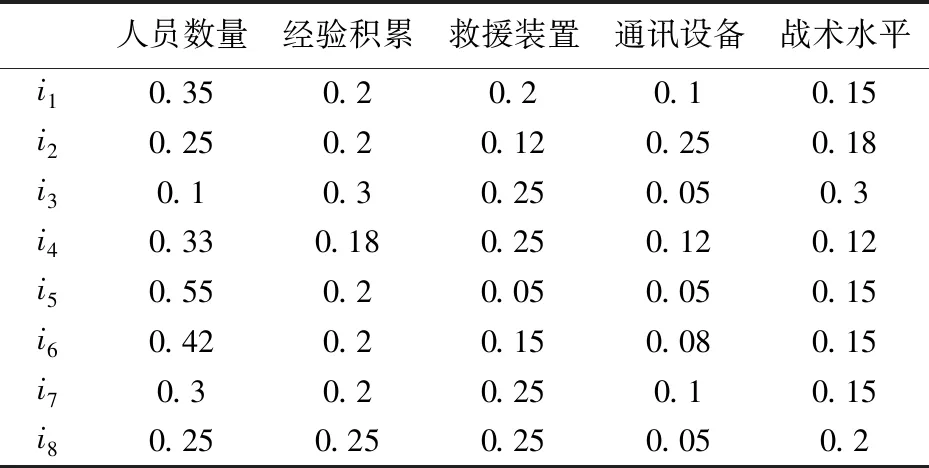
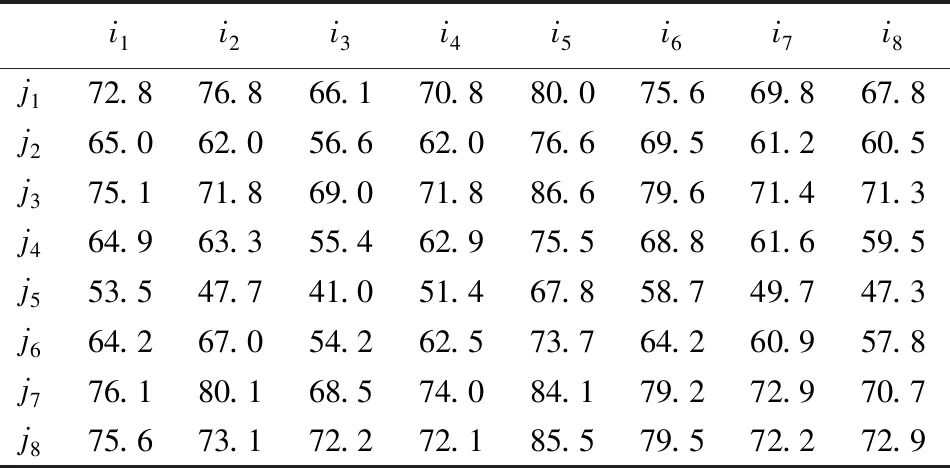
破坏性地震发生后整个救援过程分为t个阶段,t=1,2,…,l。受灾点表示为i(i=1,2,…,u),应急救援队伍表示为j(j=1,2,…,v)。震后整个应急救援过程中,救援队伍数量往往不能满足各受灾点需求,因此,只能分阶段派遣bt(bt≤v)支队伍对at(at≤u,at>bt)个受灾点进行救援。决策者依据各受灾点信息从人员数量、经验积累、救援装置、通讯设备、战术水平[20]等方面对救援队伍救援效率进行评估,通过扩展证据推理的权重维度构建效率矩阵Wij。考虑到救援的时效性,要求救援必须在dt范围内展开,而救援队伍实际到达受灾点的时间为eijt(i=1,2,…,at;j=1,2,…,bt;t=1,2,…,l),受此时间约束,本文考虑救援队伍bt 震后各受灾点由于受灾人口、受灾程度以及受灾区域等情况不尽相同,因此,决策者针对不同受灾点评估同一救援队伍时其属性权重存在明显不同,例如,人口较多但地震强度较低的受灾点对救援队伍中人员数量的权重要明显高于救援装备,而人口较少但地震强度较高的受灾点则相反。决策者可根据受灾点的初始受灾信息通过扩展证据推理的权重维度来构建救援队伍针对于受灾点的效率矩阵Wij,其中i=1,2,…,u;j=1,2,…,v。 为得到有效的救援效率矩阵,首先要对各救援队伍的人员数量、经验积累、救援装置、通讯设备、战术水平等属性(证据)进行初始评估。 对于不合理区间信度评价信息需要进行修正,具体修正方法参见WANG等[21]和WANG等[22]的研究。 由此,可将救援队伍的R个基本属性依次进行初始评估,初始评估后的信息按公式(1)-(4)转化为基本可信度形式。 n=1,…,N;r=1,…,R (1) i=1,…,u;r=1,…,R (2) r=1,…,R (3) (4) 基本可信度确定后,需要进一步将救援队伍j的R个属性进行集结,即证据合成。由于评价信息存在区间形式,所以合成后救援效率为区间形式,通过非线性优化模型确定合成后救援效率的上界及下界。 (5) (6) 其中,U(Hn)(n=1,2,…,N)为评价等级Hn的效用值。目标函数计算结果即为救援队伍j相对于每个受灾点i的区间期望效率,为便于计算,本文取区间期望效率均值构建效率矩阵Wij。 在救援效率矩阵确定后,阶段子方案主要是确定在时间约束下本阶段对哪些受灾点展开救援。针对这些受灾点,阶段子方案又包含若干派遣方案,而每一派遣方案都具有相应救援效率。因此,根据问题说明,首先应确定各阶段各子方案的最大救援效率: (17) 救援队伍必须在规定时间内到达受灾地点展开救援: max{eijtxijkt|i=1,2,…,at;j=1,2,…,bt; k=1,2,…,gt}≤dt,t=1,2,…,l (18) (19) 每支救援队伍能且只能参加一项救援任务, (20) (21) (22) (25) 针对模型特点,本文设计如下步骤对其进行求解。 Step1时间矩阵转换 Step2确定子方案 Step3子方案可行性判断与调整 2)调整。在保持每列均存在△标记前提下以时间增值最小为原则进行直接或间接调整,直至无调出行,具体调整方法参见夏少刚和刘佳[23]的研究。调整完毕后判断是否可行,若可行则转入Step4;否则继续进行调整。 Step4子方案相应最大救援效率确定 Step5重复Step1-Step4,直到确定所有阶段有效子方案及相应最大救援效率。 Step6依据式(21)判断各阶段有效子方案的动态可行性。 Step7将Step1-Step6所得数据带入模型,调用lingo程序优化确定最终派遣方案。 为验证模型有效性及演示计算过程,采用张雷和孔艳岩[12]、田玉敏[20]研究的部分数据及资料设计如下算例。假定某地发生破坏性地震灾害,灾害发生后仅本地区救援队伍远不能满足受灾点需求,需向周边地区紧急调派应急救援队伍前往灾区展开救援。整个救援过程分3个阶段向8个受灾点(i1,i2,i3,i4,i5,i6,i7,i8)派遣8支救援队伍(j1,j2,j3,j4,j5,j6,j7,j8),每支救援队只负责一个受灾点,而每个受灾点只派遣一支救援队。各阶段要求救援队分别在6小时、12小时、18小时内展开救援。第一阶段仅有4支救援队伍可派遣,第二、三阶段分别有2支队伍可派遣,各队伍到达不同受灾点耗时如表1所示,各救援队伍原始评价信息如表2所示,根据专家意见各受灾点针对救援队伍属性设定的权重如表3所示。识别框架包含P,A,G,V,E五个评价等级,每个评价等级的期望效用为:U(P)=0,U(A)=0.4,U(G)=0.6,U(V)=0.8,U(E)=1.0。现要求确定如何分阶段派遣救援队伍使其在震后规定时间范围内到达各受灾点实现整个救援效率最大。 表1 各救援队伍到达不同受灾点的时间(小时) 表2 各救援队伍原始评价信息表 表3 不同属性下各受灾点权重分布表 根据表2-表3相关信息,由式(1)-(16)可确定各救援队伍相对于受灾点的区间期望效率,为便于计算,本文取期望均值作为各救援队伍相对于各受灾地点救援效率,见表4所示。 表4 各救援队伍相对于各受灾地点救援效率(%) 在救援效率确定后,应用本文所提出方法求解上述多阶段动态时限应急救援派遣模型,主要计算过程如下: (1)第一阶段时间矩阵转换 救援第一阶段要求救援队6小时内到达受灾点,因此,转换后的时间矩阵 (2)确定子方案 (3)子方案可行性判断与调整 以第一阶段子方案1为例,进行可行性判断调整。因篇幅所限,仅列出求解结果,过程不再一一列出。经多次间接、直接调整后,结果为: 由此判断第一阶段子方案1为可行方案。 (4)确定第一阶段子方案1的相应最大救援效率 效率矩阵依可行阶段子方案1时间矩阵进行相应转化,将转化后的效率矩阵按增值最大进行调整,以寻找子方案1救援效率最大派遣方案。经多次调整后,救援派遣方案如下所示。 (5)由此,经计算可依次得到1-3阶段所有有效子方案及其相应最大救援效率,见表5所示。 表5 各阶段有效子方案及相应最大救援效率(%) 在确定各阶段救援子方案及相应最大救援效率后,根据式(21)来判断阶段子方案的动态可行性。如第一阶段共有5个子方案,其中子方案一中4支救援队(j1,j2,j3,j4)在满足各约束条件下可向4个受灾点(i1,i2,i6,i7)进行救援;第二阶段共有10个子方案,其中子方案一中2支救援队(j5,j6)在满足各约束条件下可向2个受灾点(i1,i3)进行救援。由于第一、第二两个阶段中的子方案一中均向i1派遣了救援队,显然第一阶段子方案一与第二阶段子方案一动态不可行。由此,可判断各相邻阶段子方案间的动态可行性。 根据4.1及4.2的求解结果,将其带入多阶段时限动态模型并利用Lingo 10.0编程求解,得到目标函数最优值F=557.4%,此时,y51=1,y22=1,y43=1,即第一阶段按子方案5进行派遣,第二阶段按子方案2进行派遣,第三阶段按子方案4进行派遣。各子方案下具体任务派遣值为x2151=1,x6251=1,x8351=1,x7451=1 ,x5522=1,x1622=1,x4743=1,x3843=1。即第一阶段受灾点2由救援队伍1实施救援,受灾点6由救援队伍2实施救援,受灾点8由救援队伍3实施救援,受灾点7由救援队伍4实施救援;第二阶段受灾点5由救援队伍5实施救援,受灾点1由救援队伍6实施救援;第三阶段受灾点4由救援队伍7实施救援,受灾点3由救援队伍8实施救援。 地震灾害具有突发性和难以预测性等特征,快速有效的应急救援是保证灾区群众生命安全的重要措施。本文基于救援队伍连续派遣问题,利用等级置信度确定救援队伍相对各受灾点的救援效率,考虑救援时间约束及阶段救援的动态可行性,以应急救援效率最大化为优化目标构建0-1非线性整数规划模型,并通过求解得到应急救援队伍多阶段连续派遣方案。下一步将对救援力量不足情况下考虑救援优先等级的连续动态指派问题进行研究。2 救援能力评估
2.1 证据推理基本概念
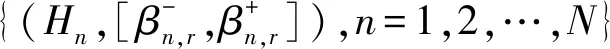
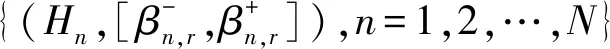
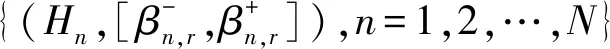
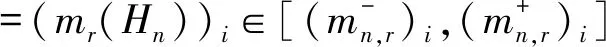
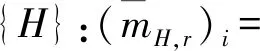
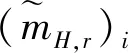
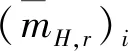
2.2 证据合成
3 模型建立与求解
3.1 基于时间约束的子方案确定
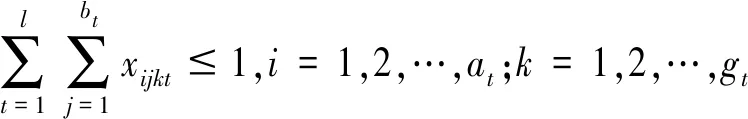
3.2 相邻阶段子方案动态可行性判断
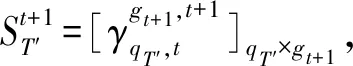
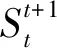
3.3 多阶段时限动态模型建立
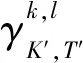
3.4 模型求解
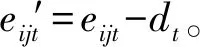
4 算例分析

4.1 确定阶段子方案及最大救援效率
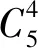
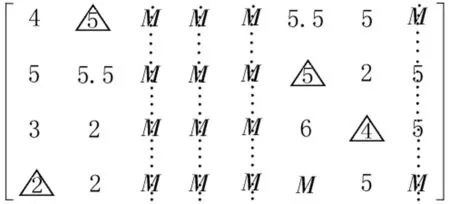
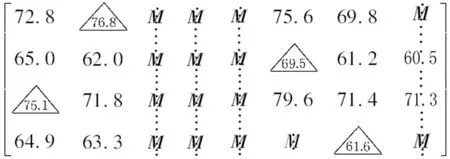
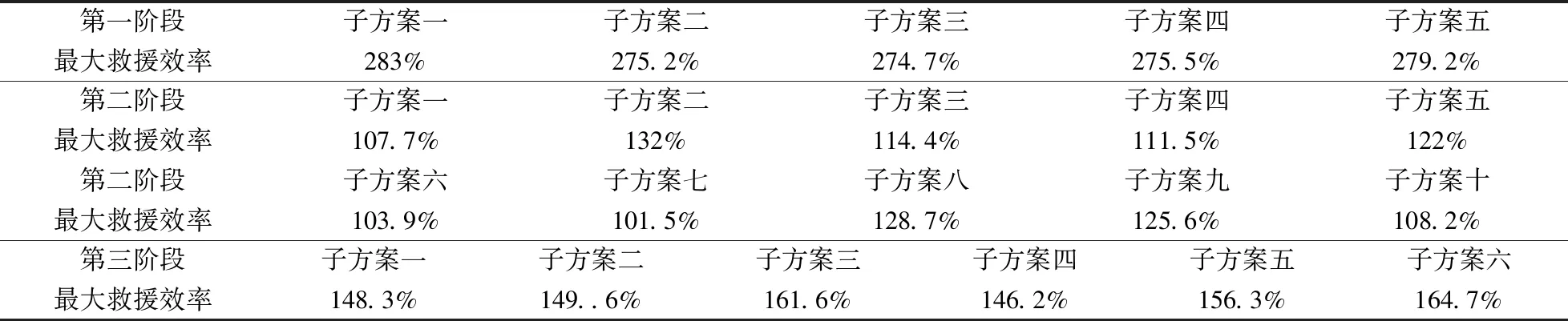
4.2 判断各阶段子方案动态可行性
4.3 多阶段时限动态模型求解
5 结论
