基于Piper-PCA-Fisher的矿井突出水源判别模型构建及应用
2023-09-25孙延辉胡文博马红林王历民李世涛
孙延辉,胡文博,马红林,王历民,杜 华,李世涛
(内蒙古上海庙矿业有限责任公司 新上海一号煤矿,内蒙古 鄂尔多斯 016200)
0 引言
由于我国煤田水文地质条件的复杂性,在煤层开采过程中极易遭受水害威胁[1-2]。尽管采取了大量防治措施,但随着开采深度的增加,煤层水压不断升高,发生突水灾害的可能性逐渐增大[3]。矿井突水水源的准确判别是开展突水防治的前提[4]。由于不同含水层水化学特征存在差异,所以通过样本水化学特征能够快速、有效地判别突水水源[5]。然而,含水层间存在极为复杂的水力联系,邻近含水层间水化学结构较为相似。因此,找到高效精准的矿井突水水源判别方法已成为当前研究的重要方向。
近年来,诸多学者利用水化学特征在突水水源判别研究上取得了一定成果。徐星等[4]将人工神经网络应用到矿井多水源识别中,认为Elman神经网络比BP神经网络更能确保全局最优性,精度更高;李垣志等[6]构建了改进的GA-BP模型,解决了传统方法对于突水水源判别存在的偶然性问题,提高了判别模型的准确性;王心义等[7]利用熵权-模糊可变集理论识别矿井突水水源,依据最大隶属度原则对样本进行归类,增强了判别模型的实用性;陈绍杰等[8]基于主成分分析及残差分析对滨海矿井水源进行了识别,研究结果为滨海地区矿井水害防治提供了科学支撑。尽管上述研究方法可以预测矿井突水水源,但评价指标间重叠性强,计算过程复杂,存在一定的误判,在样本数据有限的情况下,难以精准预测突水水源。Fisher判别法可以很好地预测小样本数据,ZHOU等[9-12]利用Fisher判别法预测了地下矿山矿柱稳定性、矿井水文地质类型、煤与瓦斯突出类型、风化基岩富水性,降低了样本数据有限的条件对预测精度的影响。但预测模型中评价指标众多且关联性强,仅采用Fisher判别法进行预测,不仅过程冗繁,预测精度也不高。
为此,笔者基于Piper-PCA-Fisher构建矿井突水水源判别模型,排除同一含水层中水化学特征存在异常的样本,提取矿井突水水源典型样本,压缩突水水源化学离子指标信息,用少量主成分代替原有评价指标,减弱化学离子间关联度,简化计算过程,确定评价集与突水水源类别距离,提高预测精度,以期在样本数据有限的情况下,得到更合理、更可靠的矿井突水水源预测结果,为矿井突水事故防治提供理论依据。
1 Piper-PCA-Fisher判别模型的构建
1.1 Piper三线图
Piper三线图是一种直观展现水样化学离子关系的方法。Piper三线图由两个等边三角形和一个菱形构成(见图1),图中左下角三角形边线表示水样中Ca2+、Mg2+、Na++K+三类阳离子的含量占比,右下角三角形表示水样中Cl-、SO42-、HCO3-三类阴离子的含量占比[13]。将菱形划分为9个部分,样本数据落在不同区域代表其具有不同的水化学特征[14]。
对于矿井中不同的含水层,水化学成分会因水文地质条件的不同而存在明显差异[15];对于矿井中的同一含水层,化学成分会通过一系列物理和化学反应保持动态平衡[16]。因此,对同一含水层水样进行分析时,会呈现相同的水化学特征,即典型样本集中于Piper三线图菱形中某一位置。为构建高精度的突水水源判别模型,应当确定典型水样,对于明显偏离大部分样本的数据,应视为异常数据而排除。

图 1 Piper三线图解
1.2 主成分分析
主成分分析本质上是一种有效的降维手段,其核心是将原始数据通过线性组合,利用矩阵正交变换将初始信息提炼,用较少主成分线性函数与特定成分之和表达原有众多指标,消除指标间的相关性,降低预测样本的复杂度,提高预测精度。分析步骤叙述如下[17-18]。
1)建立原始数据矩阵,表达式为
(1)
2)将原始数据标准化,可表示为
(2)
3)求相关系数矩阵G,表达式为
(3)
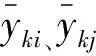
4)计算矩阵G的特征值及特征向量
|R-λIp|=0,
(4)
式中,R为计算矩阵;Ip为单位矩阵。
计算出特征值λi(i=1,2,3,…,p),按大小顺序排列后分别求出特征值对应的特征向量。
5)确定主成分数目。计算单个主成分的贡献率及主成分累计贡献率,取累计贡献率S≥85%所对应的前h个主成分。
第h个主成分的贡献率可表示为
(5)
前h个主成分累计贡献率可表示为
(6)
6)经线性组合后可得y=AX,即
(7)
1.3 Fisher判别模型

Fisher判别准则[19]表述如下。
设样本数为ni,每个样本有p项指标,协方差矩阵及均值分别为x(i)、∑(i)。为判定新样本X=(x1,x2,…,xp)T类别,构建判别函数:
(8)
式中,C=(c1,c2,…,cp)T,X=(x1,x2,…,xp)T。

(9)

最大离差比γ可表示为
(10)

根据极值存在的必要条件,经代数计算,可构造t个判别函数(t为E-1B非零特征值个数)。
单个判别函数的判别能力定义为
(11)
式中,λ为E-1B对应的特征值。
前h个判别函数的判别能力定义为
(12)
若Ps≥85%,可采用前h个判别函数进行判别。将新样本p项指标函数代入判别函数中即可求出y值,将其与判别中心值进行比较,即可判定该样本所属类别。
1.4 Piper-PCA-Fisher判别模型
运用Piper三线图将异常数据剔除,得到典型水样,以此为训练样本;利用主成分分析对判别指标进行信息提炼;将经Piper三线图剔除及主成分分析后的新训练样本输入Fisher判别中进行训练,以提高小样本数据的预测效率和精度。Piper-PCA-Fisher判别模型技术路线见图2。

图 2 Piper-PCA-Fisher判别模型技术路线
2 研究区概况
临涣矿区建于1977年,位于安徽省淮北市濉溪县韩村镇境内。该地区属暖温带半湿润气候,年平均气温14.1 ℃,年平均地表温度12.6 ℃,年平均降雨量830 mm。该区域地质构造条件复杂,存在断层、褶皱、次级褶曲等构造,且多为近东西向和北北东向[20]。流经该区域的地表水系主要是浍河,为中型季节性河流。根据地层的岩性、厚度以及区域富水条件,煤田内的含水层由上而下主要有:松散层孔隙含水层、煤系地层砂岩裂隙含水层、太原组灰岩岩溶裂隙含水层、奥陶系灰岩含水层[14,21]。
3 Piper-PCA-Fisher判别模型的应用
3.1 数据选取
根据临涣矿区水文地质资料,结合刘鑫[14]的研究成果,临涣矿区的主要突水水源类型为:来源于松散层孔隙含水层的四含水(Ⅰ类)、来源于煤系地层砂岩裂隙含水层的煤系水(Ⅱ类)、来源于太原组灰岩岩溶裂隙含水层的太灰水(Ⅲ类)以及来源于奥陶系灰岩含水层的奥灰水(Ⅳ类)。将Ca2+(X1)、Mg2+(X2)、Na++K+(X3)、Cl-(X4)、SO42-(X5)、HCO3-(X6)6类离子实测浓度作为判别突水水源类别的指标。从4类水源中选取58组实测数据进行训练与测试,具体水样数据特征见表1、表2。

表 1 临涣矿区水样数据(训练集)

表 2 临涣矿区水样数据(测试集)
3.2 典型水样筛选
为确定典型水样,将表1中43组训练样本按类别绘制四含水、煤系水、太灰水、奥灰水的Piper三线图。其中,由于四含水和奥灰水训练样本较少,将测试样本中四含水、奥灰水数据加入对应类别绘制。4类突水水源Piper三线图见图3。
由图3(a)可知:四含水主要分布在4区,即强酸大于弱酸区,阳离子以Na+为主,阴离子中Cl-占比较大:5号水样明显远离其他样本,故将其作为异常样本剔除。由图3(b)可知:煤系水中9、14、20号水样明显远离其他样本,故将其作为异常样本剔除;其余12组样本筛选为煤系水典型水样,主要分布在8区,即以碱土金属离子及弱酸为主;煤系水中Na+占阳离子的80%以上,阴离子中HCO3-质量浓度远高于Cl-和SO42-,表明煤系水的主要化学类型为Na-HCO3。由图3(c)可知:太灰水主要分布在9区,主要化学类型为Ca-Mg-Cl-SO4;23、34号样本与其他样本相距较远,故将其作为异常样本剔除。由图3(d)可知,7组样本分布散乱,无规律可循,因此该水样类别不剔除异常样本。
综上所述,将表1中5、9、14、20、23、34号样本作为异常样本剔除,确定其余37组数据作为突水水源典型样本,用于下一步的水源判别模型训练。
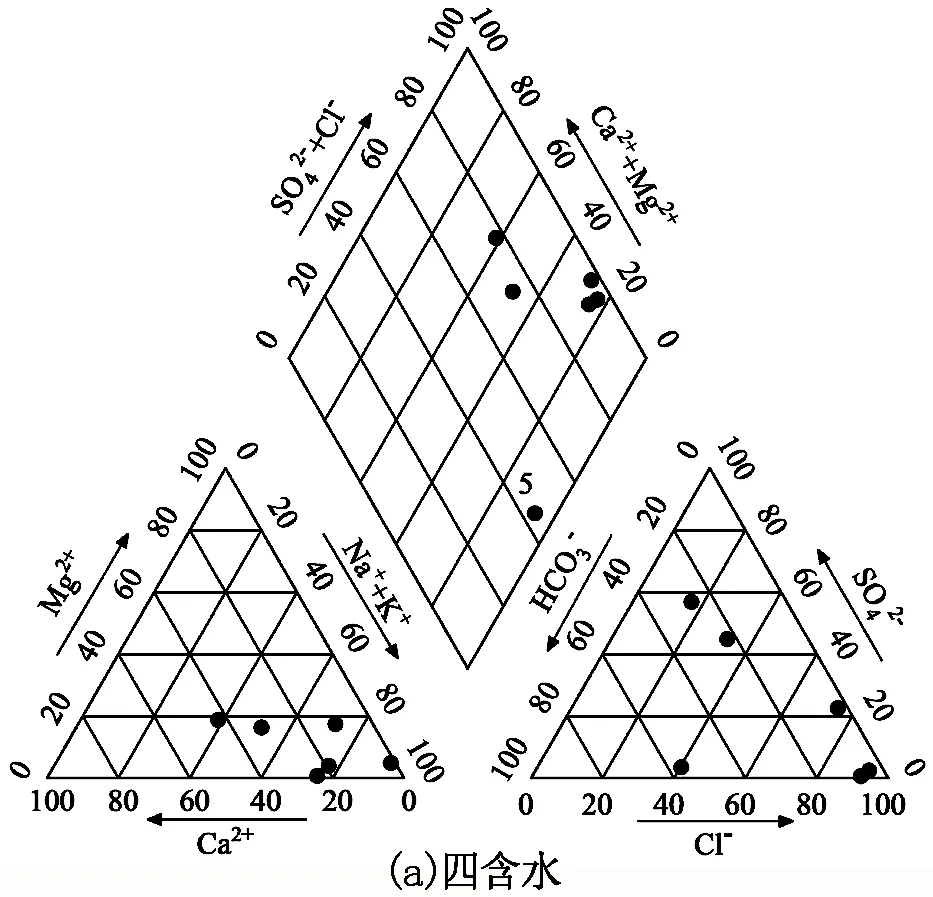
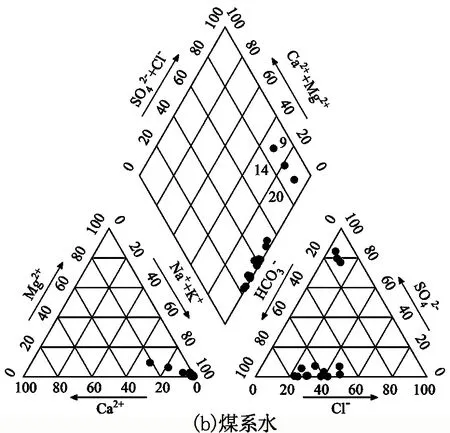


图3 水样Piper三线图
3.3 主成分分析
利用SPSS(Statistical Product and Service Solutions)软件对表1中剔除异常数据后的37组数据及表2中的15组数据的6项评价指标作标准化处理后进行主成分分析,由此得出矿井突水水源各主成分的特征值及其贡献率(见表3);突水水源PCA碎石特征值及累计贡献率见图4。由表3可知,前3项主成分的累计贡献率为91.636%,说明前3项主成分包含原有指标数据91.636%的信息。由图4可知,前3个主成分特征值散点图呈陡坡形,后3个主成分特征散点图趋于平缓,表明前3项主成分可以较好地解释原始指标的绝大部分信息,且各成分间的重叠性弱。因此,提取前3项主成分代替原有的6项离子信息,可以较为完整地表征样本水化学特征。

表3 突水水源主成分特征值及其贡献率

图4 突水水源PCA碎石特征值及累计贡献率
利用SPSS软件求得突水水源3个主成分的因子载荷矩阵(见表4)。其中,第1主成分Y1与Ca2+、Mg2+、HCO3-三类离子显著相关,表明Y1包含Ca2+、Mg2+、HCO3-的指标信息。同样可以确定,第2主成分Y2包含Na++K+的指标信息;第3主成分Y3包含Cl-、SO42-的指标信息。

表4 突水水源主成分矩阵
在确定3个主成分后,结合主成分系数矩阵,得到主成分与标准化原始变量的数学关系式[见式(13)-式(15)]。
Y1=0.298X1+0.281X2-0.159X3
+0.141X4+0.248X5-0.256,
(13)
Y2=0.167X1+0.125X2+0.532X3
+0.405X4+0.125X5+0.345X6,
(14)
Y3=-0.165X1+0.270X2+0.168X3
-0.657X4+0.643X5+0.260X6。
(15)
3.4 突水水源判别
基于主成分分析将提取的3个主成分即Y1-Y3作为Fisher判别指标输入层,将筛选后的37组数据作为训练样本输入、15组测试数据作为预测样本输出,输出参数为水源类别。利用SPSS软件,由Fisher判别法算得突水水源判别函数[见式(16)-式(18)]。判别函数特征值见表5。
Z1=5.390Y1+0.981Y2-0.868Y3-0.338,
(16)
Z2=-0.158Y1+2.206Y2+0.130Y3-0.107,
(17)
Z3=0.114Y1-0.071Y2+0.841Y3-0.023。
(18)
由表5可知:判别函数Z1对应的特征值为33.184,典型相关性达到0.985,Z2对应的特征值为3.474,典型相关性达到0.881;这2个判别函数的相关性均大于0.85,证明其判别能力显著;且累计方差为100.00%,表明运用函数Z1、Z2即可判别样本的全部信息。

表 5 判别函数特征值
利用SPSS软件得到水源判别中心值(见表6)。通过比较预测样本函数值与水源判别中心值的距离,确定样本最终突水水源。测试样本判别结果见表7。
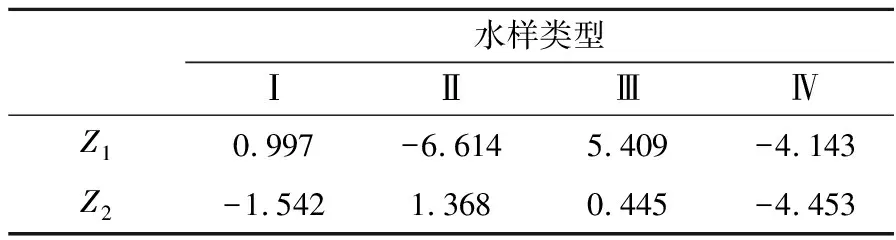
表 6 4类水源中心值

表7 预测样本判别函数值及判别结果
为检验Piper-PCA-Fisher判别模型的准确性及可靠性,将37组训练样本数据逐一回判。为了更加直观地展现评价结果,将37组训练样本及15组预测样本判别结果绘制成离散点图(见图5)。
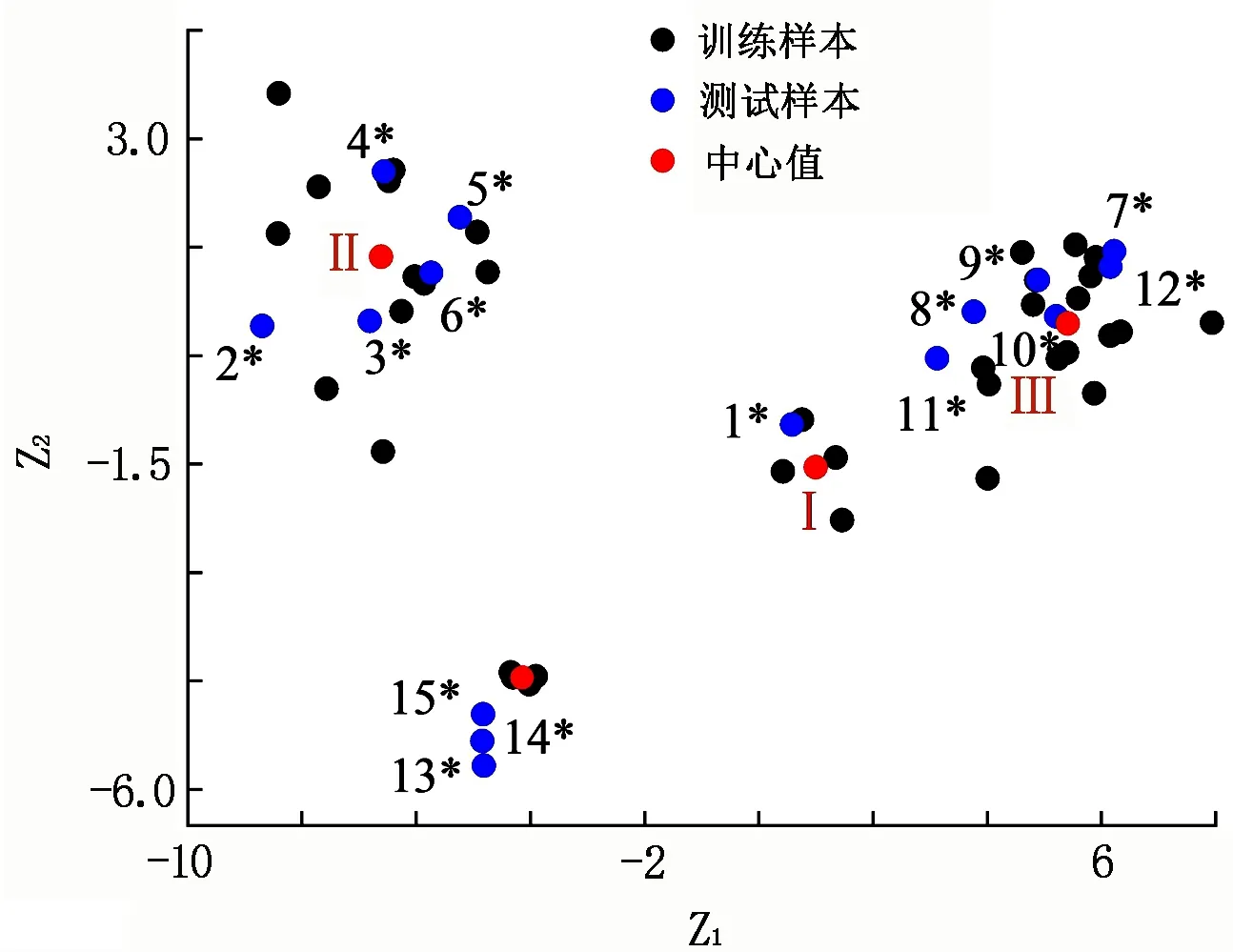
图 5 样本水源类别判别离散点图
由表7及图5可知:Piper-PCA-Fisher判别模型对突水水源的37组训练样本回判正确,15组预测样本判别结果全部正确,预测及回判过程中没有造成误判。由此可见,Piper-PCA-Fisher判别模型能满足突水水源判别的实际要求,且简单易行、准确性高。
4 结论
a.同一含水层样本水化学特征相同,通过Piper三线图剔除同一含水层中水化学特征存在异常的样本,确定典型水样作为训练样本,以提高判别模型的可靠性。
b.采用主成分分析对影响水源类别的化学指标进行降维、净化处理,确定3个主成分代替原有的6项离子信息,可降低水样化学离子间的关联度,提高预测精度。
c.将确定的3个主成分代入Fisher判别模型中,对15组预测样本数据进行预测,并对37组典型水样逐一回判,误判率均为0,与实际类型一致。
d.矿井突水水源的Piper-PCA-Fisher判别模型具有较高的稳定性,且简单易行、准确性高。
