风电机组两分段下垂调频控制策略及参数整定方法

2023-09-25高海淑

电力系统自动化 2023年18期

高海淑，张峰，丁磊

（电网智能化调度与控制教育部重点实验室（山东大学），山东省济南市 250061）

0 引言

新型电力系统建设背景下，高比例新能源将进一步接入电网［1］，大量电力电子设备与电网之间的解耦特性使得系统惯量水平显著降低［2］，加剧了扰动发生时的频率失稳风险。因此，具有高自由度控制特性的新能源参与系统调频成为必然趋势［3］。

风电机组参与系统调频的能量支撑主要来源于功率备用［4-5］和桨叶动能［6-7］，前者通过释放风机中的预留功率，后者通过暂时释放风机存储的桨叶机械动能，来提供短时功率支撑。相比而言，采用桨叶动能可使风电机组避免长期工作在减载状态，具有更好的经济性［8-9］。当电网发生功率扰动时，通过降低转速释放桨叶机械动能来参与调频，能够抑制扰动后短期内的频率跌落。因此，本文以桨叶动能为调频能量来源，构建调频策略。

风电机组利用桨叶动能参与系统调频的常见控制策略包括：下垂控制［10-12］、虚拟惯量控制［13-15］以及两者结合的综合惯量控制［16-19］。虚拟惯量控制通过频率变化率（rate of change of frequency， ROCOF）提供功率支撑。下垂控制响应功率与频率偏差成正比，在扰动初始阶段的贡献有限，但能有效减小频率下跌的幅度。综合惯量控制包含下垂控制与虚拟惯量控制，是最常用的风电机组调频控制策略，具有与传统同步机相似的调频模式。

然而，风电机组虚拟惯量的本质是快速功率响应，与同步机零延迟惯量响应具有本质区别［20-21］。虚拟惯量存在测频时间长、弱电网接入下测频精度不高、微分环节有误差放大作用等问题［22-23］，适应能力相对较弱，严重影响了虚拟惯量控制的调频效果。相比而言，基于频率偏移量的下垂控制受测量精度等影响较小，适应能力强，适合复杂场景下的可靠调频控制［24-25］。

为解决传统虚拟惯量调频可靠性偏低的问题，本文提出了两分段下垂控制的风电机组调频策略。通过对下垂系数进行分段处理，在第1 时段增大下垂系数，保障调频效果；第2 时段减小下垂系数，保障不增加能量需求，最终达到替代综合惯量的目的。具体而言，首先，建立频率响应时域解析模型，采用分部积分法对该模型进行合理化简，求得两分段下垂控制与综合惯量控制的频率响应解析解。然后，量化频率最低点与调频能量的解析表达式，根据解析表达式，对两分段下垂控制与综合惯量控制进行对比分析，得到前者能够对后者进行替代的结论；进一步，将两个时段的下垂系数与分段时间作为可控的替代参数，并针对替代参数选取困难的问题，提出整定两分段下垂调频参数的方法，并给出了参数在线应用策略。最后，仿真验证了所提策略及调频参数整定方法，不仅能够替代综合惯量，而且具有更好的调频效果。

1 系统频率响应模型解析

通过在传统系统频率响应（system frequency response，SFR）模型的基础上加入风电机组的功率控制环节，建立了如图1 所示的风电渗透率为p的动态SFR 模型，并基于该模型对频率响应进行解析。图中：ΔPL（t）为功率扰动；s为复数变量；FH为汽轮机高压缸做功比例；TR为再热器时间常数；R为同步机调差系数；M为同步机惯性时间常数；D为同步机阻尼系数；为同步机机械功率变化量；为风电机组调频期间功率变化量；GWe（s）为风机调频功率与频率之间的关系式；Δf为实际频率与额定频率fn的差值。在风机参与调频的时间尺度内，认为同步机开停机计划不变、风速不变［26］、负荷相对固定［27］，系统在频率动态时间尺度下可近似为定常系统。

图1 系统频率动态响应模型Fig.1 Dynamic response model of system frequency

1.1 综合惯量频率响应模型解析

风电机组以综合惯量控制参与调频时，利用GWe（s）环节进行表达：

式中：kp为风电机组调频的下垂系数；kd为风电机组的虚拟惯量系数。

考虑到文中后续所提的分段调频控制中，无法建立传统的复数域模型进行分析。为此，本节建立系统频率的时域解析模型，并重点对时域模型中存在的冲激函数项进行分析，最终求取频率控制模型的时域解析表达式。

根据图1，建立综合惯量控制的系统频率时域解析模型如下：

式中：a1～a4为系数；Δf(t)为综合惯量控制下的系统频率；Δf˙(t)和Δf¨ (t)分别为频率的一阶和二阶导数；ΔP˙L(t)为功率扰动的一阶导数。

设扰动功率为阶跃函数ΔPL（t）=u（t）ΔPL，其中u（t）为单位阶跃函数，ΔPL为扰动大小。求解微分方程的解析解可表示为：

式中：C1、C2为常系数；λ1、λ2为齐次方程对应的特征根；a5为系数；X为变量。

由于式（2）等式右边存在阶跃函数的导数，即冲激函数，等式左边Δf¨ (t)项要有冲激项来保证等式成立，由此可得Δf˙(t)含有t=0 时刻的阶跃项。为了求解频率一阶导数在t=0+时刻的值Δf˙(0+)，对式（2）两边分别在区间[0-，0+]进行积分。化简得到：

考虑到频率不能发生突变，频率在t=0+时刻的取值Δf(0+)=0，将式（5）代入式（4），得到常系数C1、C2表达式如式（6）所示，其中，a6为系数。

由此得到综合惯量控制的频率响应解析表达式为：

1.2 两分段下垂频率响应模型解析

为实现对综合惯量的替代，提出两分段下垂控制策略。但两分段下垂调频控制机理未见相关研究，频率响应模型难以解析。其难点在于下垂系数在分段点处发生突变，与1.1 节中功率扰动引入的冲激响应相比，下垂系数的突变不仅导致第2 阶段频率响应为非零初始响应，而且初始值均为变量，增加了分段点处初始条件的求解难度，使频率响应表达式变得异常复杂。

为此，本节采用如下步骤开展两分段下垂控制的频率响应模型解析：首先，构建两分段调频解析模型，获得第1 时段频率响应解析解；然后，对分段时刻t=td处，单独建立时域解析模型，并采用分部积分法对该模型进行展开，重点对含有冲激函数乘积的积分项进行合理消减，得到与调频参数相耦合的第2 时段非零初始条件。由此，求解得到全时段频率响应解析表达式。

当风电机组采用两分段下垂控制策略参与辅助调频时，两分段下垂系数可表示为：

系统频率时域解析模型可表示为：

式中：Δf″(t)为两分段下垂控制下系统频率响应解析表达式，分别为该频率响应的一阶、二阶导数；为两分段下垂系数的一阶导数。

第1 时段下垂控制的频率响应解析式参考1.1节综合惯量控制频率解析表达式（7）。当kd=0 时，可得第1 时段下垂控制的频率解析表达式为：

第2 时段［td，T］频率响应的频率解析表达式为：

列写t=td时刻的频率时域解析模型，并将其在区间[td-，td+]进行积分，化简得到：

对比式（14）与式（15）可看出，式（14）中所包含的冲激函数与函数乘积的积分项，恰好可以与分部积分法展开后得到的积分项相抵消。进一步，将式（15）代入式（14），化简后便可得到另一个初始条件，可表示为：

将两个初始条件式（13）和式（16）代入式（12），得到常系数的表达式（见附录A 式（A1）、式（A2））。由此，可得到第2 时段频率响应表达式（见附录A 式（A3）），并最终获取两分段下垂的频率响应解析表达式（见附录A 式（A4））。

2 基于模型解析的两分段下垂控制替代能力分析

为了保证两分段下垂替代后的系统频率最低点不低于综合惯量控制，第1 时段的下垂系数需要满足＞kp，而下垂系数的增大会进一步增加调频能量需求。为保证替代后不增加调频能量，第2 时段的下垂系数需要满足＜kp。基于此，本章首先根据频率响应解析表达式，量化频率最低点与调频所需能量，进一步证明在相同调频能量下，以频率最低点为指标，两分段下垂控制对综合惯量控制具有可替代性。

2.1 频率最低点解析求解

对频率响应表达式（7）求导，其数值为零时，对应综合惯量控制下的频率最低点发生时刻tm，其表达式如式（17）所示，其中，a7为系数。

将式（17）代入式（7），经过整理简化后可得综合惯量控制下频率最低点Δfmin的解析表达式，如式（18）所示。

由附录A 式（A4）的两分段下垂频率响应解析模型可知，在负扰动下，两分段下垂控制的频率最低点可表示为：

基于附录A 式（A4），求解两分段下垂控制两个时段的频率到达最低点的时间及频率的最低点，分别由式（20）至式（22）与附录A 式（A5）表示。

2.2 风机调频能量解析求解

风电机组参与调频的能量可由风机调频期间的功率增量对调频时间的积分计算得到［16］。其中，以综合惯量控制参与调频时，其释放能量W为：

将式（7）代入式（23），化简可得：

风电机组以两分段下垂控制参与调频时，释放的能量W″可表示为：

将附录A 式（A4）代入式（25），化简得到两分段下垂控制释放的能量如式（A6）所示。

2.3 相同调频能量下两分段下垂控制的替代能力分析

本节以频率最低点表达式（式（18）、式（21）与附录A 式（A5））与调频能量表达式（式（24）与式（A6））为模型基础，论证当综合惯量控制（调频参数kd和kp）与两分段下垂控制（调频参数、td和）的调频能量相同时，通过合理设置两分段下垂控制调频参数，使后者具备替代前者的能力。

首先，建立能量描述方程。由式（24）、附录A式（A6）可知，对于某电力系统，风机参与调频的能量与随机变量ΔPL及可控变量调频参数有关。能量可描述为：

对式（24）、附录A 式（A6）进一步分析可发现，W与W″均与ΔPL呈线性关系。因此，能量描述方程可进一步化简为：

然后，在能量描述方程下，基于频率最低点表达式（式（18）、式（21）与附录A 式（A5）），分析两分段下垂与综合惯量控制的频率最大偏差。为便于分析，采用典型系统参数：FH=0.3，TR=10，R=0.05，M=10，D= 1，p=0.3［28］，设系统基本频率fn为50 Hz。考虑到锅炉热量转换到同步机机械转矩的时间，即一次调频响应到位的时间一般在30 s 左右［12］，设定风电机组参与调频时间T=30 s，以功率扰动ΔPL=-0.1 p.u.，且风机以综合惯量控制（kd=10，kp=10）参与调频时所释放的能量W0为例进行分析。

图2 、td与频率最大偏差三维图Fig.2 Three-dimensional diagram of , td and frequency maximum deviation

由图2 可以看出，曲面图的大部分处在平面图的下方，即两分段下垂控制的频率最大偏差大部分情况均小于综合惯量控制。同时，在过大、过小或td过大、过小时，两分段下垂控制的频率最大偏差可能会大于综合惯量控制。原因在于：td取值确定后，若过小，0 ＜t≤td时段的功率支撑不够，会导致第1 时段频率最大偏差较大；若过大，在能量约束下，t＞td时段的可调能量较少，导致第2 时段频率最大偏差较大。同理，取值确定后，若td过小，频率来不及恢复就出现第2 次跌落，从而导致较大；而若td过大，会导致t＞td时段内可调能量过少，的取值过小，也会导致较大。

综上所述，在能量描述方程下，相比于综合惯量控制的下垂系数kp，设置两分段下垂调频参数，大约在区间［kp+5，kp+15］。td大约在5～15 s 区间时，两分段下垂控制的频率最大偏差均小于综合惯量控制。由此，在以频率最低点为替代指标下，前者具备替代后者的能力。

与此同时，由图2 可以看出，在上述参数范围内，选取综合惯量频率最大偏差平面图下方的曲面中任意点对应的参数组合，均可作为替代综合惯量的两分段下垂调频参数。但是，如何选择作为替代的调频参数缺乏统一标准，因此，下文将研究满足替代条件的两分段下垂调频参数的具体整定方法。

3 基于频率解析表达的两分段下垂调频参数整定

基于式（19），对于任意系统参数与任意综合惯量调频参数，在能量描述方程式（27）的约束下，两分段下垂的频率最大偏差关于可控变量一定存在极值点。而由图2 可以看出，频率最大偏差|存在极小值，且只有一组两分段下垂调频参数与之对应。另外，由2.3 节可知，| 的极小值也一定满足替代条件|，并且可以最大限度地提高频率最低点，实现更好的替代效果。为此，将满足频率最大偏差|的极小值作为调频参数的选择标准，通过寻找的极小值所对应的调频参数，来确定替代后的两分段下垂调频参数，并将该参数称为最优调频参数。

由上文分析可知，穷举法随着系统参数的变化，需要重新穷举计算，且极值精度受数组步长影响较大，同时伴随参数区间变化等问题，缺乏实用性。而通过解析表达式计算|极值点的方法，由于频率响应表达式过于复杂，直接利用解析表达式求解将会产生超越方程，无法进行直接求解。为此，本文将两分段下垂调频参数的整定视为一个以提高频率最低点为目标的优化问题，通过优化求解，获取|极小值所对应的最优调频参数。

优化模型以频率最大偏差的极小值为目标函数，以式（27）所示的能量描述方程为约束条件，并基于式（21）与附录A 式（A5），参数整定优化模型可表示为式（28）。

式中：min_ming表示两分段下垂控制下，频率最大偏差的极小值，也是最小值，其是控制变量、td和的函数。

所提调频参数整定方法采用离线方式应用于实际风电场。若风电场采用综合惯量控制策略参与调频，则可依据风电场所提供的综合惯量调频参数，根据式（28）进行参数整定，得到两分段下垂调频参数；若风电场为新增风电场或不采用综合惯量控制策略，则可根据风电场实际可用调频能量W，采用N-1 校验，建立能量约束方程W=W″，结合式（28）建立优化模型，进一步整定得到两分段下垂调频参数。

整定得到的两分段下垂调频参数为系统层面单机等值后的参数。为了将参数映射到场站或单机，首先，将调频参数根据各风电场调频能量占比进行比例分配；然后，风电场根据所分配的调频参数，依据风电场内每台机组的运行工况，将调频参数或功率参考值下发到风电机组，控制风机参与调频。

4 算例分析

为了验证SFR 模型解析求解的正确性与所提策略及其参数整定方法的有效性，在MATLAB/Simulink 中搭建了如附录B 图B1 所示的包含风电机组与同步机的两区域系统频率动态响应模型进行仿真分析。

设定风电场额定功率为30 MW，系统初始有功负荷为97 MW，风机正常运行时的转子转速为1.2 p.u.，系统基准频率为50 Hz。系统在t=40 s 时负荷突增5 MW，风机参与调频的时间T为30 s，仿真时间为100 s。其中，风机速度控制器比例系数Kpt与积分系数Kit正常运行时分别为3 与0.6。为了保证风机调频过程中实际调频转矩增量，设置两个系数在调频期间均为0。此外，为了减缓风机退出调频后的频率跌落速度，在风机退出调频后，设置Kpt和Kit在20 s 内由0 分别线性增加到3 和0.6。仿真模型中，同步机与风机其余相关参数如附录B 表B1 与表B2 所示。粒子群智能算法的参数设置为：粒子群种群规模为150，迭代20 次，个体学习因子和群体学习因子分别为2 和1.5。

4.1 低电压场景下的调频效果分析

风机参与调频主要通过附加功率环节对系统提供频率支撑，频率偏差与频率变化率需要由差值与微分环节测量得到。为了分析下垂控制与虚拟惯量控制的调频功率支撑效果，基于附录B 图B1 所示的两区域模型进行仿真分析。综合惯量控制的调频参数为kd=10，kp=10，仿真结果如附录B 图B2 所示。由图B2 可看出，大功率扰动下，电压支撑能力不足的并网点的系统频率可能发生明显波动。此时，通过微分环节的虚拟惯量控制，微分环节放大了测量误差，导致输出功率波动幅度较大，甚至出现负向功率支撑。相比而言，下垂控制的波动较小，可靠性较高。

为考虑一般性，充分明确所提方法的适用范围，后文将基于常规并网点电压波动场景进行有效性验证。

4.2 SFR 模型解析解的有效性验证

为了验证频率响应解析解的正确性，风电机组分别以综合惯量控制与两分段下垂控制参与系统调频，将解析式（7）、附录A 式（A4）、式（17）至式（22）及式（A5）计算得到的系统频率响应结果，与Simulink 搭建的图1 所示SFR 模型仿真结果进行对比。其中，综合控制系数kd和kp均为10，两分段下垂控制系数设为：=15，td=10，=7，其余参数与2.3 节一致。通过模型仿真得到的结果与解析求解得到的结果如表1 与附录B 图B3 所示。

表1 系统频率响应的仿真与解析结果对比Table 1 Comparison of simulation and analytical results of system frequency response

由表1 与附录B 图B3 可以看出，仿真得到的频率响应结果与解析求解得到的结果具有一致性，验证了综合惯量控制与两分段下垂控制解析解的正确性。

4.3 两分段下垂调频策略及参数整定方法的有效性验证

从两个方面对两分段下垂调频策略及参数整定方法进行有效性验证，仿真模型采用附录B 图B1 所示的两区域系统。首先，从调频效果上验证所提策略及参数整定方法相对于综合惯量控制的优越性；然后，通过改变随机变量的大小（负荷扰动、综合惯量调频参数），根据第3 章所提参数整定方法，采用粒子群算法，整定得到相对应的两分段下垂调频参数，以此进行仿真分析，验证所提策略及整定方法应对不同大小的负荷扰动及综合惯量调频参数的可行性。

4.3.1 调频效果的有效性验证

给定综合惯量控制的调频参数为kd=10，kp=15，设置系统在t=40 s 时负荷突增5 MW。根据第3 章所提参数整定方法，采用粒子群算法，整定得到两分段下垂控制的最优调频参数（、td，best、分别为26.106 6、9.405 9、10.071 2），两种调频策略下的频率响应仿真结果对比如图3 与表2所示。

表2 两分段下垂与综合惯量的调频效果对比Table 2 Comparison of frequency regulation effect between two-segment droop and integrated inertia control

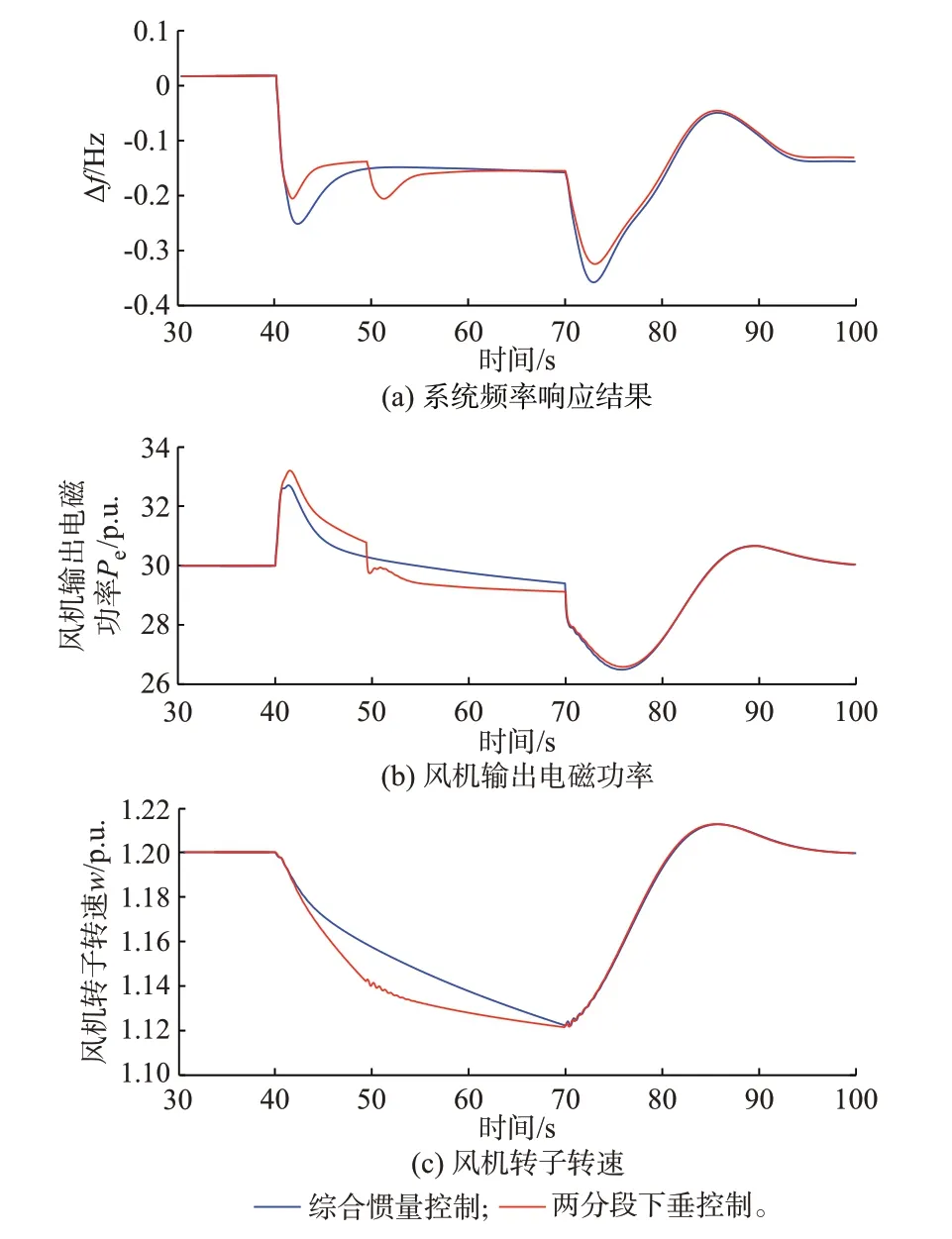
图3 两分段下垂与综合惯量控制频率响应结果对比Fig.3 Comparison of frequency response results between two-segment droop and integrated inertia control

由图3（c）可以看出，综合惯量控制下，转子转速在虚拟惯量支撑期间跌落较快。频率恢复阶段，转速基本处于匀速下降状态，而两分段下垂控制由于在调频第1 时段增大下垂系数、调频第2 时段减小下垂系数，故其在第1 时段转子转速下降较快，在第2 时段下降较慢，最终在风电机组退出调频时，两种控制策略下的风电机组转速基本一致。因此，可看作两种策略参与调频所释放的桨叶动能基本一致。

由图3（a）与表2 可以看出，在两种调频策略所释放的能量基本一致的情况下，相比于综合惯量控制，本文所提两分段下垂控制策略及参数整定方法能够大幅提高频率最低点，并且调频后期下垂系数的减小还能缓解频率二次跌落。这是因为在调频后期减小下垂系数可减小风机辅助调频功率，从而充分利用了同步机一次调频的功率支撑作用，相当于在风电机组退出调频时，减小了系统的功率扰动，故可以减缓由于风电机组退出而导致的频率二次跌落。

对比图3（a）和（b）可知，在扰动发生瞬间，虚拟惯量控制受ROCOF 的影响，在瞬间释放有功功率，减缓了频率下跌速度。而两分段下垂控制虽无虚拟惯量的支撑作用，但缩短了频率跌落的时间。因此，能较快地释放功率支撑。此外，两分段下垂控制在调频第1 时段增大下垂系数，增加了功率输出量，最终实现了提高频率最低点的目的。

4.3.2 应对不同随机变量的可行性验证

本节通过给定不同大小的综合惯量控制参数与负荷扰动，并采用附录B 图B1 所示模型进行仿真对比，验证所提策略及整定方法应对不同大小的负荷扰动及综合惯量调频参数的可行性。

首先设置两个仿真场景：

场景1：系统在t=40 s 时负荷突增5 MW，并给定4 组大小不同的综合惯量控制参数；

场景2：综合惯量控制的调频参数为kd=10，kp=15，并给定3 组大小不同的负荷扰动值，且均设为负荷增加。

根据各场景下的每组参数，整定得到两分段下垂调频参数如表3 与表4 所示。最后，对表中的调频参数进行仿真验证，仿真结果如表5、表6、图4 与图5 所示。

表3 不同综合惯量控制参数下的仿真参数Table 3 Simulation parameters with different integrated inertia control parameters

表4 不同负荷扰动下的仿真参数Table 4 Simulation parameters under different load perturbations

表5 不同综合惯量控制参数下的仿真结果Table 5 Simulation results with different integrated inertia control parameters

表6 不同负荷扰动下的仿真结果Table 6 Simulation results under different load perturbations

图4 不同综合惯量控制参数下的频率响应Fig.4 Frequency response with different integrated inertia control parameters

图5 不同负荷扰动下的频率响应Fig.5 Frequency response under different load perturbations

对比表3 和表4 中两分段下垂控制的分段时间td，best可以发现，在不同综合惯量参数及不同负荷突增值下，分段时刻变化较小，基本在9～10 s 之间，即分段时刻受综合惯量控制参数与负荷扰动的影响较小。

由表4 可以看出，在不同扰动下，两分段下垂的调频参数基本相同，即两分段下垂的调频参数大小与负荷扰动大小无关。这是因为，受能量约束的影响与|大小呈负相关，若要满足在能量一定的条件下系统频率最大偏差最小，则须满足|。因此，两分段下垂调频参数的整定可以视为：在方程与式（27）能量方程的约束下，求的最大值（即频率偏差最小）的问题。该参数整定的过程与ΔPL无关。因此，两分段下垂调频参数大小也与负荷扰动大小无关。

由图4 和表5 可以看出，对于具有不同调频参数的综合惯量控制，两分段下垂控制能在不增加调频能量的条件下，有效提高频率最低点，并缓解风机退出调频时的频率二次跌落，具有更优的调频效果。此外，由图5 与表6 可以看出，两分段下垂控制参数的大小与系统扰动大小无关。在不同大小扰动下，两分段下垂控制均具有较好的调频效果。因此，两分段下垂控制策略及参数整定方法能够很好地应对系统中不同大小的扰动，验证了本文所提调频策略及参数整定方法在不同综合惯量控制参数、不同扰动下均具有较强的适应性。