基于机会约束规划的配电网分布式光伏承载力提升方法

王强强，姚良忠，盛万兴，徐业琰，刘科研，程 帆

（1.武汉大学电气与自动化学院，湖北省 武汉市 430072；2.交直流智能配电网湖北省工程中心（武汉大学），湖北省 武汉市 430072；3.中国电力科学研究院有限公司，北京市 100192）

0 引言

在国家“双碳”目标和整县光伏开发的背景下，分布式光伏密集接入是未来配电网一种新的结构形态。大量分布式光伏接入改变了配电网潮流分布，增加了配电网电压越限风险［1］。此外，分布式光伏出力的不确定性为配电网规划运行带来了新的挑战［2-3］。因此，亟须开展不确定性下考虑安全运行约束的配电网分布式光伏承载力研究。

分布式光伏承载力通常是指在满足安全运行约束下能够接入的分布式光伏最大容量［4］。也有文献采用“准入容量”或“接纳能力”来描述［5-6］。限制分布式光伏接入的约束条件有电压安全约束［7］、线路容量约束［8］、谐波束［9-10］、继电保护约束［11-12］以及频率稳定约束［13］等。其中，电压安全约束是最关键的制约因素［14-15］。分布式光伏承载力计算的本质是一个优化问题。文献［16］提出计及多约束的多分布式电源承载力评估优化方法，但未考虑不确定性影响。文献［17］提出考虑可能性违规风险的分布式光伏承载能力评估方法，但未考虑附加手段对承载力的提升。文献［18］提出基于配电网运行裕度的分布式光伏最佳接入容量评估方法，但未给出分布式光伏准入容量极限。文献［19］提出考虑电压约束的分布式电源最大准入容量双层规划方法，但仅考虑了负荷不确定性。以上方法侧重于评估分布式光伏承载力，未考虑承载力的提升问题。

实际上，从分布式光伏投资规划角度来看，研究分布式光伏承载力的有效提升方法更具有实际意义［20］。一方面，在提升手段上，可采用变压器抽头调节［21］、附加无功补偿［22］、光伏逆变器功率因数调整［23］、网络重构［24］、配置储能［25］、需求侧响应［26］等方法。然而，单一使用某种方式的提升能力有限，需要研究不同提升手段的协同配合以更大限度地提升分布式光伏承载力。此外，不同手段的协调应用中还需要考虑投资运行的经济性。另一方面，源荷不确定性使电网运行指标的概率变化特征更加明显，基于典型日的确定性场景下的承载力评估结果可能易偏保守，不能准确反映真实的分布式光伏承载力水平［27-28］。因此，有必要在承载力评估中综合考虑不确定性因素的影响。

本文从源侧分布式光伏逆变器无功控制、网侧最小附加无功补偿以及网络重构协同优化角度，研究了配电网分布式光伏承载力的提升问题，并综合考虑了源荷双侧不确定性影响，提出一种基于机会约束规划的配电网分布式光伏承载力提升方法。构建了分布式光伏承载力提升的多目标机会约束规划模型，提出采用基于拉丁超立方采样蒙特卡洛模拟（Latin hypercube sampling based Monte Carlo simulation，LHS-MC）嵌入改进初始种群生成策略的协同进化算法对模型进行寻优求解。算例仿真验证了所提方法和求解算法的有效性。

1 配电网分布式光伏承载力及提升

1.1 配电网分布式光伏承载力影响因素

含分布式光伏密集接入的配电网典型结构图如图1 所示。

图1 含分布式光伏密集接入的配电网Fig.1 Distribution network with dense integration of distributed photovoltaic

分布式光伏接入后，改变了配电网线路潮流和电压分布。设配电网馈线上有n个节点，计算线路节点k处的电压Uk为：Uk=U0-

式中：U0为配电网与上级电网连接点处的电压；Ui-1为节点i-1 处电压，i=1，2，…，n；PDG，j和QDG，j分别为节点j上分布式光伏有功和无功功率，j=1，2，…，n；PL，j和QL，j分别为节点j上负荷的有功和无功功率；li为节点i和节点i-1 之间的线路长度；r和x分别为单位长度线路的电阻和电抗。

当节点接入的分布式光伏电源出力大于负荷功率时，该节点出现反向潮流，可以看成是一个向电网注入功率的电源节点。由式（1）可知，分布式光伏出力越大，节点电压越高，且越靠近线路末端，电压抬升越明显。当分布式光伏接入容量达到一定程度时，线路潮流、节点电压可能超出允许值。

需要说明的是，本文不考虑线路和变压器的扩容与改造，配电网可以通过网络结构调整方式改变潮流分布，但调整中必须保证系统满足连通辐射状结构。因此，研究配电网分布式光伏承载力需要综合考虑节点电压安全、支路载流量（即线路载流量和变压器反向负载率）、网络拓扑等约束条件。

1.2 配电网分布式光伏承载力提升措施

分布式光伏部署位置通常由负荷分布和地区资源特性确定，在分布式光伏接入位置给定的前提下，为提升配电网分布式光伏承载力，需要充分挖掘各种可控手段。本文从源侧分布式光伏逆变器无功控制、网侧最小附加无功补偿以及网络重构协同优化角度，研究配电网分布式光伏承载力提升。

1.2.1 分布式光伏逆变器无功控制

源侧分布式光伏通过逆变器并网，其等效并网示意图如图1 中红色虚线框所示。并网分布式光伏在向电网提供有功功率的同时，也可以输出无功功率［29］，可利用并网逆变器自身容量向电网提供无功调节能力，分布式光伏逆变器功率调节范围受其容量限制。

分布式光伏逆变器参与无功调节时，能够提供的最大无功功率Qmax与光伏逆变器容量Smax和当前有功出力PDG有关，如式（2）所示。

分布式光伏逆变器在其无功调节范围内，按照无功电压优化控制需求输出无功功率。电压偏低时，调整光伏逆变器运行在超前方式下，为系统提供无功功率；反之，调整其运行在滞后方式下，从系统吸收无功功率。利用分布式光伏逆变器超前或滞后运行方式下的无功调节能力，对节点电压进行控制，以提升配电网分布式光伏承载力。

1.2.2 附加无功补偿

当仅依靠分布式光伏逆变器的无功调节能力不能满足系统电压控制需求时，就需要网侧通过最小附加无功补偿进一步改善电压水平，从而提升配电网分布式光伏承载力。由于附加无功补偿的接入位置和接入容量会影响电压控制效果，本文采用基于网损灵敏度方法确定附加无功补偿的最佳接入位置，其最小补偿容量则通过第2 章分布式光伏承载力提升的机会约束规划模型优化求解获得。

网损灵敏度综合考虑了潮流方程非线性及附加无功补偿对候选补偿节点的影响［30］。基于网损灵敏度矩阵计算系统网损增量ΔPloss，表达式为：

式中：Ploss为系统总有功网损；u为节点输入功率矩阵；Δu为节点功率增量；∂Ploss/∂u为一阶网损灵敏度；∂2Ploss/（∂u∂u）为二阶网损灵敏度，其具体计算过程见附录A 第A1 节。

对每个节点分别增加单位无功补偿量代入Δu，由式（3）计算网损增量，记为网损无功修正灵敏度。对网损无功修正灵敏度排序，优先选择网损无功修正灵敏度大的节点作为候选最佳无功补偿接入点。

1.2.3 网络重构

配电网网络结构复杂，系统中拥有大量联络开关和分段开关，网络重构通过对开关的断开或闭合状态进行操作，调整配电网网络拓扑、优化系统运行状态，使系统中负荷和电源在馈线间合理分配。

网络重构时，需要满足配电网网络连通性及辐射性要求，避免产生孤岛和环网［31］。一方面，网络重构可以改变配电网运行方式的潮流分布，提升电网电压质量；另一方面，网络重构可以有效降低网络运行损耗，提高系统经济性。因此，网络重构可以作为进一步提升分布式光伏承载力的一种有效手段。

1.3 源荷双侧不确定性对承载力的影响

配电网源端分布式光伏出力具有随机性、波动性；荷端居民负荷、商业负荷等不同类型负荷变化频繁，峰谷差较大，具有不确定性。源荷双侧不确定性使配电网线路潮流、节点电压等运行指标出现概率特征。节点电压达到上限约束通常对应的是光伏出力大发、负荷水平最小的运行方式。本文选择光伏午间大发时段光照强度和各时段负荷水平随机变化场景作为配电网分布式光伏承载力的计算条件，综合考虑分布式光伏出力和负荷的不确定性，引入机会约束规划，避免概率很低的不满足约束条件的极端场景造成承载力计算偏差过大的影响。

本文采用概率密度函数描述源荷不确定性因素，源荷不确定性建模见附录A 第A2 节。

2 分布式光伏承载力提升的多目标机会约束规划模型

为避免源荷不确定性对承载力评估结果偏差过大的影响，采用机会约束规划方法建立分布式光伏承载力优化模型。本章构建以接入分布式光伏容量最大和投资运行总成本最小为目标的配电网分布式光伏承载力提升多目标机会约束规划模型。优化模型中，综合考虑了源侧分布式光伏逆变器无功控制和网侧最小附加无功补偿，以及网络重构手段之间协同配合对配电网分布式光伏承载力的提升。

2.1 目标函数

以接入分布式光伏容量最大，以及额外附加无功补偿投资成本和考虑网络重构后系统运行有功网损成本构成的投资运行总成本最小为目标函数，即

式中：f1为接入的分布式光伏总容量；f2为投资运行总成本；fcost为附加无功补偿投资成本；floss为系统运行有功网损成本；SN为所有节点集合；CDG，i为节点i可接入的分布式光伏容量；SC为附加无功补偿集合；ρQ为附加无功补偿单位容量价格；τ为折现率；y为无功补偿投运年限；QC，k为第k个附加无功补偿容量；rC，k为第k个附加无功补偿固定安装投资成本；ρP为单位有功网损价格；SL为支路集合；dl为支路l的开断状态，1 为支路闭合状态，0 为支路断开状态；Zl为支路l的阻抗；Il为流经支路l的电流。

2.2 约束条件

1）分布式光伏出力约束：

式中：PDG，i和QDG，i分别为节点i上接入的分布式光伏当前输出有功和无功功率，i∈SN；PDG，i，max为节点i上分布式光伏的输出有功功率上限；QDG，i，max为节点i上分布式光伏的输出无功功率上限，由式（2）确定。

2）节点电压安全约束。采用机会约束形式描述节点电压安全约束：

式中：Ui为节点i的电压幅值，i∈SN；Ui，max和Ui，min分别为节点i的电压幅值上限和下限；Pr {·}表示事件成立的概率；βV为节点电压约束的置信水平值。

3）线路载流量约束。采用机会约束形式描述线路载流量约束：

式中：Il，max为线路l允许最大载流；βl为线路载流量约束的置信水平值。

4）变压器反向负载率约束。配电网中的变压器设备应满足热稳定要求，变压器的反向负载率不能超过允许的最大值。采用机会约束描述变压器反向负载率约束条件：

式中：PL，i为节点i上的等效负荷出力；ST，max为变压器T的最大传输容量，T∈ST，其中，ST为变压器集合；λmax为变压器反向负载率最大值，取值为80%［3］；βT为变压器反向负载率约束的置信水平值。

5）网络拓扑约束。网络重构需要满足网络拓扑连通性及辐射性要求。对于网络中任意节点i，均存在一条该节点到源节点的连通闭合路径，同时，网络重构要防止断开辐射状支路，不能出现孤岛和环网情况。网络拓扑连通性和辐射性约束如式（12）所示。

式中：li，0为第i个节点到源节点连通路径包含的支路集合，i∈SN；N为网络中节点总数；L为网络中支路总数。

6）潮流平衡约束：

式中：QL，i为节点i上负荷无功功率，i∈SN；QC，i为节点i上附加的无功补偿量；θi，j为节点i和j间电压相角；Gi，j和Bi，j分别为节点i和j间线路的电导和电纳。

3 分布式光伏承载力优化提升求解

上文所构建的分布式光伏承载力提升的多目标机会约束规划模型，在获得最大分布式光伏承载力的同时，兼顾了不同提升手段协同配合的投资运行成本。由于配电网结构复杂，建立的优化模型变量数巨大，其中，待优化变量不仅包括分布式光伏出力、附加无功补偿量等连续变量，还包括大量网络支路开断状态的离散变量，模型求解复杂，普通优化求解算法可能会出现“维数灾”问题。本文提出采用基于LHS-MC 嵌入改进初始种群生成策略的协同进化算法对模型进行寻优求解。分布式光伏承载力提升问题求解的整体流程，如附录B 图B1 所示。

3.1 多目标机会约束规划模型求解方法

由式（4）至式（13）构成的模型是一个高维、非线性的多目标机会约束规划问题。针对机会约束条件求解，本文采用LHS-MC［32］对机会约束进行校验。针对多目标问题，本文改进Pareto 最优求解算法，采用改进初始种群生成策略的协同进化算法获取多目标的Pareto 解集。最后，基于模糊理论从Pareto 前沿选择最优折中解。

3.1.1 LHS-MC 对机会约束条件校验

拉丁超立方采样（Latin hypercube sampling，LHS）［33］是一种多维分层采样法，在保证模拟精度的同时有效减小了采样次数。采用LHS-MC 的随机模拟技术对机会约束条件进行校验。首先，对随机变量光照强度G/负荷功率PL进行采样，得到D个独立随机变量样本［Gd，PL，d］（d=1，2，…，D）。然后，将随机变量样本依次代入潮流模型中进行随机潮流计算，判断节点电压、线路载流量、变压器反向负载率是否满足约束条件，统计D个采样样本中满足约束条件的样本数D′，若D′/D≥β成立，则认为满足机会约束条件。选择满足所有机会约束条件的个体为可行个体。

3.1.2 改进初始种群生成策略的协同进化算法

协同进化算法［34］将复杂的优化问题分解为多个种群相互关联的子优化问题，更加高效地求取全局最优解。假设待优化控制量按照类型可分为X类，根据控制变量类型划分构建子种群Zx，x=1，2，…，X。分别采用独立的遗传算法进行优化，通过种群间协作保证生态系统的整体优化。

假设种群规模为Ssize，为避免重复随机生成初始种群个体、提高初始种群生成效率和个体质量，提出一种改进初始种群生成策略产生可行的初始个体，即

式中：α为收缩系数，初值取0.5，每次收缩过程α值减半，最终总能使成为可行初始个体。

然后，对各子种群Zx内部按照遗传算法流程进行选择，按照交叉概率pc、变异概率pm进行操作。取目标函数的优化方向为适应度函数值的增加方向，种群Zx选择适应度函数值最大的个体作为种群代表。从对方其他种群Z-x中选择适应度值最高的个体，解码后与自身种群内的个体共同构成系统的控制变量。进一步，基于标准遗传算子更新，完成一代的协同进化过程。重复各种群的协同进化操作，直到达到系统设置的最大遗传代数kmax，输出优化Pareto 最优解集。

3.1.3 基于模糊理论的Pareto 最优解选取

为客观获取最终的承载力优化提升方案，利用基于信息熵的模糊方法从Pareto 最优解集中选取最优解。通过满意度函数描述每个Pareto 最优解中对应各个目标函数的满意程度，偏小型和偏大型目标函数对应的满意度函数计算表达式如附录B 式（B1）、式（B2）所示。Pareto 最优解集中，解的标准化满意度计算表达式如式（B3）所示。

计算Pareto 最优解集中各个解的标准化满意度，选择标准化满意度最大值所对应的最优解作为Pareto 最优折中解，从而得到配电网分布式光伏承载力优化提升的最终方案。

3.2 模型优化求解步骤

配电网分布式光伏承载力提升的多目标机会约束规划模型优化求解流程如附录B 图B2 所示。优化求解具体步骤如下：

步骤1：按照待优化控制量类型将优化模型控制变量分为3 个种群，控制变量包括光伏有功无功出力X1=［PDG，1，PDG，2，…，PDG，i，QDG，1，QDG，2，…，QDG，i］，附加无功补偿量X2=［QC，1，QC，2，…，QC，k］，支路开断状态X3=［d1，d2，…，dl］；

步骤2：按照式（14）改进的初始种群生成策略产生初始群体个体；

步骤3：采用LHS 方法对负荷功率/光照强度随机变量进行采样，得到D个独立随机样本；

步骤4：对配电网进行概率潮流计算，检验初始种群中个体的可行性，逐次校验D个独立随机样本的状态变量是否越限，根据大数定律判断个体是否满足机会约束置信度要求，若不满足则根据式（15）进行收缩靠拢，直到转变为可行个体；

步骤5：重复步骤2 至4，直到生成Ssize个满足机会约束的初始种群；

步骤6：对各个子种群内部按照遗传算法流程进行选择、交叉、变异操作，生成新个体；

步骤7：种群间协同，从对方种群中选择适应度值最高的个体，解码后与自身种群内的个体共同构成系统的控制变量，计算个体的适应度；

步骤8：判断是否满足整体协同优化的终止条件，即是否达到最大遗传代数kmax，若是则终止优化过程，得到Pareto 最优解集；否则，转步骤6，重新寻优计算；

步骤9：利用基于信息熵的模糊方法，从得到的Pareto 最优解集中选取最优折中解。

4 算例仿真

4.1 改进IEEE 33 节点系统算例说明

本文以改进的IEEE 33 节点配电系统为例，计算并验证分布式光伏承载力提升方法的有效性。为模拟分布式光伏密集接入的配电网场景，假设在节点2～33 上每间隔一个节点接入分布式光伏，其实际接入容量为待优化变量。改进IEEE 33 节点系统如图2 所示。图中：红色虚线为联络线，初始为断开状态。

图2 改进IEEE 33 节点系统Fig.2 Modified IEEE 33-bus system

系统中的节点电压安全范围设为0.95～1.05 p.u.；配电网采用常用的LGJ-240 线型，长期允许的最大载流量为600 A；主变压器允许功率倒送，允许的最大传输容量为14.2 MV·A。机会约束中的置信水平βV、βl、βT初始取值均为0.95。光伏逆变器的转化效率η为98.8%，标准额定条件下光照强度为1 000 W/m2。单位有功网损价格取1.5 万元/MW；待优化的附加无功补偿装置的单组额定容量设置为0.1 Mvar，无功补偿单位容量价格取2.5 万元/Mvar，无功补偿装置固定安装投资成本取0.3 万元；折现率τ取10%，无功补偿投运年限为20 年。在Intel Core i5-8250U CPU@1.8 GHz，8 GB RAM 处理器的计算机平台上，基于MATLAB 2018a 编程实现对本文优化模型的求解。LHS 样本数D=400，协同优化的每个种群内部采用标准遗传算法，标准遗传算法的参数Ssize为50，pc为0.75，pm为0.006，kmax为80。

根据某地一年中光伏午间大发时段的光照强度历史样本数据，拟合出光照强度Beta 分布的形状参数为a=2.12，b=51.64。改进IEEE 33 节点系统相应节点负荷及支路阻抗基础数据与文献［35］相同。负荷的不确定性以原始IEEE 33 节点系统中负荷值为均值，标准差取均值的5%，按照正态分布拟合负荷的有功功率，按照原始系统中负荷的功率因数确定负荷无功功率。

4.2 改进IEEE 33 节点系统算例结果分析

1）承载力优化提升效果比较

以分布式光伏电源按照单位功率因数运行，分布式光伏逆变器不参与无功调节且不考虑附加无功补偿及网络重构时的承载力为基础场景（场景0），比较分析了下列4 种场景（场景1～4）中分布式光伏承载力的提升效果：

场景1：仅考虑分布式光伏逆变器无功出力优化调节的承载力；

场景2：仅考虑附加无功补偿的承载力，分布式光伏电源按照单位功率因数运行；

场景3：考虑分布式光伏逆变器无功调节及附加无功补偿协同优化的承载力；

场景4：同时考虑分布式光伏逆变器无功调节和附加无功补偿及网络重构协同优化的承载力。

图3 比较了5 种场景下最优折中解中不同节点接入的分布式光伏容量。表1 给出了5 种场景下分布式光伏承载力优化提升结果。

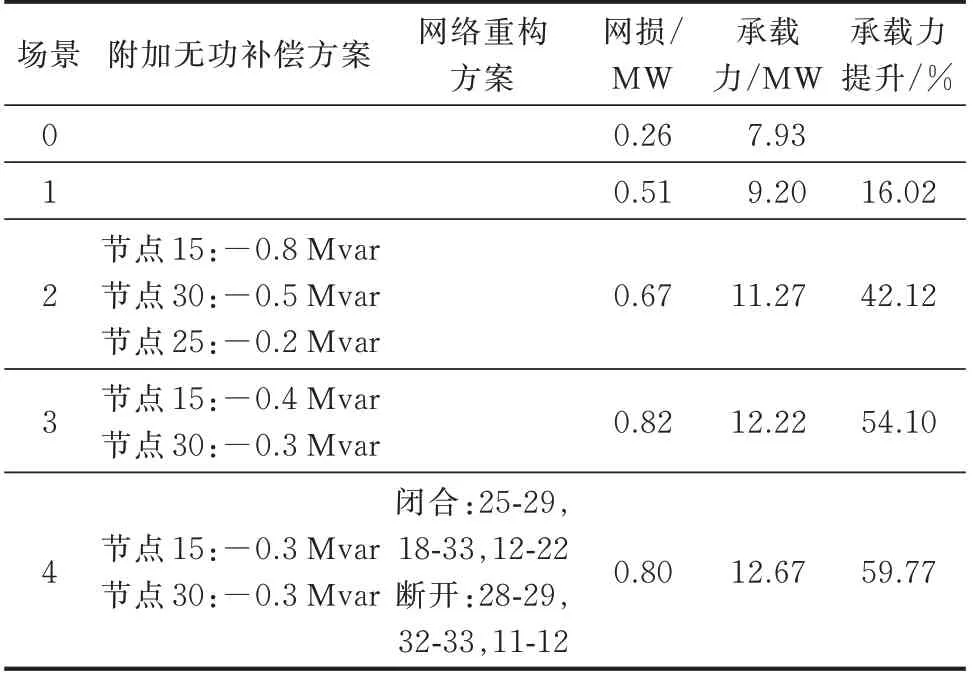
表1 不同场景下的系统分布式光伏承载力Table 1 Distributed photovoltaic hosting capacity in different scenarios

图3 不同节点接入分布式光伏容量优化结果Fig.3 Optimal results of distributed photovoltaic capacity at different nodes

在场景0 中，通过优化计算得到系统对分布式光伏的最大承载力为7.93 MW。

场景1 在仅考虑分布式光伏逆变器无功出力优化调节、不考虑附加无功补偿及网络重构的情况下，计算得到分布式光伏的最大承载力为9.20 MW，相比场景0 的承载力提升了16.02%。

场景2 在仅考虑附加无功补偿、分布式光伏均按单位功率因数运行情况下，需要在3 个节点附加无功补偿（节点15 接入-0.8 Mvar、节点30 接入-0.5 Mvar、节点25 接入-0.2 Mvar 的附加无功补偿），额外附加无功投资贾用为4.65 万元；有功网损为0.67 MW，系统运行有功网损成本为1.005 万元，投资运行总成本为5.655 万元。计算得到分布式光伏的最大承载力为11.27 MW，相比场景0 承载力提升了42.12%。

场景 3 优化求解得到在节点 15 接入-0.4 Mvar、节点30 接入-0.3 Mvar 的附加无功补偿，额外附加无功投资贾用为2.35 万元；有功网损为0.82 MW，系统运行有功网损成本为1.23 万元，投资运行总成本为3.58 万元。综合考虑了分布式光伏逆变器无功调节及附加无功补偿后，计算得到分布式光伏的最大承载力为12.22 MW，相比场景0承载力提升了54.10%。

场景4 优化求解得到在节点15 接入-0.3 Mvar、节点30 接入-0.3 Mvar 的附加无功补偿，网络重构需要闭合联络线开关25-29、18-33、12-22，同时断开支路开关28-29、32-33、11-12，网络重构后系统拓扑结构如附录C 图C1 所示。 系统有功网损为0.80 MW，投资运行总成本为3.3 万元。优化得到的承载力为12.67 MW，相比场景0 承载力提升了59.77%。可见，场景4 同时考虑分布式光伏逆变器无功调节和附加无功补偿，以及网络重构协同优化对分布式光伏承载力的提升效果最为明显，同时有效降低了投资运行总成本。

2）不同置信水平对承载力的影响分析

改变机会约束规划模型中节点电压、线路载流量、变压器反向负载率约束的置信水平取值，βV、βl、βT分别在［0.80，1.00］范围内取值。假设当其中一个约束条件置信水平在［0.80，1.00］变化时，保持其他两个约束条件置信水平固定为初始取值0.95，计算节点电压、线路载流量、变压器反向负载率约束在不同置信水平下配电网的分布式光伏承载力，结果如附录C 图C2 所示。表2 比较了不同置信水平下计算得到的配电网分布式光伏承载力。

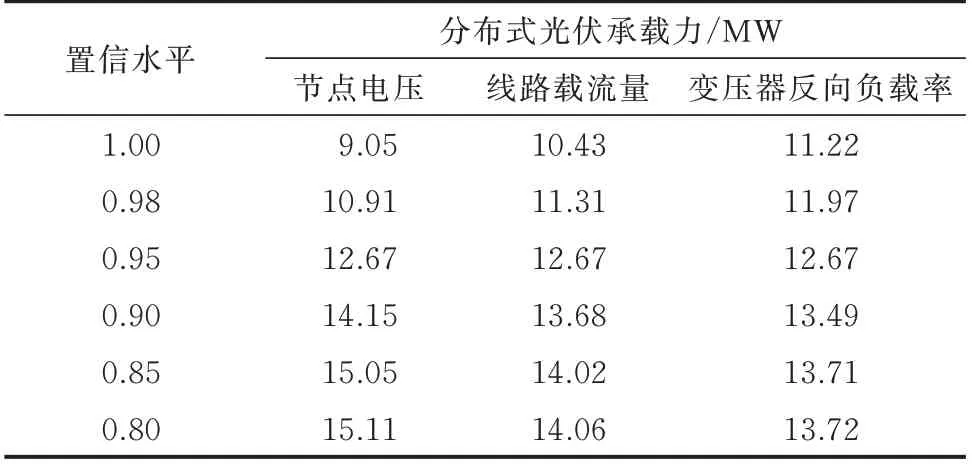
表2 不同置信水平下的分布式光伏承载力Table 2 Distributed photovoltaic hosting capacity at different confidence levels

置信水平值取值为1.00 时，对应为不考虑源荷不确定性对该参数变量的影响。当节点电压的置信水平由1.00 变化为0.80 时，对应的分布式光伏承载力由9.05 MW 变化为15.11 MW，相比场景0 计算得到的承载力（7.93 MW），提升水平由14.12%提高到90.54%；线路载流量的置信水平由1.00 变化为0.80 时，对应的分布式光伏承载力提升水平由31.53%（10.43 MW）变化为77.30%（14.06 MW）；变压器反向负载率约束置信水平由1.00 变化为0.80时，对应的分布式光伏承载力提升水平由41.49%（11.22 MW）变化为73.01%（13.72 MW）。

可见，随着参数置信水平值的减小，配电网分布式光伏承载力逐渐增大，参数置信水平值降低到一定程度后的分布式光伏承载力会明显受到其他参数约束条件的限制而趋于稳定。在节点电压、线路载流量、变压器反向负载率3 个机会约束中，节点电压参数的置信水平变化对分布式光伏承载力提升效果的影响最为显著。在实际规划中，根据电网实际情况对机会约束条件确定置信水平值。

3）算法比较分析

分别采用LHS-MC 和基于简单随机采样的蒙特卡洛模拟（simple random sampling based Monte Carlo simulation，SRS-MC）法对机会约束条件进行校验。简单随机采样（simple random sampling，SRS）次数为5 000 次，LHS 次数为400 次。图4 所示为采用不同方法进行概率潮流计算后，馈线末端节点18 的电压概率密度曲线。

图4 LHS-MC 和SRS-MC 法对约束条件校验结果比较Fig.4 Result comparison of constraint condition verification between LHS-MC and SRS-MC methods

LHS-MC 和SRS-MC 法对机会约束校验准确度基本一致，但采用LHS-MC 法校验机会约束条件需耗时0.529 s，而采用SRS-MC 法则需耗时6.682 s。LHS-MC 法在机会约束条件校验过程中，保留了SRS-MC 法的高精度，同时校验计算耗时仅为SRS-MC 法的7.92%，提高了校验效率。

图5 对比了采用协同进化算法与常规遗传算法和模拟退火遗传算法求得的Pareto 最优前沿。表3比较了3 种算法得到的最优折中解结果。

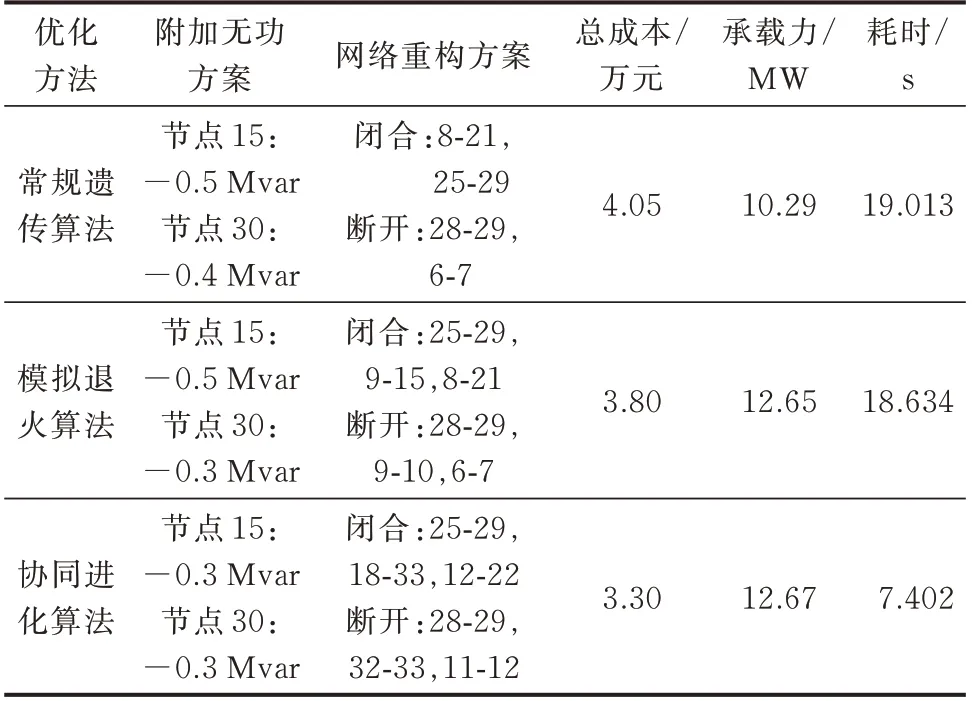
表3 不同优化方法的计算结果Table 3 Results of different optimization methods

图5 Pareto 最优前沿结果Fig.5 Pareto optimal frontier results

由表3 可以看出，在求解速度方面，协同进化算法采用多种群协同优化流程，耗时7.402 s 得到最优解，而常规遗传算法计算需耗时19.013 s，模拟退火遗传算法需耗时18.634 s 才能得到最优解。协同进化算法优化求解效率相比常规遗传算法提升了61.07%，相比模拟退火遗传算法提升了60.28%。在求解质量方面，常规遗传算法从Pareto 最优解集中选取的最优解为：节点15 接入-0.5 Mvar、节点30 接入-0.4 Mvar 的无功补偿；同时，重构后系统分布式光伏最大承载力为10.29 MW；模拟退火遗传算法得到的最优解为：节点15 接入-0.5 Mvar、节点30 接入-0.3 Mvar 的无功补偿，重构后系统分布式光伏最大承载力为12.65 MW；协同进化算法得到的最优解为：节点15 接入-0.3 Mvar、节点30 接入-0.3 Mvar 的无功补偿，重构后系统分布式光伏最大承载力为12.67 MW。可见，常规遗传算法得到的解偏保守；模拟退火遗传算法得到的最优承载力结果与协同进化算法相当，但投资运行总成本偏大；协同进化算法得到的最优解质量最高。综上，在求解效率以及求解质量方面，协同进化算法相比于常规遗传算法和模拟退火遗传算法呈现出更好的优势。

5 结语

针对未来分布式光伏密集接入配电网规划运行需求，本文提出一种基于机会约束规划的配电网分布式光伏承载力提升方法，并得到以下几点结论：

1）所提出的方法考虑了源荷双侧不确定性对配电网分布式光伏承载力的影响。算例分析表明，节点电压的置信水平变化对分布式光伏承载力提升效果的影响最为显著，随着参数置信水平值的减小，承载力逐渐增大，参数置信水平值降低到一定程度后的承载力会明显受到其他参数约束条件的限制而趋于稳定。

2）所建立的配电网分布式光伏承载力提升多目标机会约束规划模型，从分布式光伏容量规划与运行一体化角度综合考虑了系统安全运行约束，既能优化计算提升后的配电网分布式光伏承载力，又能兼顾投资运行总成本最小的经济性要求。

3）所提出的基于LHS-MC 嵌入改进初始种群生成策略的协同进化算法保留了传统蒙特卡洛模拟法的高精度，同时提高了机会约束校验效率，在优化模型求解方面，相比于常规遗传算法和模拟退火遗传算法具有更优的求解搜索能力和求解效率。

4）综合本文研究表明，通过源侧分布式光伏逆变器无功控制和网侧最小附加无功补偿以及网络重构协同优化，可有效提升配电网分布式光伏承载力，并减少附加无功投资及运行总成本需求。优化提升后的承载力结果可为配电网分布式光伏规划建设提供参考。

配电网分布式光伏承载力受多方面因素影响，如配电网中分布式电源及负荷资源配置、网架结构、运行安全约束、经济性要求等。本文的研究是在不考虑线路和变压器扩容与改造条件下开展的，下一步可考虑配电网设备扩容对配电网分布式光伏承载力的影响及提升问题研究。此外，配电网中的分布式储能、电动汽车等灵活资源接入后，也将对配电网分布式光伏承载力产生影响，上述问题有待今后系统、深入地进行研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。