提炼基本图形，注重思想方法

杨帅

【摘要】数学思想方法是数学的灵魂，数学教学应通过数学知识的教学和适当的解题活动重点突出数学思想和方法。以“解直角三角形中有关测高测距专题”为例，将教材中部分教学内容进行重组变式，设计解直角三角形中有关测高测距的专题课，从而让学生体会数学思想方法对解决问题的重要意义。

【关键词】提炼基本图形；数学思想方法

根据著名数学家波利亚的调查研究，数学思想方法比形式化的数学知识更具有普遍性，在学生未来的生活和工作中应用更加广泛。“即使学生把所学的知识（概念、定理、法则和公式等）全忘了，铭刻在他心中的数学精神、思想和方法却能使他终身受益。” 所以，数学教学应通过数学知识的教学和适当的解题活动重点突出数学思想和方法。为此，本文以“解直角三角形中有关测高测距专题”为例，进行了如下的教学设计。

一、教学内容解析

对于锐角三角比的教学内容，主要从定量方面研究直角三角形。直角三角形中边角之间的数量关系，可以通过三角形内角和定理、勾股定理和锐角三角比进行表述。基于这些数学工具，就能解决实际生活中的许多问题，如测量物体的高、测量两点间的距离等。本文的教学设计针对沪教版数学教材九年级第一学期第25章第4小节“解直角三角形的应用”进行例题讲解。笔者认为，将这部分教学内容进行重新编排，将有关测量物体高度和测量两点间距离这个专题问题在前两个课时完成，其中，第1课时的教学内容可与教材的编写内容一致，即完成俯角和仰角概念的介绍。对于第2课时，本文给出详细的教学设计，具体以例3、例4和例5（教材中的例9）为依托，领会化归思想、方程思想在几何计算中的运用，从而让学生体会数学思想方法对解决问题的重要意义。

二、教学目标及重难点设置

1．教学目标

（1）运用解直角三角形的相关知识，解决测量两点间距离和物体高度（底部不能达到）的简单实际问题。

（2）在解决实际问题时，进一步领会化归思想、方程思想、从特殊到一般以及从一般到特殊的思想方法。

2．教学重点及难点

重点：领会化归思想，运用解直角三角形的方法解决有关实际问题。难点：提炼基本图形，利用方程思想解决有关实际问题。

三、学生学情分析

学生掌握锐角三角比的基本概念之后，可以利用锐角三角比以及勾股定理，对直角三角形进行定量分析。在初中，解直角三角形是解决任意三角形中计算问题的基础，求解任意三角形中的元素都可以通过先构造合适的直角三角形，然后再解直角三角形。这些已掌握的知识为实际应用背景下解直角三角形的问题奠定了基础，但是当图形中有一条公共直角边的两个直角三角形时，每个直角三角形的已知条件都不完备，不可直接求解，那么此时该如何解决问题呢？这是本节课要解决的问题。

四、教学过程

1.复习回顾

教师出示PPT，呈现上节课测量旗杆（例题1）和楼房高度（例题2）的问题，一步一步引导学生回忆解决步骤，思考解决方法，为接下来的进一步学习作铺垫。

2.例题讲解

今天我们继续研究其他距离和高度的问题。

例3：如图1，在港口A的南偏东52°方向有一座小岛B，一艘船以每小时24千米的速度从港口A出发，沿正东方向行驶。

问题（1），若20分钟后，这艘船在C处且测得小岛B在船的正南方向，小岛B与港口A相距多少千米（精确到0.1千米）？

设计意图：

（1）把教材中的例3以问题（1）的形式进行阐述是为了引出问题（2），问题（2）作为本节课的课后思考题（见下文“5.课后思考”），检测学生是否掌握本节课的重点，能否在解决实际问题时进行拓展和变通。

（2）这个实际问题的解决过程涉及到两个转化：一是将实际问题转化为数学模型；二是将数学模型转化为解直角三角形的问题。通过这两个转化，可运用解直角三角形的相关知识，解决例3问题（1）中的几何计算问题，为例4的难度提升作准备。

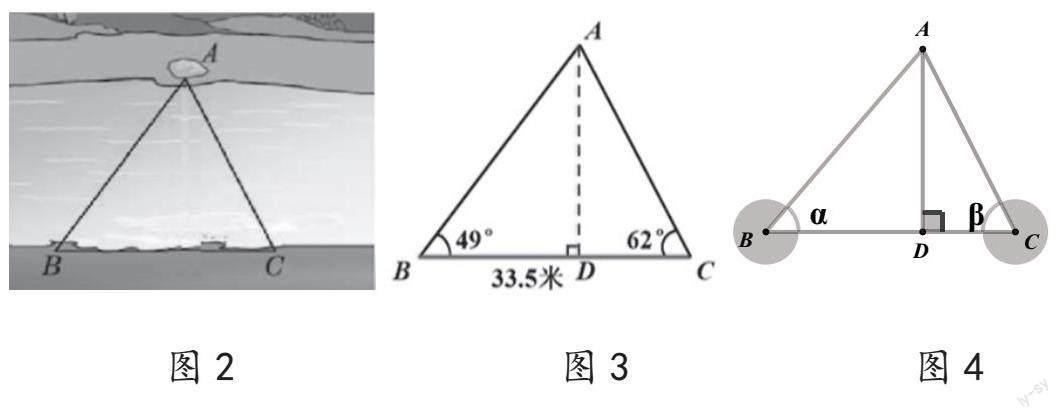
例4：如图2，为了测量河宽，在河的一边沿岸选取B、C两点，对岸岸边有一块石头A，在△ABC中，测得∠B=49°，∠C=62°，BC=33.5米，求河宽（精确到0.1米）。

变式1：当条件改为∠B=α，∠C=β，BC=m米，你能用含α，β，m的表达式表示河宽吗？

设计意图：

（1）从图2到图3，将实际问题转化为数学问题。求解这个三角形的高，需通过添加辅助线构造直角三角形；但图中的两个直角三角形的已知条件都不完备，不可直接求解，如何解决呢？可将公共的直角边AD设为x，利用BC的长度作为等量关系式，采用方程思想求解。

（2）从例4到“变式1”让学生体会在数学中研究问题时从特殊到一般的思想方法。

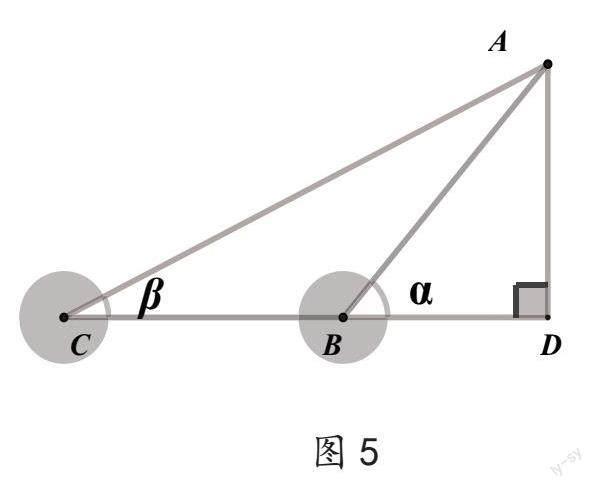
变式2：当人位于点B处，只能朝左边走m米到达点C处，如图5所示，你能用含α，β，m的表达式表示河宽吗？

设计意图：

（1）为了帮助学生理解此问题，笔者借助于“几何画板”，录制了一个7秒钟的小视频（如图6）。该视频展示了当点B从线段CD的延长线上运动到线段CD上时，整个图形的运动变化过程，再比较图4和图5的异同。图4中有一个锐角三角形和两个直角三角形，图5中有一个钝角三角形和两个直角三角形，相同点是两个直角三角形都有一条公共的直角边，引导学生提炼出这个基本图形“有一条公共直角边的两个直角三角形”。

（2）“变式2”相对于“变式1”而言，图形有所不同，但解决问题的方法是相同的，依然是利用方程思想。此外，可为解答初三数学综合题所涉及的相应问题作准备，即由于點的位置不同，从而引起图形发生变化，但解决问题的方法是类似的。

例5（教材中例9）：如图7，小明想测量塔CD的高度。塔在围墙内，小明只能在围墙外测量，这时无法测得观察点到塔的底部的距离，于是小明在A处仰望塔顶，测得仰角为29°25′，再往塔的方向前进50米至B处，测得塔顶的仰角为61°42′，（点A、B、C在一直线上），若小明的身高忽略不计，你能求出塔的高度吗？（结果精确到0.1米）

设计意图：

（1）从“变式2”到例5再次体会在数学中研究问题时从一般到特殊的思想方法，只要把相关数据代入到“变式2”的一般性结论即可解答此题（图7即为图5的特殊情况）。

（2）从知识体系的完整性看，把教材中后面的例9作为本节课中例5更为合适，这个基本图形“有一条公共直角边的两个直角三角形”也可用于解决底部不能到达的物体测高问题。

3．问题探究

同学们，如果你们站在黄浦江边的外滩观景大道处，利用皮尺、计算器和测角仪：

（1）通过平面示意图，你们能通过测量估算出黄浦江宽度吗？

（2）通过三维立体图，你们能通过测量估算出东方明珠的高度吗？

（3）通过三维立体图，你们能通过测量估算出东方明珠下面两个球之间的距离吗？

设计意图：在完成了测高测距专题的教学之后，学生能否解决身边的测高、测距这些实际问题呢？比如估测黄浦江的宽度可以利用“图4”，估测东方明珠的高度可以利用“图5”……让学生畅所欲言，体会数学学科的实用性。

4.归纳小结

通过这节课的学习，同学们有哪些收获？整堂课用到了哪些数学思想方法？

5.课后思考

例3：如图8，在港口A的南偏东52°方向有一座小岛B，一艘船以每小时24千米的速度从港口A出发，沿正东方向行驶。

问题（2），若10分钟后，这艘船到达小岛B的北偏西25°的D处时，收到消息：“小岛B处四周6海里范围内有暗礁！”请你判断一下，若这艘船继续向正东方向行驶，是否有触礁的危险。

设计意图：

应用本节课的知识，思考例3中的问题（2），对解直角三角形中有关测高测距的专题问题进行巩固和提高。

五、评析

数学是一门系统性很强的学科。在教学过程中，既可以参照教材的内容，将一章的若干节直接作为一个单元进行讲授，也可以适当重组部分内容，构成一个单元中的专题。在本文中，笔者将教材中部分教学内容进行重组，设计解直角三角形中有关测高测距的专题课。在“测河宽”的问题情境上深入研究问题，加以变式，提炼并分析图4和图5这两个基本图形，找出图形的共同特点“有一条公共直角边的两个直角三角形”。

从思维的角度看，现代信息技术是人类头脑的延伸，除了计算、作图、统计、推理及证明，还可以模拟实验，拓展想象，促进理解。本节课笔者借助“几何画板”，展示了当点B的位置发生变化时，图4和图5两幅图的动态生成情况，帮助学生从静态和动态、局部和整体、理论和应用的各个方面去研究和探索数学问题。因此，数学课堂应尽可能使用现代教育技术，因为现代教育技术具有的卓越性能，更有利于学生成为真正的学习主体。

数学思想方法也是数学知识的本质，它为分析、处理和解决数学问题提供了指导方针和解题策略。本节课讲授的测高测距专题体现了类比、化归等思想方法，从本质上讲，解直角三角形的实际应用问题均可以转化为解直角三角形或一般三角形的问题。在任意三角形中，知道两边及夹角，两角及夹边，两角及对边，三边，都可通过构造合适的直角三角形，将解一般三角形问题转化为解直角三角形问题，为高中数学解任意三角形做准备。

六、结束语

数学教育的功能应该包括启发学生好奇心，激发他们的求知欲。为达到这样的目标，数学教师必须对教材加以分析和研究，以具体的数学知识为载体，不仅要帮助学生总结归纳基本图形和解题技巧，更要把其中蕴含的数学思想方法化有形于无形，这样才能使学生拥有数学的眼睛和翅膀，看得更远，飞得更高。

【參考文献】

[1]涂荣豹，王光明，宁连华．新编数学教学论[M]．上海：华东师范大学出版社，2006.

[2]刘小蕾．基于单元视角的知识脉络进行课时设计优化的基本方法[J]．上海中学数学，2021（12）.