基于机器学习与气象灾害指标的苹果相对气象产量预测

2023-09-23茹晓雅何建强

农业机械学报 2023年9期

罗琦茹晓雅姜元冯浩于强何建强

(1.西北农林科技大学旱区农业水土工程教育部重点实验室,陕西杨凌 712100;2.西北农林科技大学中国旱区节水农业研究院,陕西杨凌 712100;3.中国科学院水利部水土保持研究所黄土高原土壤侵蚀与旱地农业国家重点实验室,陕西杨凌 712100;4.陕西省气象局秦岭和黄土高原生态环境气象重点实验室,西安 710016)

0 引言

目前,我国黄土高原是全世界最大的苹果(MaluspumilaMill.)种植区之一,其苹果种植面积和产量分别占全球的25.2%和26.3%[1-2]。由于苹果种植业的经济效益较高,黄土高原大部分传统农田都已改建为苹果园,苹果产业已成为当地农村经济的支柱产业之一,是当地农民的主要收入来源。因此,及时准确地预测苹果产量对当地苹果产业的发展具有重要意义。

黄土高原大部分地区光热资源丰富、昼夜温差大,对苹果树的生长发育和结果极为有利[3]。降水、气温和太阳辐射是影响苹果生长发育的重要气象要素,但气象灾害也会对苹果产量形成过程造成极大的影响。黄土高原地区干旱少雨,属于典型生态脆弱区,容易发生各种气象灾害。已有相关研究分析了各类气象灾害对苹果产量的影响。例如,RODRIGO[4]发现春季花期冻害很少导致果树死亡,但会严重损害苹果花芽,是限制苹果产量的关键因素;韩文静等[5]采用连阴雨指标分析发现苹果着色成熟期和采收期受到连阴雨危害的程度高于其他生育期;戴安然等[6]研究结果表明,旱灾是限制中国苹果生产发展的主要因素之一,会使果树正常生长受到抑制,导致叶片萎蔫、落果、枝条抽干等。此外,干旱指标中标准化降水蒸散发指数(Standardized precipitation evapotranspiration index,SPEI)对降水和潜在蒸散发同样敏感,1—6个月尺度的SPEI可用于评估农业干旱,且该指标还被广泛应用于不同作物的产量预测模型中[7]。

为了量化气象因子和气象灾害因子对苹果产量的影响,有必要建立上述因子和苹果产量之间的数学映射关系。但是不同气象因子和气象灾害因子之间存在较强的共线性,并且这些因子与苹果产量之间通常为非线性关系,将传统的线性模型应用于作物产量预测往往不能获得理想的预测结果。近年来,机器学习算法由于其众多优势而逐渐被广泛应用于作物产量预测研究[8]。这类方法从训练数据集中提取信息建立统计模型,随后根据测试数据集评估模型模拟精度,从而在自变量和非自变量之间建立非线性关系[9-10]。相关研究表明机器学习算法可在苹果产量预测中取得较好的效果。例如,LI等[11]利用气象数据和支持向量机(Support vector machine,SVM)算法对陕西省28个基地县的苹果进行了估产,但研究区域只限制于陕西省;KHAN等[12]基于农业生产总值建立了基于列文伯格马夸尔特(Levenberg-Marquardt optimization,LM)、尺度共轭梯度(Scale conjugate gradient back propagation,SCG)、贝叶斯正则化反向传播神经网络(Bayesian regularization back propagation,BRBP)算法的苹果产量预报模型,但其选择的模型输入变量并不包括影响苹果产量形成的环境因素;景辉等[13]采用气象数据和多元线性回归(Multiple linear regression,MLR)、反向传播神经网络(Back propagation neural network,BPNN)算法建立了苹果产量早期预测模型,但并未考虑气象灾害因子对苹果产量的影响,且只考虑了各生育期内气象因子对苹果产量的影响。总体而言,上述研究的不足在于研究区域往往较小,所选择的苹果产量预测模型输入特征变量较少考虑苹果生长季内不同月份气象因子的影响,以及气象灾害因子对苹果产量的影响。

本文以我国黄土高原苹果产区为研究区域,基于气象、空间和气象灾害3类特征变量与产区苹果单产统计数据,选择梯度提升树(Gradient boosting decision tree,GBDT)、SVM和BRBP神经网络3种机器学习算法和MLR算法,构建黄土高原苹果相对气象产量预测模型。首先,采用斯皮尔曼相关性分析确定影响黄土高原苹果相对气象产量的最重要气象特征变量,然后以最重要气象特征变量、气象灾害特征变量和空间特征变量为输入变量,选择苹果相对气象产量预测模型的最佳模型输入特征变量组合,最后基于不同生育期和生长季内各月份的最佳模型输入特征变量组合,分析不同模型预测苹果产量的提前期,以期为黄土高原苹果产量早期预测提供科学依据和技术参考。

1 材料与方法

1.1 研究区域

研究区域为我国黄土高原苹果产区,主要包括河南、山西、陕西和甘肃4省在内的共86个苹果基地县(34°22′～37°42′N,104°53′～112°46′E,海拔84～4 216 m,图1)。黄土高原属于半干旱大陆性季风气候,是我国最大的苹果优生区,其多项气象因素能满足优质苹果生长需求。研究区内年均温为6～16℃,年降水量为201～1 010 mm,年日照时数为1 294～2 900 h。

图1 黄土高原86个苹果生产基地县和气象站点分布图

1.2 数据来源与处理

1981—2017年共37年的逐日气象观测数据(包括降水量、平均气温、最高气温、最低气温、日照时数及空气相对湿度等)来源于中国气象科学数据共享网(CMDSSS,http:∥cdc.cma.gov.cn/)。气象观测站空间位置信息(包括经度、纬度、海拔)来自各县市内的气象观测站。河南、山西、陕西和甘肃共86个县级行政区的苹果单产数据来自《河南统计年鉴》[14]、《山西统计年鉴》[15]、《陕西统计年鉴》[16]和《甘肃发展年鉴》[17],以及各市人民政府依申请公开数据(表1)。本文剔除了各县市单产缺失年份,共获得1 852个有效单产数据。

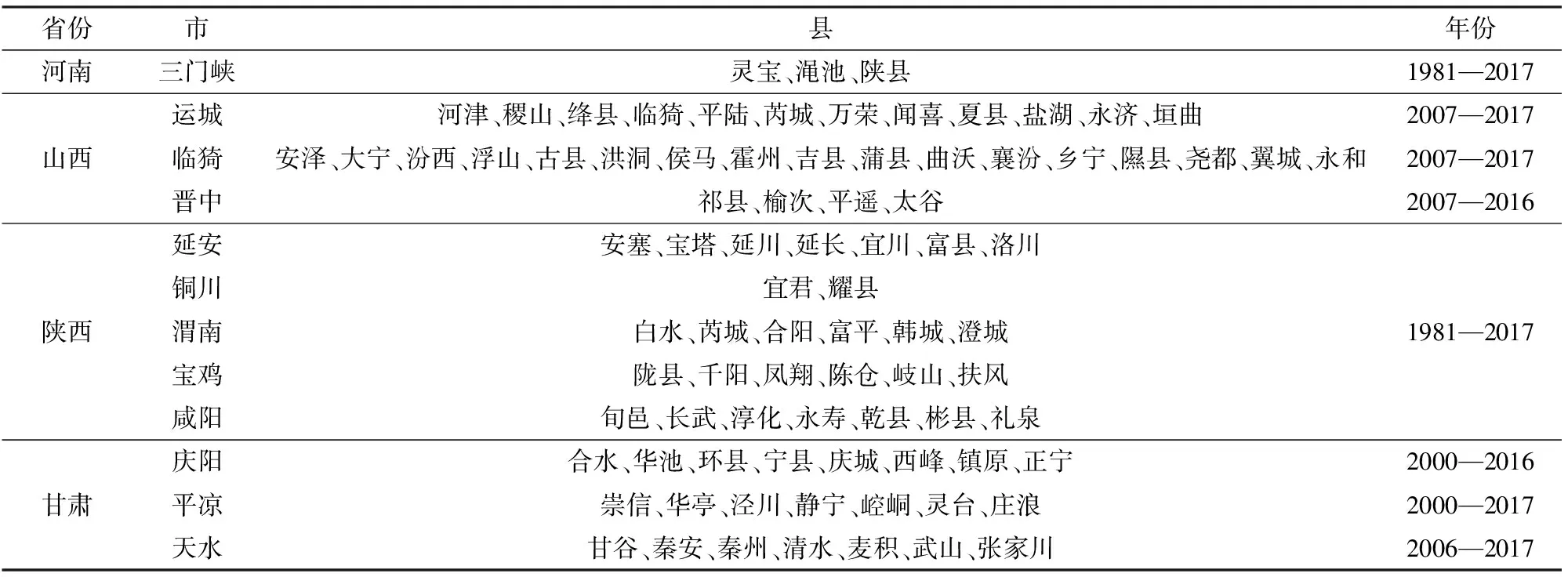
表1 黄土高原苹果产区86个生产基地县产量记录年份

数据归一化处理可消除不同数据的量纲影响,提升模型各项性能[18]。因此,模型建立前统一对输入数据进行归一化处理,最后将模型输出值进行反归一化处理。计算公式为

(1)

式中xn——归一化后的输出数据

x——待归一化的输入数据

xmax——待归一化输入数据最大值

xmin——待归一化输入数据最小值

1.3 模型输入特征变量和目标变量

1.3.1模型输入特征变量优选

依据文献[19-20],黄土高原产区的苹果全生育期为本年11月至次年10月,可主要划分为落叶期(本年11月)、休眠期(本年12月—次年2月)、萌芽幼果期(次年3—5月)、果实膨大期(次年6—8月)和着色成熟期(次年9—10月)。本文选取不同苹果生育期内的9个气象特征变量、3个空间特征变量和3个气象灾害特征变量作为构建苹果相对气象产量预测模型的输入变量,具体特征变量如表2所示。

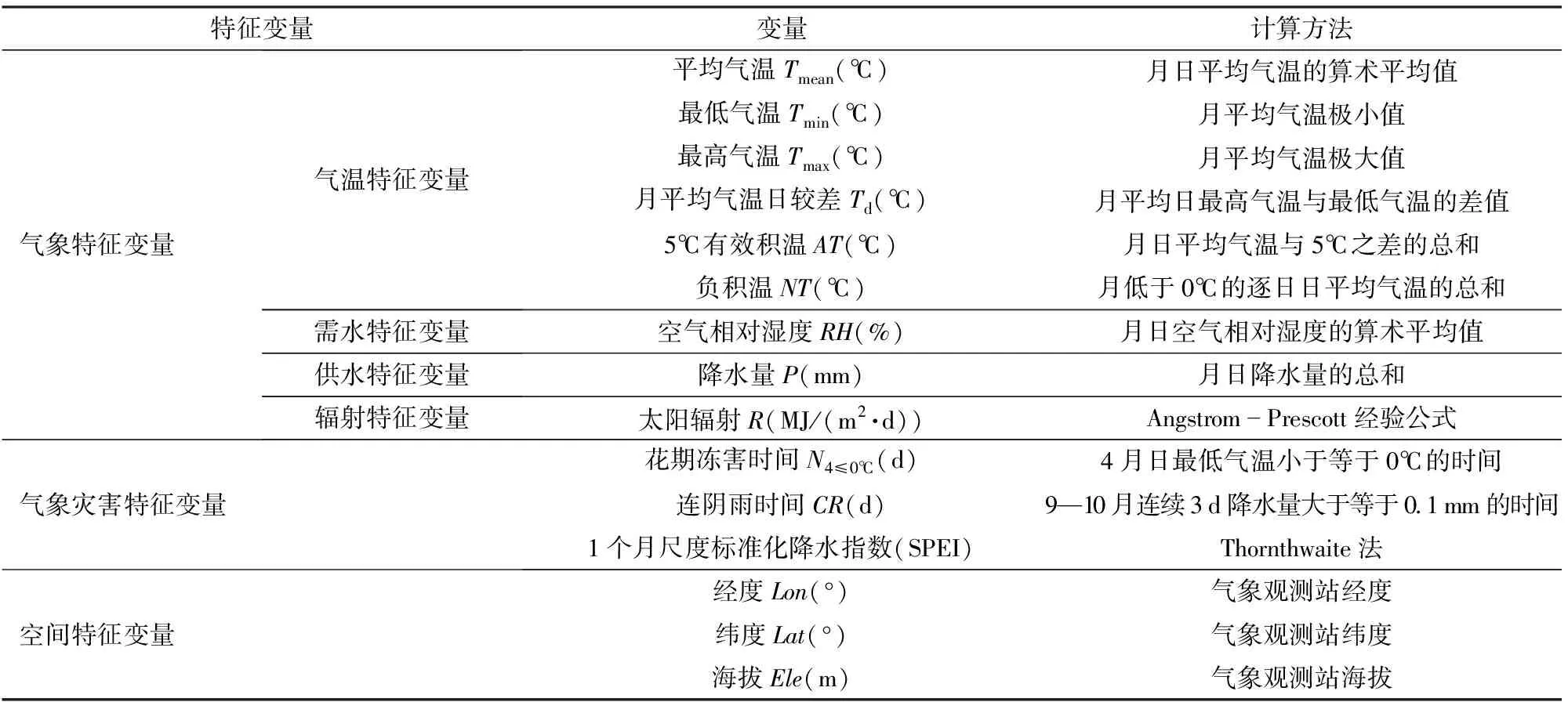
表2 苹果相对气象产量模拟模型输入特征变量

太阳辐射数据根据各气象站点观测的日照时数和Angstrom-Prescott经验公式[21]进行估算,公式为

(2)

其中

Ra=(24×60/π)Gscdr(ωssinφsinδ+

cosφcosδ)

(3)

dr=1+0.033cos(2πJ/365)

(4)

δ=0.409sin(2πJ/365-1.39)

(5)

ωs=arccos(-tanφtanδ)

(6)

N=24ωs/π

(7)

式中N——最大可能日照时数,h

ωs——太阳时角,rad

φ——纬度,rad

δ——太阳磁偏角,rad

J——年内某天的日序数

dr——日地间相对距离的倒数

Gsc——太阳常数,取0.082 MJ/(m2·min)

Ra——大气外总辐射,MJ/(m2·min)

as、bs——经验系数,取0.19和0.54[22]

n——实际日照时数,h

Rs——地表总辐射,MJ/(m2·min)

1个月尺度标准化降水指数(SPEI)根据Thornthwaite法[23]通过R语言中的“SPEI”包计算得到,具体计算过程主要分为3个步骤。

(1)计算潜在蒸散量PET,计算式为

(8)

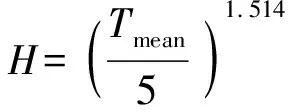
(9)

A=6.75×10-7H3-7.71×10-5H2+

1.792×10-2H+0.49

(10)

式中A——常数

H——年热量指数

PETi——月潜在蒸散量,mm/d

(2)计算气候水平衡,计算式为

Di=Pi-PETi

(11)

式中Di——月降水量与蒸散量差值,mm/d

Pi——月降水量,mm/d

(3)对Di数据序列标准化,采用三参数的log-logistic概率分布F(x)对其进行拟合,计算出每个Di对应的SPEI值,计算式为

(12)

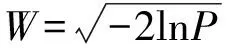
(13)

(14)

式中SPEI——1个月尺度标准化降水指数

其中C0、C1、C2、d1、d2、d3为常数项,取2.515 517、0.802 853、0.010 328、1.432 788、0.189 269、0.001 308。

为消除气象变量多年周期性循环的影响,本文将苹果多年生长季内的气象特征变量进行平均,再将其与目标变量(苹果相对气象产量)进行斯皮尔曼相关性分析(Spearman correlation analysis),选择对苹果产量影响最大的重要气象特征变量,以减少输入数据的复杂程度。在每类气象特征变量中,选择与目标变量的相关系数绝对值最大且显著的特征变量。如果同类特征变量之间的相关系数小于0.5且其与目标变量显著相关时,则可选择多个特征变量。

1.3.2模型目标变量构建

苹果产量的形成受多种因素的影响,主要包括气象要素、技术措施和其他因素,相应地苹果产量可以分解为气象产量、趋势产量和随机产量。为了能更好地反映气象要素造成的苹果产量波动,降低时间和地域对产量影响的限制,采用相对气象产量作为目标变量定量评估气象要素对产量形成的影响。计算公式为

(15)

其中

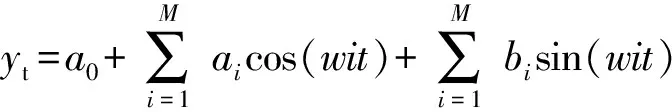
(16)

yc=y-yt+yr

(17)

式中y——实际产量,kg/hm2

yw——相对气象产量,正值表示气象要素有利于作物生长发育即产量增加,负值表示产量减少

yt——趋势产量,kg/hm2,可采用一阶傅里叶拟合来估算[24]

yc——气象产量,kg/hm2

yr——随机产量,kg/hm2,本文忽略不计

a0——常系数,取-2.94×1010～2.17×1011

w——常系数,取0.30～0.90

ai——各级系数,取-2.17×1011～2.94×1010

bi——各级系数,取-2.09×104～1.22

M——傅里叶展开级数,取1

t——年份

1.4 苹果相对气象产量模拟模型

1.4.1机器学习算法

(1)梯度提升树

梯度提升树(GBDT)是基于Booting方法的集成模型。该类方法采用加法模型和前向分步算法实现学习优化[25]。GBDT回归算法中以回归树作为弱学习器,学习任务时,利用损失函数的负梯度作为当前学习器的伪残差,根据伪残差拟合回归树,直到满足要求停止重复此过程。GBDT算法一般比随机森林算法的训练结果更准确[9],收敛速度快且不易出现过拟合。R语言中提供了GBDT算法包“gbm”,所需要的参数包括:分布函数(distribution,选择“gaussian”)、树终节点的最小个数(n.minobsinnode,取10)、学习率(shrinkage,取0.01)、回归树数量(n.trees,取200)以及单棵回归树最大深度(interaction.depth,以1为步长在[0,10]内取值)。

(2)支持向量机

支持向量机(SVM)通过非线性映射将自变量映射到高维的特征空间,在高维特征空间中寻找一个最优超平面,使得所有训练样本距离该最优分类面误差最小[26]。对于回归应用,SVM算法主要利用核函数构造线性回归方程求得最优超平面[27]。该算法可利用R语言提供的“e1071”包来实现,所需参数包括:核函数类型(Kernel,定为高斯径向基核函数)、核函数系数(gamma,以0.01为步长在[0.01,1.00]内选择)以及惩罚系数(cost,以0.1为步长在[0.1,100]内确定)。

(3)贝叶斯正则化反向传播神经网络

贝叶斯正则化反向传播神经网络(BRBP)融合传统反向传播神经网络算法和贝叶斯理论自动选择最优的正则化参数,能够避免过拟合问题,极大提高模型的泛化能力[28]。采用包含输入层、隐含层和输出层的3层神经网络拓扑结构,隐含层的节点数根据试凑法,以预测误差最小为原则来确定。Matlab软件中的“newff”函数可以实现该类算法,所需参数包括:输入节点数a、输出节点数b、隐含层节点数l、节点传递函数(隐含层为tanh,输出层为purelin)、训练函数(trainbr)、迭代次数k、学习率η以及目标函数误差(goal)。其中,参数k、η、goal经反复试算后分别取1 000、0.1、10-5。

(4)多元线性回归

多元线性回归(MLR)是一种广泛应用于单个目标变量与2个及以上输入特征变量的线性回归方法[29]。目标变量通常受多种特征变量的影响,因此多元线性回归相对于一元线性回归更具适用性。在多元线性回归中,方程的参数通过最小二乘法获得[30]。R语言提供的“lm”函数可实现MLR算法。

1.4.2苹果相对气象产量模拟模型构建

如图2(图中M、G、D分别表示最重要气象灾害特征变量、空间特征变量、气象灾害特征变量)所示,以GBDT算法为例,简述苹果相对气象产量yw预测模型的建立过程。首先,基于苹果全生育期最重要气象特征变量,逐次添加空间特征变量和气象灾害特征变量,形成不同的模型输入特征变量组合。其次,应用GBDT算法建立模型估算苹果相对气象产量,以yw估算值和实测值之间的误差最小化为优化目标,获得最佳模型输入特征变量组合。然后,逐次添加苹果落叶休眠期、萌芽幼果期、果实膨大期、着色成熟期内的最佳模型输入变量组合,构建不同生育期的苹果相对气象产量预测模型,以模型测试集均方根误差(RMSE)最小化为依据,确定苹果相对气象产量预测的提前生育期。最后,逐次添加苹果生长季内各月份的最佳模型输入特征变量组合,构建苹果生长季内不同月份的苹果相对气象产量预测模型,以模型测试集归一化RMSE最小化为依据,确定苹果相对气象产量预测的提前月份。并且在不同生育期和生长季内不同月份的模型预测精度分析过程中,将相对气象产量转换为实际产量,比较其与以相对气象产量为目标变量的机器学习模型精度,从而判断苹果相对气象产量模拟模型构建方法精度。

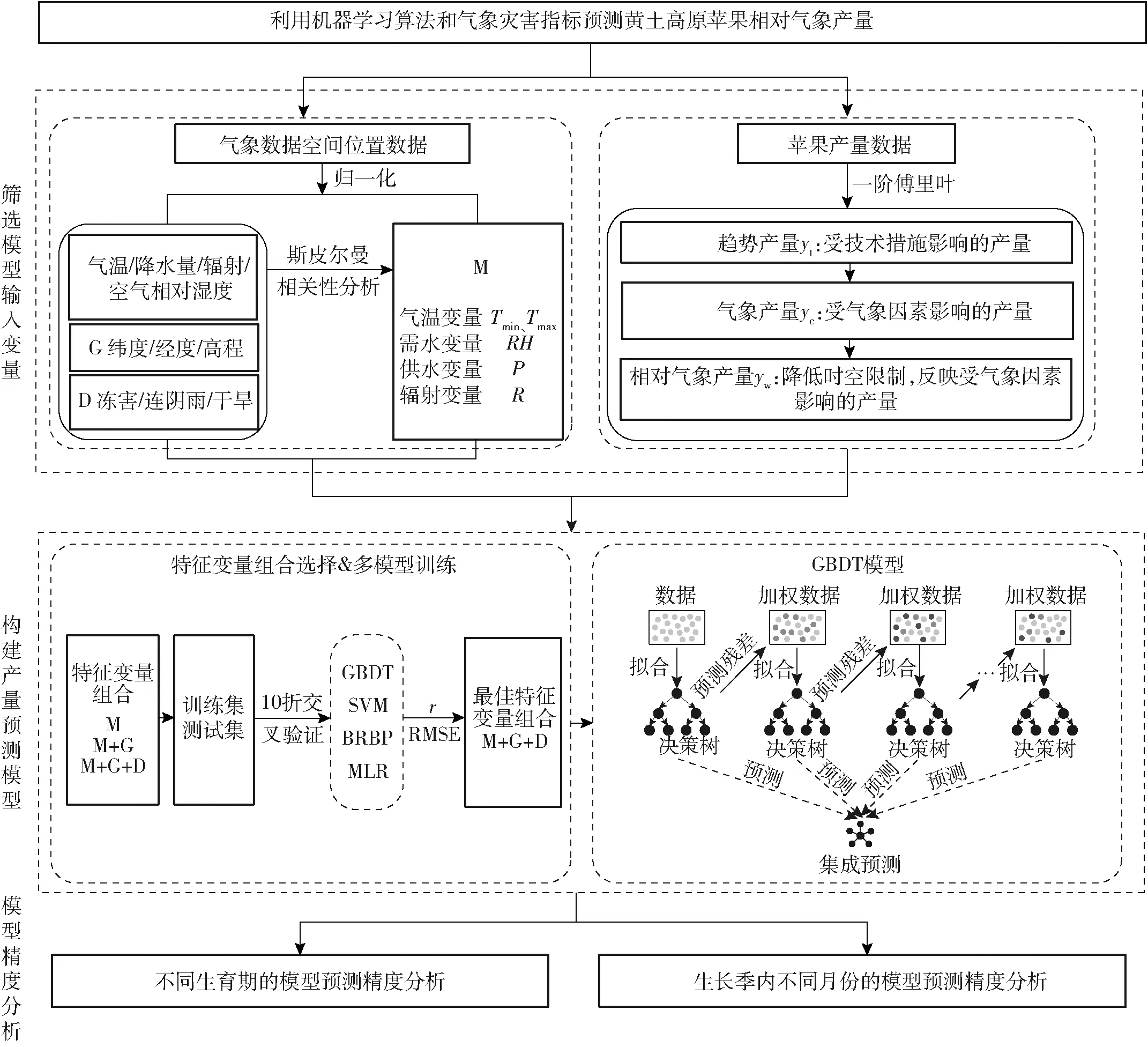
图2 苹果相对气象产量模拟模型流程图

模型模拟前,随机选取70%观测数据作为训练数据集,30%数据作为测试数据集,以10折交叉验证误差为原则对模型参数进行寻优。为降低模型精度极大值和极小值的影响,模型的最终精度为100次运行误差的50%分位数。

1.5 模型精度评价

采用皮尔逊相关系数(Pearson correlation coefficient,r)和均方根误差(Root mean square error,RMSE)2个统计指标来评价模型模拟精度。

2 结果与分析

2.1 影响苹果产量的气象特征变量

本文分析了目标变量(苹果相对气象产量)与气象特征变量之间的相关关系(图3,P<0.05),发现气温特征变量Tmean、Tmin、Tmax、Td、AT、NT与目标变量之间存在正相关关系,其中Tmax与目标变量的相关性最高(r=0.26)。为了避免输入因子间共线性对模型精度的影响,可同时选择与Tmax相关系数小于0.5的其他气温特征变量,其中符合要求的两个气温特征变量为Tmin与NT,但是它们之间存在较强的相关性,且Tmin与目标变量之间的相关性强于NT,因此最终只选择Tmax和Tmin作为模型输入的气温特征变量。需水特征变量RH与目标变量之间呈负相关关系,而供水特征变量P、辐射特征变量R与目标变量之间的相关性系数较小。因此,本文最终选取Tmax、Tmin、RH、P、R作为苹果相对气象产量模拟模型输入的最重要气象特征变量。

图3 目标变量(苹果相对气象产量)与气象特征变量关联热图

2.2 基于多种特征变量的不同苹果产量模型模拟精度分析

分别使用苹果整个生长季内的最重要气象特征变量组合(M),最重要气象特征变量和空间特征变量组合(M+G),以及最重要气象特征变量、空间特征变量和气象灾害特征变量组合(M+G+D)作为不同的模型输入特征变量组合,分别驱动基于GBDT、SVM、BRBP和MLR算法的苹果相对气象产量模拟模型,并比较不同模型测试数据集的模拟精度(图4,图中虚线表示1∶1线;**表示P<0.01)。当仅以最重要气象特征变量M作为模型输入变量特征组合时,SVM模型具有最大的r值(0.70),而BRBP模型的预测误差最小(RMSE为0.46)且数据点均匀分布在1∶1线的两侧(图4a、4d、4g、4j)。当以M+G作为模型输入特征变量集时,与仅以M作为模型输入特征变量的情形相比,GBDT和BRBP的RMSE分别降低2%、2.17%,同时GBDT、BRBP和MLR模型的r分别提升4.76%、2.99%和1.72%,但SVM模型的精度无变化(图4b、4e、4h、4k)。可见在模型输入气象特征变量中再加入空间特征变量,可以提高苹果相对气象产量模拟模型的预测精度。进一步在上述模型输入变量中再添加气象灾害特征变量(M+G+D),结果表明增加气象灾害特征变量可使GBDT、BRBP和MLR模型预测精度进一步提升,其中GBDT模型的模拟精度提升效果最为明显,其r增加16.67%,RMSE减少10.20%,而SVM模型的模拟精度则有所下降(图4c、4f、4i、4l)。

总体而言,基于GBDT和BRBP这2种机器学习算法和M+G+D输入特征变量组合建立的苹果相对气象产量预测模型,其模拟精度普遍优于MLR算法模拟。这可能是因为苹果相对气象产量与最重要气象特征变量、空间特征变量和气象灾害特征变量之间存在较强的非线性关系,而机器学习算法比多元线性回归方法更能准确描述这种非线性关系。因此,本文采用M+G+D组合作为最佳的模型输入特征变量组合。

2.3 模型模拟误差空间分析

以苹果整个生长季内的M+G+D特征变量组合作为模型输入变量,驱动基于不同算法建立的苹果相对气象产量模拟模型,可进一步分析不同模型在黄土高原各省份的总体模拟精度(图5,图中每个箱体包含各省苹果生产基地县的苹果相对气象产量模拟结果,箱体上、下限为数据的上四分位数和下四分位数,中间实线为数据中位数,箱体外的两条线为上边缘和下边缘,超出上下边缘的值为异常值)。由图5可知,不同模型在不同省份的表现存在较大差异,其中BRBP模型在河南省和陕西省表现最佳,SVM模型在山西省和甘肃省表现较佳。河南、山西、陕西和甘肃各省最佳模型的 RMSE均值分别为0.47、0.11、0.39和0.20。在这4个省份中,山西省的模型总体估计误差相对较小,4个模型的RMSE平均值仅为0.24,且误差分布相对较为集中。但河南省RMSE箱型图的箱体最长,这可能由于本文中河南省仅有3个苹果基地县,数据量较少使得箱型图的分布范围较大。

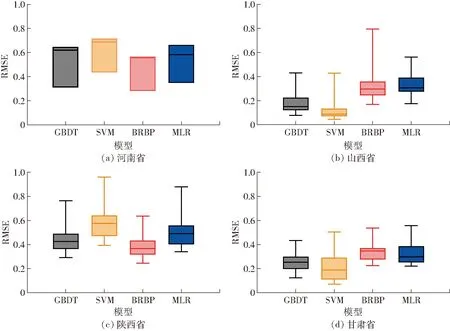
图5 基于最重要气象、空间和气象灾害特征变量组合和不同算法的模拟模型在4个不同省份模拟苹果相对气象产量的RMSE箱型图

2.4 苹果不同生育期输入特征变量组合对模型模拟精度的影响

进一步探究在M+G+D输入变量组合下,不同模型在不同生育期(落叶休眠期、萌芽幼果期、果实膨大期、着色成熟期)的苹果产量预测精度(图6)。当以相对气象产量作为目标变量时,对于GBDT和BRBP模型,各生育期模型的模拟精度无明显变化,其RMSE分别保持在0.44～0.46和0.44～0.45之间,这表明这2种模型在苹果各个生育期内均能获得相对较高的相对气象产量预测精度(图6a)。在不同苹果生育期,SVM模型的RMSE先减小后增加,次年8月产量预测的RMSE具有最低值(0.51),可见SVM模型可在果实膨大期获取最好的预测结果。MLR模型模拟的RMSE随着苹果生长发育的推进而逐渐减小,并在次年8月获得最佳的预测结果,与次年10月该模型的苹果相对气象产量预测精度仅相差0.01,表明该模型可在苹果果实膨大期就获取较为理想的苹果相对气象产量预测结果。当将相对气象产量转换为实际产量时,GBDT、BRBP、MLR模型在各生育期的模拟精度均呈现减小趋势(图6b)。具体而言,GBDT和BRBP模型在苹果各个生育期内均能获得相对较高的实际产量预测精度,其RMSE分别保持在4.42～4.90 kg/hm2和4.62～5.20 kg/hm2之间。MLR模型在果实膨大期的预测精度与着色成熟期仅相差0.03 kg/hm2,表明该模型在果实膨大期也能获取较为理想的苹果产量预测精度。SVM模型的RMSE先减小后增加,并且在果实膨大期获取最好的预测结果(5.04 kg/hm2)。

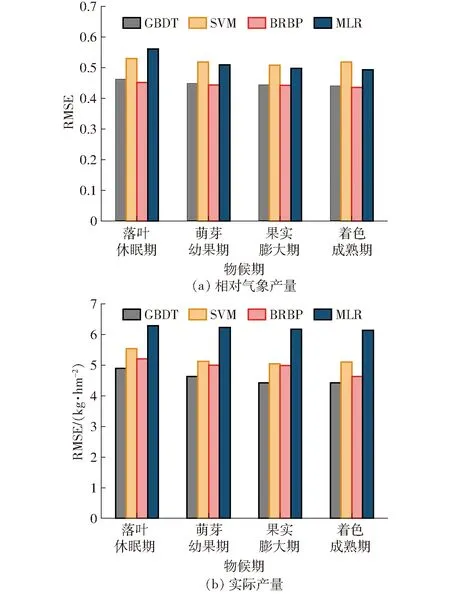
图6 基于GBDT、SVM、BRBP和MLR算法的不同模拟模型在苹果不同生育期模拟黄土高原苹果产量的精度对比

2.5 苹果生长季内不同月份的模型预测精度

在生长季内不同月份对苹果相对气象产量进行预测模拟并分析其精度,可确定出苹果产量预测的最佳提前期。根据生长季内不同月份各模型模拟结果归一化RMSE,可知4种模型的模拟精度都呈现出类似的变化趋势(图7a)。即随着苹果生育期的推进,模型输入变量不断增多,各模型的归一化RMSE逐渐减少。当以相对气象产量作为目标变量时,对于GBDT和BRBP算法,基于生长季内所有月份输入特征变量的结果最佳。与基于生长季所有月份输入变量的模型模拟结果归一化RMSE相比,在次年9月这2个模型的归一化RMSE分别与之仅相差0.62%和1.04%,精度非常相近。SVM算法可在次年8月获取最佳的预测精度。基于MLR算法的苹果相对气象产量预测模型可在次年9月获得最小的归一化RMSE。当将相对气象产量转换为实际产量时,GBDT和BRBP算法在次年9月的产量预测精度分别与次年10月仅相差0.38%和1.34%,而SVM和MLR算法分别在次年8月和次年9月模型预测精度最佳(图7b)。综上所述,本文建立的4种不同模型均可在苹果成熟期前1～2个月实现苹果相对气象产量的相对准确预测。

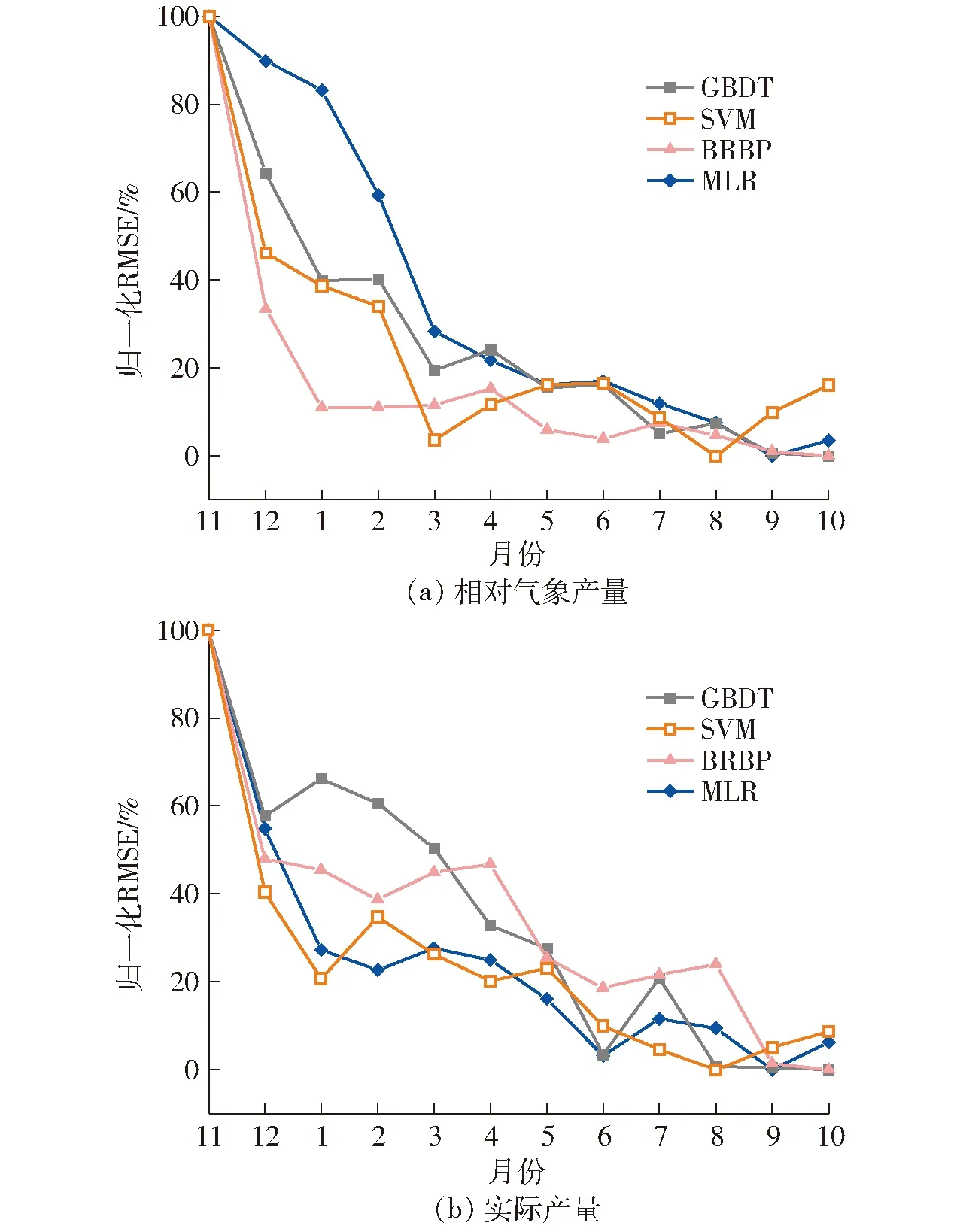
图7 基于GBDT、SVM、BRBP和MLR算法的不同模拟模型在苹果生长季内各月份模拟黄土高原苹果产量的归一化RMSE

3 讨论

3.1 影响苹果产量的特征变量和产量去趋势方法

气象要素和气象灾害对苹果产量具有重要的影响。本文选择了苹果产量形成过程中具有代表性的气象变量和气象灾害变量,包括Tmean、Tmin、Tmax、Td、AT、NT、RH、P、R、N4≤0℃、CR和SPEI。其次,气象特征变量筛选结果表明Tmin、Tmax、RH、P、R是影响黄土高原苹果相对气象产量预测模型的精度的重要气象特征变量,这与前人的研究结果相一致。白秀广等[31]和张强[32]研究表明,气温对苹果产量有正向影响,降水量、空气相对湿度和日照时数对苹果产量有负面影响。本文中降水量和太阳辐射与苹果相对气象产量之间的相关系数较小,这可能是因为黄土高原降水不均匀特征和灌溉等因素影响了降水量与苹果产量间的相关性[33]。此外,本文中苹果产量的样本量可能也影响了太阳辐射与苹果产量之间的相关性。随后,在最重要气象特征变量中依次加入空间特征变量和气象灾害特征变量,均可进一步提升基于GBDT、BRBP和MLR算法的苹果相对气象产量模拟模型的预测精度。当模型输入特征组合为“气象特征变量M+空间特征变量G+气象灾害特征变量D”时模型精度最高。刘峻明等[34]研究表明,气象站点空间位置会影响作物的积温和物候,但由于气候条件往往存在一定的年际变化,导致空间位置和气象要素的相关性较弱。所以,作物产量预测模型中需要同时考虑气象特征变量和空间特征变量。FENG等[35]研究发现,需要在作物产量预测模型中加入气象灾害,以此减少气象灾害给作物产量预测结果带来的不确定性。然而,本文中加入气象灾害特征变量会导致SVM模型的预测精度降低,这可能是因为该算法易受数据维度的影响,而气象灾害因子的加入增加了样本维度,从而导致模型性能受损[36]。

苹果相对气象产量仅受气象条件的影响,但是该产量不能通过测量直接获取,因此需对实际苹果产量数据进行预处理,而数据处理方法的选择就甚为重要。本文采用了一阶傅里叶对所有基地县的苹果单产去趋势得到苹果相对气象产量,这可以在一定程度上消除其他因素对产量的影响,从而能准确地反映苹果产量随气象因子的非线性变化。然而,产量去趋势其他方法还包括:线性回归、多项式回归、指数回归、对数回归、滑动平均、Logistic回归、HP滤波、局部加权回归等[37-40]。此外,由于社会、经济发展不平衡,不同区域的作物产量变化趋势也会存在差异性[41]。因此,在今后的研究中需要在各苹果生产县采用不同的去趋势方法获得更加准确、客观的苹果相对气象产量,从而提升模型的模拟精度。

3.2 基于机器学习算法的苹果相对气象产量模拟模型

机器学习模型能够较好地建立气象灾害因子与产量之间的关系,而这是作物模型普遍无法实现的[42]。在模拟黄土高原苹果相对气象产量的过程中,本文发现非线性算法GBDT、BRBP优于线性算法MLR。当以M+G+D组合作为模型输入特征变量组合来驱动本文所建立的模型模拟苹果相对气象产量时,机器学习模型(GBDT、BRBP模型)的r和RMSE分别比线性模型(MLR模型)高11.11%～22.22%和低10.20%,这表明模型输入特征变量与苹果相对气象产量之间存在较强的非线性关系,机器学习算法比线性算法能够更为准确地描述这种非线性关系。前人研究也发现气温、太阳辐射、降水量、空气相对湿度等气象要素、空间要素和气象灾害要素与苹果产量之间存在非线性关系[11,24,34,43-44],本文结果与这些结论基本相同。然而,基于SVM算法建立的苹果相对气象产量预测模型的RMSE均高于线性模型,这可能是因为输入变量之间存在较强的线性关系,破坏了SVM模型的预测性能,从而导致SVM模型预测结果与线性模型相近甚至更差[45]。此外,本文还探究了在苹果生长季内不同月份各模型预测苹果相对气象产量的精度。结果表明,当以M+G+D特征变量组合作为模型输入变量时,本文建立的4种模型均可在果实成熟前的1～2个月获得较高精度的苹果相对气象产量预测结果。本文所构建的苹果相对气象产量模拟模型在苹果生长季内不同月份的预测中模拟精度存在差异,这一方面可能因为不同月份气象特征变量对苹果产量的影响并非同等重要[13]。另一方面可能是由于特征变量的输入个数随着月份的递增而增加,机器学习模型对更多数量的输入特征通常模拟精度可能更佳。已有研究表明小麦、玉米、水稻等粮食作物均可在收获前的1～2个月实现较为准确的早期产量预测,这些结果也与本文的结果较为一致[21,46]。并且将相对气象产量转换为实际产量后,4种模型在苹果生长季内不同月份的模拟精度变化趋势基本一致,仅在数值上存在部分差异,可能是苹果实际产量受到技术措施等其他因素影响所导致的。这表明本文所构建的苹果产量模型具有较好的预测精度。

3.3 气象特征变量和气象灾害特征变量对苹果相对气象产量模拟精度的影响

本文通过筛选,最终确定了预测苹果相对气象产量的输入特征变量为:气象特征变量Tmax、Tmin、RH、P、R,气象灾害特征变量N4≤0℃、CR、SPEI,空间特征变量Lat、Lon、Ele。以机器学习模型(GBDT、SVM、BRBP、MLR模型)在苹果生长季内不同月份的表现来看,空间特征变量在模型输入中是固定不变的,但是随着苹果生育期从冬季休眠期(本年11月)发展到收获期(次年10月),输入模型的最重要气象特征变量和气象灾害特征变量的时间序列逐渐递增,而此过程中所有模型的RMSE均逐渐减小(图7)。这表明气象特征变量和气象灾害特征变量在模型性能的后续提升过程中发挥着关键作用。因此,相比于空间特征变量,气象特征变量和气象灾害特征变量对苹果相对气象产量模拟模型精度的影响更大。

3.4 苹果相对气象产量模拟模型的不足

本文建立的黄土高原苹果相对气象产量预测模型也存在一定的不足。首先,本文所建立模型的输入数据较为单一,然而苹果的生长发育过程非常复杂,产量形成过程中受到众多因素的影响,例如土壤[40,47]、灌溉、施肥以及园艺管理措施[48]等。因此,在未来的研究中应考虑将上述因子纳入模型的输入特征变量组合,这将会进一步提高苹果相对气象产量模型的模拟精度。其次,本文选用的3种机器学习算法均为黑箱模型,并不能定量化解释输入变量对目标变量的影响[49-50]。最后,本文还未能将所选的最佳预测模型在其他不同苹果种植区域和不同的气候环境下进行充分验证。例如,LI等[11]建立了陕西省县域产量预测模型,并预测了未来气候条件下28个苹果基地县的产量。因此,在随后的研究中拟将本文建立的苹果相对气象产量预测模型推广至整个黄土高原的苹果种植适宜区,并利用其分析未来气候变化条件下黄土高原产区的苹果相对气象产量变化。