基于变环量设计的混流泵叶轮多工况优化

王梦成 焦海峰 周正富 袁建平 夏鹤鹏 陈松山

(1.扬州大学电气与能源动力工程学院,扬州 225127; 2.江苏大学国家水泵研究中心,镇江 212013;3.江苏省水利工程科技咨询股份有限公司,南京 210029)

0 引言

混流泵由于其良好的综合性能,被广泛应用于日常生产生活等领域。然而,由于外部运行条件的复杂性,其常于偏工况下运行,因此,研究其多工况优化以扩大其高效区范围对降低能源消耗具有重要意义[1]。相比于采用几何参数作为设计参数的传统设计,使用水动力参数作为设计参数的环量法具有参数与水力性能联系紧密[2]以及叶片角分布更加多样[3]等优点,其有效性已在水泵、水轮机、风机、压缩机和喷水推进器等[4-10]领域的设计优化中得到广泛证明。

在众多有关环量法的研究中,文献[11-13]指出,轮毂及轮缘处环量沿轴面流线方向的偏导数 (载荷) 为环量法的核心,其分布形式与流场及叶片形状直接相关;文献[14-16]指出,在环量法中,通过控制叶片尾缘倾角,有利于混流泵叶轮内部二次流与流动分离现象的抑制。因此,在过往的大多数基于环量法的优化研究中,仅载荷与叶片尾缘倾角被作为设计参数,而叶轮出口翼展方向环量则被设为恒定值以便于叶轮理论扬程的控制。尽管上述研究也获得了较好的效果,但由于叶轮出口翼展方向环量分布形式对混流泵性能的影响在优化过程中未被考虑,因此,优化结果仅为部分(轮毂及轮缘处)环量的最佳组合。

由环量法控制方程组[17]可知,叶轮出口环量分布与流线方向载荷分布密切相关,且相关研究[18]表明,相比于叶轮出口环量恒定分布,存在更加适合的变环量分布形式。目前,在基于环量法的优化研究中,关于叶轮出口环量分布对混流泵性能影响的研究仍较少。文献[19]研究了3种线性环量分布对混流泵效率及空化性能的影响;本课题组在前人工作的基础上通过插入控制点并微调总环量的方法,在保持扬程变化小于3%的基础上研究了17种非线性环量分布对混流泵叶轮效率及空化性能的影响,并通过单目标优化量化了该影响的数值[20-21];文献[22-23]在混流式泵喷的优化研究中通过试错法研究了叶轮出口环量线性分布对泵喷性能的影响。然而上述研究均存在着各自的局限性,如文献[19-20]忽略了叶轮出口环量分布与流线方向载荷分布的联系;文献[22-23]则需要人为给出每种环量分布,通过反复的试错过程确定最终解。

本文以环量法为基础,以叶轮出口环量分布控制参数、流线方向载荷和叶片尾缘倾角为设计参数,以设计点扬程变化小于3%为约束条件,以0.8、1.2倍设计流量点处效率为优化目标,结合实验设计、近似模型和优化算法,对混流泵叶轮进行多工况优化研究,以期最大化拓宽其高效区范围。

1 环量法

1.1 理论基础

在本研究中,混流泵叶片的参数化由三维反设计软件Turbodesign完成,其详细理论基础见文献[24],本文在此不再赘述,仅对其中的核心控制方程进行简要描述。在该方法中,流体被视为无粘理想流体,流体的粘性效应由阻塞因子来表达,流动为定常均匀流,流场中唯一涡量来源于叶片表面束缚涡量。在旋转坐标系下,相对速度可被分解为周向平均速度与周期脉动速度分别进行求解。其中周向平均速度符合流函数方程

(1)

式中φ——流函数

Bf——叶片阻塞因子

z——圆柱坐标系轴向坐标

r——圆柱坐标系径向坐标

f——包角,(°)

周期脉动速度符合势函数方程

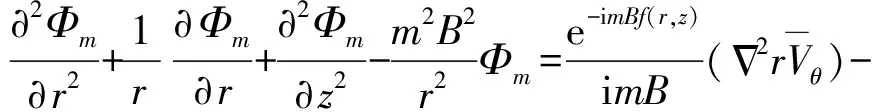
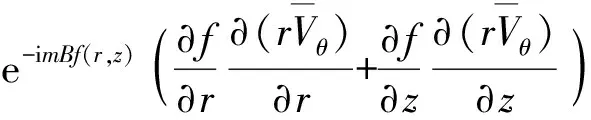
(2)

式中B——叶片数

m——傅里叶展开项数

Φm——势函数

叶片形状由流切条件进行计算,即

(3)

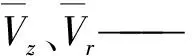
vzbl、vrbl、vθbl——周期脉动速度的轴向、径向、周向分量,m/s

ω——叶轮旋转角速度,rad/s

式(1)～(3)共同构成环量法控制方程组,在此基础上,通过给定边界条件,即可根据如图1所示计算流程通过迭代计算得到相应叶片形状及流场分布,图中n表示迭代次数。

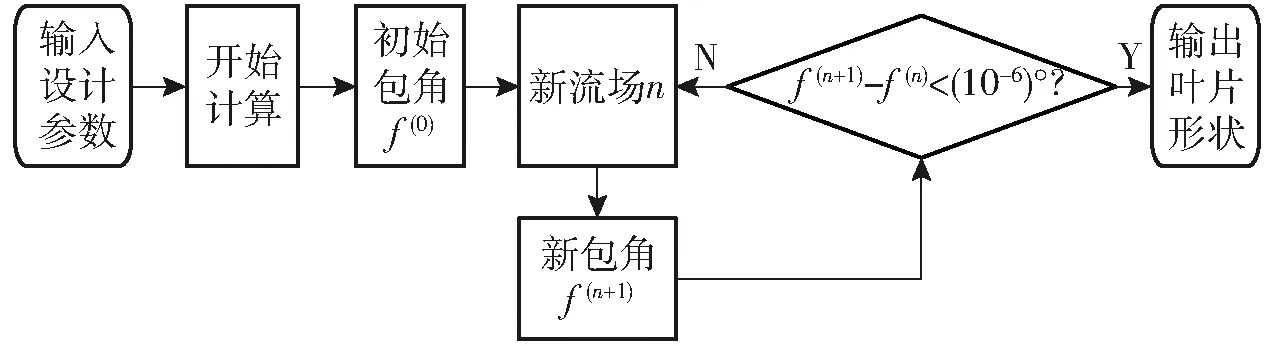
图1 环量法设计流程

1.2 设计参数

以一比转数为511的导叶式混流泵作为原始模型,其叶轮设计参数如表1所示。

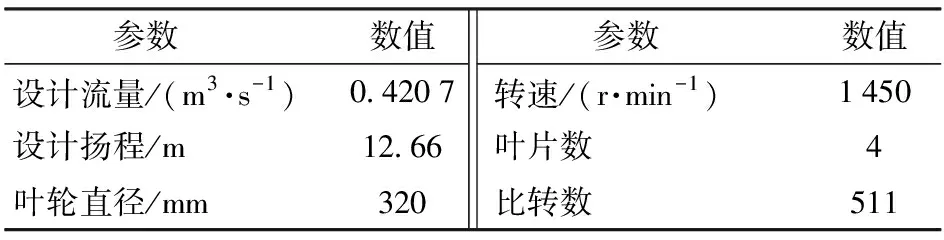
表1 原始模型设计参数

在环量法中,当叶轮设计参数确定后,输入参数包括轴面投影图、叶片厚度分布、流体属性、叶轮进口和出口处沿翼展方向环量分布、轮毂和轮缘处沿轴面流线方向载荷分布及叶片尾缘处倾角。本文选择环量、载荷及叶片倾角作为设计变量,其它参数均保持与原始模型一致且在优化过程中不对其进行任何更改。

在本研究中,叶轮进口处环量被设为零以满足叶轮进口处流动无预旋这一假设,而叶轮出口处环量分布则采用变环量控制以便于其在优化过程中能被实时调节。目前,主流的变环量控制方式有线性变化和非线性变化两种,前者如文献[19],后者如文献[20]。相比于前者,后者有更大的可能获得更加理想的结果,但控制方式过于复杂,存在引入控制参数过多且需要对每种环量分布进行人工调节的问题,进而导致优化过程需要消耗大量的时间且最终结果依赖于设计人员的经验。因此,本文采用文献[19]所述线性环量控制法,其分布形式如图2所示,则控制参数为斜率Kr,图中纵坐标表示由rsVs(叶轮出口轮缘处环量,rs表示叶轮出口轮缘处半径,Vs表示叶轮出口轮缘处切向速度)做无量纲处理后的环量;横坐标表示叶轮出口处轮毂到轮缘的归一化长度,其中0表示轮毂。

轮缘及轮毂处沿流线方向载荷分布采用如图3所示分段曲线来控制,叶片其余位置处载荷则由线性插值来确定。由图3可知,轮毂及轮缘处载荷分别由控制参数LE、NC、K和ND共同确定。其中,LE为叶片前缘处载荷;NC和ND分别表示第一段抛物线与中间直线交点、中间直线与最后一段抛物线交点在流线方向的相对位置,K为中间直线斜率;纵坐标表示由rsVs做无量纲处理后的载荷;横坐标表示从叶片前缘到尾缘的归一化长度,0表示叶片前缘。

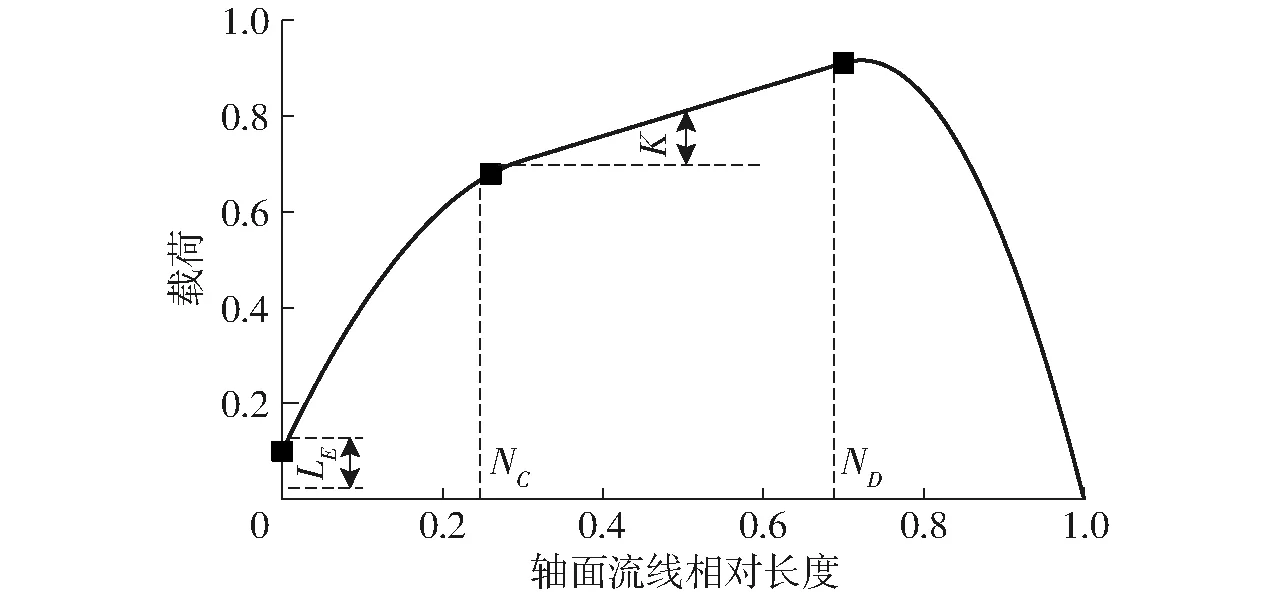
图3 流线方向载荷分布

考虑到叶片尾缘倾角β对叶轮内部二次流的抑制作用,其在本次研究中也被选为设计参数。因此,本文设计参数共10个。由于LE过大可能会引起叶片前缘过于扭曲,进而使得环量法计算发散导致叶片造型失败,轮毂及轮缘处LE选定为-0.2～0.2;为避免负加载这一不利现象在叶片造型中出现,轮毂及轮缘处K值不宜过大,故其范围选定为-2～2;轮毂及轮缘处NC和ND的范围则根据课题组先前设计经验选定,最终结果如表2所示,表中下标s和h分别表示轮缘及轮毂。

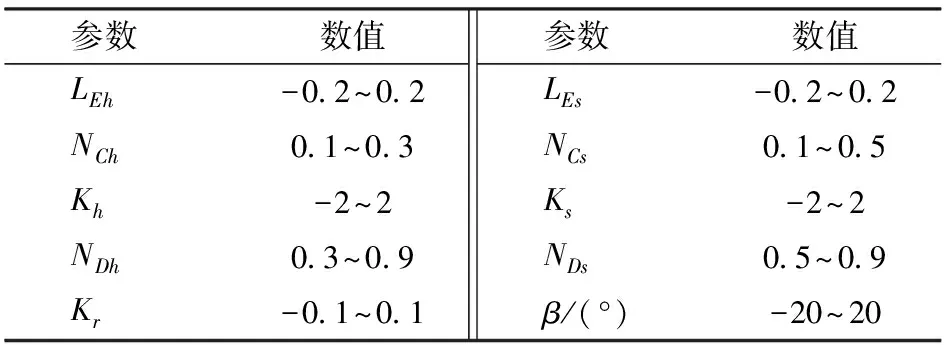
表2 设计参数

1.3 有效性验证

由不可压缩势流理论[25]可知

(4)

式中ρ——流体密度,kg/m3

Wmbl——叶片表面相对流速平均值,m/s

p+、p-——叶片工作面、背面处静压,Pa

由式(4)可知,在环量法中,环量分布与叶片表面压力分布直接相关。因此,本文采用文献[26]所述方法对环量法的有效性进行验证。首先,在环量法中采用图4所示载荷分布[18]对一混流泵叶轮进行水力设计;然后,在设计工况下,采用数值模拟对叶片表面压力分布进行计算;最后将数值模拟所得压力分布与环量法输出压力分布进行对比,结果如图5所示。由图5可知,两者具有较好的一致性,静压最大差值出现于叶片前缘和尾缘处。考虑到环量法中流体无粘假设及叶片厚度为零的假设,而在数值模拟中,流体的粘性及叶片厚度均被纳入计算过程,因此,可以认为前缘及尾缘处误差在可接受范围内,故采用环量法对混流泵叶轮进行设计优化是可行的。

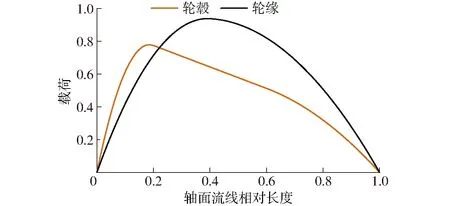
图4 载荷分布

2 数值模拟及准确性验证

数值模拟的准确性对本文研究结果的可靠性具有重要影响。因此,本节将对数值模拟方法进行简要描述并采用实验对其准确性进行验证。

2.1 计算设置

在本研究中,数值模拟的求解采用CFX完成。湍流模型选用可有效预测混流泵内部流动分离现象的SSTk-ω模型;壁面函数采用“Automatic”;对流项求解选用“High Resolution”;泵段进口设为“Mass Flow Rate”,泵段出口设为“Opening”以允许回流的产生,使其符合实际流动;叶轮与进水管和导叶之间的交界面采用“FrozenRotor”,导叶与出水管之间的交界面采用“None”;所有壁面处均采用“NoSlipWall”;为节约计算资源,在样本点计算中收敛精度设为5×10-5,结果验证及内流场分析时收敛精度设为1×10-5。

2.2 网格剖分

计算域离散是数值模拟的基础,因此,网格质量和数量均对计算结果的可靠性具有极大影响。为使计算过程易于收敛,计算结果更加精确,本文采用六面体结构化网格对进水直管、叶轮、导叶和出水弯管进行网格划分,并对上述4部件中所有近壁面处网格进行加密处理,结果如图6所示。

为排除网格数对计算结果的不利影响,以泵段设计点处效率作为检测目标对计算域内网格进行无关性检测,结果如图7所示。由图7可知,效率先随网格数的增大而增大,直至网格数到达4.71×106,随后基本不随网格数的增加而变化。因此,本研究以网格数4.71×106作为网格划分最终方案,此时,进水直管、叶轮、导叶和出水弯管的网格数分别为8.3×105、1.41×106、1.52×106和9.5×105。

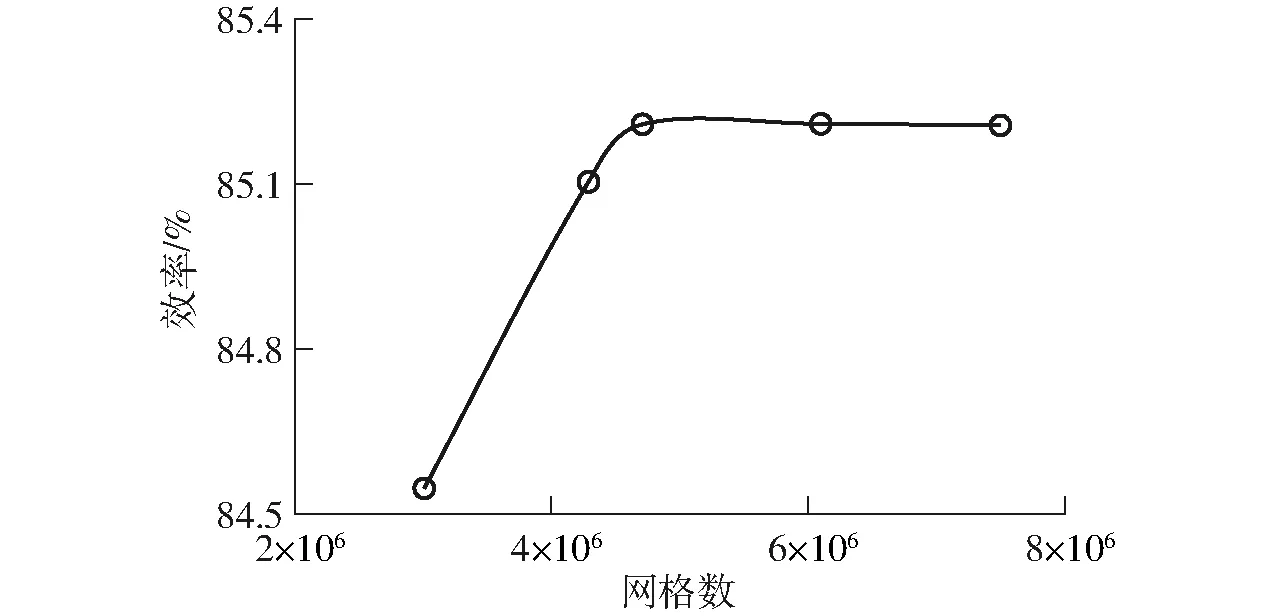
图7 网格无关性测试结果

2.3 实验验证

采用上述计算设置和网格划分对原始模型I0进行数值模拟,并分别对效率及扬程进行计算,然后将模拟值和实验值分别进行对比,对比结果如图8所示,其中实验在如图9所示的综合不确定度在±0.28%范围内的江苏大学国家水泵中心水力四象限多功能实验台上完成。由图8可知,实验值和模拟值具有较好的一致性,两者最大误差不超过2.5%,且最大误差出现在小流量处。因此,可以认为,数值模拟的准确性足以保证本研究的可靠性。

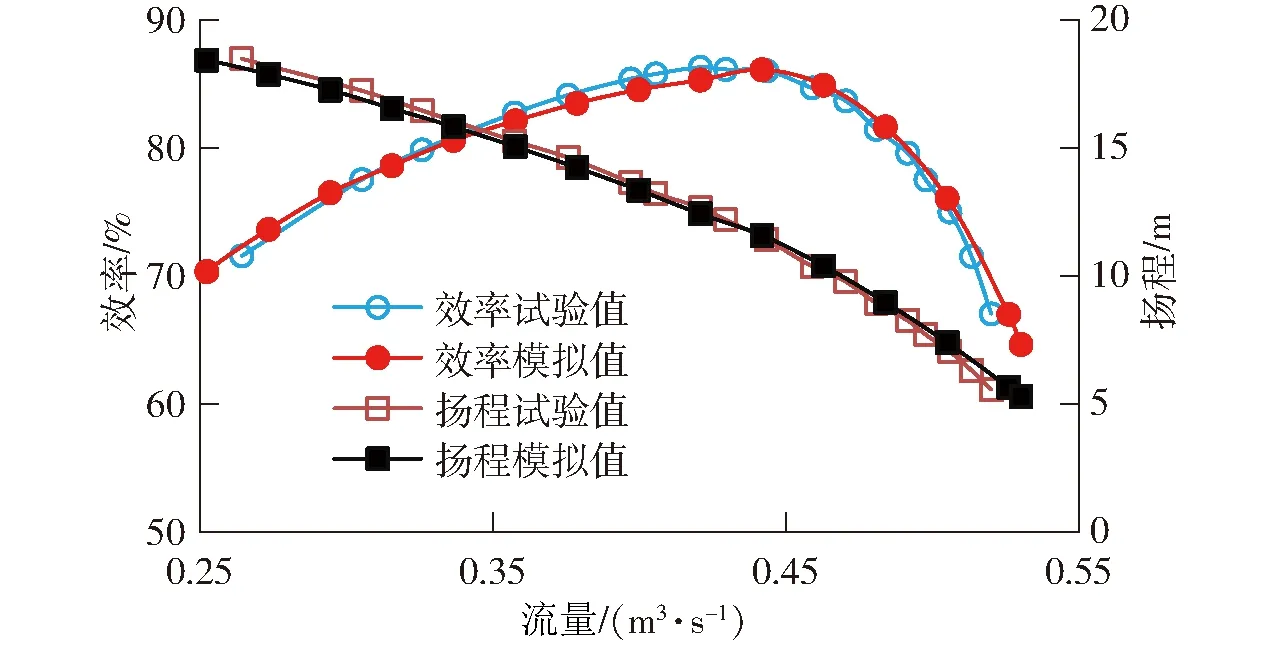
图8 模拟验证

图9 实验测量

图8中扬程及效率计算公式为

(5)

(6)

式中Pout——出口处总压,Pa

Pin——进口处总压,Pa

Q——流量,m3/s

M——力矩,N·m

g——重力加速度,m/s2

H——扬程,m

η——效率,%

3 优化方法

3.1 优化目标及约束条件

由图8可知,原始模型在设计工况处具有较好的水力性能,然而,随着流量逐渐偏离设计工况,效率迅速下降,特别是在大流量工况下。根据统计分析[18],由于外部条件的影响,该类水泵常运行于0.8～1.2倍设计流量之间,为使优化后混流泵模型具有更为优秀的水力性能及相似比转数,本文以该水泵在0.8、1.2倍设计点处的效率η0.8和η1.2为优化目标,以设计点扬程H1.0变化小于3%为约束条件,对该混流泵模型进行设计优化。

3.2 优化流程

优化流程如图10所示,图中红色线框表示数值模拟,采用第2节所述网格划分及计算设置;蓝色线框表示优化过程中涉及到的各种算法,具体设置如下文所述。

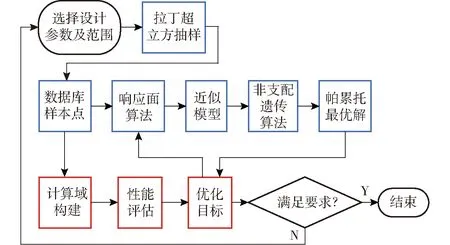
图10 设计优化流程图

样本点的生成由最优拉丁超立方抽样法[27]完成,在本研究中,共计生成了110个不同的样本点。由于设计参数包含叶轮出口环量控制参数,因此,为防止样本模型扬程出现过大波动,进而影响所构建的近似模型的扬程预测精度,需要对扬程波动较大的样本点(偏离设计扬程超过10%)进行剔除并额外增加相应的样本点。各样本点扬程变化如图11所示,蓝色点和红色点分别表示扬程满足要求和不满足要求的样本点。由图11可知,仅需对编号为2和37的两个样本点进行替换。

通过构建设计参数与优化目标间的近似模型,可以避免寻优过程中数值模拟的重复调用,从而加快寻优进程。由于响应面算法[28]具有数学理论充足、应用范围广及实用性强等优点,因此,本文采用二阶响应面模型分别构建设计参数与优化目标及约束条件间的映射关系,其表达式为

(7)

式中yk——优化目标及约束条件

xi、xj——设计参数

N——设计参数个数

α0、αi、αii、αij——待定系数,其值由最小二乘法确定

多目标优化由非支配排序遗传算法[29]完成,该算法的主要思想为对种群中的个体按帕累托值进行排序,并按照排序值从小到大选择个体来解决多目标问题。在本研究中,初始种群数及最大遗传代数分别设为200和120,交叉及变异概率分别设为0.7和0.05。因此,共计生成了24 000种不同配置叶轮。

3.3 优化结果

优化结果如图12所示。由图可知,η1.2随着η0.8的增大而减小,因此,图12所示帕累托解集中所有解均具有相同优先级。根据I1(Maxη1.2,η0.8>η0.8ori)、I2(η1.2>η1.2ori,Maxη0.8)、I3((I1+I2)/2)这3种不同叶轮配置I1、I2和I3被选出做进一步研究。其中η0.8ori表示原始模型在0.8倍设计流量处效率;η1.2ori表示原始模型在1.2倍设计流量处效率。

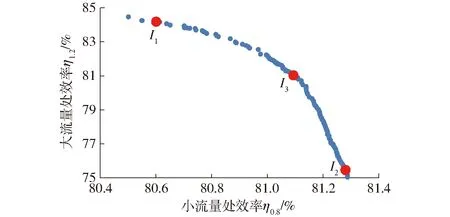
图12 优化结果

叶轮I1、I2和I3的设计参数如表3所示,由表3可知各设计参数均未达到所给参数范围的极限,因此,参数范围的选择是合理的。此外,叶轮I1、I2和I3中,Kh均为负值,而Ks和Kr均为正值,这意味着轮毂处流线方向载荷前加载,轮缘处流线方向载荷后加载,叶轮出口处翼展方向环量从轮毂到轮缘递增分布,均有利于混流泵性能的提升。

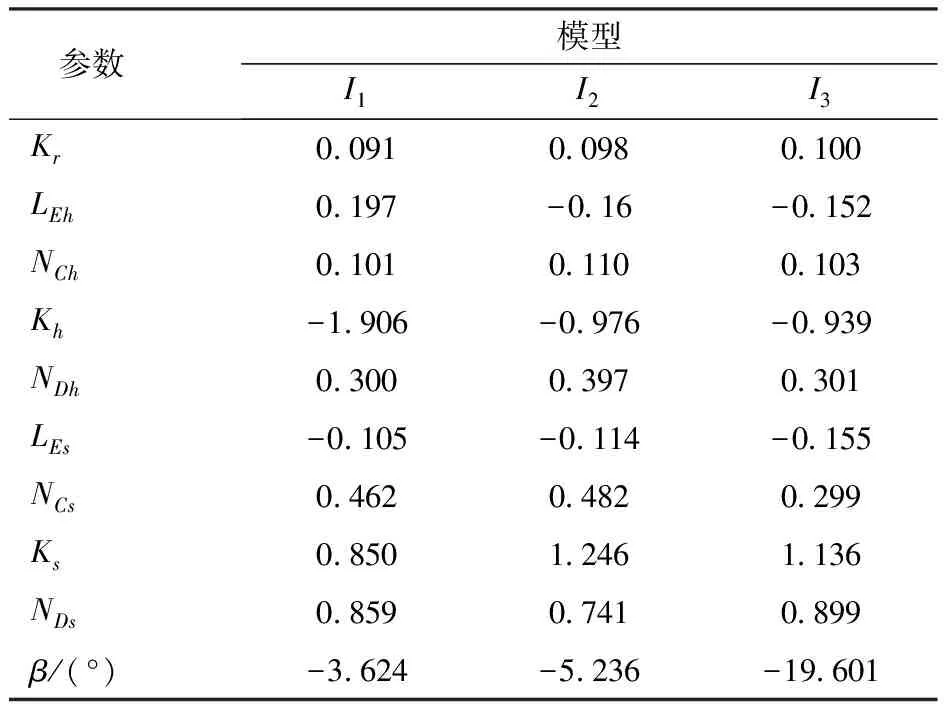
表3 优化后模型设计参数

叶轮I1、I2和I3的近似模型预测性能与数值模拟计算性能对比如表4所示。由表4可知,近似模型预测值与数值模拟计算值相差较小,因此,近似模型具有足够的预测精度。综合考虑优化后叶轮在0.8、1.2倍设计流量处效率的提升及其在设计点处扬程和效率的变化,叶轮I3被选为优选模型进行进一步分析。优选模型I3与原始模型I0叶片外形对比结果如图13所示,两者在叶片中后部出现了较大区别。

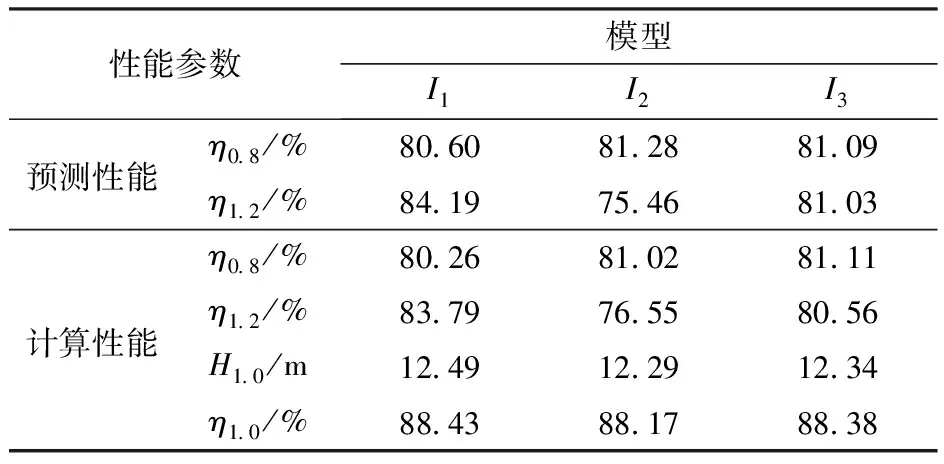
表4 近似模型预测与数值模拟计算对比

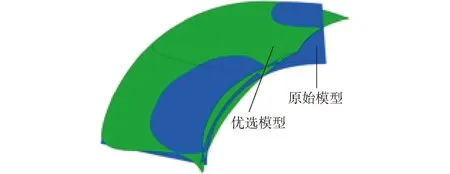
图13 原始模型与优选模型叶片外形对比

3.4 参数分析

为评估各设计参数与优化目标间的响应关系,采用敏感性分析[30]对计算结果进行处理,结果如图14所示。图中红色表示正面影响,蓝色表示负面影响。

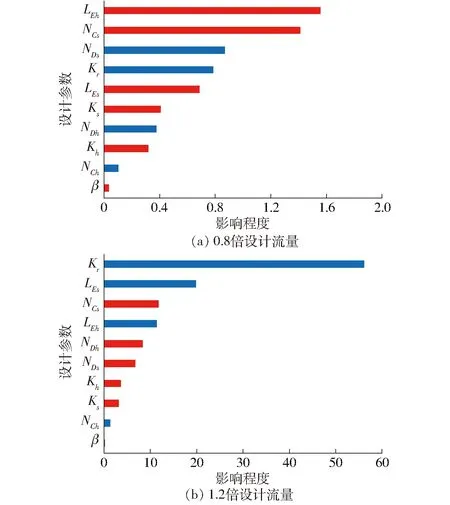
图14 不同工况敏感性分析

由图14可知,除参数NCh外,优化目标η0.8和η1.2对所有参数均具有竞争关系,这与图12所呈现的结果相一致。对η0.8影响最大的4个设计参数依次为LEh、NCs、NDs和Kr,影响最小的参数为β;对η1.2影响最大的4个参数依次为Kr、LEs、NCs和LEh,影响最小的参数也为β。因此,参数Kr对η0.8和η1.2均具有较大影响,而参数β对叶轮性能的影响则几乎可以被忽略,这与文献[14-16]的结果相反。造成该差异的原因主要是由于上述文献在优化过程中均未考虑叶轮出口环量分布对叶轮性能的影响,进而导致参数β通过控制叶片尾缘倾角影响叶片不同叶高处做功能力,从而造成了较大影响。然而,在本研究中,参数Kr通过控制叶轮出口环量分布直接控制叶片不同叶高处做功能力,从而抑制了参数β的作用。综上所述,在基于环量法的混流泵的多工况优化设计中,采用考虑叶轮出口环量分布的变环量设计是必要的,且在该方法中,各参数与混流泵性能之间的响应关系将与之前研究产生较大区别。

4 结果与分析

优选模型I3与原始模型I0的能量特性对比如图15所示。由图15可知,优选模型在0.8、1.0、1.2倍设计流量处效率分别为81.11%、88.38%和80.56%,相比于原始模型,效率分别提升0.63、3.18、6.72个百分点。优选模型在设计工况处扬程为12.33 m,与原始模型相比,扬程波动小于2%;在小流量工况,优选模型扬程小于原始模型,且流量越小,扬程差越大,最大扬程差约为3.8%;在大流量工况,两者扬程变化规律与小流量工况相反。因此,优选模型I3在保持设计点扬程变化较小的同时有效拓宽了其高效区范围,满足设计优化要求。

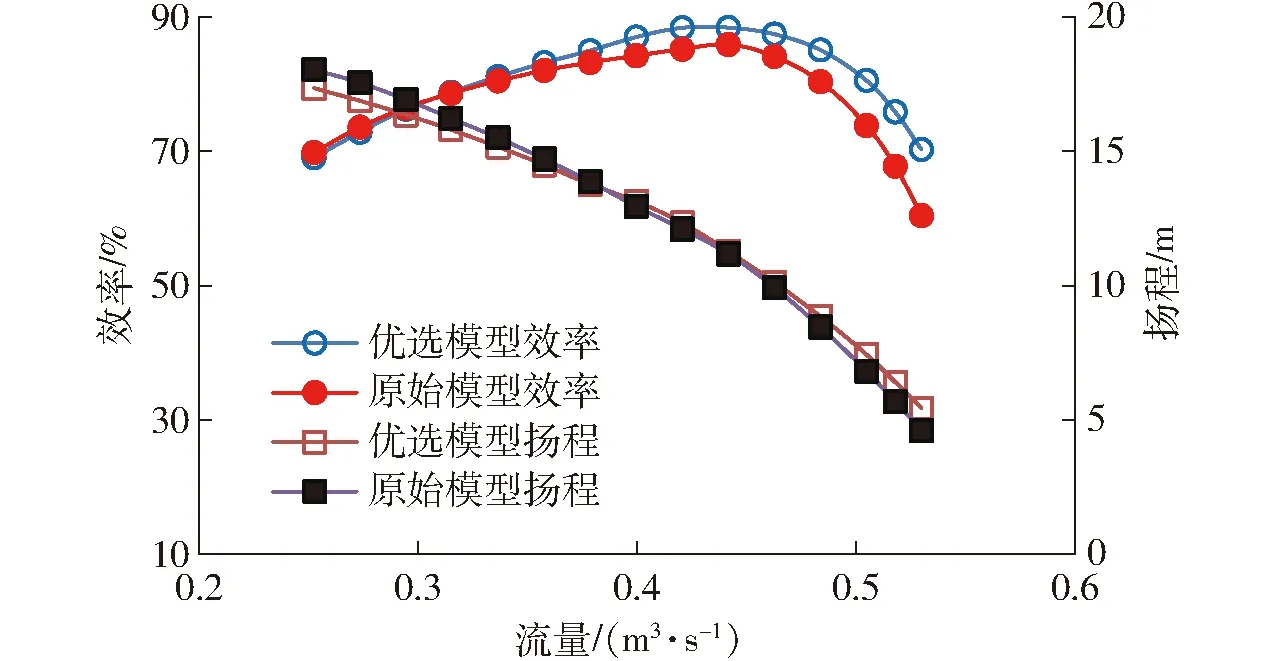
图15 外特性对比

为阐明优化机理,探究效率提升的根本原因,有必要对叶轮内部流态进行对比分析。考虑到壁面对流场的影响,取叶轮0.1、0.5、0.9倍翼展处压力分布进行对比,结果如图16所示。由图16可知,在0.5、0.9倍翼展处,原始模型内压力分布曲线较为扭曲,表明其内部存在着明显的压力畸变现象。相比于原始模型,优选模型内的压力分布更为光顺,这意味着其内部流态更加平稳。

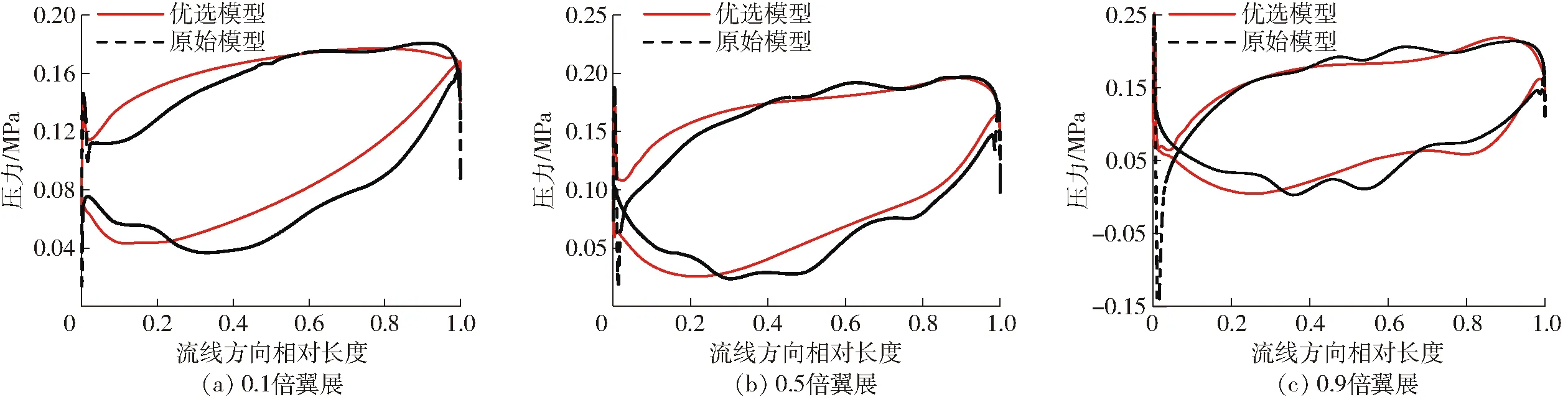
图16 不同跨度处流线方向压力分布

为进一步证明该观点,取不同翼展处周向展开图流场分布进行对比,结果如图17所示。由图17a可知,小流量工况下原始叶轮跨中处相对速度分布较为均匀,而轮毂侧叶片工作面出现了明显的低速区,轮缘侧叶片背面则出现了明显的高速区;在优选模型中,跨中处相对速度分布相较于原始叶轮更加均匀,然而轮毂侧叶片工作面低速区与轮缘侧叶片背面高速区几乎没有任何改善,这是优选模型在小流量工况处效率提升较小的根本原因。而在图17b中,大流量工况下优选模型在全流道范围内流速分布均比原始模型更加均匀,特别是在轮缘侧,叶片前缘工作面处由于入流角和叶片安放角不匹配所导致的低速回流区几乎被完全消除。

叶轮出口处翼展方向压力分布可在一定程度上反映叶片不同叶高处做功能力。原始模型与优选模型不同流量下叶轮出口处翼展方向压力分布对比如图18所示。由图18可知,相比于原始模型,优选模型在整个叶轮出口处叶高范围内做功能力分布更加均匀,这有助于叶轮下游部件中流体混合损失的减小,从而提升其能量特性。

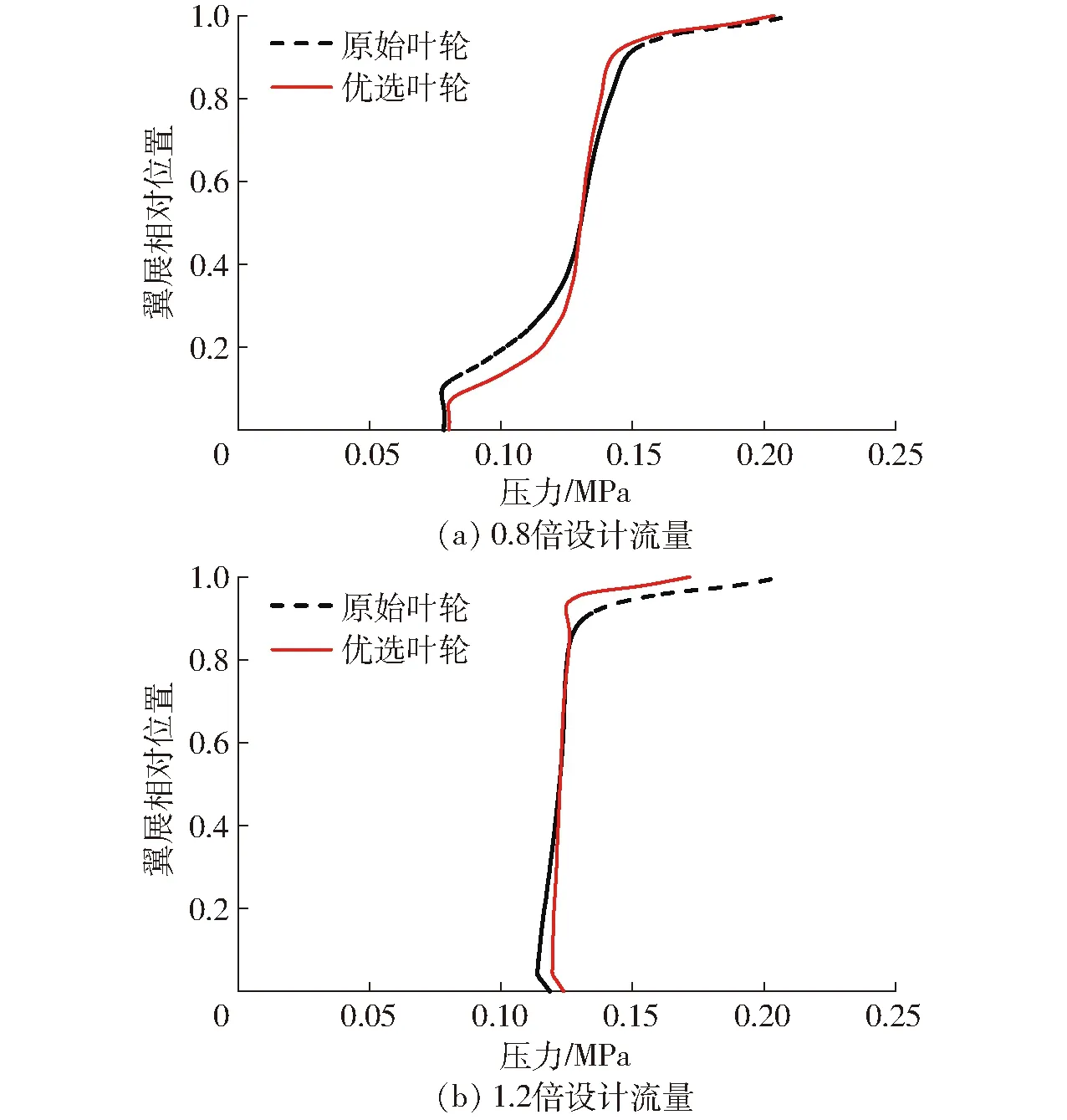
图18 叶轮出口处翼展方向压力分布对比

5 结论

(1)在变环量设计下,所有样本点中仅2个样本点扬程不满足要求,需要被替换。因此,采用变环量设计对混流泵叶轮进行设计优化是可行的。

(2)局部敏感性分析结果表明,叶轮出口环量控制参数Kr对大流量工况和小流量工况混流泵性能均具有极大影响,且其对叶片尾缘倾角与混流泵性能之间的响应关系也具有极大的影响。因此,在混流泵的多工况设计优化中采用变环量设计是必要的。

(3)优选模型I3在0.8、1.0、1.2倍设计流量处效率分别为81.11%、88.38%和80.56%,在设计流量处扬程为12.33 m,相比于原始模型,效率分别提升0.63、3.18、6.72个百分点,扬程波动小于2%。内流分析表明,优选模型内更为均匀的流场分布及叶轮出口处更加合理的做功能力分布是其性能提升的根本原因。